Среде
Плотность замедления
Плотность замедления q ( E ) представляет собой число нейтронов в единице объема, энергия которых изменяется за единицу времени от значения выше Е до некоторой энергии ниже Е.
Эта функция характеризует скорость, с которой нейтроны, замедляясь, пересекают некоторую данную энергию Е. Можно представить себе функцию q по аналогии с потоком жидкости как скорость потока нейтронов, движущихся по энергетической шкале. Плотность замедления имеет одно и то же значение в любой шкале, если измерения производятся при соответствующих друг другу величинах Е, ν или и, т.е. q ( E )= q ( v )= q ( u ).
Рассмотрим бесконечную среду без поглощения нейтронов, в которую непрерывно и равномерно по всему пространству вводятся нейтроны с энергией E0 со скоростью S 0 нейтронов в единицу времени и в единицу объема. В этой среде устанавливается стационарное состояние и число нейтронов в любом данном энергетическом интервале ∆Е и данном объеме будет постоянным во времени. Все нейтроны, вводимые в среду с энергией E0, замедляются до некоторой энергии ниже Е, поэтому q ( E 0 )= S 0 .
В стационарном состоянии число нейтронов, попадающих при замедлении в данный интервал энергии, должно быть при отсутствии поглощения равно числу нейтронов, покидающих при замедлении этот интервал, то есть нейтроны не накапливаются ни при какой энергии и ни в какой промежуток времени. Таким образом, для E < E 0 :
q ( E + dE )= q ( E ) или 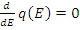 и q ( E )= const
и q ( E )= const
Если использовать начальное условие, то q ( E )= S 0 . Следовательно, плотность замедления, по этой модели, не зависит от энергии.
Определим соотношение между плотностью потока и плотностью замедления. R ( u ) du = ΣS ( u )Ф( u ) du - полное число рассеяний нейтронов, энергии которых кат в интервале du около и, отнесенных к единице объема и единице времени.
Эту же величину можно также получить с помощью плотности замедления q(u), т.е. R ( u ) du = q ( u ) 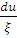 , где — есть среднее число рассеяний, выводящих нейтроны из интервала du . Приравняв эти выражения, получим q ( u )=ξΣ S ( u )Ф( u ) ( в случае бесконечной чисто рассеивающей среды).
, где — есть среднее число рассеяний, выводящих нейтроны из интервала du . Приравняв эти выражения, получим q ( u )=ξΣ S ( u )Ф( u ) ( в случае бесконечной чисто рассеивающей среды).
С учетом Ф(Е)dE=-Ф(u)du, 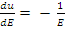 получим q ( E )= ξEES ( E )Ф( E ).
получим q ( E )= ξEES ( E )Ф( E ).
Спектр замедляющихся нейтронов в водородсодержащей среде без поглощения
Наиболее простая картина замедления нейтронов наблюдается в бесконечной гомогенной замедляющей среде, состоящей только из атомов водорода (ε=0, ξ=1), и в отсутствие поглощения нейтронов. В такой среде нейтрон после каждого столкновения сохраняется и с одинаковой вероятностью приобретает любую энергию меньше исходной. Хотя в процессе замедления нейтроны рассекаются по объему вещества, в случае равномерно распределенных источников по как угодно большому объему в любой единице объема число нейтронов с данной энергией будет одинаковым.
Для нахождения энергетического распределения нейтронов воспользуемся равнением баланса нейтронов в интервале энергии dE .
Число нейтронов, исчезающих из интервала dE в результате рассеяний, которые изменяют энергию нейтрона до величины, выходящей за пределы интервала, в стационарном состоянии равно числу нейтронов, которые попадают в от интервал в результате рассеяний из области энергии Е’>Е.
Так как Σа=0, то убыль нейтронов из интервала dE обусловлена только рассеянием нейтронов и равна скорости рассеяний в интервале dE — Σ S E)Ф(E)dE. Плотность потока замедляющихся нейтронов обычно относится к единичному энергетическому интервалу и является функцией энергии; [Ф(E)]=1/(см с эВ); Ф( E ) dE — плотность потока нейтронов, энергия которых лежит в интервале Е÷ E + dE .
Доля нейтронов с начальной энергией E '≤ E 0 , попадающих в результате столкновения с ядром в энергетический интервал dE , представляет собой отношение ширины этого интервала к полной ширине ступеньки замедления (1-ε)Е'. Для водорода ширина такой ступеньки равна Е' и указанная доля равна dE / E '.
Число столкновений в интервале dE ' при энергии Е' равно 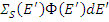 . Число нейтронов, попавших в dE из dE ', равно
. Число нейтронов, попавших в dE из dE ', равно 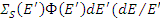 , а из всего интервала от E до E 0 равно
, а из всего интервала от E до E 0 равно 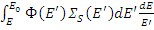 .
.
Число нейтронов, испытавших (после рождения от источника) первое рассеяние при энергии E 0 , равно S 0 . Число нейтронов, попавших в интервал dE после первого рассеяния, равно S 0 ( dE / E 0 ).
Уравнение баланса нейтронов:
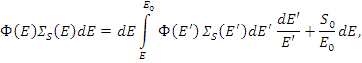
иначе
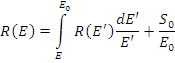
Продифференцировав уравнение по Е, получим
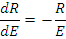
Решение уравнения есть
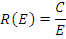
а константа С определяется подстановкой решения в интегральное уравнение при Е=Е0; C = S 0 .
Окончательное решение для среды из атомов водорода имеет вид
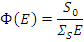
Спектр замедляющихся нейтронов в произвольной среде без поглощения
При замедлении в средах с ξ<1 при энергиях близких к E 0 , возникают особенности в распределении Ф(Е), однако при снижении Е особенности исчезают и распределение плотности потока описывается асимптотическим выражением
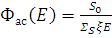 - спектр Ферми.
- спектр Ферми.
В промежуточной области 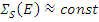 поэтому плотность потока замедляющихся нейтронов обратно пропорциональна энергии. Причина такого увеличения в том, что при замедлении уменьшается средняя потеря энергии на столкновение
поэтому плотность потока замедляющихся нейтронов обратно пропорциональна энергии. Причина такого увеличения в том, что при замедлении уменьшается средняя потеря энергии на столкновение 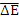 и, чтобы пройти единичный интервал энергии, требуется больше актов рассеяния.
и, чтобы пройти единичный интервал энергии, требуется больше актов рассеяния.
Плотность замедления в среде без поглощения постоянна и равна мощности источников:
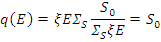
Спектр Ферми в шкале летаргии
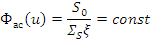
Если источник - нейтроны деления, спектр Ферми справедлив при u>5, для моноэнергетического — при любом и.
Спектр замедляющихся нейтронов в водородсодержащей среде с поглощением
Уравнение замедления при учете поглощения нейтронов усложняется. Допустим, что замедлитель - водород, а поглотителя мало:
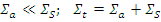
Уравнение баланса нейтронов
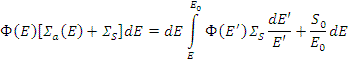
Дифференцируя данное уравнение, получим
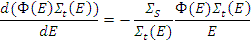
Решение этого уравнения
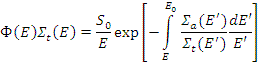
Спектр нейтронов можно записать в следующем виде:
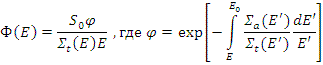
В выражении для плотности потока нейтронов появился дополнительный экспоненциальный множитель, меньший единицы. Этот же множитель появляется и в выражении для плотности замедления q ( E ), что означает, что до энергии Е доходят не все нейтроны, а только часть их, не поглотившаяся при более высоких энергиях.
Физический смысл коэффициента φ: это отношение числа нейтронов, достигших энергии Е при замедлении, к числу нейтронов, которые начали процесс замедления. Так как поглощение происходит в основном в резонансной области, то φ - вероятность избежать резонансного поглощения при замедлении нейтронов до энергии Е (произвольной энергии).
 Сечение поглощения возрастает вблизи энергии каждого резонанса, соответственно возрастает полное сечение
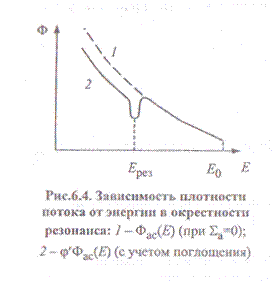
Сечение поглощения возрастает вблизи энергии каждого резонанса, соответственно возрастает полное сечение 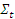 . Это обусловливает снижение плотности потока нейтронов (рис.6.4). После прохождения резонанса сечение
. Это обусловливает снижение плотности потока нейтронов (рис.6.4). После прохождения резонанса сечение 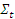 восстанавливается до
восстанавливается до 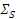 и соответственно восстанавливается плотность потока. Однако плотность потока составляет долю φ' от плотности потока без резонанса, если вероятность избежать резонансного поглощения в данном резонансе есть φ'.
и соответственно восстанавливается плотность потока. Однако плотность потока составляет долю φ' от плотности потока без резонанса, если вероятность избежать резонансного поглощения в данном резонансе есть φ'.
Выражение для плотности потока замедляющихся нейтронов при использовании летаргии
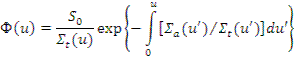
Если в среде без поглощения Ф(u)=const, то при наличии - гладкая функция, убывающая с возрастанием и.
Спектр замедляющихся нейтронов в произвольной среде с поглощением
Спектр нейтронов в такой среде записывается в виде
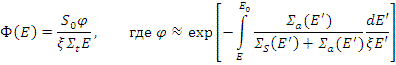
Если среда - смесь, то используется усредненная величина ξ( ξ → ξ).
Спектр нейтронов в реакторе
Замедляющиеся нейтроны распределены по энергетическому спектру, близкому к спектру Ферми. В результате замедления нейтроны становятся тепловыми. В реакторах на тепловых нейтронах плотность потока всех тепловых нейтронов и плотность потока нейтронов всех остальных энергий примерно равны. Соответственно концентрация тепловых нейтронов много больше, чем нетепловых.
Тепловые нейтроны при столкновениях с ядрами среды также теряют свою энергию либо приобретают - в зависимости от величины и направления скорости ядер-мишеней. При этом некоторая часть тепловых нейтронов будет иметь энергию, меньшую средней энергии теплового движения ядер среды, а другая часть — большую. Установление теплового равновесия между нейтронами и ядрами среды называется термализацией. Граница между областями замедления и термализации определяется, главным образом, температурой среды - при 300 К Eгр=0,2 эВ, при 1000К Егр=0,625 эВ.
Энергетическое распределение тепловых нейтронов в слабо поглощающих средах является распределением Максвелла:
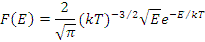
где 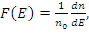 эВ-1 - доля тепловых нейтронов в единице объема в единичном энергетическом интервале, имеющих энергию Е; п0 - полное число тепловых нейтронов в единице объема; T—абсолютная температура среды;
эВ-1 - доля тепловых нейтронов в единице объема в единичном энергетическом интервале, имеющих энергию Е; п0 - полное число тепловых нейтронов в единице объема; T—абсолютная температура среды;
k=8,62 10-5 эВ/К - постоянная Больцмана.
 Данное распределение показано на рис.6.5. Средняя энергия спектра Максвелла равна (3/2) k Т, а энергия максимума распределения (наиболее вероятная энергия) — (1/2) k Т [5]. За стандартную тепловую энергию Ест принимают энергию k Т, что удобно, поскольку k Т— параметр распределения Максвелла. При
Данное распределение показано на рис.6.5. Средняя энергия спектра Максвелла равна (3/2) k Т, а энергия максимума распределения (наиболее вероятная энергия) — (1/2) k Т [5]. За стандартную тепловую энергию Ест принимают энергию k Т, что удобно, поскольку k Т— параметр распределения Максвелла. При
нормальной температуре T=TН=293 К (20° С) kT=0,025 эВ, что соответствует скорости нейтронов 2200 м/с. В таблицах сечений приводятся значения при стандартной энергии Ест при нормальной температуре.
Средняя энергия тепловых нейтронов оказывается несколько выше средней энергии теплового движения молекул среды. Это означает, что теплового равновесия нейтронов с молекулами среды не устанавливается. Причина заключается в поглощении нейтронов, а скорость поглощения выше при меньших скоростях нейтронов. Кроме того, происходит пополнение их числа со стороны более высоких энергий при замедлении. Тем не менее, распределение нейтронов близко спектру Максвелла, но соответствующему более высокой температуре, чем температура среды. Эта температура нейтронного газа ТНГ равна:
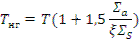
где 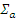 — макроскопическое сечение поглощения тепловых нейтронов при энергии k Т;
— макроскопическое сечение поглощения тепловых нейтронов при энергии k Т; 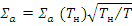 ;
; 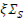 - замедляющая способность среды с энергией 1 эВ [7].
- замедляющая способность среды с энергией 1 эВ [7].
Дата: 2019-04-23, просмотров: 1067.