Рассматривается элементарная теория замедления, в которой предполагается, что во всем энергетическом интервале от 1 эВ до 10 МэВ нейтроны теряют (энергию только в результате упругого рассеяния на неподвижных и свободных ядрах. Упругое рассеяние на легких ядрах наиболее эффективно для замедления нейтронов до тепловой энергии. Неупругое рассеяние существенно лишь для замедления быстрых нейтронов, энергетические пороги исключают замедление нейтронов меньших энергий путем неупругого рассеяния.
Акт рассеяния
Для получения характеристик рассеяния рассматривается отдельный акт упругого рассеяния в системе центра инерции, в которой подавляющее число столкновений равновероятно на любой угол.
В лабораторной системе координат движение частиц рассматривается относительно границ системы, а в системе центра инерции (масс) — относительно некоторого центра, движущегося равномерно и прямолинейно относительно границ системы.
Рассмотрим акт рассеяния на неподвижном (в лабораторной системе координат) ядре (рис.6.1).
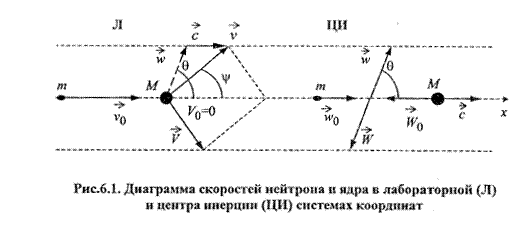
Законы сохранения количества движения и энергии справедливы для обеих систем. В лабораторной системе:
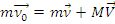 (6.1)
(6.1)
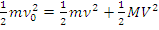 (6.2)
(6.2)
Скорость центра инерции с принимается соответствующей выражению
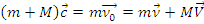
Она равна
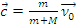 , (6.3)
, (6.3)
и ее направление (в рассматриваемом частном случае) совпадает с направлением скорости движения нейтрона до столкновения.
В системе центра инерции скорости равны:
- до столкновения
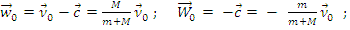 (6.4)
(6.4)
- после столкновения М
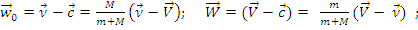 (6.5)
(6.5)
Рассчитав количества движения до и после столкновения с учетом последних четырех выражений, получим
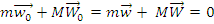 (6.6)
(6.6)
т.е. полное количество движения в системе ЦИ сохраняется и равно нулю до и после столкновения, откуда следует:
 (6.7)
(6.7)
т.е. скорости нейтрона и ядра в системе ЦИ противоположны до и после столкновения. Подставив промежуточные записи из выражений (6.4) и (6.5) в выражение закона сохранения энергии в лабораторной системе (6.2), получим
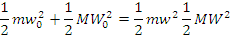
т.е. кинетическая энергия в системе центра инерции сохраняется. Подстановка соотношений (6.7) в последнее выражение дает
wo = w ; WQ = W . (6.8)
Итак, абсолютные значения скоростей нейтрона и ядра в системе ЦИ не изменяются при столкновении, изменяется лишь ориентация этих скоростей.
Теперь можно рассчитать потерю энергии нейтроном при столкновении с неподвижным ядром.
Скорость нейтрона в лабораторной системе (см. (6.5) и рис.6.1):
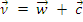 ;
; 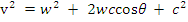 ,
,
где 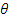 - угол рассеяния в системе центра инерции, соответствующий углу ψ в лабораторной системе;
- угол рассеяния в системе центра инерции, соответствующий углу ψ в лабораторной системе; 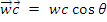 — скалярное произведение векторов). С учетом (6.3), (6.8) и (6.4) получим соответственно
— скалярное произведение векторов). С учетом (6.3), (6.8) и (6.4) получим соответственно
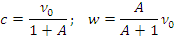
Тогда 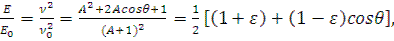
Где 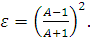
Энергия нейтрона после столкновения с ядром будет равна первоначальной (E — E 0 ) при угле рассеяния 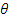 =0, минимальная энергия
=0, минимальная энергия 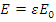 при
при 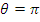 - лобовом столкновении и рассеянии в обратном направлении. При лобовом столкновении с протоном (
- лобовом столкновении и рассеянии в обратном направлении. При лобовом столкновении с протоном ( 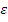 =0) Е=0, при лобовом столкновении с тяжелым ядром, характеризующимся большим значением A (
=0) Е=0, при лобовом столкновении с тяжелым ядром, характеризующимся большим значением A ( 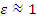 ) E ≈ E 0 , т.е. нейтрон теряет мало энергии.
) E ≈ E 0 , т.е. нейтрон теряет мало энергии.
Соотношение между углами рассеяния в системе центра инерции и лабораторной системе получаем, проецируя скорости на ось х (рис.6.1):
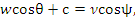
откуда
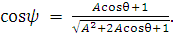 (6.9)
(6.9)
Углы рассеяния в лабораторной системе меньше, чем в системе ЦИ, но предельные значения совпадают, кроме случая А=1, когда углу θ=π соответствует о ψ=π/2 (с E=0).
Рассеяние изотропно (равновероятно на любой угол) в системе ЦИ для подавляющего числа столкновений. При этом средний косинус угла рассеяния
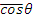 = 0, что соответствует углу рассеяния θ=π/2. Угловое распределение расcеянных нейтронов не изотропно при высоких энергиях (Е0>1 кэВ) и в области тепловых энергий (влияние химических связей). С учетом выражения (6.9) можно получить выражение для среднего косинуса угла рассеяния в лабораторной системе координат:
= 0, что соответствует углу рассеяния θ=π/2. Угловое распределение расcеянных нейтронов не изотропно при высоких энергиях (Е0>1 кэВ) и в области тепловых энергий (влияние химических связей). С учетом выражения (6.9) можно получить выражение для среднего косинуса угла рассеяния в лабораторной системе координат:
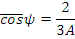
Средний косинус угла рассеяния может служить мерой асимметрии рассеяния. При большом A 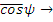
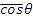 и рассеяние становится сферически симметричным в лабораторной системе координат.
и рассеяние становится сферически симметричным в лабораторной системе координат.
Наибольшая асимметрия наблюдается при А=1, т.е. при рассеянии на протонах - рассеяния в обратном направлении не может быть, всегда ψ<π/2, а
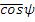 = 2/3 (ψ=48°).
= 2/3 (ψ=48°).
Закон рассеяния
При сферически симметричном рассеянии в системе ЦИ любое значение энергии после рассеяния в лабораторной системе координат оказывается равновероятным в пределах от Emax = E 0 до Еmin=εЕ0 (рис.6.2).
 Плотность вероятности энергии нейтрона после рассеяния —
Плотность вероятности энергии нейтрона после рассеяния — 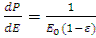
при этом 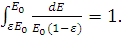
Средняя потеря энергии 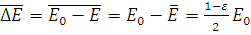
Средняя доля потерянной нейтроном энергии 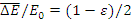 , она зависит только от массы ядра, с которым сталкивается нейтрон. При столкновении с
, она зависит только от массы ядра, с которым сталкивается нейтрон. При столкновении с
протоном 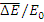 =1/2, с тяжелым ядром (А>>1) -
=1/2, с тяжелым ядром (А>>1) - 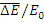 ≈2/A.
≈2/A.
Дата: 2019-04-23, просмотров: 363.