Власичев Г.Н.
В 58 Физика ядерных реакторов: учеб. пособие / Г.Н. Власичев; Нижего-род. гос. техн. ун-т им. Р.Е. Алексеева. Нижний Новгород, 2008. - 106 с. ISBN 978-5-93272-596-2
Рассмотрены физические основы теории ядерных реакторов, являющихся аппаратами для получения ядерной энергии, производства новых изотопов, а также пучков нейтронов, находящих в последние годы применение в клинической медицине. Изложены общие сведения о ядерных реакторах, взаимодействии нейтронов различных энергий с ядрами, цепной реакции деления, даны основы теории замедления и диффузии нейтронов, методики расчета коэффициента размножения нейтронов и критических размеров реактора, приведены основы кинетики.
Предназначено для студентов старших курсов специальностей 200402, 140101, 140404, обучающихся в институте ядерной энергетики и технической физики (ИЯЭиТФ), а также может быть полезно студентам специальности 140305.
Рис. 46. Табл. 16. Библиогр.: 7 назв.
УДК 621.039.5
ББК 31.46
ISBN 978-5-93272-596-2
© Нижегородский государственный
технический университет
им. Р.Е. Алексеева, 2008
© Власичев Г.Н., 2008
ОГЛАВЛЕНИЕ
| ВВЕДЕНИЕ | 5 |
| I. ОБЩИЕ СВЕДЕНИЯ О ЯДЕРНЫХ РЕАКТОРАХ | 6 |
| 1.1. Ядерный реактор как источник энергии | 6 |
| 1.2. Основные составные части реактора и их назначение | 7 |
| 1.3. Классификация реакторов по различным признакам | 7 |
| 2. ПАРАМЕТРЫ И ВИДЫ ВЗАИМОДЕЙСТВИЯ НЕЙТРОНОВ С ЯДРАМИ | 9 |
| 2.1. Понятие микроскопического сечения | 9 |
| 2.2. Понятия плотности потока нейтронов и макроскопического сечения | 10 |
| 2.3. Виды взаимодействия нейтронов с ядрами. | 11 |
| 3. ВЗАИМОДЕЙСТВИЕ НЕЙТРОНОВ РАЗЛИЧНЫХ ЭНЕРГИЙ С ЯДРАМИ | 13 |
| 3.1. Быстрые нейтроны | 13 |
| 3.2. Промежуточные (резонансные) нейтроны | 15 |
| 3.3. Медленные нейтроны | 19 |
| 3.4. Основные закономерности взаимодействия нейтронов с ядрами | 20 |
| 4. ПРОЦЕСС ДЕЛЕНИЯ И ПАРАМЕТРЫ, ЕГО ОПРЕДЕЛЯЮЩИЕ | 22 |
| 5. ЦЕПНАЯ РЕАКЦИЯ ДЕЛЕНИЯ | 27 |
| 6. ЗАМЕДЛЕНИЕ НЕЙТРОНОВ | 33 |
| 6.1. Характеристики замедления нейтронов | 33 |
| 6.2. Спектр замедляющихся нейтронов в бесконечной среде | 38 |
| 6.3. Спектр нейтронов в реакторе | 42 |
| 7. ДИФФУЗИЯ МОНОЭНЕРГЕТИЧЕСКИХ НЕЙТРОНОВ В ОДНОРОДНОЙ СРЕДЕ | 44 |
| 7.1. Характеристики диффузии нейтронов | 44 |
| 7.2. Плотность тока нейтронов, закон Фика | 45 |
| 7.3. Уравнение диффузии | 47 |
| 7.4. Альбедо | 54 |
| 8. ДИФФУЗИЯ ЗАМЕДЛЯЮЩИХСЯ НЕЙТРОНОВ | 55 |
| 9. КОЭФФИЦИЕНТ РАЗМНОЖЕНИЯ НЕЙТРОНОВ В БЕСКОНЕЧНОЙ СРЕДЕ | 61 |
| 9.1. Число нейтронов на акт поглощения | 61 |
| 9.2. Коэффициент размножения на быстрых нейтронах | 62 |
| 9.3. Вероятность избежать резонансного захвата | 62 |
| 9.4. Коэффициент использования тепловых нейтронов | 67 |
| 9.5. Усреднение сечений в области тепловых нейтронов | 69 |
| 9.6. Оптимальные параметры размножающих сред | 69 |
| 9.7. Длина диффузии и возраст нейтронов в размножающей среде | 70 |
| 10. КРИТИЧЕСКИЕ РАЗМЕРЫ ГОМОГЕННОГО РЕАКТОРА БЕЗ ОТРАЖАТЕЛЯ | 72 |
| 11. КРИТИЧЕСКИЕ РАЗМЕРЫ ГОМОГЕННОГО РЕАКТОРА С ОТРАЖАТЕЛЕМ | 81 |
| 12. НЕСТАЦИОНАРНЫЙ РЕЖИМ РЕАКТОРА БЕЗ ОТРАЖАТЕЛЯ | 85 |
| 12.1. Нестационарное уравнение диффузии | 85 |
| 12.2. Период реактора | 88 |
| 12.3. Учет запаздывающих нейтронов | 89 |
| 12.4. Кинетика реактора с учетом запаздывающих нейтронов | 90 |
| 12.5. Решение уравнений кинетики с учетом шести групп запаздывающих нейтронов | 93 |
| 12.6. Зависимость установившегося периода реактора от величины скачка реактивности | 95 |
| 12.7. Решение уравнений кинетики с учетом одной группы запаздывающих нейтронов | 97 |
| 12.8. Кинетика реактора при отрицательном скачке реактивности | 103 |
| СПИСОК ЛИТЕРАТУРЫ | 105 |
ВВЕДЕНИЕ
Ядерные реакторы в настоящее время применяются преимущественно для получения ядерной энергии - выработки электроэнергии, энергообеспечения и движения военных кораблей и гражданских судов. Перспективно получение тепловой энергии для коммунального хозяйства, использование высокотемпературного тепла для получения водорода, а также в металлургических процессах и других производствах. Ядерные реакторы находят применение в производстве делящихся материалов и радиоактивных изотопов для нужд обороны, промышленности, науки, медицины и других отраслей. Студенты, обучающиеся в институте ядерной энергетики и технической физики, должны иметь представление об устройстве ядерного реактора и об основных физических процессах, происходящих в реакторе.
На достижениях ядерной энергетики базируется медицинская радиология - молодая наукоемкая дисциплина, без которой сегодня не может обойтись ни один раздел клинической медицины. Существуют методики лучевой терапии с использованием протонов, нейтронов, электронов, фотонов, испускаемых радиоизотопами, получаемыми на ускорителях, а также в ядерных реакторах. В лучевой терапии нуждаются многие больные с опухолями. Выделим некоторые из лечебных технологий, в основу которых положены последние достижения в атомной энергетике: новый высокоэффективный метод сочетанной гамма-нейтронной терапии с использованием быстрых реакторных нейтронов на базе ( г. Обнинск); разрабатываемый медицинский блок на реакторе ВВРц НИВХИ им. Карпова ( г. Обнинск) для нейтронной и нейтрон-захватной терапии[1].
Учебное пособие посвящено физическим основам теории ядерных реакторов. Изложены общие сведения о ядерных реакторах, взаимодействии нейтронов различных энергий с ядрами, цепной реакции деления, даны основы теории замедления и диффузии нейтронов, методики расчета коэффициента размножения нейтронов и критических размеров реактора, приведены основы кинетики.
Рис. 1.1. Зависимость средней энергии связи,
С ЯДРАМИ
Процесс образования новых ядер или частиц при столкновениях частиц и ядер называется ядерной реакцией. Если при столкновениях сохраняются исходное ядро и частица, и не образуются новые, то процесс называется рассеянием.
Ядерные концентрации
Макроскопическое сечение взаимодействия нейтронов с ядрами типа k- Σk=Nkσk, где Nk — концентрация ядер типа k . В среде, состоящей из ядер одного
типа - N = 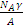 , Где NA =6,023 10 1/моль-число Авогадро; γ -плотность;
, Где NA =6,023 10 1/моль-число Авогадро; γ -плотность;
[γ]=г/см ; А — атомная масса; [А]- г/молъ. В химических соединениях -
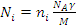 , где М — молекулярная масса; ni —число атомов i-го элемента в молекуле. В смеси материалов
, где М — молекулярная масса; ni —число атомов i-го элемента в молекуле. В смеси материалов 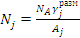 , где
, где 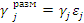 - размазанная плотность; εj- объемная доля j-го материала. Обобщенная формула -
- размазанная плотность; εj- объемная доля j-го материала. Обобщенная формула - 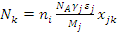 , где xjk - обогащение i-го химического элемента по изотопу k .
, где xjk - обогащение i-го химического элемента по изотопу k .
С ЯДРАМИ
Для каждого нуклида зависимости сечений от энергии представляют собой сложные кривые, имеющие различные формы в отдельных энергетических интервалах.
Выделяются три интервала (области) энергий нейтронов: быстрые (Е>1МэВ), промежуточные (резонансные) (1 эВ<E<1 МэВ), медленные (E<1эВ). Быстрые нейтроны могут вызвать деление U238. В область быстрых нейтронов часто включается область, примыкающая к резонансам для тяжелых ядер с Е>1 кэВ [7]. Среди медленных нейтронов выделяют тепловые нейтроны с Е<0,2 эВ, которые находятся в равновесии с окружающей средой. Граница пропускания нейтронов кадмием (равна 0,625 эВ) тоже часто используется в качестве границы области тепловых нейтронов [7].
Выделяются три типа ядер, различающихся атомным весом: легкие (А<10), средние (10<A<200), тяжелые (A>200).
Быстрые нейтроны
В области энергий быстрых нейтронов имеют место все виды взаимодействия.
Полное сечение σt при больших энергиях нейтронов имеет плавный характер и медленно уменьшается с ростом энергии, оно увеличивается с ростом массового числа А. Числовое значение его можно приближенно оценить по формуле 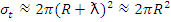 . Последнее справедливо при очень высоких Е для достаточно тяжелых ядер. Полное сечение состоит практически из двух (приблизительно равных): сечения потенциального рассеяния σр и сечения образования составного ядра σcomp , т.е. σp ≈ σcomp ≈π(R+ ƛ)2 . В области энергий быстрых нейтронов для большинства ядер эти значения равны нескольким барнам.
. Последнее справедливо при очень высоких Е для достаточно тяжелых ядер. Полное сечение состоит практически из двух (приблизительно равных): сечения потенциального рассеяния σр и сечения образования составного ядра σcomp , т.е. σp ≈ σcomp ≈π(R+ ƛ)2 . В области энергий быстрых нейтронов для большинства ядер эти значения равны нескольким барнам.
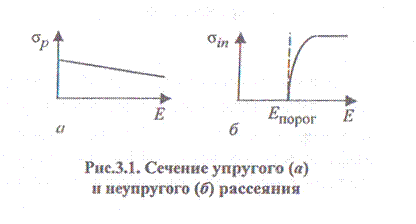 Для быстрых нейтронов сечение упругого рассеяния равно приблизительно сечению потенциального рассеяния, поскольку вероятность резонансного рассеяния мала. Но это не относится к легким ядрам. Сечение потенциального рассеяния уменьшается с увеличением энергии быстрых нейтронов (рис.3.1). Сечение образования составного ядра для неделящихся ядep в большей части области энергий быстрых нейтронов практически равно сечению неупругого рассеяния, для делящихся ядер - сечению неупругого рассеяния плюс сечению деления.
Для быстрых нейтронов сечение упругого рассеяния равно приблизительно сечению потенциального рассеяния, поскольку вероятность резонансного рассеяния мала. Но это не относится к легким ядрам. Сечение потенциального рассеяния уменьшается с увеличением энергии быстрых нейтронов (рис.3.1). Сечение образования составного ядра для неделящихся ядep в большей части области энергий быстрых нейтронов практически равно сечению неупругого рассеяния, для делящихся ядер - сечению неупругого рассеяния плюс сечению деления.
 Неупругое рассеяние возможно, если налетающий нейтрон имеет энергию, достаточную для того, чтобы ядро после рассеяния осталось, по крайней мере, в первом возбужденном состоянии, т.е. энергия нейтрона должна превышать порог. Пороговая энергия с увеличением А уменьшается в среднем примерно от 1 МэВ до 100 кэВ (табл.3.1). Для делящихся изотопов энергия первого возбужденного состояния на несколько кэВ выше энергии основного состояния. Сечение неупругого рассеяния с ростом А растет.
Неупругое рассеяние возможно, если налетающий нейтрон имеет энергию, достаточную для того, чтобы ядро после рассеяния осталось, по крайней мере, в первом возбужденном состоянии, т.е. энергия нейтрона должна превышать порог. Пороговая энергия с увеличением А уменьшается в среднем примерно от 1 МэВ до 100 кэВ (табл.3.1). Для делящихся изотопов энергия первого возбужденного состояния на несколько кэВ выше энергии основного состояния. Сечение неупругого рассеяния с ростом А растет.
Сечение поглощения для неделящихся ядер — сечение радиационного захвата, т.е. σа=σγ, для тяжелых делящихся ядер σа=σγ +σf ≈σf.
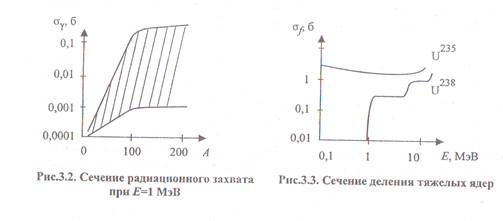 Сечение радиационного захвата в области энергий быстрых нейтронов изменяется по закону σγ ≈const/E. С ростом массового числа А (рис.3.2) сечение радиационного захвата при данной энергии растет, причем в области малых и средних А рост сечения довольно резкий, затем рост уменьшается и в области больших А - слабый. Для тяжелых ядер сечение σγ практически постоянно и равно приблизительно 0,1 б. Наименьшие значения σγ имеют четно-четные (особенно магические) ядра. Такие вещества лучше всего использовать в качестве материалов замедлителя и теплоносителя. Вещества с нечетным числом протонов и/или нейтронов лучше всего использовать в качестве материала защиты.
Сечение радиационного захвата в области энергий быстрых нейтронов изменяется по закону σγ ≈const/E. С ростом массового числа А (рис.3.2) сечение радиационного захвата при данной энергии растет, причем в области малых и средних А рост сечения довольно резкий, затем рост уменьшается и в области больших А - слабый. Для тяжелых ядер сечение σγ практически постоянно и равно приблизительно 0,1 б. Наименьшие значения σγ имеют четно-четные (особенно магические) ядра. Такие вещества лучше всего использовать в качестве материалов замедлителя и теплоносителя. Вещества с нечетным числом протонов и/или нейтронов лучше всего использовать в качестве материала защиты.
Сечение деления (σf) не равно нулю только для ядер с А>230. Сечения деления четно-четных ядер имеют пороговый характер (рис.3.3). Пороговое значение энергии для U238 - ~ 1МэВ. Сечения четно-четных ядер с ростом энергии
сверх пороговых значений быстро увеличиваются, достигая примерно постоянных значений, меньших соответствующих сечений для четно-нечетных ядер.
 3.2. Промежуточные (резонансные) нейтроны
3.2. Промежуточные (резонансные) нейтроны
Полное сечение взаимодействий в этой области можно разделить на две части: с образованием и без образования составного ядра.
Ядро - система связанных (не свободных) нуклонов, следовательно, оно обладает дискретным спектром энергии. В обычных условиях оно находится в наиболее низком энергетическом состоянии, которое называют основным. Состояния с большей энергией называются возбужденными. Зависимость плотности вероятности пребывания ядра в каком-либо энергетическом состоянии от энергии имеет резонансный характер. Вероятность того, что энергия ядра заключается в некотором интервале вблизи уровня одного из возбужденных состояний, значительно выше того, что она находится в промежутках между уровнями.
При захвате ядром нейтрона ему передается энергия, равная сумме кинетической энергии нейтрона и энергии связи нейтрона. При этом ядро переводится в возбужденное состояние. Если величина переданной ему энергии не совпадает с энергией возбуждения одного из энергетических состояний ядра, то вероятность образования составного ядра мала.
Во всех возбужденных состояниях ядро может находиться лишь конечное время до тех пор, пока возбуждение не будет снято тем или иным путем. Время жизни составного ядра (и относительно его распада и относительно испускания γ-кванта) значительно превосходит время пролета нейтроном области ядра R / v , де R - радиус ядра; ν - скорость нейтрона. Между энергией возбужденного состояния и его временем жизни имеет место соотношение неопределенностей Гейзенберга ∆ E ∆ t =ħ, где ∆Е - ширина уровня энергии (ее можно измерить).
Таким образом, каждый уровень имеет вполне определенную ширину. За ширину уровня Г принимают ширину резонанса на половине его высоты. Тогда время жизни данного состояния определяется выражением τ=ħ /Г. Так как величина, обратная времени жизни, есть вероятность распада в единицу времени, то Г определяет также вероятность распада ядра. Поскольку такой распад в общем случае происходит различными способами, то введено понятие парциальной ширины уровня Гi, которая характеризует вероятность распада ядра по i-му каналу.
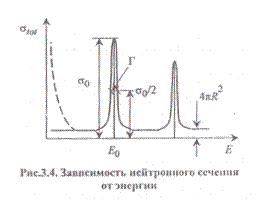 При взаимодействии промежуточных нейтронов с тяжелыми ядрами составные ядра возбуждаются до состояний, для которых ширина уровней меньше расстояний между уровнями энергии.
При взаимодействии промежуточных нейтронов с тяжелыми ядрами составные ядра возбуждаются до состояний, для которых ширина уровней меньше расстояний между уровнями энергии.
В этом случае резко проявляется роль отдельных уровней состояний ядра, т.е. зависимости сечений образования и распада составного ядра от энергии нейтрона имеют резонансный характер (рис.3.4).
В области энергий промежуточных нейтронов с заметной вероятностью происходят упругое рассеяние (потенциальное и резонансное), радиационный захват и деление ядер. Деление возможно лишь для самых тяжелых ядер с нечетным числом нейтронов – U233, U235 , Pu239 . Полное сечение: σt≈σγ +σf +σel , где σel = σp +σr .
Сечение образования составного ядра вблизи одиночного изолированного уровня (формула Брейта - Вигнера):
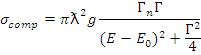
а сечения различных i -x процессов, идущих через стадию составного ядра.
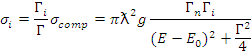
где 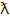 - длина волны нейтрона;
- длина волны нейтрона; 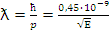 , см; [Е]—эВ; g - статистический весовой множитель;
, см; [Е]—эВ; g - статистический весовой множитель; 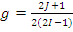 ; I - спин ядра-мишени; J — спин составного ядра; Е0 - резонансная энергия; i - индекс процесса (парциальной ширины), который может принимать следующие значения: r — резонансное рассеяние (n - нейтронная ширина); γ - радиационный захват (радиационная ширина); /-деление (ширина деления); Г=Гn+Гγ+Гf — полная ширина уровня; Гn, Гγ, Гf — парциальные ширины.
; I - спин ядра-мишени; J — спин составного ядра; Е0 - резонансная энергия; i - индекс процесса (парциальной ширины), который может принимать следующие значения: r — резонансное рассеяние (n - нейтронная ширина); γ - радиационный захват (радиационная ширина); /-деление (ширина деления); Г=Гn+Гγ+Гf — полная ширина уровня; Гn, Гγ, Гf — парциальные ширины.
При энергии нейтронов, равной E 0 , сечение имеет максимальное значение
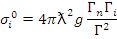
Сечение радиационного захвата
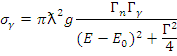
Зная параметры резонансов ( 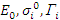 ), можно воспроизвести, пользуясь формулой Брейта — Вигнера, зависимости сечений различных процессов от энергии нейтронов и массовых чисел ядер в области энергий, где резонансы хорошо разделены.
), можно воспроизвести, пользуясь формулой Брейта — Вигнера, зависимости сечений различных процессов от энергии нейтронов и массовых чисел ядер в области энергий, где резонансы хорошо разделены.
Для тяжелых ядер первые резонансы (резонансы с меньшей энергией) – в основном резонансы радиационного захвата; при энергии 102-103 эВ - 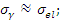 при больших энергиях происходит преимущественно резонансное рассеяние (пороги неупругого рассеяния значительно выше). Для легких ядер сечение резонансного рассеяния много больше сечения радиационного захвата при любой энергии.
при больших энергиях происходит преимущественно резонансное рассеяние (пороги неупругого рассеяния значительно выше). Для легких ядер сечение резонансного рассеяния много больше сечения радиационного захвата при любой энергии.
Расположение резонансов сильно зависит от массового числа. Чем тяжелее ядро, тем ниже резонанс и тем он мощнее. Резонансы делящихся ядер расположены при 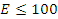 эВ, резонансы средних ядер - в интервале от 1 до 100 кэВ, ре-иансы легких ядер - в области
эВ, резонансы средних ядер - в интервале от 1 до 100 кэВ, ре-иансы легких ядер - в области 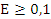 МэВ.
МэВ.
С увеличением энергии среднее расстояние между резонансами уменьшается. Резонансная область разделяется на две: разрешенных резонансов и неразрешенных резонансов. В области неразрешенных (перекрывающихся) резонансов ширины энергетических уровней составных ядер велики по сравнению с расстояниями между уровнями.
 Сечения при энергии резонансов в среднем увеличиваются с уменьшением энергии. Для тяжелых ядер эти сечения могут достигать больших значений в области первых резонансов (
Сечения при энергии резонансов в среднем увеличиваются с уменьшением энергии. Для тяжелых ядер эти сечения могут достигать больших значений в области первых резонансов ( 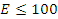 эВ). К ним относятся изотопы урана (U238) и плутония, продукты деления. Особенно велики значения σγ для резонансов некоторых продуктов деления, например, для Хе135 -σγ ≈3,3 106 б при Е0=0,08 эВ. Сечения σγ при резонансных энергиях для тяжелых и средних ядер в области первых резонансов часто значительно превышают сечения в интервале энергий новых нейтронов. Сечения, усредненные по области резонансов, также значительно превышают сечения до резонансов. Однако интервалы энергии с большими значениями сечений занимают лишь малую часть всей области резонансов. Поэтому нейтроны, уменьшающие свою энергию при потенциальном рассеянии относительно большими порциями, с большой вероятностью минуют такие интервалы. Поэтому доля поглощений в резонансной области мала для всех ядер, кроме самых тяжелых.
эВ). К ним относятся изотопы урана (U238) и плутония, продукты деления. Особенно велики значения σγ для резонансов некоторых продуктов деления, например, для Хе135 -σγ ≈3,3 106 б при Е0=0,08 эВ. Сечения σγ при резонансных энергиях для тяжелых и средних ядер в области первых резонансов часто значительно превышают сечения в интервале энергий новых нейтронов. Сечения, усредненные по области резонансов, также значительно превышают сечения до резонансов. Однако интервалы энергии с большими значениями сечений занимают лишь малую часть всей области резонансов. Поэтому нейтроны, уменьшающие свою энергию при потенциальном рассеянии относительно большими порциями, с большой вероятностью минуют такие интервалы. Поэтому доля поглощений в резонансной области мала для всех ядер, кроме самых тяжелых.
В ядерном реакторе наибольший вклад в радиационный захват резонансных нейтронов вносит и U238. У U238 в области, близкой к тепловой, сильные захватные резонансы. Резонансы тяжелых ядер характеризуются как узкие
( 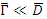 (табл.3.3) [3], где
(табл.3.3) [3], где 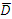 — среднее расстояние между уровнями) и поглотительные (
— среднее расстояние между уровнями) и поглотительные ( 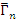 пренебрежимо мала). В табл.3.3:
пренебрежимо мала). В табл.3.3: 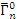 —средняя приведенная ширина;
—средняя приведенная ширина;
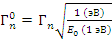
Эффект Доплера
В физике эффект Доплера — изменение частоты при движении источника звука по отношению к детектору.
Ядра среды, с которыми нейтроны испытывают соударения, имеют конечные массы и участвуют в тепловом движении. При этом скорость нейтрона в системе центра инерции (Е) не совпадает со скоростью в лабораторной системе координат (E'):
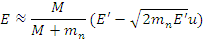
где и - проекция скорости теплового движения ядра (атома) на направление движения нейтрона.
Из формулы видно, что при одной и той же Е' величина Е может быть как больше Е' (нейтрон движется навстречу ядру), так и меньше Е' (движение в одну сторону). Это означает, что нейтрон с заданной энергией Е' будет взаимодействовать с ядрами с различными вероятностями, зависящими от скоростей ядер. Так, если Е' = E 0 (E 0-энергия резонанса), то лишь часть нейтронов будет взаимодействовать с максимальным сечением σ0 . Для остальных нейтронов будет σ<σ0 , и отличие увеличивается с ростом и ядра. Если Е' незначительно отличается от E 0 , то среди взаимодействий найдутся и такие, которые идут с сечением, большим сечения, соответствующего Е'.
Таким образом, влияние теплового движения ядер сводится к уменьшению высоты и увеличению ширины резонанса (рис.3.5) — эффект Доплера.
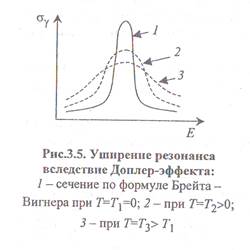 Чем меньше энергия резонанса E 0 и выше температура среды, тем сильнее проявляется Доплер-эффект.
Чем меньше энергия резонанса E 0 и выше температура среды, тем сильнее проявляется Доплер-эффект.
Практическое значение имеет влияние Доплер-эффекта на зависимость сечения радиационного захвата (и поглощения для делящихся ядер) от энергии.
Усредненное значение 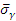 представляется в виде
представляется в виде 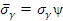 , где
, где 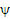 - протабулированная поправочная функция, зависящая, в частности, от доплеровской ширины резонанса -
- протабулированная поправочная функция, зависящая, в частности, от доплеровской ширины резонанса - 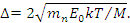
При большой температуре Т величина 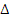 может быть больше естественной ширины Резoнанса Г, то есть действительная ширина резонанса Г+
может быть больше естественной ширины Резoнанса Г, то есть действительная ширина резонанса Г+ 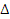 может значительно превышать Г.
может значительно превышать Г.
Медленные нейтроны
Медленные нейтроны - это нейтроны с Е<1 эВ.
Наиболее важное значение имеют нейтроны, у которых энергия близка к энергии ядер среды. Это узкая область тепловых нейтронов с Е<0,1 эВ. Она определяет физику ядерных реакторов на тепловых нейтронах.
Сечение рассеяния в области тепловых нейтронов σS = const, т.е. вдали от резонанса сечение резонансного рассеяния не зависит от энергии нейтрона, основной вклад вносит сечение потенциального рассеяния.
Сечение упругого рассеяния (практически потенциальное рассеяние) для большинства элементов - 3 σ< σS <10 б, около десяти элементов имеют σS <3 б (например, Аl27 —1,4 б), около двадцати - σS >10 б (например, Н1 — 38 б, Ni -5,6, Fe -11 б)[3].
Распад составного ядра при взаимодействии тепловых нейтронов с ядрами возможен лишь путем испускания γ-квантов. Исключение составляют деление тяжелых ядер с нечетным числом нейтронов и некоторые реакции с образованием заряженных частиц, которые имеют большие сечения, например, у В10.
Сечения взаимодействий с образованием составного ядра в области тепловой энергии можно оценить с помощью формулы Брейта - Вигнера, из которой при 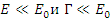 следует
следует
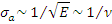
Данное соотношение справедливо и в случае неприменимости формулы Брейта — Вигнера.
Физический смысл закона 1/ν — вероятность захвата нейтрона ядром пропорциональна времени пролета нейтроном области ядра.
Закон 1/ν нарушается для элементов, имеющих резонансы вблизи или в самой тепловой области. Отклонение учитывается введением специального множителя.
Сечение поглощения (радиационного захвата) сильно изменяется в зависимости от массового числа ядер. Для большинства очень легких элементов σа мало (меньше 1 б) [3]. Например, у дейтерия σа<10-3 б. Имеются исключения у 5В σa=757,7 б. С ростом массового числа А значения σа в среднем увеличивается. Для ядер с А>50 - σа >1 б. Особенно велики σа для ядер с А>100, около десяти элементов имеют σа >1000 б. Самый большой поглотитель — ксенон 54Xe135 (осколок деления, отравитель реактора) - σа =2,7 106 б, другие поглотители: кадмий 48Cd113 - σа =20 103 б, гафний 72Hf174 - σа =1500 б.
Сечение σγ сильно зависит от четности числа протонов и нейтронов. Для
четно-четных ядер значения σγ обычно меньше. Особо малы σγ для ядер с магическим числом нейтронов или протонов, например, для Zr90 — σа =0,l б.
 Материалы наиболее благоприятные для теплоносителя, замедлителя, конструкционных материалов - элементы, у которых аномально низкие сечения поглощения. В табл.3.4 приведены сечения поглощения элементов, входящих в состав указанных материалов, при стандартной энергии при нормальной температуре [3].
Материалы наиболее благоприятные для теплоносителя, замедлителя, конструкционных материалов - элементы, у которых аномально низкие сечения поглощения. В табл.3.4 приведены сечения поглощения элементов, входящих в состав указанных материалов, при стандартной энергии при нормальной температуре [3].
 В табл.3.5 приведены значения сечения изотопов урана при стандартной энергии при нормальной температуре для изотопов урана, используемого в качестве ядерного горючего в ядерных реакторах [3].
В табл.3.5 приведены значения сечения изотопов урана при стандартной энергии при нормальной температуре для изотопов урана, используемого в качестве ядерного горючего в ядерных реакторах [3].
Полное сечение σt для тепловых нейтронов представляет собой сумму сечения рассеяния σS и сечения радиационного захвата σγ (для делящихся ядер - сечения поглощения σа) и в большинстве случаев изменяется по закону 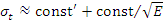 . Эта зависимость нарушается для ядер с резонансами при малых энергиях, а также из-за влияния кристаллической структуры, химических связей и теплового движения атомов.
. Эта зависимость нарушается для ядер с резонансами при малых энергиях, а также из-за влияния кристаллической структуры, химических связей и теплового движения атомов.
ЦЕПНАЯ РЕАКЦИЯ ДЕЛЕНИЯ
Цепная реакция деления — последовательность реакций деления, в которых выделяются свободные нейтроны, необходимые для деления новых ядер. - В системе, состоящей из достаточного количества ядерного горючего, возникает самоподдерживающаяся цепная реакция деления. Деление тяжелого ядра возбуждается одним нейтроном, а в результате деления появляется более одного нейтрона - необходимое условие осуществимости самоподдерживающейся цепной реакции деления. Управляемая цепная реакция деления осуществляется в активной зоне ядерного реактора.
Область состояний системы с самоподдерживающейся цепной реакцией деления отделена от области, где она невозможна, критическим состоянием. В критическом состоянии число нейтронов не меняется во времени. Достижение критического состояния определяется рядом факторов.
Размножение нейтронов можно представить как смену поколений. Каждый нейтрон, участвующий в цепном процессе, проходит цикл обращения: рождается в реакции деления, некоторое время существует в свободном состоянии, затем либо теряется, либо порождает новый акт деления и дает нейтроны следующего поколения. Поколения нейтронов при непрерывном их обращении разделены средним временем нейтронного цикла - l. Время жизни мгновенных нейтронов l в реакторах различного типа различается на пять порядков: в тяжеловодных –l ~10-2 с, в легководных- l ~ 10-4 с, в БН- l ~10-7 с. Различие вызвано разными средними временами миграции нейтронов в среде от рождения до захвата с делением.
Важнейшей характеристикой цепной реакции деления служит коэффициент размножения нейтронов: К∞ - в бесконечной однородной среде; Кэф — в ЯР, имеющем конечные размеры и поэтому утечку нейтронов за его пределы. Критическое состояние характеризуется условием Кэф =1.
Коэффициентом размножения нейтронов называется отношение числа нейтронов данного поколения к их числу в предшествующем поколении во всем объеме размножающей нейтроны среды:
Кэф = Nn/Nn -1
Где п — номер цикла; N — число нейтронов.
Изменение числа нейтронов в некритическом реакторе определяется отличием коэффициента Кэф от единицы и временем нейтронного цикла l. Если в некоторый момент времени в реакторе имеется N нейтронов, то по определению коэффициента размножения их число по прошествии одного цикла обращения станет равным Кэф N , а приращение числа нейтронов за время цикла составит Кэф N — N =(Кэф-1) N . Следовательно, изменение числа нейтронов в единицу времени
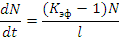
Решение этого уравнения дает зависимость числа нейтронов от времени
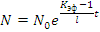
где N 0 — число нейтронов в момент t=0.
Такая же зависимость и для плотности нейтронов:
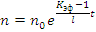
В соответствии с данной зависимостью изменяется плотность энерговыделения в системе или мощность реактора.
Управление цепной реакцией деления в реакторе осуществляется изменением величины Кэф за счет перемещения стержней с сильно поглощающим нейтроны материалом. Если Кэф =1, то плотность нейтронов и соответственно мощность реактора не меняются. Если Кэф >1, то реактор экспоненциально набирает мощность. Для вывода реактора на некоторый уровень мощности с уровня нулевой или меньшей мощности вводится на некоторое время небольшая надкритичность, после достижения необходимого уровня реактор возвращают в критическое состояние (рис.5.1). Для остановки реактор вводится в подкритическое состояние с Кэф < 1.
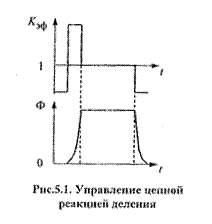 В приведенной зависимости не учитываются запаздывающие нейтроны, но если Кэф -1 больше доли запаздывающих нейтронов β, то развитие цепной реакции во времени происходит практически в соответствии с этой зависимостью. При Кэф =1,01 число нейтронов в легководном реакторе с l~10-3 с возрастает каждую секунду в ехр(0,01 1/0,001)=ехр(10)≈20000 раз. В управляемой установке такое значение Кэф недопустимо.
В приведенной зависимости не учитываются запаздывающие нейтроны, но если Кэф -1 больше доли запаздывающих нейтронов β, то развитие цепной реакции во времени происходит практически в соответствии с этой зависимостью. При Кэф =1,01 число нейтронов в легководном реакторе с l~10-3 с возрастает каждую секунду в ехр(0,01 1/0,001)=ехр(10)≈20000 раз. В управляемой установке такое значение Кэф недопустимо.
Коэффициент размножения нейтронов можно определить так же, как отношение скоростей генерации и потерь нейтронов:
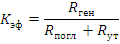
где Rген - число генерируемых нейтронов в единицу времени; Rпогл - число поглощаемых нейтронов в единицу времени; 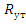 - число утекающих нейтронов в единицу времени. Скорости Rген и Rпогл - интегральные по энергии нейтронов и объему реактора,
- число утекающих нейтронов в единицу времени. Скорости Rген и Rпогл - интегральные по энергии нейтронов и объему реактора, 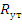 - интегральная по энергии нейтронов и поверхности реактора.
- интегральная по энергии нейтронов и поверхности реактора.
Можно представить Кэф в виде двух сомножителей:
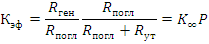
где К∞ — коэффициент размножения нейтронов в бесконечной среде; Р - вероятность избежать утечки из конечного объема.
Коэффициент К∞ определяет принципиальную способность среды размножать нейтроны. Если К∞>1, то всегда существует объем конечных размеров, в котором может быть достигнуто условие Кэф =1.
Вероятность Р зависит от размеров и формы активной зоны и может быть как угодно мала при уменьшении размеров активной зоны. Соотношение между поглощением и утечкой пропорционально 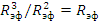 (Rэф - эффективный линейный размер), снижается при уменьшении объема тела и стремится к нулю при
(Rэф - эффективный линейный размер), снижается при уменьшении объема тела и стремится к нулю при 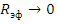 - соответственно
- соответственно 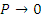 .
.
Значит, в случае К∞>1условие Кэф =1 всегда может быть выполнено.
Геометрические размеры активной зоны, которым соответствует Кэф =1, называются критическими размерами. Соответствующий объем активной зоны называется критическим объемом, а масса делящегося материала в критическом объеме - критической массой.
В заданном объеме с известным Р критическое состояние может быть достигнуто также подбором состава среды с необходимым К∞. Относительная концентрация делящегося материала в активной зоне, при которой Кэф =1, называется критической концентрацией.
Количественные оценки осуществимости самоподдерживающейся цепной
реакции деления
Для оценки возможности создания системы с Кэф >1 рассчитаем приблизительные значения К∞ в некоторых средах разного состава:
1. U238 (делящийся только быстрыми нейтронами).
В чистом виде U238 не может быть использован в качестве ядерного топлива. Для доказательства оценим значение К∞ для среды из U238 . Неупругое рассеяние снижает энергию нейтрона, как правило, до значений, меньших пороговой энергии деления U238 , т.е. неупругое рассеяние на U238 , как и радиационный захват, выводит нейтрон из цикла. Тогда
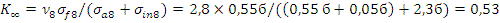
Причем полученное значение К∞ , завышено, так как часть нейтронов деления имеет энергии ниже пороговой, а другая часть обладает сечениями σf <0,55 б.
2. U235.
Чистый U235 позволяет создать критическую систему без особых проблем, когда он занимает минимальный объем:
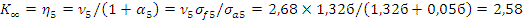
Если пренебречь замедлением нейтронов при неупругом рассеянии, можно считать, что нейтроны вызывают деление, имея Е=2 МэВ. Теперь неупругое рассеяние не исключает возможности деления ядра рассеянным нейтроном, а только переводит его в область меньших энергий, где η ненамного отличается от η при Е=2 МэВ.
Большое значение К∞ приводит к относительно малой критической массе. Критические массы шаровых тел из делящихся материалов и соответствующие размеры критических шаров:
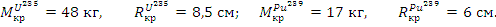
3. Смесь U235 и U238 (металлический уран) - упрощенный вариант реактора на быстрых нейтронах.
В такой среде К∞≥1 можно получить при обогащении ( N 5 / NU ) не менее 5%. Это объясняется тем, что нейтроны в металлическом уране с очень большой вероятностью испытывают неупругое рассеяние с заметным уменьшением энергии. Но при снижении энергии σγ как у U235, так и у U238 увеличивается гораздо быстрее, чем σf у U235. Это приводит к возрастанию доли радиационного захвата относительно деления — а, и при малом обогащении решающую роль играет радиационный захват U238 . Минимальное обогащение для реальных реакторов на быстрых нейтронах достигает примерно 20%.
Самоподдерживающаяся цепная реакция может быть получена в смесях природного или слабообогащенного урана с веществами-замедлителями нейтронов. При достаточных количестве и качестве замедлителя большая часть делений будет осуществляться тепловыми нейтронами. Если при высоких энергиях нейтронов сечения поглощения U235 и U238 различаются в несколько раз, то при тепловой энергии это различие достигает 250. В этом случае даже при такой малой концентрации, как в природном уране U235 поглощает нейтроны с большей вероятностью, чем U238 . Благодаря этому, число нейтронов деления, образующихся при поглощении одного теплового нейтрона ураном, - η незначительно отличается от η5 уже при относительно малых обогащениях (табл.5.1). Но величина коэффициента размножения нейтронов К∞ будет меньше η из-за поглощения нейтронов ядрами замедлителя и в U238 при замедлении.
 Таким образом, в реакторах с достаточно большим количеством замедлителя можно применять в качестве топлива уран с малым обогащением. Обогащение определяется в первую очередь видом замедлителя. При использовании в качестве замедлителя тяжелой воды, графита, бериллия критическое состояние может быть достигнуто в реакторах с топливом из природного урана.
Таким образом, в реакторах с достаточно большим количеством замедлителя можно применять в качестве топлива уран с малым обогащением. Обогащение определяется в первую очередь видом замедлителя. При использовании в качестве замедлителя тяжелой воды, графита, бериллия критическое состояние может быть достигнуто в реакторах с топливом из природного урана.
Цикл размножения нейтронов в реакторах на тепловых нейтронах
Рассмотрим один цикл размножения нейтронов в смеси топлива с достаточно большим количеством замедлителя, в которой большая часть делений осуществляется тепловыми нейтронами, в виде цепочки, изображенной на схеме рис.5.2.
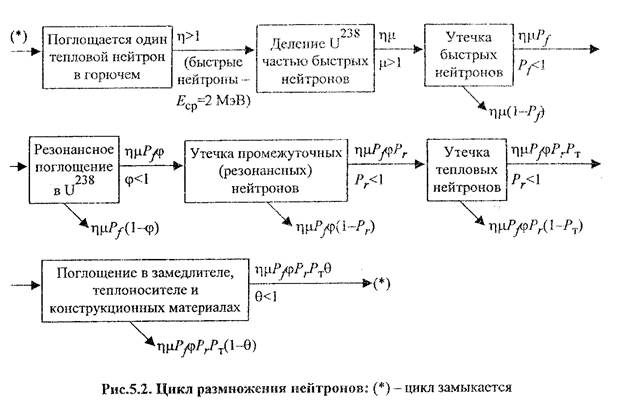
По завершении нейтронного цикла N нейтронов предыдущего поколения превращается в
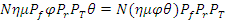
нейтронов следующего поколения.
По определению коэффициента размножения нейтронов
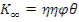 - формула четырех сомножителей,
- формула четырех сомножителей,
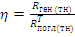 - число нейтронов, генерируемых при одном поглощении теплового нейтрона в топливе;
- число нейтронов, генерируемых при одном поглощении теплового нейтрона в топливе;
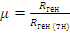 - коэффициент размножения на быстрых нейтронах;
- коэффициент размножения на быстрых нейтронах;
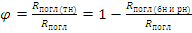 - вероятность избежать резонансного захвата (обычно в U238) или доля нейтронов, не поглотившихся при замедлении;
- вероятность избежать резонансного захвата (обычно в U238) или доля нейтронов, не поглотившихся при замедлении;
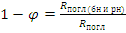 - вероятность резонансного захвата;
- вероятность резонансного захвата;
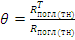 - коэффициент использования тепловых нейтронов;
- коэффициент использования тепловых нейтронов;
Rген(тн) - число быстрых нейтронов, генерируемых в единицу времени при делении ядер топлива тепловыми нейтронами; Rген - число быстрых нейтронов, генерируемых в единицу времени при делении ядер топлива нейтронами всех энергий; 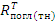 - число тепловых нейтронов, поглощаемых в топливе в единицу времени;
- число тепловых нейтронов, поглощаемых в топливе в единицу времени; 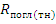 - число тепловых нейтронов, поглощаемых во всей размножающей среде в единицу времени;
- число тепловых нейтронов, поглощаемых во всей размножающей среде в единицу времени; 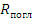 - число нейтронов всех энергий, поглощаемых во всей среде в единицу времени; -
- число нейтронов всех энергий, поглощаемых во всей среде в единицу времени; - 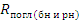 - число быстрых и резонансных нейтронов, поглощаемых в единицу времени во всей среде.
- число быстрых и резонансных нейтронов, поглощаемых в единицу времени во всей среде.
ЗАМЕДЛЕНИЕ НЕЙТРОНОВ
В реакторах на тепловых нейтронах для получения тепловых нейтронов используются замедлители — вещества с малым атомным весом.
Среде
Плотность замедления
Плотность замедления q ( E ) представляет собой число нейтронов в единице объема, энергия которых изменяется за единицу времени от значения выше Е до некоторой энергии ниже Е.
Эта функция характеризует скорость, с которой нейтроны, замедляясь, пересекают некоторую данную энергию Е. Можно представить себе функцию q по аналогии с потоком жидкости как скорость потока нейтронов, движущихся по энергетической шкале. Плотность замедления имеет одно и то же значение в любой шкале, если измерения производятся при соответствующих друг другу величинах Е, ν или и, т.е. q ( E )= q ( v )= q ( u ).
Рассмотрим бесконечную среду без поглощения нейтронов, в которую непрерывно и равномерно по всему пространству вводятся нейтроны с энергией E0 со скоростью S 0 нейтронов в единицу времени и в единицу объема. В этой среде устанавливается стационарное состояние и число нейтронов в любом данном энергетическом интервале ∆Е и данном объеме будет постоянным во времени. Все нейтроны, вводимые в среду с энергией E0, замедляются до некоторой энергии ниже Е, поэтому q ( E 0 )= S 0 .
В стационарном состоянии число нейтронов, попадающих при замедлении в данный интервал энергии, должно быть при отсутствии поглощения равно числу нейтронов, покидающих при замедлении этот интервал, то есть нейтроны не накапливаются ни при какой энергии и ни в какой промежуток времени. Таким образом, для E < E 0 :
q ( E + dE )= q ( E ) или 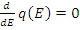 и q ( E )= const
и q ( E )= const
Если использовать начальное условие, то q ( E )= S 0 . Следовательно, плотность замедления, по этой модели, не зависит от энергии.
Определим соотношение между плотностью потока и плотностью замедления. R ( u ) du = ΣS ( u )Ф( u ) du - полное число рассеяний нейтронов, энергии которых кат в интервале du около и, отнесенных к единице объема и единице времени.
Эту же величину можно также получить с помощью плотности замедления q(u), т.е. R ( u ) du = q ( u ) 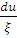 , где — есть среднее число рассеяний, выводящих нейтроны из интервала du . Приравняв эти выражения, получим q ( u )=ξΣ S ( u )Ф( u ) ( в случае бесконечной чисто рассеивающей среды).
, где — есть среднее число рассеяний, выводящих нейтроны из интервала du . Приравняв эти выражения, получим q ( u )=ξΣ S ( u )Ф( u ) ( в случае бесконечной чисто рассеивающей среды).
С учетом Ф(Е)dE=-Ф(u)du, 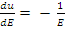 получим q ( E )= ξEES ( E )Ф( E ).
получим q ( E )= ξEES ( E )Ф( E ).
Спектр замедляющихся нейтронов в водородсодержащей среде без поглощения
Наиболее простая картина замедления нейтронов наблюдается в бесконечной гомогенной замедляющей среде, состоящей только из атомов водорода (ε=0, ξ=1), и в отсутствие поглощения нейтронов. В такой среде нейтрон после каждого столкновения сохраняется и с одинаковой вероятностью приобретает любую энергию меньше исходной. Хотя в процессе замедления нейтроны рассекаются по объему вещества, в случае равномерно распределенных источников по как угодно большому объему в любой единице объема число нейтронов с данной энергией будет одинаковым.
Для нахождения энергетического распределения нейтронов воспользуемся равнением баланса нейтронов в интервале энергии dE .
Число нейтронов, исчезающих из интервала dE в результате рассеяний, которые изменяют энергию нейтрона до величины, выходящей за пределы интервала, в стационарном состоянии равно числу нейтронов, которые попадают в от интервал в результате рассеяний из области энергии Е’>Е.
Так как Σа=0, то убыль нейтронов из интервала dE обусловлена только рассеянием нейтронов и равна скорости рассеяний в интервале dE — Σ S E)Ф(E)dE. Плотность потока замедляющихся нейтронов обычно относится к единичному энергетическому интервалу и является функцией энергии; [Ф(E)]=1/(см с эВ); Ф( E ) dE — плотность потока нейтронов, энергия которых лежит в интервале Е÷ E + dE .
Доля нейтронов с начальной энергией E '≤ E 0 , попадающих в результате столкновения с ядром в энергетический интервал dE , представляет собой отношение ширины этого интервала к полной ширине ступеньки замедления (1-ε)Е'. Для водорода ширина такой ступеньки равна Е' и указанная доля равна dE / E '.
Число столкновений в интервале dE ' при энергии Е' равно 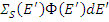 . Число нейтронов, попавших в dE из dE ', равно
. Число нейтронов, попавших в dE из dE ', равно 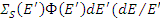 , а из всего интервала от E до E 0 равно
, а из всего интервала от E до E 0 равно 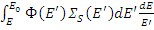 .
.
Число нейтронов, испытавших (после рождения от источника) первое рассеяние при энергии E 0 , равно S 0 . Число нейтронов, попавших в интервал dE после первого рассеяния, равно S 0 ( dE / E 0 ).
Уравнение баланса нейтронов:
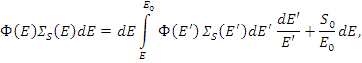
иначе
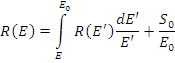
Продифференцировав уравнение по Е, получим
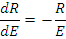
Решение уравнения есть
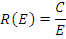
а константа С определяется подстановкой решения в интегральное уравнение при Е=Е0; C = S 0 .
Окончательное решение для среды из атомов водорода имеет вид
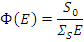
Спектр замедляющихся нейтронов в произвольной среде без поглощения
При замедлении в средах с ξ<1 при энергиях близких к E 0 , возникают особенности в распределении Ф(Е), однако при снижении Е особенности исчезают и распределение плотности потока описывается асимптотическим выражением
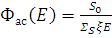 - спектр Ферми.
- спектр Ферми.
В промежуточной области 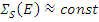 поэтому плотность потока замедляющихся нейтронов обратно пропорциональна энергии. Причина такого увеличения в том, что при замедлении уменьшается средняя потеря энергии на столкновение
поэтому плотность потока замедляющихся нейтронов обратно пропорциональна энергии. Причина такого увеличения в том, что при замедлении уменьшается средняя потеря энергии на столкновение 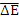 и, чтобы пройти единичный интервал энергии, требуется больше актов рассеяния.
и, чтобы пройти единичный интервал энергии, требуется больше актов рассеяния.
Плотность замедления в среде без поглощения постоянна и равна мощности источников:
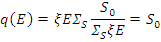
Спектр Ферми в шкале летаргии
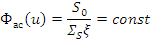
Если источник - нейтроны деления, спектр Ферми справедлив при u>5, для моноэнергетического — при любом и.
Спектр замедляющихся нейтронов в водородсодержащей среде с поглощением
Уравнение замедления при учете поглощения нейтронов усложняется. Допустим, что замедлитель - водород, а поглотителя мало:
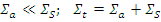
Уравнение баланса нейтронов
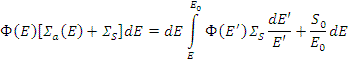
Дифференцируя данное уравнение, получим
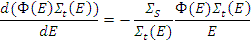
Решение этого уравнения
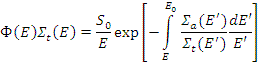
Спектр нейтронов можно записать в следующем виде:
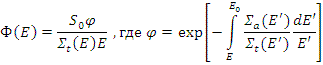
В выражении для плотности потока нейтронов появился дополнительный экспоненциальный множитель, меньший единицы. Этот же множитель появляется и в выражении для плотности замедления q ( E ), что означает, что до энергии Е доходят не все нейтроны, а только часть их, не поглотившаяся при более высоких энергиях.
Физический смысл коэффициента φ: это отношение числа нейтронов, достигших энергии Е при замедлении, к числу нейтронов, которые начали процесс замедления. Так как поглощение происходит в основном в резонансной области, то φ - вероятность избежать резонансного поглощения при замедлении нейтронов до энергии Е (произвольной энергии).
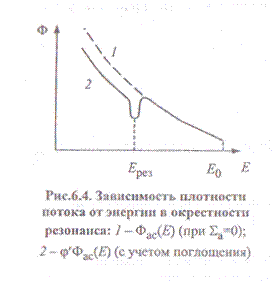 Сечение поглощения возрастает вблизи энергии каждого резонанса, соответственно возрастает полное сечение
Сечение поглощения возрастает вблизи энергии каждого резонанса, соответственно возрастает полное сечение 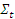 . Это обусловливает снижение плотности потока нейтронов (рис.6.4). После прохождения резонанса сечение
. Это обусловливает снижение плотности потока нейтронов (рис.6.4). После прохождения резонанса сечение 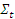 восстанавливается до
восстанавливается до 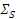 и соответственно восстанавливается плотность потока. Однако плотность потока составляет долю φ' от плотности потока без резонанса, если вероятность избежать резонансного поглощения в данном резонансе есть φ'.
и соответственно восстанавливается плотность потока. Однако плотность потока составляет долю φ' от плотности потока без резонанса, если вероятность избежать резонансного поглощения в данном резонансе есть φ'.
Выражение для плотности потока замедляющихся нейтронов при использовании летаргии
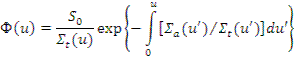
Если в среде без поглощения Ф(u)=const, то при наличии - гладкая функция, убывающая с возрастанием и.
Спектр замедляющихся нейтронов в произвольной среде с поглощением
Спектр нейтронов в такой среде записывается в виде
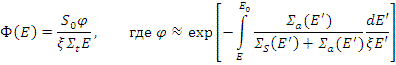
Если среда - смесь, то используется усредненная величина ξ( ξ → ξ).
Спектр нейтронов в реакторе
Замедляющиеся нейтроны распределены по энергетическому спектру, близкому к спектру Ферми. В результате замедления нейтроны становятся тепловыми. В реакторах на тепловых нейтронах плотность потока всех тепловых нейтронов и плотность потока нейтронов всех остальных энергий примерно равны. Соответственно концентрация тепловых нейтронов много больше, чем нетепловых.
Тепловые нейтроны при столкновениях с ядрами среды также теряют свою энергию либо приобретают - в зависимости от величины и направления скорости ядер-мишеней. При этом некоторая часть тепловых нейтронов будет иметь энергию, меньшую средней энергии теплового движения ядер среды, а другая часть — большую. Установление теплового равновесия между нейтронами и ядрами среды называется термализацией. Граница между областями замедления и термализации определяется, главным образом, температурой среды - при 300 К Eгр=0,2 эВ, при 1000К Егр=0,625 эВ.
Энергетическое распределение тепловых нейтронов в слабо поглощающих средах является распределением Максвелла:
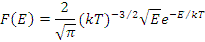
где 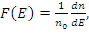 эВ-1 - доля тепловых нейтронов в единице объема в единичном энергетическом интервале, имеющих энергию Е; п0 - полное число тепловых нейтронов в единице объема; T—абсолютная температура среды;
эВ-1 - доля тепловых нейтронов в единице объема в единичном энергетическом интервале, имеющих энергию Е; п0 - полное число тепловых нейтронов в единице объема; T—абсолютная температура среды;
k=8,62 10-5 эВ/К - постоянная Больцмана.
 Данное распределение показано на рис.6.5. Средняя энергия спектра Максвелла равна (3/2) k Т, а энергия максимума распределения (наиболее вероятная энергия) — (1/2) k Т [5]. За стандартную тепловую энергию Ест принимают энергию k Т, что удобно, поскольку k Т— параметр распределения Максвелла. При
Данное распределение показано на рис.6.5. Средняя энергия спектра Максвелла равна (3/2) k Т, а энергия максимума распределения (наиболее вероятная энергия) — (1/2) k Т [5]. За стандартную тепловую энергию Ест принимают энергию k Т, что удобно, поскольку k Т— параметр распределения Максвелла. При
нормальной температуре T=TН=293 К (20° С) kT=0,025 эВ, что соответствует скорости нейтронов 2200 м/с. В таблицах сечений приводятся значения при стандартной энергии Ест при нормальной температуре.
Средняя энергия тепловых нейтронов оказывается несколько выше средней энергии теплового движения молекул среды. Это означает, что теплового равновесия нейтронов с молекулами среды не устанавливается. Причина заключается в поглощении нейтронов, а скорость поглощения выше при меньших скоростях нейтронов. Кроме того, происходит пополнение их числа со стороны более высоких энергий при замедлении. Тем не менее, распределение нейтронов близко спектру Максвелла, но соответствующему более высокой температуре, чем температура среды. Эта температура нейтронного газа ТНГ равна:
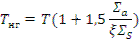
где 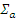 — макроскопическое сечение поглощения тепловых нейтронов при энергии k Т;
— макроскопическое сечение поглощения тепловых нейтронов при энергии k Т; 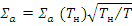 ;
; 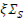 - замедляющая способность среды с энергией 1 эВ [7].
- замедляющая способность среды с энергией 1 эВ [7].
Уравнение диффузии
Уравнение диффузии определяет баланс нейтронов в единичном объёме, рассматриваются моноэнергетические нейтроны - ν=const, но Ф=nν≠const
Рассмотрим баланс нейтронов в элементарном объеме dV : изменение числа нейтронов в единицу времени = = скорость генерации — скорость поглощения - скорость утечки. Изменение числа нейтронов в единицу времени в единице объема 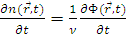 , изменение числа нейтронов в единицу времени в элементарном объеме
, изменение числа нейтронов в единицу времени в элементарном объеме 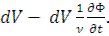
Скорость генерации нейтронов в единице объема - 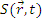 , скорость генерации в объеме dV — SdV .
, скорость генерации в объеме dV — SdV .
Скорость поглощения нейтронов в единице объема - 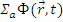 ,скорость поглощения в объеме dV — ΣaФdV .
,скорость поглощения в объеме dV — ΣaФdV .
Под утечкой понимается разность чисел нейтронов, вылетающих и влетающих через поверхность, ограничивающую рассматриваемый элемент объема (рис.7.3). Рассмотрим элемент объема dV , имеющий вид куба со сторонами dx , dy , dz ; Jz - плотность результирующего тока нейтронов, входящих в dV через нижнюю грань; Jz + dz - плотность результирующего тока нейтронов, выходящих из dV через верхнюю грань. Скорость утечки из dV в направлений оси z:
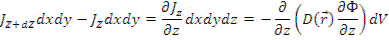
Полная скорость утечки нейтронов из объема dV:
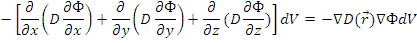
а для однородной среды - -D ∆ФdV ,
где 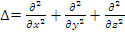 - оператор Лапласа.
- оператор Лапласа.
Нестационарное уравнение диффузии:
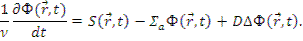
Это нестационарное уравнение в частных производных второго порядка.
Стационарное уравнение диффузии:
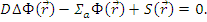
 Уравнение диффузии справедливо, если угловое распределение плотности потока нейтронов близко к изотропному, при котором число нейтронов в данном элементе объема, движущихся в любом направлении, одинаково. Уравнение диффузии достаточно точно описывает пространственное распределение нейтронов в слабопоглощающих средах, вдали от источников и границ раздела сред с различными свойствами или с резкой зависимостью сечений от координат. Примерами сред, в которых реальные пространственные распределения нейтронов совпадают с решениями уравнения диффузии, являются большие объемы чистого замедлителя. Вблизи сильного поглотителя или источника нейтронов, вблизи границы тела с пустотой (воздухом) распределение плотности потокa неизотропно, поскольку число нейтронов, движущихся в сторону поглотителя, от источника, в сторону пустоты, всегда больше, чем число нейтронов, движущихся в противоположном направлении. Но если объем областей с нарушениями изотропии диффузии мал относительно объема тела, то могут быть едены такие поправки к решениям уравнения диффузии, которые делают эти решения применимыми во многих практически важных случаях.
Уравнение диффузии справедливо, если угловое распределение плотности потока нейтронов близко к изотропному, при котором число нейтронов в данном элементе объема, движущихся в любом направлении, одинаково. Уравнение диффузии достаточно точно описывает пространственное распределение нейтронов в слабопоглощающих средах, вдали от источников и границ раздела сред с различными свойствами или с резкой зависимостью сечений от координат. Примерами сред, в которых реальные пространственные распределения нейтронов совпадают с решениями уравнения диффузии, являются большие объемы чистого замедлителя. Вблизи сильного поглотителя или источника нейтронов, вблизи границы тела с пустотой (воздухом) распределение плотности потокa неизотропно, поскольку число нейтронов, движущихся в сторону поглотителя, от источника, в сторону пустоты, всегда больше, чем число нейтронов, движущихся в противоположном направлении. Но если объем областей с нарушениями изотропии диффузии мал относительно объема тела, то могут быть едены такие поправки к решениям уравнения диффузии, которые делают эти решения применимыми во многих практически важных случаях.
Граничные условия
Общее решение уравнения второго порядка содержит две произвольные постоянные. Константы определяются из граничных условий по заданным значениям функции в граничных точках, или исходя из условий симметрии задачи, или исходя из требования конечности и неотрицательности функции плотности потока нейтронов во всей области изменения переменных (последнее вытекает из физического смысла плотности потока Ф). Для единственности решения любой конкретной задачи необходимо иметь два граничных условия. Для решения нестационарной задачи необходимо и начальное условие.
Граничные условия на плоской границе двух сред:
1) плотности потоков равны;
2) плотности результирующих токов по нормали равны.
Доказательство
Если на границе нет источников, то число нейтронов, пересекающих единичную площадку 1 в направлении слева направо (справа налево), равно числу нейтронов, прошедших площадку 2 в том же направлении (рис.7.4), т.е. односторонние токи должны быть непрерывны:
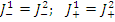
 С учетом ранее полученных формул для J _ и J + имеем: - плотности односторонних токов в направлении против оси x (J_):
С учетом ранее полученных формул для J _ и J + имеем: - плотности односторонних токов в направлении против оси x (J_):
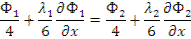
плотности односторонних токов в направлении оси х ( J + ):
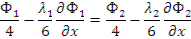
Складываем данные выражения, тогда – Ф1=Ф2 (первое условие).
Вычитаем, тогда- 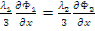 или
или 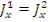 (второе условие).
(второе условие).
Альбедо
Альбедо - это отражающая способность или коэффициент отражения (понятие, заимствованное из оптики).
Альбедо нейтронов 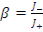 где J + , J_ - плотности односторонних токов
где J + , J_ - плотности односторонних токов
нейтронов на входе и выходе в отражатель соответственно. Для плоской границы:
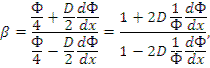
где 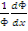 значение на границе.
значение на границе.
Значения альбедо определяются диффузионными константами среды и близостью границы отражателя с пустотой. Нейтроны отражаются не от плоскостей, а от объемов вещества. Если толщина отражателя мала по сравнению с длиной диффузии, то многие нейтроны достигают границы с пустотой и покидают объем тела. Поэтому уменьшение толщины отражателя снижает альбедо.
Альбедо отражателя конечной толщины а (плоская граница):
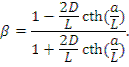
Значения альбедо бесконечной среды велики. В табл.7.1 приведены значения альбедо различных сред. Когда a >2 L , отражатель можно считать бесконечным. В таком случае альбедо зависит только от диффузионных констант среды. Альбедо отражателя бесконечной толщины (плоская граница):
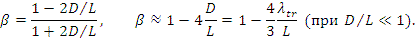
При увеличении L возрастает β. При увеличении 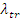 уменьшается β. Длина диффузии L характеризует сохранность нейтронов, транспортная длина
уменьшается β. Длина диффузии L характеризует сохранность нейтронов, транспортная длина 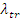 -глубину проникновения нейтронов в отражатель (расстояние, на котором траектория нейтронов поворачивается на угол π/2).
-глубину проникновения нейтронов в отражатель (расстояние, на котором траектория нейтронов поворачивается на угол π/2).
Благодаря высоким коэффициентам отражения, каждый нейтрон в процессе диффузии многократно пересекает некоторую условную плоскость внутри объема тела. Соседние объемы вещества много раз обмениваются одними и теми же порциями нейтронов, что создает высокие концентрации нейтронов в конденсированных средах, которые наблюдаются на опыте и в сравнении с которыми концентрации в направленных нейтронных потоках в пустом пространстве пренебрежимо малы. По той же причине диффузионный ток 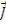 обычно мал в сравнении со скалярным потоком Ф.
обычно мал в сравнении со скалярным потоком Ф.
Начальные условия
Точечный источник мощностью S расположен в точке 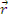 = 0:
= 0:
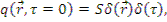
где 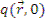 - число нейтронов в единице объема в единицу времени, начинающих замедление; δ - дельта-функция Дирака, т.е. плотность замедления нейтронов с τ=0 в точке
- число нейтронов в единице объема в единицу времени, начинающих замедление; δ - дельта-функция Дирака, т.е. плотность замедления нейтронов с τ=0 в точке 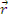 = 0 равна мощности источника S в данной точке (
= 0 равна мощности источника S в данной точке ( 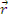 = 0 ) - предполагается, что все нейтроны рождаются с одной и той же энергией и возраст нейтронов источника равен нулю.
= 0 ) - предполагается, что все нейтроны рождаются с одной и той же энергией и возраст нейтронов источника равен нулю.
Точечный источник мощностью S расположен в точке 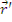 :
:
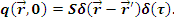
Распределенный источник:
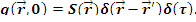
где 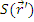 - мощность источника в точке
- мощность источника в точке 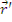 .
.
Граничные условия
Граничные условия, полученные ранее для диффузии моноэнергетических нейтронов, справедливы и для диффузии замедляющихся нейтронов.
1. Условия на границе, разделяющей две среды: должны быть непрерывны плотность потока и первая производная (градиент) потока, умноженная на коэффициент диффузии в среде:
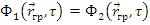
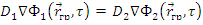
Переходя от плотности потока Ф к плотности замедления q , получим
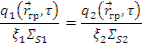
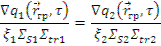
2. Условие на внешней поверхности среды (границе тела с вакуумом)
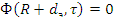
Граничные условия должны выполняться для всего спектра энергий нейтронов.
Условия применимости уравнения возраста:
1. Справедливо диффузионное приближение.
2. Тяжелый замедлитель, для которого справедлива модель непрерывного замедления ( 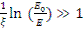 , т.е. бесконечно много соударений до того, как летаргия
, т.е. бесконечно много соударений до того, как летаргия
станет равной и).
Решения уравнения возраста в простейших случаях
Уравнение возраста решается с помощью преобразований Фурье. Решение для точечного источника
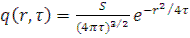 (8.5)
(8.5)
Следовательно, плотность замедления описывается распределением Гаусса.
Если τ мало, т.е. велика энергия, то нейтроны находятся вблизи точечного источника (рис.8.2). С ростом τ по мере замедления пространственное распределение всё больше расплывается. Наконец, при достижении тепловой энергии последняя зависимость дает распределение источников тепловых нейтронов 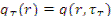 около точечного источника быстрых нейтронов.
около точечного источника быстрых нейтронов.
Обобщенная формула для плоского, линейного, точечного источников:
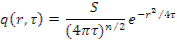
 Для плоского источника п=1, тогда S-число нейтронов, испускаемых единицей поверхности источника. Для линейного источника n=2, тогда S - число нейтронов, испускаемых единицей длины. Для сферического (точечного) источника п=3.
Для плоского источника п=1, тогда S-число нейтронов, испускаемых единицей поверхности источника. Для линейного источника n=2, тогда S - число нейтронов, испускаемых единицей длины. Для сферического (точечного) источника п=3.
В случае непрерывного расположения источников выражение для плотности замедления можно записать, используя принцип суперпозиции источников, в виде
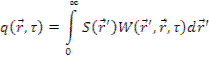
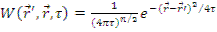 — функция влияния для замедляющихся нейтронов (функция Грина). Функция влияния представляет собой вероятность того, что быстрый нейтрон, рожденный в точке
— функция влияния для замедляющихся нейтронов (функция Грина). Функция влияния представляет собой вероятность того, что быстрый нейтрон, рожденный в точке 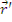 , будет иметь возраст τ в точке
, будет иметь возраст τ в точке 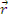 .
.
Возраст нейтронов
Используя решение для случая точечного источника, можно определить средний квадрат смещения нейтронов от источника при замедлении нейтронов до энергии, соответствующей возрасту τ:
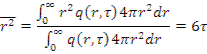
где q - плотность замедления для точечного источника (поглощение отсутствует, рассеяние упругое).
Тогда 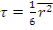 , т.е. возраст тепловых нейтронов равен 1/6 среднего квадрата
, т.е. возраст тепловых нейтронов равен 1/6 среднего квадрата
смещения нейтрона от точечного источника (от точки рождения) до точки, где его энергия в процессе замедления стала тепловой.
При этом 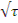 — длина замедления.
— длина замедления.
В табл.8.1 приведены экспериментальные значения возраста тепловых нейтронов от источника нейтронов деления при нормальных условиях [3].
 Утечка замедляющихся нейтронов из объема тела будет небольшой, если выполняется условие
Утечка замедляющихся нейтронов из объема тела будет небольшой, если выполняется условие 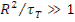 , где R — характерный размер тела. В энергетических реакторах достаточно, чтобы
, где R — характерный размер тела. В энергетических реакторах достаточно, чтобы 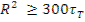 .
.
Возраст тепловых нейтронов τт и квадрат длины диффузии L описывают смещение нейтронов в пространстве соответственно при замедлении и диффузии в тепловой области и составляют квадрат длины миграции (площадь миграции):
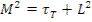
Площадь миграции равна 1/6 среднего квадрата смещения нейтрона от точки рождения до точки его поглощения. При этом 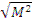 - длина миграции.
- длина миграции.
Теория возраста дает тем лучшее согласие с опытом, чем тяжелее вещество-замедлитель и соответственно меньше ξ, т.е. чем ближе механизм потерь энергии к модели непрерывного замедления и больше число столкновений при замедлении. Поэтому в водородсодержащих средах теория возраста неприменима. Это связано в первую очередь с большой величиной ξ. Большая часть смещения нейтронов в водородсодержащих средах связана с несколькими первыми столкновениями, а теория возраста неприменима к случаю малого числа столкновений. Поэтому распределение (8.5) не имеет места в таких средах. Однако по аналогии с другими замедлителями величина 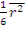 называется возрастом и в водородсодержащих средах.
называется возрастом и в водородсодержащих средах.
Время замедления
Из зависимости (8.1) между хронологическим временем замедляющегося нейтрона и его энергии 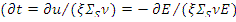 можно найти время замедления до тепловой энергии [5]:
можно найти время замедления до тепловой энергии [5]:
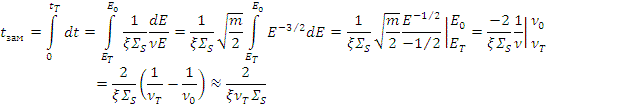
где 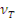 =2,2 103 м/с и
=2,2 103 м/с и 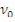 =2 107 м/с - скорости теплового нейтрона и нейтрона деления соответственно;
=2 107 м/с - скорости теплового нейтрона и нейтрона деления соответственно; 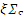 усреднено по интервалу замедления.
усреднено по интервалу замедления.
 В табл.8.2 приведены время замедления в замедлителях от E 0 =2 МэВ до
В табл.8.2 приведены время замедления в замедлителях от E 0 =2 МэВ до
Eт=0,025 эВ и время диффузии в тепловой
области 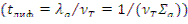 [3]. Время диффузии примерно в 100 раз больше, чем время замедления. В ядерных реакторах на тепловых нейтронах, благодаря наличию урана, поглощающего нейтроны, время диффузии уменьшается. Однако оно составляет ~10-3 с в реакторах с графитовым и тяжеловодным замедлителем и ~10-4 с в
[3]. Время диффузии примерно в 100 раз больше, чем время замедления. В ядерных реакторах на тепловых нейтронах, благодаря наличию урана, поглощающего нейтроны, время диффузии уменьшается. Однако оно составляет ~10-3 с в реакторах с графитовым и тяжеловодным замедлителем и ~10-4 с в
реакторах с обычной водой, что всё равно много больше времени замедления. В реакторах на быстрых нейтронах замедления практически нет и полное время жизни нейтрона очень мало - около 10-7 с. Хотя сечения поглощения в области энергии быстрых нейтронов невелики, и нейтрон до поглощения испытывает много столкновений с ядрами атомов среды, благодаря скорости порядка 107 м/с это происходит за очень малое время.
Влияние отражателя
Добавление к поверхности активной зоны слоя материала (отражателя) при-
водит к тому, что часть нейтронов, выходящих из активной зоны, возвращается
обратно. Доля отражающихся нейтронов определяется величиной альбедо отражателя. При этом уменьшается утечка нейтронов из активной зоны. Если без
отражателя реактор - критический, то с отражателем он будет надкритическим.
Чтобы реактор с отражателем оставался критическим, надо уменьшить размеры
активной зоны. Поэтому критические размеры активной зоны реактора с отражателем всегда меньше, чем соответствующие размеры без отражателя.
Распределение нейтронов у границы раздела формируется перетечками из
одной среды в другую. Вблизи границы нарушается пропорциональность потоков быстрых и тепловых нейтронов, поскольку отражателями служат, как правило, материалы с малым сечением поглощения нейтронов и иными, чем в активной зоне, диффузионными свойствами. При этом переменные r и Е в функции Ф(r,E) не разделяются.
По мере удаления от границы в глубину активной зоны влияние отражателя
уменьшается и распределение нейтронов по пространству и энергии приближается к форме, зависящей только от параметров активной зоны. Такое распределение называется асимптотическим.
Пространственно-энергетическое распределение нейтронов в реакторе с отражателем определяется приближенно: диапазон энергий нейтронов разбивается на несколько интервалов, рассматривается диффузия каждой группы ней-
тронов с неизменной энергией - средней энергией в пределах каждого интервала. При этом решается система уравнений, в которой плотность потока нейтронов зависит только от пространственной переменной.
Для иллюстрации многих свойств реакторов с отражателем и оценки масштаба эффектов отражателя используются одногрупповое и двухгрупповое.
Материалы отражателей
Отражатели реакторов на тепловых и промежуточных нейтронах изготавливаются из веществ-замедлителей. Такие отражатели слабо поглощают нейтроны и способствуют их замедлению в реакторе.
В графитовых и тяжеловодных реакторах (на тепловых нейтронах) в качестве отражателя применяется графит как наиболее доступный материал с хорошими диффузионными свойствами. В легководных реакторах отражателем является слой воды в 10 см или более, располагающийся между активной зоной и корпусом реактора. Такие реакторы не имеют отражателя как отдельной конструкции.
В реакторах на промежуточных нейтронах в качестве отражателя применяется бериллий. Реакторы на промежуточных нейтронах содержат мало замедлителя и нейтроны поглощаются прежде, чем становятся тепловыми. Активные зоны таких реакторов рассеивают быстрые и промежуточные нейтроны. Бериллий является наилучшим отражателем, поскольку имеет в области быстрых нейтронов самую низкую величину 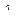 , благодаря достаточно большой величине σtr и высокой концентрации атомов.
, благодаря достаточно большой величине σtr и высокой концентрации атомов.
В реакторах на быстрых нейтронах в качестве отражателя применяются материалы из тяжелых элементов – U238 или Th232 Реакторы на быстрых нейтронах не должны содержать вещества, замедляющие нейтроны, так как замедление снижает коэффициент воспроизводства новых делящихся материалов. Изотопы U238 и Th232 являются одновременно сырьем для Pu239 и U233 соответственно, что является их основной функцией.
Период реактора
Время, в течение которого величина плотности нейтронного потока (или нейтронной плотности) изменяется в е раз, называется периодом реактора и обозначается через Т. Величину Т можно определить математически, если положить:
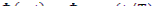 (12.11)
(12.11)
Сравнение этого выражения с формулой (12.10) показывает, что в рассматриваемом случае (т.е. предполагая, что при делении возникают только мгновенные нейтроны)
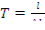 (12.12)
(12.12)
Согласно приведенному ранее анализу, если реактор находится в нестационарном состоянии ( 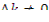 ), плотность потока тепловых нейтронов возрастает (или убывает) экспоненциально, причем показатель экспоненты определяется отношением среднего времени жизни теплового нейтрона к коэффициенту избыточного размножения. Этот результат не является неожиданным, он может быть также получен из общих соображений, приведенных в гл. 5. Действительно, если пренебречь временем замедления, то легко видеть, что среднее время жизни теплового нейтрона по существу есть время жизни одного поколения нейтронов, а следовательно, полученная в гл. 5 зависимость для плотности нейтронов от времени эквивалентна формуле (12.10). Период реактора оказывается, таким образом, равным времени жизни одного поколения нейтронов, деленному на фактор избыточного размножения. Следует отметить, что полученный результат является совершенно общим, он справедлив как для мгновенных, так и для запаздывающих нейтронов. Однако следует подчеркнуть, что, среднее время жизни теплового нейтрона можно отождествлять с временем жизни одного поколения нейтронов только в том случае, когда все рождающиеся в процессе деления нейтроны являются мгновенными.
), плотность потока тепловых нейтронов возрастает (или убывает) экспоненциально, причем показатель экспоненты определяется отношением среднего времени жизни теплового нейтрона к коэффициенту избыточного размножения. Этот результат не является неожиданным, он может быть также получен из общих соображений, приведенных в гл. 5. Действительно, если пренебречь временем замедления, то легко видеть, что среднее время жизни теплового нейтрона по существу есть время жизни одного поколения нейтронов, а следовательно, полученная в гл. 5 зависимость для плотности нейтронов от времени эквивалентна формуле (12.10). Период реактора оказывается, таким образом, равным времени жизни одного поколения нейтронов, деленному на фактор избыточного размножения. Следует отметить, что полученный результат является совершенно общим, он справедлив как для мгновенных, так и для запаздывающих нейтронов. Однако следует подчеркнуть, что, среднее время жизни теплового нейтрона можно отождествлять с временем жизни одного поколения нейтронов только в том случае, когда все рождающиеся в процессе деления нейтроны являются мгновенными.
Как указывалось ранее, если реактор находится в надкритическом состоянии, kэфф >1 и 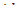 положительно. Отсюда следует, что и период реактора есть величина положительная. Это означает, что в надкритическом состоянии плотность потока нейтронов в реакторе возрастает с течением времени по экспоненте в соответствии с формулой (12.10). Наоборот, в реакторе, находящемся в подкритическом состоянии, период, так же, как и
положительно. Отсюда следует, что и период реактора есть величина положительная. Это означает, что в надкритическом состоянии плотность потока нейтронов в реакторе возрастает с течением времени по экспоненте в соответствии с формулой (12.10). Наоборот, в реакторе, находящемся в подкритическом состоянии, период, так же, как и 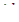 , отрицателен и плотность потока нейтронов экспоненциально убывает.
, отрицателен и плотность потока нейтронов экспоненциально убывает.
Если эффективный коэффициент размножения скачкообразно увеличится на 0,01, т.е. 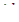 =0,01, то период большого реактора на тепловых нейтронах l≈0,001 с, согласно формуле (12.12), равен (0,001/0,01) с, т.е. 0,1 с. Следовательно, в течение каждой десятой доли секунды плотность нейтронного потока будет увеличиваться в е раз.
=0,01, то период большого реактора на тепловых нейтронах l≈0,001 с, согласно формуле (12.12), равен (0,001/0,01) с, т.е. 0,1 с. Следовательно, в течение каждой десятой доли секунды плотность нейтронного потока будет увеличиваться в е раз.
СПИСОК ЛИТЕРАТУРЫ
1. Галаиин, А.Д. Введение в теорию ядерных реакторов на тепловых нейтронах: учеб. пособие для вузов / А.Д. Галанин. - М.: Энергоатомиздат, 1984.
-416с.
2. Глесстон, С. Основы теории ядерных реакторов: [пер. с англ.] / С. Глесстон, М. Эдлунд. - М.: Изд-во иностранной лит-ры, 1954. - 458 с.
3. Гордеев,И.В. Ядерно-физические константы: справочник / И.В.Гордеев, Д.А. Кардашев, А.В. Малышев. - М.: Госатомиздат, 1963. - 507 с.
4. Дементьев, Б.А. Кинетика и регулирование ядерных реакторов: учеб. пособие / Б.А. Дементьев. - М.: Атомиздат, 1973. - 292 с.
5. Климов, А.Н. Ядерная физика и ядерные реакторы: учеб. для вузов / А.Н. Климов. - М.: Энергоатомиздат, 1985. - 352 с.
6. Мегреблиан, Р. Теория реакторов / Р. Мегреблиан, Д. Холмс. - М.: Госатомиздат, 1962. - 590 с.
7. Основы теории и метода расчета ядерных энергетических реакторов: учеб. пособие для вузов / Г.Г. Бартоломей, Г.А. Бать [и др.]. - М.: Энергоатомиздат, 1989.-512 с.
ВЛАСИЧЕВ ГЕРМАН НИКОЛАЕВИЧ
ФИЗИКА ЯДЕРНЫХ РЕАКТОРОВ
Редактор Е.В. Комарова
Технический редактор Т.П. Новикова
Компьютерный набор и верстка Г.Н. Власичев
Подписано в печать 10.11.2008. Формат 60 х 84 716. Бумага офсетная. Печать офсетная. Усл. печ. л. 6,75. Уч.-изд. л. 6,0. Тираж 500 экз. Заказ 731.
Нижегородский государственный технический университет им. Р.Е. Алексеева.
Типография НГТУ.Адрес университета и полиграфического предприятия: 603950, Н.Новгород, ул. Минина, 24.
[1] Цыб, А. Новые лечебные технологии в МРНЦ РАМН / А. Цыб, Б. Бердов // Ядерное общество.-2005.-С.70-71.
Власичев Г.Н.
В 58 Физика ядерных реакторов: учеб. пособие / Г.Н. Власичев; Нижего-род. гос. техн. ун-т им. Р.Е. Алексеева. Нижний Новгород, 2008. - 106 с. ISBN 978-5-93272-596-2
Рассмотрены физические основы теории ядерных реакторов, являющихся аппаратами для получения ядерной энергии, производства новых изотопов, а также пучков нейтронов, находящих в последние годы применение в клинической медицине. Изложены общие сведения о ядерных реакторах, взаимодействии нейтронов различных энергий с ядрами, цепной реакции деления, даны основы теории замедления и диффузии нейтронов, методики расчета коэффициента размножения нейтронов и критических размеров реактора, приведены основы кинетики.
Предназначено для студентов старших курсов специальностей 200402, 140101, 140404, обучающихся в институте ядерной энергетики и технической физики (ИЯЭиТФ), а также может быть полезно студентам специальности 140305.
Рис. 46. Табл. 16. Библиогр.: 7 назв.
УДК 621.039.5
ББК 31.46
ISBN 978-5-93272-596-2
© Нижегородский государственный
технический университет
им. Р.Е. Алексеева, 2008
© Власичев Г.Н., 2008
ОГЛАВЛЕНИЕ
| ВВЕДЕНИЕ | 5 |
| I. ОБЩИЕ СВЕДЕНИЯ О ЯДЕРНЫХ РЕАКТОРАХ | 6 |
| 1.1. Ядерный реактор как источник энергии | 6 |
| 1.2. Основные составные части реактора и их назначение | 7 |
| 1.3. Классификация реакторов по различным признакам | 7 |
| 2. ПАРАМЕТРЫ И ВИДЫ ВЗАИМОДЕЙСТВИЯ НЕЙТРОНОВ С ЯДРАМИ | 9 |
| 2.1. Понятие микроскопического сечения | 9 |
| 2.2. Понятия плотности потока нейтронов и макроскопического сечения | 10 |
| 2.3. Виды взаимодействия нейтронов с ядрами. | 11 |
| 3. ВЗАИМОДЕЙСТВИЕ НЕЙТРОНОВ РАЗЛИЧНЫХ ЭНЕРГИЙ С ЯДРАМИ | 13 |
| 3.1. Быстрые нейтроны | 13 |
| 3.2. Промежуточные (резонансные) нейтроны | 15 |
| 3.3. Медленные нейтроны | 19 |
| 3.4. Основные закономерности взаимодействия нейтронов с ядрами | 20 |
| 4. ПРОЦЕСС ДЕЛЕНИЯ И ПАРАМЕТРЫ, ЕГО ОПРЕДЕЛЯЮЩИЕ | 22 |
| 5. ЦЕПНАЯ РЕАКЦИЯ ДЕЛЕНИЯ | 27 |
| 6. ЗАМЕДЛЕНИЕ НЕЙТРОНОВ | 33 |
| 6.1. Характеристики замедления нейтронов | 33 |
| 6.2. Спектр замедляющихся нейтронов в бесконечной среде | 38 |
| 6.3. Спектр нейтронов в реакторе | 42 |
| 7. ДИФФУЗИЯ МОНОЭНЕРГЕТИЧЕСКИХ НЕЙТРОНОВ В ОДНОРОДНОЙ СРЕДЕ | 44 |
| 7.1. Характеристики диффузии нейтронов | 44 |
| 7.2. Плотность тока нейтронов, закон Фика | 45 |
| 7.3. Уравнение диффузии | 47 |
| 7.4. Альбедо | 54 |
| 8. ДИФФУЗИЯ ЗАМЕДЛЯЮЩИХСЯ НЕЙТРОНОВ | 55 |
| 9. КОЭФФИЦИЕНТ РАЗМНОЖЕНИЯ НЕЙТРОНОВ В БЕСКОНЕЧНОЙ СРЕДЕ | 61 |
| 9.1. Число нейтронов на акт поглощения | 61 |
| 9.2. Коэффициент размножения на быстрых нейтронах | 62 |
| 9.3. Вероятность избежать резонансного захвата | 62 |
| 9.4. Коэффициент использования тепловых нейтронов | 67 |
| 9.5. Усреднение сечений в области тепловых нейтронов | 69 |
| 9.6. Оптимальные параметры размножающих сред | 69 |
| 9.7. Длина диффузии и возраст нейтронов в размножающей среде | 70 |
| 10. КРИТИЧЕСКИЕ РАЗМЕРЫ ГОМОГЕННОГО РЕАКТОРА БЕЗ ОТРАЖАТЕЛЯ | 72 |
| 11. КРИТИЧЕСКИЕ РАЗМЕРЫ ГОМОГЕННОГО РЕАКТОРА С ОТРАЖАТЕЛЕМ | 81 |
| 12. НЕСТАЦИОНАРНЫЙ РЕЖИМ РЕАКТОРА БЕЗ ОТРАЖАТЕЛЯ | 85 |
| 12.1. Нестационарное уравнение диффузии | 85 |
| 12.2. Период реактора | 88 |
| 12.3. Учет запаздывающих нейтронов | 89 |
| 12.4. Кинетика реактора с учетом запаздывающих нейтронов | 90 |
| 12.5. Решение уравнений кинетики с учетом шести групп запаздывающих нейтронов | 93 |
| 12.6. Зависимость установившегося периода реактора от величины скачка реактивности | 95 |
| 12.7. Решение уравнений кинетики с учетом одной группы запаздывающих нейтронов | 97 |
| 12.8. Кинетика реактора при отрицательном скачке реактивности | 103 |
| СПИСОК ЛИТЕРАТУРЫ | 105 |
ВВЕДЕНИЕ
Ядерные реакторы в настоящее время применяются преимущественно для получения ядерной энергии - выработки электроэнергии, энергообеспечения и движения военных кораблей и гражданских судов. Перспективно получение тепловой энергии для коммунального хозяйства, использование высокотемпературного тепла для получения водорода, а также в металлургических процессах и других производствах. Ядерные реакторы находят применение в производстве делящихся материалов и радиоактивных изотопов для нужд обороны, промышленности, науки, медицины и других отраслей. Студенты, обучающиеся в институте ядерной энергетики и технической физики, должны иметь представление об устройстве ядерного реактора и об основных физических процессах, происходящих в реакторе.
На достижениях ядерной энергетики базируется медицинская радиология - молодая наукоемкая дисциплина, без которой сегодня не может обойтись ни один раздел клинической медицины. Существуют методики лучевой терапии с использованием протонов, нейтронов, электронов, фотонов, испускаемых радиоизотопами, получаемыми на ускорителях, а также в ядерных реакторах. В лучевой терапии нуждаются многие больные с опухолями. Выделим некоторые из лечебных технологий, в основу которых положены последние достижения в атомной энергетике: новый высокоэффективный метод сочетанной гамма-нейтронной терапии с использованием быстрых реакторных нейтронов на базе ( г. Обнинск); разрабатываемый медицинский блок на реакторе ВВРц НИВХИ им. Карпова ( г. Обнинск) для нейтронной и нейтрон-захватной терапии[1].
Учебное пособие посвящено физическим основам теории ядерных реакторов. Изложены общие сведения о ядерных реакторах, взаимодействии нейтронов различных энергий с ядрами, цепной реакции деления, даны основы теории замедления и диффузии нейтронов, методики расчета коэффициента размножения нейтронов и критических размеров реактора, приведены основы кинетики.
ОБЩИЕ СВЕДЕНИЯ О ЯДЕРНЫХ РЕАКТОРАХ
Дата: 2019-04-23, просмотров: 482.