Предполагаем, что диффузионная среда ограничена некой поверхностью, отделяющей эту среду от вакуума или от сильно поглощающего нейтроны тела.

Вблизи границы с пустотой на нево­гнутой поверхности поток изменяется так, что его линейная экстраполяция приводит поток к нулю на некотором расстоянии d _э от границы - Ф( R + d _э )=0 (рис.7.5), где d _э - длина линейной экст­раполяции. Это вытекает из следующих рассуждений.

Вакуум обладает тем свойством, что попавший в него нейтрон никогда не возвращается в среду, т.е. J _( x = R )=0.

Если предположить, что рассматри­ваемая теория диффузии справедлива

вплоть до границы, то

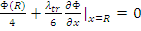
Экстраполируем кривую потока с наклоном 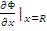  за границу и тогда из последней формулы найдем расстояние d _э :

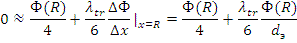
откуда d _э =2/3 λ_tr .

Решение, полученное при использовании уравнения диффузии, становится весьма грубым вблизи границы раздела (на расстоянии порядка λ_tr ). Более строгое рассмотрение данной задачи может быть основано на рассмотрении ин­тегрального уравнения Пайерлса [7]:

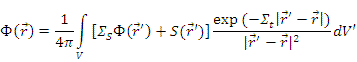
Уравнение Пайерлса может быть распространено и на случай неизотропного рассеяния в лабораторной системе координат, при этом Σ _S заменяется на Σ_Str . Оно справедливо как угодно близко к границам объема V .

Как частный случай из этого уравнения может быть получено уравнение диффузии при следующих предположениях: 1) плотность потока 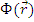 слабо меняется на длине свободного пробега; 2) скорость генерации нейтронов S сла­бо зависит от координат; 3) вдали от границ среды ( ).

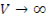Из рассмотрения интегрального уравнения длина линейной экстраполяции d_э =0,71λ_{tr .} Это значение принимают при использовании уравнения диффузии.

Поток нейтронов на экстраполированной границе в действительности не равен нулю. Введение экстраполированной границы, на которой поток нейтронов обращается в нуль, это лишь формальный математический прием, используе­мый при решении уравнения диффузии.

Простейшие решения стационарного уравнения диффузии в неразмножающей среде

Стационарное уравнение диффузии в объеме однородной среды, где нет ис­точников (S=0):

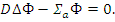
В данном уравнении Σ_a=const, D=const. Уравнение можно переписать в виде:

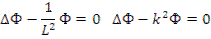
где L ² = D / Σ_a ; k ² =Σ _a / D ; k, L — параметры, определяющие свойства среды;

L - длина диффузии.

1. Точечный изотропный источник в бесконечной среде:

S ( r =0)= S ₀ (н/с).

Уравнение диффузии удобно записать в форме (для r≠0):

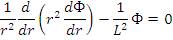
Граничные условия:

1) поток нейтронов ограничен;

2) полное число нейтронов, поглощаемых в единицу времени, равно скорости их генерации (условие баланса для стационарной задачи):

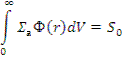
Уравнение диффузии решается методом замены переменных - Ф=и/ r . Общее решение:

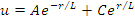
 где С=0, согласно первому условию (физическому смыслу Ф); константа А на­ходится из второго условия (нормировки на источник).

Формула для плотности потока нейтронов от точечного источника:

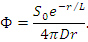
2. Плоский (бесконечный) источник в бесконечной среде:

S(х=0)=S₀ (н/см²с). Уравнение диффузии (для x ≠0):

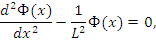
где х - расстояние от плоскости.

Формула для плотности потока нейтронов от плоского источника:

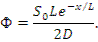
Согласно данному решению, L - длина релаксации нейтронов от плоского изотропного источника (длина, на которой плотность потока уменьшается в е раз).

3. Точечный источник в конечной однородной сфере радиусом R :

S ( r = 0 )= S ₀ (н/с).

Уравнение диффузии (для r≠0):

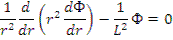
Граничные условия:

1) поток нейтронов равен нулю на экстраполированной границе сферы R_э;

2) ток нейтронов, проходящих через сферу радиусом r→0, равен скорости гене­рации нейтронов источником:

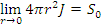
Формула для плотности потока нейтронов от точечного источника в конеч­ной сфере:

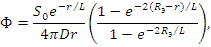
где R _э = R + d _э . Второй сомножитель ускоряет спад плотности потока нейтронов в конечном объеме по сравнению с бесконечным.

4. Произвольное распределение источников:

На основании решения для случая точечного источника, можно определить плотность потока нейтронов для произвольного распределения источников, ис­пользуя принцип суперпозиции:

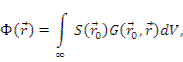
где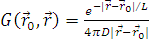

-функция Грина (функция влияния); r ₀ - координата  источника

Длина диффузии

Используя решение для случая точечного источника, можно определить средний квадрат смещения нейтрона от источника до места поглощения:

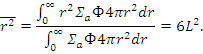
Усреднение r ² выполнено по Σ_аФ - числу поглощений в единицу времени в

единице объема (интенсивности поглощений).

Тогда 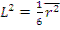 , т.е. квадрат длины диффузии равен 1/6 среднего квадрата

смещения нейтрона от точечного источника до точки его поглощения. При этом общая длина траектории (путь) нейтрона до точки его поглощения всегда боль­ше смещения (расстояния по прямой).

В размножающей среде с равномерным распределением источников быст­рых нейтронов и их замедлением квадрат длины диффузии равен 1 /6 среднего квадрата смещения нейтрона от точки, где он стал тепловым, до точки его поглощения.

Длина диффузии определяется основными характеристиками среды: коэф­фициентом диффузии D и сечением поглощения Σ_а. Используя связь D с Σ_tr, получим следующую формулу для длины диффузии тепловых нейтронов:

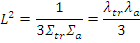
В табл.7.1 приведены значения длин диффузии тепловых нейтронов в различных средах, а также коэф­фициента диффузии и сечения по­глощения [3]. Как видно из табл.7.1, длина диффузии, в первую очередь, определяется поглощающими свой­ствами среды.

Длина диффузии зависит от тем­пературы среды. На величину L температура влияет двояко – через плотность (γ), зависящую от температуры, и непосредственно через температу­ру (температуру нейтронного газа) ( 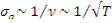). Для неводяных сред L воз­растает с увеличением температуры замедлителя. Для воды зависимость L от температуры имеет иной характер из-за существенной зависимости длины пе­реноса от энергии нейтронов.

Время диффузии t _диф =λ_а /v - это время жизни тепловых нейтронов.

Альбедо

Альбедо - это отражающая способность или коэффициент отражения (поня­тие, заимствованное из оптики).

Альбедо нейтронов 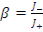       где J ₊ , J_ - плотности односторонних токов

нейтронов на входе и выходе в отражатель соответственно. Для плоской границы:

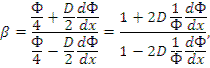
где 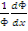 значение на границе.

Значения альбедо определяются диффузионными константами среды и бли­зостью границы отражателя с пустотой. Нейтроны отражаются не от плоско­стей, а от объемов вещества. Если толщина отражателя мала по сравнению с длиной диффузии, то многие нейтроны достигают границы с пустотой и поки­дают объем тела. Поэтому уменьшение толщины отражателя снижает альбедо.

Альбедо отражателя конечной толщины а (плоская граница):

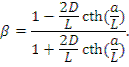
Значения альбедо бесконечной среды велики. В табл.7.1 приведены значе­ния альбедо различных сред. Когда a >2 L , отражатель можно считать бесконеч­ным. В таком случае альбедо зависит только от диффузионных констант среды. Альбедо отражателя бесконечной толщины (плоская граница):

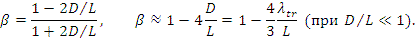
При увеличении L возрастает β. При увеличении 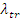 уменьшается β. Длина диффузии L характеризует сохранность нейтронов, транспортная длина  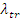-глубину проникновения нейтронов в отражатель (расстояние, на котором тра­ектория нейтронов поворачивается на угол  π/2).

Благодаря высоким коэффициентам отражения, каждый нейтрон в процессе диффузии многократно пересекает некоторую условную плоскость внутри объ­ема тела. Соседние объемы вещества много раз обмениваются одними и теми же порциями нейтронов, что создает высокие концентрации нейтронов в кон­денсированных средах, которые наблюдаются на опыте и в сравнении с кото­рыми концентрации в направленных нейтронных потоках в пустом пространст­ве пренебрежимо малы. По той же причине диффузионный ток 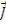 обычно мал в сравнении со скалярным потоком Ф.