Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Рассмотрим замедление нейтронов, испускаемых моноэнергетическим ис­точником, в непоглощающей среде из тяжелых ядер. В таком случае адекватна модель непрерывного замедления.

На рис.8.1 представлена качественная зависимость u = ln ( E_f / E ) от времени t .

зависимость имеет ступенчатый вид. Такая зависимость инди­видуальна для каждого нейтрона. В среднем высота ступенек постоянна и равна среднелогарифмической потере энергии на одно столкновение 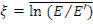. В сре­дах из достаточно тяжелых ядер (неводородсодержащих) нейтрон испытывает много соударений при замедлении до тепловой энергии. Высота ступенек в таких средах мала, поэтому реальную зависимость можно заменить плавной (штриховая линия) - модель непрерывного замедления. Такая модель математически описывается диффузионными уравнениями, записываемыми для непрерывных функций.

Примем, что все нейтроны, диффундировавшие в течение времени t после рождения, имеют скорость ν. Тогда число столкновений одного нейтрона за время 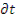 равно 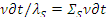 или 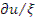. Приравнивая данные выражения, получа­ем соотношение, связывающее летаргию со временем,

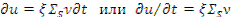                               (8.1)

Данное выражение определяет непрерывную зависимость между летаргией и временем (показана на рис.8.1 пунктиром). Оно подменяет дискретную картину замедления непрерывным замедлением.

Уравнение возраста

 

Предположим, что в момент t =0 испускается некоторая порция нейтронов с энергией E ₀ . Эта порция диффундирует (распределяется по всё возрастающему объему) и замедляется (снижая энергию). В произвольный момент времени t число нейтронов в единице объема вокруг произвольной точки 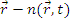. Это распределение подчиняется нестационарному уравнению диффузии. Источников в момент времени t>0 в этой точке нет (источник есть только при энергии E₀ что соответствует времени t =0). В результате, нестационарное уравнение диффузии при отсутствии поглощения будет выглядеть следующим образом:

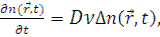                                                        (8.2)

так как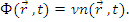

Между плотностью нейтронов в шкалах времени и летаргии можно записать следующее соответствие: 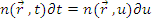, если  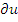соответствует 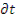. В данном выражении  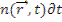- число нейтронов в единице объема вокруг точки  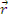за время после выхода из источника oт t до 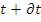, а 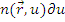 - число нейтронов в единице объема вокруг точки 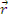, имеющих летаргию от и до  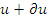Тогда

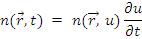
Заменяя 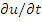 выражением (8.1), получим

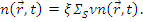                                                        (8.3)                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                           

Записываем тождество

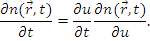
Заменяя 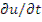 выражением (8.1), получим

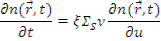
Воспользуемся (8.3) и получим

 

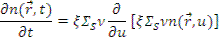
Подставляя выражения (8.3) и (8.4) в уравнение диффузии (8.2), получим

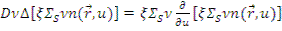                                     (8.4)

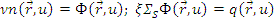 (1/(см³ с)) - плотность замедления.

Тогда

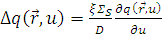 - нестационарное уравнение диффузии замедляющихся нейтронов.

Можно записать данное уравнение в функции энергии

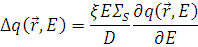
где .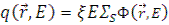

Введем новую переменную τ, определив её следующим образом:

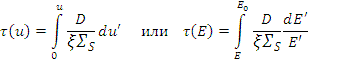
 Тогда 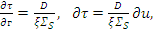и с учетом этого перепишем уравнение

диффузии замедляющихся нейтронов

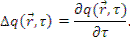
Данное уравнение называется уравнением возраста, в котором τ - возраст

нейтронов с летаргией и, [τ]=см², .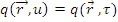

Данное уравнение было получено Ферми. По виду оно совпадает с уравне­нием теплопроводности, в котором в правой части вместо дифференцирования по времени стоит дифференцирование по возрасту. Однако возраст к хроноло­гическому времени замедляющегося нейтрона имеет лишь то отношение, что увеличивается со временем. Его физический смысл идентичен смыслу квадрата длины диффузии теплового нейтрона. Возраст описывает перемещение в пространстве замедляющихся нейтронов и просто связан со средним квадратом перемещения при замедлении .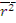

Уравнение возраста - нестационарное уравнение диффузии замедляющихся Нейтронов. Это уравнение в частных производных второго порядка, оно должно быть дополнено начальными и граничными условиями.

Начальные условия

Точечный источник мощностью S расположен в точке 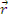 = 0:

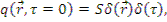
где 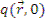 - число нейтронов в единице объема в единицу времени, начинаю­щих замедление; δ - дельта-функция Дирака, т.е. плотность замедления ней­тронов с τ=0 в точке  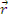= 0 равна мощности источника S в данной точке (  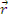= 0 ) - предполагается, что все нейтроны рождаются с одной и той же энер­гией и возраст нейтронов источника равен нулю.

Точечный источник мощностью S расположен в точке :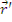

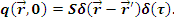
Распределенный источник:

 

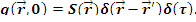
где 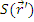 - мощность источника в точке .

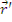Граничные условия

Граничные условия, полученные ранее для диффузии моноэнергетических нейтронов, справедливы и для диффузии замедляющихся нейтронов.

1. Условия на границе, разделяющей две среды: должны быть непрерывны плотность потока и первая производная (градиент) потока, умноженная на коэффициент диффузии в среде:

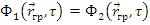
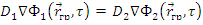
Переходя от плотности потока Ф к плотности замедления q , получим

 

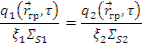
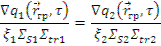
2. Условие на внешней поверхности среды (границе тела с вакуумом)

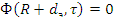
Граничные условия должны выполняться для всего спектра энергий ней­тронов.

Условия применимости уравнения возраста:

1.  Справедливо диффузионное приближение.

2. Тяжелый замедлитель, для которого справедлива модель непрерывного замедления ( 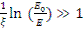, т.е. бесконечно много соударений до того, как летаргия

станет равной и).

Решения уравнения возраста в простейших случаях

Уравнение возраста решается с помощью преобразований Фурье. Решение для точечного источника

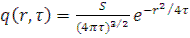                                                  (8.5)

Следовательно, плотность замедления описывается распределением Гаусса.

Если τ мало, т.е. велика энергия, то ней­троны находятся вблизи точечного источ­ника (рис.8.2). С ростом τ по мере замед­ления пространственное распределение всё больше расплывается. Наконец, при достижении тепловой энергии последняя зависимость дает распределение источни­ков тепловых нейтронов 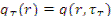 око­ло точечного источника быстрых нейтро­нов.

Обобщенная формула для плоского, линейного, точечного источников:

 

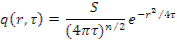
Для плоского источника п=1, тогда S-число нейтронов, испускаемых едини­цей поверхности источника. Для линейного источника n=2, тогда S - число ней­тронов, испускаемых единицей длины. Для сферического (точечного) источни­ка п=3.

В случае непрерывного расположения источников выражение для плотности замедления можно записать, используя принцип суперпозиции источников, в виде

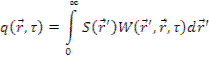
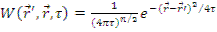— функция влияния для замедляющихся нейтронов (функция Грина). Функция влияния представляет собой вероятность того, что быстрый нейтрон, рожденный в точке 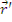, будет иметь возраст τ в точ­ке .

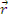Возраст нейтронов

Используя решение для случая точечного источника, можно определить средний квадрат смещения нейтронов от источника при замедлении нейтронов до энергии, соответствующей возрасту τ:

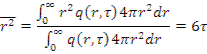
где q - плотность замедления для точечного источника (поглощение отсутству­ет, рассеяние упругое).

Тогда 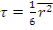, т.е. возраст тепловых нейтронов равен 1/6 среднего квадрата

смещения нейтрона от точечного источника (от точки рождения) до точки, где его энергия в процессе замедления стала тепловой.

При этом 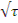 — длина замедления.

В табл.8.1 приведены экспериментальные значения возраста тепловых нейтронов от источника нейтронов деления при нормальных условиях [3].

Утечка замедляющихся нейтронов из объема тела будет небольшой, если выполняется условие 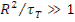 , где R — характерный размер тела. В энергетических реакто­рах достаточно, чтобы .

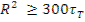Возраст тепловых нейтронов τ_т и квадрат длины диффузии L описывают смещение нейтронов в пространстве соответст­венно при замедлении и диффузии в тепловой области и составляют квадрат длины миграции (площадь миграции):

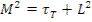
Площадь миграции равна 1/6 среднего квадрата смещения нейтрона от точки  рождения до точки его поглощения. При этом 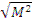   - длина миграции.

Теория возраста дает тем лучшее согласие с опытом, чем тяжелее вещество-замедлитель и соответственно меньше ξ, т.е. чем ближе механизм потерь энергии к модели непрерывного замедления и больше число столкновений при за­медлении. Поэтому в водородсодержащих средах теория возраста непримени­ма. Это связано в первую очередь с большой величиной ξ. Большая часть сме­щения нейтронов в водородсодержащих средах связана с несколькими первыми столкновениями, а теория возраста неприменима к случаю малого числа столк­новений. Поэтому распределение (8.5) не имеет места в таких средах. Однако по аналогии с другими замедлителями величина 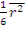    называется возрастом и в водородсодержащих средах.

Время замедления

Из зависимости (8.1) между хронологическим временем замедляющегося нейтрона и его энергии 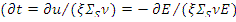 можно найти время замед­ления до тепловой энергии [5]:

 

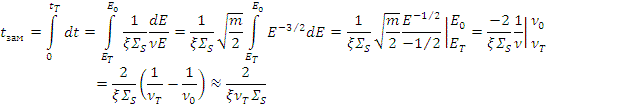
где 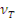=2,2 10³ м/с и 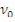=2 10⁷ м/с - скорости теплового нейтрона и нейтрона де­ления соответственно;  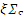усреднено по интервалу замедления.

В табл.8.2 приведены время замедления в замедлителях от E ₀ =2 МэВ до

E_т=0,025 эВ и время диффузии в тепловой

области 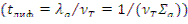 [3]. Время диффузии примерно в 100 раз больше, чем время замедления. В ядерных реакторах на тепловых нейтронах, благодаря наличию урана, поглощающего нейтроны, время диффузии уменьшается. Однако оно составляет ~10^-3 с в реакторах с графитовым  и тяжеловодным замедлителем и  ~10^-4 с в

реакторах с обычной водой, что всё равно много больше времени замедления. В ре­акторах на быстрых нейтронах замедления практически нет и полное время жизни нейтрона очень мало - около 10^-7 с. Хотя сечения поглощения в области энергии быстрых нейтронов невелики, и нейтрон до поглощения испытывает много столкновений с ядрами атомов среды, благодаря скорости порядка 10⁷ м/с это происходит за очень малое время.