Вытеснение растворами активной примеси. Неизотермическая фильтрация. Особенности фильтрации неньютоновских систем.
1 Программа курса “Подземная гидромеханика”
Введение
Подземная гидромеханика - теоретическая основа разработки нефтяных и газовых месторождений. Важнейшие этапы развития подземной гидромеханики.
Основные понятия и определения
Пористость, просветность, объемный и массовый расходы, скорость фильтрации и действительная скорость, модели грунтов. Одномерные фильтрационные потоки: плоскопараллельный, плоскорадиальный и сферический
Дифференциальные уравнения фильтрации
Закон Дарси. Пределы применимости закона Дарси. Нелинейные законы фильтрации. Фильтрация неньютоновских жидкостей. Уравнение неразрывности потока. Зависимость параметров флюидов и пористой среды от давления. Начальные и граничные условия.
Установившееся движение несжимаемой жидкости по закону Дарси
Дифференциальные уравнения установившегося движения. Формулы дебита, распределения давления, скорости фильтрации, времени движения частиц. Индикаторные линии. Фильтрация в слоистых и зонально-неоднородных пластах. Средняя проницаемость пласта. Приток жидкости к несовершенным скважинам. Виды несовершенства. Опыты Щурова. Приведенный радиус скважины.
Установившееся движение упругой жидкости и газа в пористой среде.
Дифференциальные уравнения установившегося движения упругой жидкости по закону Дарси. Аналогия с движением несжимаемой жидкости. Функция Лейбензона. Плоскопараллельный и плоскорадиальный потоки. Исследование газовых скважин на стационарных режимах. Индикаторные линии. Приток газа при нарушении закона Дарси. Определение фильтрационных коэффициентов “a” и “b”.
Интерференция скважин
Точечный источник и сток. Метод суперпозиции решений. Приток жидкости к группе скважин с удаленным контуром питания. Приток к скважине у прямолинейного контура питания. Приток к скважине у непроницаемой границы. Метод отражения. Приток к цепочкам скважин. Метод фильтрационных сопротивлений Борисова.
Неустановившееся движение упругой жидкости в упругой пористой среде.
Особенности проявления упругого режима. Упругий запас. Коэффициент уругоемкостиупругоемкости пласта. Дифференциальное уравнение упругого режима. Аналогия с задачей теплопроводности. Начальные и граничные условия. Приток упругой жидкости к галерее при постоянном перепаде давлений. Приток к скважине. Основная формула упругого режима. Исследование скважин при нестационарных режимах. Принцип суперпозиции при упругом режиме. Приближенные методы решения задач упругого режима. Метод последовательной смены стационарных состояний. Приток жидкости к укрупненной скважине.
Неустановившаяся фильтрация газа в пористой среде.
Дифференциальное уравнение неустановившейся фильтрации газа в пористой среде по закону Дарси. Лианеризация уравнения. Исследование газовых скважин при нестационарных режимах.
Взаимное вытеснение несмешивающихся жидкостей.
Поршневое вытеснение несмешивающихся жидкостей. Кинематические условия на подвижной границе. Уравнение движения границы раздела при плоско - радиальном движении. Основы теории образования конуса при наличии подошвенной воды. Двухфазное вытеснение несмешивающихся жидкостей. Обобщенный закон Дарси. Уравнение неразрывности. Теория Баклея - Леверетта. Определение фронтальной и средней насыщенности. Капиллярное давление.
Гидродинамические методы повышения нефте- и газоотдачи пластов.
Вытеснение растворами активной примеси. Неизотермическая фильтрация. Особенности фильтрации неньютоновских систем.
1 Контрольные задания
УКАЗАНИЯ К ВЫПОЛНЕНИЮ КОНТРОЛЬНЫХ ЗАДАНИЙ
Цель контрольных заданий — способствовать более глубокому изучению основных положений дисциплины и лучшему усвоению приемов использования этих положений для решения инженерных задач.
Прежде чем приступить к выполнению контрольного задания, необходимо хорошо изучить соответствующие разделы курса. Сталкиваясь с той или иной расчетной формулой, студент должен научиться не только применять эту формулу для расчета, но и понять ее сущность и те закономерности, которые она отражает, а также проанализировать размерности входящих в нее величин.
Ответы на контрольные вопросы должны быть краткими, но не в ущерб ясности и полноте изложения. Следует обращать внимание на правильность терминологии и четкость ответов. Ответы на вопросы необходимо писать лишь после того, как проработана вся тема в целом, но отнюдь не в процессе ее изучения, так как законченный и четкий ответ можно дать только после изучения всей темы. Номера вопросов, на которые следует ответить, и номера задач, которые нужно решить, определяются по таблице вариантов в зависимости от сочетания букв в фамилии студента. Номер первой задачи соответствует первой букве фамилии, второй задачи — второй букве и т д. Номера вопросов определяют по пятой букве фамилии студента. Например, студент Петров должен решить задачи 3, 6, 14 и ответить на вопросы 3, 8, 12, 18, 23, 25. Если фамилия студента содержит меньше восьми букв, номера последующих задач и вопросов будут соответствовать последней букве фамилии. Например, студент Чуб должен включить в первую контрольную работу задачи 4, 9, 11 и вопросы 5, 7, 15, 17, 25, 32 (табл. на с. 12).
| Буквы алфавита | Номера задач | Вопросы | |||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ||
| а | 1.1 | 1.13 | 2.1 | 3.1 | 2.13 | ||||
| б, в | 1.2 | 1.14 | 2.2 | 3.2 | 2.14 | ||||
| г, д | 1.3 | 1.15 | 2.3 | 3.3 | 2.15 | ||||
| е, ж, з, и | 1.4 | 1.16 | 2.4 | 3.4 | 2.16 | ||||
| к | 1.5 | 1.17 | 2.5 | 3.5 | |||||
| л | 1.6 | 1.18 | 2.6 | 3.6 | |||||
| м | 1.7 | 1.19 | 2.7 | 3.7 | |||||
| н, о | 1.8 | 1.20 | 2.8 | 3.8 | |||||
| п, р | 1.9 | 1.21 | 2.9 | 3.9 | |||||
| с | 1.10 | 1.22 | 2.10 | 3.10 | |||||
| т, у, ф, х | 1.11 | 1.23 | 2.11 | 3.11 | |||||
| ц, ч, ш, щ, ъ, ы, ь, э, ю, я | 1.12 | 1.24 | 2.12 | 3.12 | |||||
Задача 20
Определить дебит дренажной галереи шириной В =100 м, если толщина пласта h=10 м, расстояние до контура питания L=10 км, коэффициент проницаемости пласта k=1 Д, динамический коэффициент вязкости жидкости m=1 мПа с, давление на контуре питания p1, =9,8 МПа (100 МПа) и давление в галерее рг=7,35 МПа (75 МПа). Движение жидкости напорное, подчиняется закону Дарси.
Ответ: Q=21,6 мз/сут.
Задача 21
Определить коэффициент проницаемости пласта, если известно, что в пласте происходит одномерное, плоскопараллельное установившееся движение однородной жидкости по закону Дарси. Гидравлический уклон l =0,03, ширина галереи B=500 м, толщина пласта h=6 м, плотность жидкости р=850 кг/м3, динамический коэффициент вязкости m =5 мПа с и дебит галереи Q=30 м3/суг
Ответ: k =2,27 Д=2,32. 10-88 cм2=2,32• 10-122 м2.
Задача 22
Показать графически распределение давления и найти градиент давления при плоскопараллельном движении в пласте несжимаемой жидкости по линейному закону фильтрации, используя следующие данные: длина пласта L =5 км, толщина пласта h=10 м, ширина галереи B=300 м, коэффициент проницаемости пласта k =0,8 Д, давление в галерее рг= =2,94 МПа (30 МПа), динамический коэффициент вязкости жидкости μ =4 мПа с, дебит галереи Q=30 м3/сут.
Ответ: р=5,78— 0,0568- 10-22 х (х в м, р в МПа), dp -=0,0568. 10-22 МПа/м
Задача 23
Определить дебит газовой скважины (в т/сут) в случае установившейся плоскорадиальной фильтрации жидкости по закону Дарси, если известно, что давление на контуре питания Л =9,8 МПа (100 МПа), давление на забое скважины Р( = =7,35 МПа (75 МПа), коэффициент проницаемости пласта k=0,5 Д, толщина пласта h=15 м, диаметр скважины D, = =21,8 см, радиус контура питания Rk=10 км, динамический коэффициент вязкости жидкости m =6 мПа-с и плотность жидкости (ro=850 кг/м''.
Ответ: Q,„=127 т/сут
Задача 24
Определить давление на расстоянии 10 и 100 м от оси скважины при плоскорадиальном установившемся движении несжимаемой жидкости по линейному закону фильтрации, считая, что коэффициент проницаемости пласта k=0,5 Д, толщина пласта h=10 м, давление на забое скважины р =7,84 МПа (80 МПа), радиус скважины гc =12,4 см, динамический коэффициент вязкости нефти m=4-10-3 кг/м-с, плотность нефти Ro=870 кг/м3 и массовый дебит скважины Q,„-=200 т/сут.
Ответ: p1=9,28 МПа; ð2= 10,06 МПа.
Задача 25
Построить индикаторную линию (зависимость дебита Q о г перепада давления Dip =pk—рс), имеющуюся при установившейся плоскорадиальной фильтрации жидкости по линейному закону, если известно, что давление на контуре питания pk =8,82 МПа (90 МПа), коэффициент проницаемости пласта k=600 дм, толщина пласта h=10 м, диаметр скважины D,_== =24,8 см, расстояние от оси скважины до контура питания Rk=10 км и динамический коэффициент вязкости нефти ,LI=5 мПа с.
Ответ: индикаторная линия—прямая, описываемая уравнением Q=5,77 Ар (Q в м3/сут, Ар в МПа).
Задача 26
Определить коэффициент гидропроводности пласта kh/mu по данным о коэффициенте продуктивности скважины. Известно, что фильтрация происходит по закону Дарси, коэффициент продуктивности K=18 т/сут (кгс/см2), среднее расстояние между скважинами 2 =1400 м, плотность р=925 кг/м3, радиус скважины rc=0,1 м.
Ответ: kh/m =3,18-10-9 м4 с/кг (318 Д.см/мПа с).
Задача 27
Определить средневзвешенное по объему пластовое давление, если известно, что давление на контуре питания Pk =100 МПа, давление на забое возмущающей скважины Pс=80 МПа, расстояние до контура питания Rk =25 км, радиус скважины rс=10 см. В пласте имеет место установившееся плоскорадиальное движение несжимаемой жидкости по закону Дарси.
Ответ: р=9,72 МПа (99,19 МПа).
Задача 28
Определить относительное понижение Dр./s= (Hk—H)(Hk—Hñ) пьезометрического уровня в реагирующих скважинах, расположенных от возмущающей скважины на расстояниях м, 100 м, 1 км, 10 км. Движение жидкости установившееся плоскорадиальное по закону Дарси. Радиус скважины rñ = 0,1 м, расстояние до контура питания Rk =100 км.
Ответ: Sp/s равно соответственно 0,83; 0,50; 0,33; 0,167.
Задача 29
Определить время отбора нефти из призабойной зоны скважины радиусом rc=100 м, если толщина пласта h=10 м, коэффициент пористости пласта m =20%, массовый дебит нефти Qm =40 т/сут, плотность ее р—920 кг/м33, г, =0.1 м.
Ответ: Т=1440 сут.
Задача 30
Определить время t, за которое частица жидкости подойдет стенке скважины с расстояния Ro=200 м, если коэффициент проницаемости пласта k=1 Д, динамический коэффициент вязкости нефти m = 5 мПа с, депрессия во всем пласте радиусом Rk =1 км составляет pk—pc =10 МПа; толщина пласта h = 10ì, коэффициент пористости пласта m =15%, радиус скважины =10 см. Ответ: t=1600 сут.
Задача 31
Как изменится дебит скважины Q при увеличении радиуса скважины вдвое?
1. Движение происходит по линейному закону фильтрации.
2. Фильтрация происходит по закону Краснопольского. Начальный радиус скважины rc=0,1 м. Расстояние до конура питания Rk=5 км.
Ответ: 1) Q : Q = 1.07; 2) Q' : Q =1,41 т. е. при движении
жидкости по линейному закону фильтрации влияние изменения
радиуса скважины менее интенсивно, чем при движении по
закону Краснопольского.
Задача 32
Найти изменение перепада давления Ар при увеличении радиуса скважины вдвое, при котором дебит остается прежним. 'рассмотреть два случая, как в предыдущей задаче. Начальный радиус скважины rc=0,1 м, расстояние до контура питания Rk= 1 км.
Ответ: 1) Ë/?7Ëð= 0,925, 2) À///À/?=0,5.
Задача 33
Во сколько раз необходимо увеличить радиус скважины, чтобы дебит ее при прочих равных условиях удвоился?
- 1) Движение жидкости происходит по закону Дарси.
5. Контрольные вопросы
Библиографический список
Оглавление
ПОДЗЕМНАЯ ГИДРОМЕХАНИКА 1
5. КОНТРОЛЬНЫЕ ВОПРОСЫ 9
БИБЛИОГРАФИЧЕСКИЙ СПИСОК 9
Задача 9
Определить коэффициент фильтрации, если известно, что площадь поперечного сечения образца песчаника Р = 30 см?, длина образца /=15 см, разность давлений на входе жидкости в образец и на выходе А/? = 0,2ай, плотность жидкости Ro = 1000 кг/м3, и расход равен 5 л/час.
Ответ: с = 3,47-10~3 см/сек.
Задача 10
Определить скорость фильтрации и среднюю скорость движения нефти у стенки гидродинамически совершенной скважины и на расстоянии г = 75 м от скважины, если известно, что толщина пласта h = 10 м, пористость его т = 12 % радиус скважины гс=0,1 м, весовой дебит скважины О = — 50 т/сут, и плотность нефти ? = 850 кг/м3.
Задача 11
Определить скорость фильтрации газа у стенки гидродинамически совершенной скважины, если известно, что приведенный к атмосферному давлению объемный расход газа Qaт = , радиус скважины гс~0,1 м, толщина пласта Л = 20 м, абсолютное давление газа на забое рс ж 50 aт.
Решение:
Из уравнения неразрывности для установившегося потока
Q= ^" Т»т
If
Из уравнения состояния идеального газа при изотермическом процессе следует, что
Нал
поэтому объемный дебит на забое
Скорость фильтрации
задача
Через два однородных образца пористой среды, содержащих глинистые частицы, с целью определения коэффициента проницаемости и коэффициента фильтрации пропускали:
а) пресную воду при £ = 20°С при перепаде давления 500 мм рт. ст. с расходом Q = 2 смя/мин,
в) соленую воду с удельным весом т Ro = кг/ м3 и вязкостью μ = 1,1 мПа с при той же разности давлений, что и в случае а) и с расходом Q = 0,12 см3/сек.
Размеры образцов: длина 1 = 5 см, площадь поперечного сечения } = 5 см?. Найти отношение проницаемостей для случаев айв.
Решение:
В случае одномерной, плоскопараллельной установившейся фильтрации несжимаемой жидкости по закону Дар-си определим k из формулы:
k-9sL
№' Найдем значение
Учитывая, что при t — 20°С для пресной воды ?= 1000^Л£ р
а (Mu = 1 мПа с, получим
a)
Коэффициент фильтрации
в)
В случае эксперимента с пресной водой значения коэффициентов проницаемости и фильтрации оказались меньше, чем в эксперименте с соленой водой, т. к. в первом случае сказывается эффект набухания глинистых цементирующих веществ, что вызывает уменьшение поперечного сечения поровых каналов.
За дача 13
Определить коэффициент пористости, зная, что скорость движения через образец, определяемая при помощи индикатора, равна v = 3 10 см/сек, коэффициент проницаемости. k =0,2 Д, абсолютная вязкость жидкости μ = 4 мПа с и разность давлений Dp = 2 am при длине образца L= 15 см.
Ответ: т = 22%.
3 а 3адача 14
Определить скорость фильтрации у входа жидкости в гидродинамически несовершенную по степени вскрытия скважину, если толщина пласта h = 25 м, относительное вскрытие пласта h = 0,6, радиус скважины гс = 0,1 м, дебит жидкости Q = 250 M3/cyт.
Ответ: w — 0,0308 см/сек.
Задача 15
Определить коэффициенты проницаемости и фильтрации для цилиндрического образца пористой среды диаметром d = 5 см, длиной / = 20 см, если разность давлений на концах образца составляет 300 мрт. ст., расход жидкости Q=l,70 л/час, вязкость жидкости μ = 5 мПа с, плотность ее f> — 0,85 г/см*. Найти также скорость фильтрации.
Ответ: k = 5,9 д,
с = 10~3 см/сек, w — 0,024 см/сек.
Задача 16
Определить скорость фильтрации и среднюю скорость движения при плоско-радиальной фильтрации газа к скважине в точке на расстоянии г = 150 м от центра скважины, если давление в этой точке равно р= 80 аг, толщина пласта h = 12 м, пористость его m = 20%, а приведенный к атмосферному давлению дебит Qam=2-106 мъ/сут.
Ответ: w = 0,2625-1Q-2 см/сек, v — \,3\-\Q~* см/сек.
II. ПРЕДЕЛЫ ПРИМЕНИМОСТИ ЗАКОНА ДАРСИ-НЕЛИНЕЙНЫЕ ЗАКОНЫ ФИЛЬТРАЦИИ.
Задача 18
Определить радиус призабойной зоны гьр, в которой нарушен закон Дарси, при установившейся плоско-радиальной фильтрации идеального газа, если известно, что приведен! ный к атмосферному давлению дебит скважины QaT —2-10| м3/сут, толщина пласта Л== Юм, проницаемость k ~Q,Gdapcu\ пористость пласта тя = 19%, динамический коэффициент вязкости газа в пластовых условиях !i=l,4-10~5 кг/м-с&с^ плотность газа при атмосферном давлении и пластовой температуре рат —- 0,7 кг/м3.
Указание. В решении использовать число Рейнольдса по формуле М. Д. Миллионщикова и за ReKp взять нижнее значение /?е„р = 0,022.
Решение:
По М. Д. Миллионщикову
П, _ И>кр,/й"р
Ае*р ~ Ti '
ОТ ' [1
откуда
Re ^,
1/^р где
Р = Рат Р/Рк- (2)
С другой стороны
__ Q,TP,T (3) р2пгкрА
Подставляя (2) в (1) и приравнивая выражения (1) и (3), получим
Оат Рат _ PeKfml* \).р„
p2«rKph /ГРат Р откуда __ *__
— Оат L/'fe'paT _ ________2-10« V"o7(Ti Д>2- LQ-'2-0.7___ _
К1> ~~ 2 п hReKf га1-5 (t ~ 0,864-1№-2-3,14-Ю-0,022-0,191'5- 1,4-10~5
= 7,9 М.
Задача 19
Определить, происходит ли фильтрация в пласте по закону Дарси, если известно, что дебит газовой скважины Q = 200 м3/сут, толщина пласта h = 5 м, коэффициент пористости m =16%, коэффициент проницаемости k =0,2 д, плотность нефти р = 0,8 г/см3, вязкость ее р = 5 мПа∙с. Скважина гидродинамически совершенна, радиус ее гс = 0,1 м.
Решение: Найдем скорость фильтрации на забое скважины
« = -±- = ————2^————— - 0,0738 см/сек.
2ягсЛ 0,864-105.2-3,14-10- £00
Определим число Рейнольдса по Щелкачеву и сопоставим его с критическим значением.
Re ~ 10и)^Р = Ю-0.0738- V 0.2-1,02-10~8 -0,8 _ Q Q36 ~ «2'3(х ~ 0,0148-0,05 ~" '
Re = 0,036 < /teKp = 1.
Задача 21
Определить дебит дренажной галереи шириной B =100 м если толщина пласта h = 10 м, расстояние до контура питания L =10 км, проницаемость пласта k = l мкм2, динамический коэффициент вязкости жидкости M = 1 мПа с, давление на контуре питания рк = 100 ат и давление в галерее рг = 75 ат. Движение жидкости напорное по закону Дарси.
Ответ: Q = 21,6 м3/сут.
Задача 22μ
Определить величину коэффициента проницаемости пласта (в различных системах единиц), если известно, что в пласте происходит одномерное, плоскопараллельное установившееся движение однородной жидкости по закону Дарси. Гидравлический уклон i = 0,03, ширина галереи В Я = 500 м, толщина пласта h = 6 м, плотность жидкости Ro = 850 кг/м3, абсолютная вязкость ее μ = 5 мПа с и дебит галереи реи Q = 30 мъ/сут. Я Ответ: k = 2,27 мкм2 д - 2,32-10~8 см* = 2,32-10~12 м*.
Задача 23
Показать графически распределение давления в пласте при плоскопараллельном движении несжимаемой жидкости по линейному закону фильтрации, используя следующие данные: длина пласта Lк = 5 км, толщина пласта h = 10 ширина галереи B = 300 м, проницаемость пласта k = 800 мд давление в галерее рг = 30 ат, динамический коэффициент вязкости жидкости M = 4 мПа с, дебит галереи Q = 30 мл/сут.
Ответ: р = 59 - 0,058• 10-3 х, х—.в см. Я
ЗАДАЧА 24
Определить дебит газовой скважины (в т/сут) в случае установившейся плоско-радиальной фильтрации жидкости Я закону Дарси, если, известно, что давление на контуре питанияl
I Задача 25
Определить давление на расстоянии 10 и 100 м от скважины при плоско-радиальном установившемся движении несжимаемой жидкости по линейному закону фильтрации, считая, что проницаемость пласта k = 0,5 мкм2, толщина пласта h = 10 м, давление на забое скважины рс = 80 ат, радиус скважины гс = 12,4 см, коэффициент вязкости нефти M. = 4 сантипуаза, плотность нефти = 0,870 m/м3 и весовой дебит скважины G = 200 т/сут. В Ответ: pl = 94,7 ат. p2 = 102,7 ат.
3адача 26
Построить индикаторную линию (зависимость дебита Q of перепада давления dр = (рk - pс), имеющую место при установившейся плоско-радиальной фильтрации жидкости по линейному закону, если известно, что давление на контуре питания рk = 90 ата, проницаемость пласта k = 600 миллидарси, толщина пласта h = 10 м, диаметр скважины Dc = 9' 3/4", расстояние от оси скважины до контура питания RK=10 км и коэффициента вязкости нефти M = 5 сантипуаз. Ответ: Индикаторная линия — прямая, описываемая уравпением Q — 5,77 dр, где Q надо брать в м3/сут, а dр = в am.
Задача 27
Определить значение коэффициента гидропроводнрсти пласта по данным о коэффициенте продуктивности скважины. Известно, что фильтрация происходит по закону Дарси, коэффициент продуктивности n = 18 т/сут ат , среднее рас стояние между скважинами 2 s = 1400 м, плотность нефти =925 кг/м3, радиус скважины гс = 0,1 м.
kh/M = 317,5 мкм2 см/спз.
Ответ: kh/M = 317,5 .
3адача 28
Определить средневзвешенное по объему пластовое давление, если известно, что Давление на контуре питания Рк = 100 ат; давление на забое возмущающей скважины В Pc = 80 ат, расстояние до контура питания Rк= 25 км, радиус скважины rc ~ 10 см. В пласте имеет место установившееся плоско-радиальное движение несжимаемой жидкости по закону Дарси.
Ответ: /7 = 99,19 ат.
Задача 29
Определить относительное понижение пьезометрического уровня в реагирующих скважинах, расположенных от возмущающей скважины на расстояниях 1 м, 100 м, 1 км> 10 км. Движение жидкости установившееся плоско-радиальное по закону Дарси. Радиус скважины гс = 0,1 м, расстояние до контура питания RK — 100 км.
Ответ: г,м 1 100 10» 104 sp:s 0.83 0,50 0,33 0,167
Задача 30
Определить время отбора нефти из призабойнон зоны радиуса г0= 100 м, если толщина пласта Л = 10 м, пористость пласта 20%, весовой дебит нефти G = 40 т/сут, плотность ее Р = 920 кг/м*.
Ответ:' Т = 1440 суток.
Задача 31
Определить время t, за которое частица жидкости подойдет к стенке скважины с расстояния г0 = 200 м, проницаемость пласта k= 1 мкм2, вязкость нефти [х=5 спз, депрессия во всем пласте радиусом R= 1 км составляет/^—рс = 10 МПа; толщина пласта h = 10 м, пористость пласта m = 15%, радиус скважины гс = 10 см.
Ответ: t = 1600 суток.
Задача 32
Как изменится дебит скважины Q при увеличении радиуса скважины вдвое?
1) Движение происходит по линейному закону фильтрации.
2) Фильтрация происходит по закону Краснопольского. Начальный радиус скважины гс = 0,1 м. Расстояние до контура питания RK = 5 км.
Ответ: 1) Q':Q=1,07, 2) Q':Q=1,41, т. е. при движении жидкости по линейному закону фильтрации влияние изменения радиуса скважины оказывается значительно менее интенсивным, чем при движении по закону Краснопольского.
Задача 33
Найти изменение перепада давления Д/7 при увеличении радиуса скважины вдвое, при котором дебит остается прежним. Рассмотреть два случая, как в предыдущей задаче. Начальный радиус скважины гс = 0,1 м, расстояние до контура питания /?к = 1 км.
Ответ: 1) ^ — 0,925, 2) ^ = 0,5. Ьр А/?
Задача 34
Во сколько раз необходимо увеличить радиус скважины, чтобы дебпт ее при прочих равных условиях удвоился?
1) Движение жидкости происходит по закону Дарси.
2) Жидкость фильтруется по закону Краснопольского. Начальный радиус скважины гс = 0,1 м. Расстояние до контypa питания /?к = 1 км.
Решение:
1) Если г'г = игс, то
откуда
п = 4, /•;, = 4-0,1 ж = 0,4 м.
Задача 35
Скважина радиусом гс = 10 см расположена в центре кругового пласта радиусом RK — 350 м. Проницаемость пласта ^ = 0,8 мкм2, толщина h = 12 м, вязкость нефти M = 5 мПа с. Определить дебит скважины, считая, что залежь по контуру радиуса Rк частично непроницаема (см. рис. 9). Контур питания представляет собой в плане дугу окружности радиусом Rк с центральным углом а = 12,6°. Давление на контуре питания рк=^*2$5'ат, давление на забое скважины PС = §0 МПа. i
Решение:
Задача может быть сведена к плоско-радиальной, если формуле Дюпюи за контур питания Cjr ное давление принять средневзвешенное по длине окружности
У / J*C рк = — рк = — 285 = 95 МПа',
J I j-й— 36° збо ; ч • ^с^——П ' ^~ •а>ебит ;
Д ^С >Ч */" Q = 2*kh(PK-Pc) = \
^v ^Л 6.28-0.8-12-102(95—80) _
*^1^ f * ' 0,1
РИС. 9. = 2220 см*/сек = 192 мэ/сут
Задача 36
Сколько жидкости следует закачивать в пласт в единиц времени через нагнетательную скважину, если необходимо чтобы давление в скважине поддерживалось в процессе зг качки на Д/? = 15 МПа выше давления, установившегося в пл; сте на расстоянии г = 2 км от скважины. Имеет место закон Дарси. Вязкость μ = 1 мПа с, проницаемость пласта £=150 м\ толщина пласта h-~ 10 м, радиус скважины гс = 10 см. Ответ: Q = 123 м3/сут.
Задача 38
Круговой газовой пласт радиусом RK = 15 км, толщиной h = 8 м, эксплуатируется пятью скважинами радиусом гс = 7,5 см, из которых четыре расположены в вершина квадрата со стороной d = 150 м, а пятая — в центре (рис. 1 Контурное давление pк = 110 МПа, скважины работают с однаковым забойным давлением рс = 90 МПа.
Коэффициент проницаемости пласта k = 0,6 д, вязкое нефти (M = 1,1 мПа с.
Определить дебиты скважин и отношение дебитов Q5/Q
Ответ: Q1 = 161 м3/сут, Q5 = 130 м3/су т, Q5/Q1 = 0,812.
3адача 39
Найти значения потенциалов на скважинах, расположенных симметрично на расстоянии 2а — 300 м относительно центра кругового контура питания радиуса Rк = 5 км, если известно, что дебит одной составляет 200 т/сут, а другой 300 т/сут, потенциал на контуре питания Фк = 50 см2/сек, радиус скважины гс = 0,1 м, толщина пласта h = 10 м, плотность нефти = 0,85 т/м3.
Указание: Считать, что контур питания одинаково удален от каждой из интерферирующих скважин.
Ответ: Фс1 = 43,5 см2/сек, ФС2 = 41,76 см2/сек.
3адача 40
Определить, при каком постоянном забойном давлении ра ботала скважина №1 с радиусом rc = 0,1 м в круговом пласте радиуса Rк = 10 км, если при введении скважины №2 с таким же радиусом, расположенной на расстоянии 2 s = 150 м от первой и рабо- тающей с .забойным давлением pС2 = 70 МПа, скважина № 1 была полностью заглушена. Давление на контуре питания рк = 100 МПа (рис. 19). Решение: Считая скважины достаточно удаленными от контуpa питания и применяя метод суперпозиции, запишем выражение для потенциала результирующего течения в произвольной точке М. Рис. 19.
Фк - Фм = q/2 Pi Ln^ + ^-1п ^ .
2ге дг, 2л гг
Помещая точку М на контур первой скважины, получим
ф«-ф- = 1г1п;: + 2т1п2Т'
помещая ее на контур второй скважины, найдем Ф — Ф «— -^In — 4- -^-In^
*к ^с2 — 0 о^о —' 2те 2о 2л Гс
Так как скважина №1 полностью заглушена, то ее дебит q1 = 0 и уравнения приобретают вид
Фк - Фс1
ф _ ф — ^Lln^S. • х к ч с2 — „ 111 —— • 2те Гс
Задача 46
Определить дебиты скважин двух круговых батарей с радиусами R1 = 1000 м, R2 = 600 м, расположенных концентрично в круговом пласте с радиусом контура питания
Q>Q'2 QL
PK*~Lo-:i- | ""F^l
J4 A , J2 rh. _i
if 4
Р„ Ра
Рис 25
/?к = 3500 .w. Скважины радиусом rс= 10 см эксплуатируют при постоянных забойных давлениях pci = 100 МПа, pс2 = 95 МПа давление на контуре питания PК = 125 МПа; толщина пласта h = 10 м, проницаемость пласта k = 0,2 д, вязкость нефти M. = 5 мПа с. Число скважин в батареях N1 = 10, N2 = 6.
Решение:
Используя метод Ю. И. Борисова, составим схему эквивалентных фильтрационных сопротивлений (рис. 25).
Определим внешние и внутренние фильтрационные сопротивления:
Pl = _e_ln*£.-——5_2£_ lg-252L = 4,97- 10-з ?L««- ^ 2яйй /?, 6.£8-0,2 Юз Б 1000 ел' '
Р - t* ing.i - 5'2-3 ig 100° =201 ip-»g!^gg Ра~ 2п*Л Шйг ~ 6,28.0,2- 10Slg 600 ^ Ш ^Г ' ,
Для определения внутренних фильтрационных сопротивлений найдем половины расстояний между скважинами первой и второй батарей
_2n*t _ 6.28-1000 _зи
г~~2^~ 2.10 ~С514Л'
2я Да 6,28-600 Q1. ог = -г—— = ————— = о!4 м, 2mz 2-6
' = »* In gl = 5'2'3 Ig 3'4 =271-10-» аТ'СеК ?> Znkm^h nrc 6,28.0.2-10 Ю3 й 3,14.0,1 ' ел»
•_ t* in °3 = 5'2-3 ig зи = Р2 2nkmzh лгс 6,28.0,2-6.103 S 3,14.0,1
= 4 58-Ю-3 ar'CeK '' см*
Используя законы Ома и Кирхгофа, напишем уравнение для участка цепи между контуром питания и забоем скважины первой батареи
/>K-/>ci=(Q;+Q;)Pi + Q;Pi,
и аналогично, между контуром питания и забоем скважины второй батареи:
рк -/>с2=(Q; + Q2) PI + Q2 (ра + Р;).
В полученную систему уравнений подставим данные 25=(Q; + Q2)-4,97-lO-3 + Qi-2,74.10-3
30 - (Q;-bQ2)-4,97-Ю-3+ Q2.(2,04+ 4,58)-Ю-3 > решая уравнения относительно Q', и Q2, найдем
Q; =2180 сх*1сек— 188 м?/сут, Q2 = 1650 см3/сек = 142,6 м*/сут.
Учитывая, что Q[ H'Q2—суммарные дебиты первой и второй батарей, найдем дебиты одной скважины
(?!-?!=-^--18,8 jt'/cj/r,
ffij 10
Qz==?i-l4M^23,8 м*/сут.
m% о
Зад|ча 47
Определить дебаты скважин, расположенных тремя кольцевыми батареями. Давление на контуре питания рк = 170* забойные давления на всех эксплуатационных скважинах сВ каковы и равны pcl - pcz = />,.» = 120 МПа . Радиусы батарей /?! = 4000 м, Я, = 3500 м, /?, = 3000 м Радиус скважин Ц = 0,1 м, радиус контура области питания /?к —20 км. Расстояние между скважинами в батареях 2ох = 2а2 = 2 о, = 40» толщина пласта Л = 10 м, проницаемость k — 1 дат вязкость нефти р = 3 мПа с, Указание: Задачу решать методом эквивалентных фильтрационных сопротивлении Ю. П Борисова.
Ответ: Ql = 57,9 м*/сут, Q2=:22,2 м*/сут, Qs = 10,4 м*/М
Задача 48 •
Определить забойные давления скважин, расположен* в круговом пласте радиуса /?к = 10 км двумя концентричИ ми кольцевыми батареями с радиусами Кг = 2000 м, /д! = 1200 м. Число скважин в батареях /^ = 30, /лг=16;'дев одной скважины первой батареи Qt = 80 M*fcyint второй! <?а = 70 м*1сут; радиус скважины ге= 10 см, толщина пласта h = 15 м, проницаемость пласта k = 0,8 д, вязкость жид! сти (1 = 8 мПа с, давление на контуре питания пласта р — 150 Ш
Ответ: pcl - 121,5 МПа, рл = 119,1 МПа
Задача 49
В полосообразной залежи имеется один ряд эксплуатационных и один ряд нагнетательных скважин, расположенными между контуром питания и эксплуатационными скважина (Рис. 26) Определить необходимое количество нагнетаем; жидкости (SQB), давление нетания рл и утечку жидкости за контур питания (ЕС! цп J* ^или количество поступающ жидкости от контура питания чтобы суммарный дебит эксплуатационных скважин cocifl
К ^ ^ лял IQ, = ЮЭЭ м3/сут. ШирД
Ф
ф ^ залежи равна В = 5000 м, моя к' носи, пласта Л «* 10 л, paccf» . , fa / ние от контура питания до рян ф Т / нагнетательных скважин Lm tr />/// // / / // f — 1500 л, расстояние между рядами скважин £а = 600 расстояние между нагнетательными скважинами 2э„ = 300 Ц. b-BV эксплуатационными скважинами 2о,=400л; все скважины гидродинамически несовершенны, приведенный радиус -ссоставляет r'e = Q,l см, давление на контуре питания рк = 120 L* давление на забое эксплуатационных скважин Pс = 80 МПа. Проницаемость пласта 4 = 0,5*, вязкость нефти μ -4 ел.
Составим схему фильтрационных сопротивлений, отвечающую нашей задаче (рис. 27) и найдем фильтрационные сопротивления, ведя расчет для суммарных дебитов рядов
Внешние сопротивления равны: между контуром питания и нагнетательным рядом
.... У*-1 _ 4-1.5 Ю» _ ^ ^ 1Q_3 а-г-сек . Рн kBh 0,5-5.1№ 103 ' см* '
между рядами скважин
р = -fits. = - 4'6 10*—— «0,96-Ю-3 £1«*.
1 АЙЛ 0,5-5-105.10=> сжз
Для определения внутренних сопротивлений найдем число* эксплуатационных (ma) и нагнетательных (т„) скважин:
--^-^»13В __5000 _17
'«•"ЗГ.—зт~~17'
Дебит, определенный по формуле маске га, оказыва| на 34% больше, чем дебит, определенный без учета при к скважине из нижней части пласта толщинаю h - b 1
3адача 58 1
Используя решения Маскета и графики В. И. Щурова определить величину коэффициента С1 учитывающего несовершенство скважины по степени вскрытия. Известно, скважины диаметром dc = 8" вскрывает пласт мощное h = 25 м на глубину b — 5 ч. Расстояние до контура т питания Rk = 1000 м. 1
Ответ: По Маскету C1 = 15,1. По Щурову C1 = 15,0. I
Задача 59
Используя график В. И Щурова, определить вели коэффициентов Ct и С2, определяющих дополнительные фильтрационные сопротивления, обусловленные несовершенством скважины, соответственно, по степени и по характеру вскрытия, а также приведенный радиус скважины г'с, считать, что нефть притекает к скважине диаметром dс = 24,7 несовершенной как но степени, так и по характеру вскрытия. Толщина пласта h = 12 м, вскрытие пласта b = 7 м, число прострелов на один погонный метр вскрытой мощности та n = 17 отв./м, глубина проникновения пуль в породу = 6,25 см, диаметр отверстия do = 1,1 см.
Ответ: С1 = 2,3, С2 = 2 3, гс = 0,123 см.
3адача 60
Определить коэффициент совершенства скважины, неcовершенной по характеру вскрытия. Забои скважины обсажен и перфорирован при помощи кумулятивного перфоратора, круглых отверстий на 1 пог. м п =10, диаметр отвер d0 = 16 мм, длина канала L' = 100 мм. Радиус скважины = 10 см, расстояние до контура питания Rк = 500 м.
Ответ: 8 = 0,825.
Задача 61
Определить коэффициент C1, учитывающий дополните фильтрационное сопротивление, приведенный радиус коэффициент совершенства 3 гидродинамически несовершенной по степени вскрытия скважины радиуса rс = 0,1 м, находящейся в пласте с круговым контуром питания. Толщина Пласта h =16 м, толщина вскрытой части пласта b = 9,6 м, радиус контура питания Rк = 1 км.
Ответ: С1 = 2,4; г'е = 0,907 см, 8 = 0,793.
Задача 62
Какому коэффициенту С, определяющему дополнительное фильтрационное сопротивление, обусловленное гидродинамическим несовершенством скважины, соответствует d = 0,75? радиус скважины гс = 0,1 м, радиус контура питания Rк = 1 км. Определить также приведенный радиус скважины.
Ответ: С = 3,067, r'c; = 0,466 см.
Задача 63
Скважину исследовали по методу установившихся отборов, изменяя диаметр штуцера и замеряя забойное давление глубинным регистрирующим манометром. Результаты замеров приведены в таблице:
см3 мз dр МПа-сек dp, МПа Q, ——— Q, ——— — —, ———— сек сут Q см310 157 13,5 0,0638 20 256 22,1 0,0782 30 334 28,8 0,0900 40 401 34,6 0,100 50 459 39,7 0,109
определить коэффициент проницаемости, если толщина пласта h = 12 м, вскрытие пласта b = 7 м, диаметр скважины dc = 24,7 см, число прострелов на 1 пог. метр вскрытой мощности пласта n = 8, глубина проникновения пуль в породу L' = 0, диаметр пулевого канала d = 1,l см, половина расстояния до соседних скважин о = Rк = 300 м, вязкость жидкости M = 4 мПа с.
Решение:
Из данных исследования видно, что зависимость между Q и dр нелинейная, т. е. индикаторная линия не будет прямой (рис. 41). Используя двучленную формулу dр = AQ + BQ2 и данные таблицы, построим график зависимости dp/Q от Q (рис. 42). Из графика по точке пересечения прямой dр/Q = A + B Q с осью dp/Q (осью ординат) найдем значение A = 0,04 , а по тангенсу угла наклона прямой к оси абсцисс (Q)-В = 0,00015 . см6
задача 102
Нефтяная залежь площадью S =. 500 га и толщину h = 30 м имеееётимеет пористость m = 20% и водонасыщенность ов = 30%. Сколько нефти можно отобрать за счетсчёт объ упругого расширения жидкостей при падении давления 300 МПа до 200 МПа, если коэффициент сжимаемости втн = 1,5 10-4 1/ат, а коэффициент сжимаемости воды = 3 10-5 1/ат. Пласт считать недеформируемым.
Решение
Считая нефть и воду упругими жидкостями, опре изменение объемобъёмов, занимаемых нефтью и водой про нии давления на dp = 100 МПа dVн = S h m (1-ов) рн dp, dVB = S h m оврв dp, объемобъём вытесненной нефти dVн равен сумме объемобъёмов d Vн = S h m ((1 - ав) рн + аву oВ) dр = 500 10 * 30 0,2 [(1 — 0,3) 1,5 10-4 + 0,3 3 10-5]-1(Я
= 3,42 10 м3.
Задача 103
Определить упругий запас нефти в замкнутой нефтеносности площадью 4500 га, толщиной h = 15 м средневзвешенное пластовое давление изменилось пористость пласта т = 18%, коэффициент сжимаемости втн = 2 10-4 , насыщенность пласта связанной водой коэффициент сжимаемости воды рв = 4,5 10-5 , циент сжимаемости породы 3C= 10-5 .
Ответ: dV3 = 1,35 10 6 мъ.
Задача 104
Определить коэффициент нефтеотдачи за счет упругого расширения нефти, воды и горной породы, если площадь области нефтеносности SH = 1000 га, законтурная вода занимает площадь SB = 10000 га, средняя толщина пласта h = 10 м пористость пласта т = 25%; водонасыщенность в зоне нефтенасыщенность зв=20%, коэффициенты сжимаемости нефти, воды! I породы, соответственно, равны зн = 6 10-5 1/ат, зв = 4,2 10-5 1/ат, зс = 2 10-5 1/ат. Пластовое давление снижается от 180 МПа до 80 МПа.
Решение
Коэффициент нефтеотдачи за счет упругого расширения определяется как отношение объемобъёма нефти, полученного за счет сжимаемости к первоначальному объемобъёму нефти
dV/
n =
Начальный объемобъём нефти
V = S, h m (1 - ав) = 1000 104 10 0,25 (1 — 0,2) = 2 107 м3.
ОбъемОбъём нефти, вытесняемой из зоны нефтеносности при падении давления на dр = 100 МПа за счет сжимаемости нефти пористой среды, равен
dv' = sh h m (1 - oob) з*н dp,
где
зН* = m зя + зс = 0,25 6 10-5 + 2 10-5 =
= 3,5 10-5 см2/кГ, dV' ' = 2 107 3,5 10-5 100 = 7 10^4 м3.
За счет расширения воды и породы в зоне нефтеносности объемобъём вытесненной нефти составит
dV" = Sн h m ов зв* dp,
Литература
1. . Подземная гидравлика: Учебник для вузов/К. С. Басниев, А. М. Власов, И. Н. Кочина, В. М. Максимов. - М.: Недра, 1986, 303 с.
2. Евдокимова В. А., Кочина И. Н. Сборник задач по подземной гидравлике. М., Недра, 1979.
3. Пыхачев Г. Б., Исаев Р. Г. Подземная гидравлика. М. Недра, 1973.
Приложения
Интеграл вероятности
| x | erf(x) | x | erf(x) | x | erf(x) | x | erf(x) |
| 0,000 | 0,0000 | 0,400 | 0,4283 | 1,250 | 0,9229 | 2,250 | 0,9985 |
| 0,020 | 0,0225 | 0,420 | 0,4474 | 1,300 | 0,9340 | 2,300 | 0,9988 |
| 0,040 | 0,0451 | 0,440 | 0,4662 | 1,350 | 0,9437 | 2,350 | 0,9991 |
| 0,060 | 0,0676 | 0,460 | 0,4846 | 1,400 | 0,9522 | 2,400 | 0,9993 |
| 0,080 | 0,0900 | 0,480 | 0,5027 | 1,450 | 0,9597 | 2,450 | 0,9994 |
| 0,100 | 0,1124 | 0,500 | 0,5205 | 1,500 | 0,9661 | 2,500 | 0,9995 |
| 0,120 | 0,1347 | 0,550 | 0,5633 | 1,550 | 0,9716 | 2,550 | 0,9996 |
| 0,140 | 0,1569 | 0,600 | 0,6038 | 1,600 | 0,9763 | 2,600 | 0,9997 |
| 0,160 | 0,1790 | 0,650 | 0,6420 | 1,650 | 0,9803 | 2,650 | 0,9998 |
| 0,180 | 0,2009 | 0,700 | 0,6778 | 1,700 | 0,9837 | 2,700 | 0,9998 |
| 0,200 | 0,2227 | 0,750 | 0,7111 | 1,750 | 0,9866 | 2,750 | 0,9999 |
| 0,220 | 0,2443 | 0,800 | 0,7421 | 1,800 | 0,9890 | 2,800 | 0,9999 |
| 0,240 | 0,2657 | 0,850 | 0,7706 | 1,850 | 0,9911 | 2,850 | 0,9999 |
| 0,260 | 0,2869 | 0,900 | 0,7969 | 1,900 | 0,9927 | 2,900 | 0,9999 |
| 0,280 | 0,3078 | 0,950 | 0,8208 | 1,950 | 0,9941 | 2,950 | 0,9999 |
| 0,300 | 0,3286 | 1,000 | 0,8427 | 2,000 | 0,9953 | 3,000 | 0,9999 |
| 0,320 | 0,3491 | 1,050 | 0,8624 | 2,050 | 0,9962 | ∞ | 1,0000 |
| 0,340 | 0,3693 | 1,100 | 0,8802 | 2,100 | 0,9970 | ||
| 0,360 | 0,3893 | 1,150 | 0,8961 | 2,150 | 0,9976 | ||
| 0,380 | 0,4090 | 1,200 | 0,9103 | 2,200 | 0,9981 |
Интеграл вероятности с точность e < 2,5 10-5 можно рассчитать по формулам:
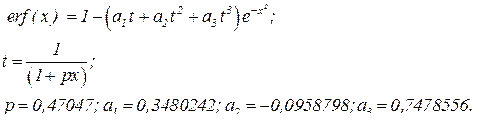 . .
| (7.117) |
В EXCELе в инжинерных функциях есть функция ФОШ(a,b). Интеграл вероятности связан с этой функцией соотношением erf(x) = ФОШ(0,x).
7.2 Интегральная показательная функция E1(x) = -Ei(-x)
| x | E1(x) | x | E1(x) | x | E1(x) | x | E1(x) |
| 0,010 | 4,037 | 0,078 | 2,050 | 0,560 | 0,493 | 3,40 | 0,00789 |
| 0,012 | 3,857 | 0,080 | 2,026 | 0,580 | 0,473 | 3,60 | 0,00616 |
| 0,014 | 3,705 | 0,082 | 2,004 | 0,600 | 0,454 | 3,80 | 0,00482 |
| 0,016 | 3,573 | 0,084 | 1,982 | 0,620 | 0,436 | 4,00 | 0,00377 |
| 0,018 | 3,458 | 0,086 | 1,960 | 0,640 | 0,419 | 4,20 | 0,00296 |
| 0,020 | 3,354 | 0,088 | 1,939 | 0,660 | 0,403 | 4,40 | 0,00233 |
| 0,022 | 3,261 | 0,090 | 1,918 | 0,680 | 0,388 | 4,60 | 0,00184 |
| 0,024 | 3,176 | 0,092 | 1,898 | 0,700 | 0,373 | 4,80 | 0,00145 |
| 0,026 | 3,098 | 0,094 | 1,879 | 0,720 | 0,359 | 5,00 | 0,00114 |
| 0,028 | 3,026 | 0,096 | 1,859 | 0,740 | 0,346 | 5,20 | 0,00090 |
| 0,030 | 2,959 | 0,098 | 1,841 | 0,760 | 0,334 | 5,40 | 0,00071 |
| 0,032 | 2,896 | 0,100 | 1,822 | 0,780 | 0,322 | 5,60 | 0,00057 |
| 0,034 | 2,837 | 0,120 | 1,659 | 0,80 | 0,310 | 5,80 | 0,00045 |
| 0,036 | 2,782 | 0,140 | 1,524 | 0,82 | 0,299 | 6,00 | 0,00036 |
| 0,038 | 2,730 | 0,160 | 1,409 | 0,84 | 0,289 | 6,20 | 0,00028 |
| 0,040 | 2,681 | 0,180 | 1,309 | 0,86 | 0,279 | 6,40 | 0,00022 |
| 0,042 | 2,634 | 0,200 | 1,222 | 0,88 | 0,269 | 6,60 | 0,00018 |
| 0,044 | 2,589 | 0,220 | 1,145 | 0,90 | 0,260 | 6,80 | 0,00014 |
| 0,046 | 2,547 | 0,240 | 1,076 | 0,92 | 0,251 | 7,0 | 1,15 10-4 |
| 0,048 | 2,506 | 0,260 | 1,013 | 0,94 | 0,242 | 7,2 | 9,21 10-5 |
| 0,050 | 2,467 | 0,280 | 0,957 | 0,96 | 0,234 | 7,4 | 7,36 10-5 |
| 0,052 | 2,430 | 0,300 | 0,905 | 0,98 | 0,226 | 7,6 | 5,88 10-5 |
| 0,054 | 2,394 | 0,320 | 0,858 | 1,00 | 0,219 | 7,8 | 4,70 10-5 |
| 0,056 | 2,360 | 0,340 | 0,814 | 1,20 | 0,158 | 8,0 | 3,76 10-5 |
| 0,058 | 2,327 | 0,360 | 0,774 | 1,40 | 0,116 | 8,2 | 3,01 10-5 |
| 0,060 | 2,295 | 0,380 | 0,737 | 1,60 | 0,0863 | 8,4 | 2,41 10-5 |
| 0,062 | 2,264 | 0,400 | 0,702 | 1,80 | 0,0647 | 8,6 | 1,93 10-5 |
| 0,064 | 2,234 | 0,420 | 0,669 | 2,00 | 0,0489 | 8,8 | 1,55 10-5 |
| 0,066 | 2,205 | 0,440 | 0,639 | 2,20 | 0,0371 | 9,0 | 1,24 10-5 |
| 0,068 | 2,177 | 0,460 | 0,611 | 2,40 | 0,0284 | 9,2 | 9,99 10-6 |
| 0,070 | 2,150 | 0,480 | 0,584 | 2,60 | 0,0218 | 9,4 | 8,02 10-6 |
| 0,072 | 2,124 | 0,500 | 0,559 | 2,80 | 0,0168 | 9,6 | 6,44 10-6 |
| 0,074 | 2,099 | 0,520 | 0,536 | 3,00 | 0,0130 | 9,8 | 5,17 10-6 |
| 0,076 | 2,074 | 0,540 | 0,514 | 3,20 | 0,0101 |
При значениях x < 0,01 справедлива формул E1(x) ≈ ln(1/x)-0,5772.
Интегральная показательная функция мажет быть апроксимирована многочленами:
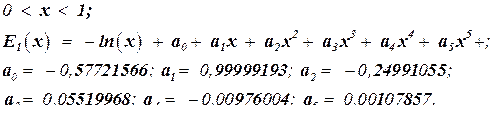 . .
| (7.227) |
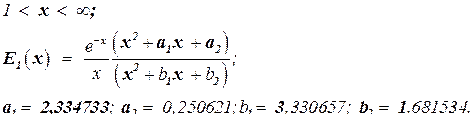 . .
| (7.337) |
ОГЛАВЛЕНИЕ
1. Неустановившееся движение упругой жидкости в упругой пористой среде 1
1.1. Особенности проявления упругого режима 1
1.2. Упругий запас 2
1.3. Дифференциальное уравнение упругого режима 3
1.4. Точные решения некоторых задач упругого режима 5
4.1.1. Приток упругой жидкости к галерее при постоянном перепаде давлений 5
4.1.2. Приток упругой жидкости к галерее при постоянном расходе 10
4.1.3. Приток упругой жидкости к скважине при постоянном расходе. Основная формула теории упругого режима 10
1.5. Интерференция скважин и в условиях упругого режима 15
1.6. Расчет распределения давления при переменном во времени расходе или давлении на забое 18
1.7. Исследование скважин на нестационарных режимах 19
1.8. Приближенные методы решения задач упругого режима 22
8.1.1. Метод последовательной смены стационарных состояний 22
8.1.2. Приток упругой жидкости к с постоянным расходом 23
8.1.3. Приток упругой жидкости к галерее с постоянным давлением 25
8.1.4. Приток упругой жидкости к скважине с постоянным расходом 27
1.9. Примеры и задачи 29
2. Неустановившаяся фильтрация газа в пористой среде 31
2.1. Дифференциальное уравнение неустановившейся фильтрации газа в пористой 31
2.2. нестационарный Приток газа к скважине работающей с постоянным расходом 32
2.3. Исследование газовых скважин на нестационарных режимах 33
2.4. Примеры и задачи 35
3. Взаимное вытеснение несмешивающихся жидкостей. 36
3.1. Обобщенный закон Дарси 36
3.2. Капиллярное давление 41
3.3. Уравнение неразрывности несмешивающих жидкостей 42
3.4. Теория Баклея - Леверетта 45
3.5. Примеры и задачи 51
4. Гидродинамические методы повышения нефте- и газоотдачи пластов 53
5. Программа курса “Подземная гидромеханика” 54
6. Контрольные задания 56
7. Приложения 73
7.1. Интеграл вероятности 73
7.2. Интегральная показательная функция E1(x) = -Ei(-x) 74
Учебное издание
Пятибрат Владимир Павлович
Подземная гидромеханика
Учебное пособие.
Редактор И.А. Безродных
Лицензии ЛР № 020827 от 29.09.1998
План 200 г., позиция 7. Подписано в печать 12.11.2002 г.
Компьютерный набор. Гарнитура Times New Roman.
Формат 60х84 1/16. Бумага офсетная. Печать офсетная.
Усл. печ. л. 2.7, Уч.-изд. л. 2.4. Тираж 150 экз. Заказ №
© Ухтинский государственный технический университет.
169300, г. Ухта, ул. Первомайская 13.
Отдел оперативной полиграфии УГТУ.
169300, г. Ухта, ул. Октябрьская 13
Дата: 2019-03-05, просмотров: 720.