Пусть в неограниченном горизонтальном пласте постоянной толщины h имеетсяимеется добывающая газовая скважина нулевого радиуса (точечный сток). Начальное пластовое давление во всем пластево всём пласте одинаково и равно p_k. В момент времени t = 0 скважина пущена в эксплуатацию с постоянным объемобъёмным дебитом Q_ат0. В пласте образуется неустановившийся плоскорадиальный поток упругого газа. Необходимо рассчитать распределение давления в пласте (в любой его точке в любой момент времени) р ( r, t).

Эта задача анологичнааналогична задачи притока к нефтяной скважине, решегиерешение которой имеееёт вид:

Преобразуем последнее к виду

.,

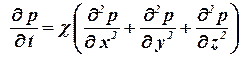(3.9)

Если решать лианеризираванныелинеаризованные дифференциальные уравнения фильтрации газа, то можно воспользоваться аналогией между фильтрацией жидкости и газа. Для этого заменим в этом решении объемобъёмный расход Q на массовый расход Q_m = ρ_ат Q_атo, а давление p на функцию Лейбензона P:

где 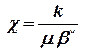- коэффициент пьезопроводности пласта, м²/с.

В случае притока к галереи уравнение упругого режима запишется:

.,

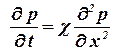(3.10)

Выражая функцию Лейбензона через давление, а массовый расход через объемобъёмный, получим:

а случае притока к скважине:

,

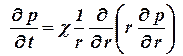(3.11)

или

.

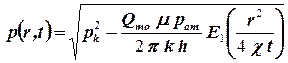(3.12)

Аналогичные преобразования для формулы расчетарасчёта дебита дают

.

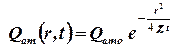(3.13)

Уравнение (1.14) является основным дифференциальным уравнением упругого режима фильтрации. По предложению В. Н. Щелкачева оно названо уравнением пьезопроводности и относится к уравнениям типа уравнения теплопроводности (уравнения Фурье), которое является одним из основных уравнений математической физики.

Коэффициент χ, характеризующий скорость перераспределения пластового давления при неустановившейся фильтрации упругой жидкости в упругой пористой среде, В. Н. Щелкачев назвал коэффициентом пьезопроводности пласта по аналогии с коэффициентом температуропроводности в уравнении теплопроводности.

Размерность коэффициента пьезопроводности χ – м²/с.

Наиболее часто встречающиеся в нефтепромысловой практике значения коэффициента пьезопроводности заключены в пределах от 0,1 до 5 м²/с.

Для того чтобы исследовать неустановившиеся процессы фильтрации упругой жидкости в упругом пласте, надо получить закон распределения давления в пласте р(х, у, z, t). Для этого нужно проинтегрировать уравнение (1.15) при соответствующих начальных и граничных условиях (см. гл. 1).

Рассмотрим наиболее простые точные решения уравнения пьезопроводности приводится ниже.