Углеводородные системы могут быть гомо – и гетерогенными. В гомогенной системе все еееё части имеют одинаковые физические и химические свойства. Составляющие гомогенной системы (называемые компонентами) «размазаны» по всему пространству и взаимодействуют на молекулярном уровне. Для гетерогенной системы физические и химические свойства в разных точках различны. Гетерогенные системы состоят из фаз. Фаза — это часть системы, которая является гомогенной и отделена от других фаз отчетливымиотчётливыми границами. Смесь воды, нефти и газа в пласте — типичный пример гетерогенной среды.

Главными характеристиками движения многофазной системы являются насыщенность и скорость фильтрации каждой фазы.

Насыщенностьюσ _i - порового пространства i - й фазой называется отношение объемобъёма данной фазы V_i к объемобъёму пор V_пор, занятая этой фазой в элементарном объемобъёме:

.

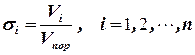(4.1)

Очевидно, что сумма насыщенностей всех фаз равна единице:

.

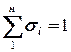(4.2)

Таким образом, в n - фазной системе имеетсяимеется (n - 1) независимая насыщенность. В частности, при исследовании фильтрации смеси двух фаз используется лишь одна из насыщенностей, которая обозначается в дальнейшем sа (обычно это насыщенность вытесняющей фазы). В пористой среде наиболеенаиболее часто происходит фильтрация воды, нефти и газа, поэтому будем обозначать насыщенности этих фаз σ_в, σ_н и σ_г.

Закон Дарси для течения в пористой среде однородной жидкости можно распространить на случай совместного течения двух и болееболее несмешивающихся жидкостей, обобщив понятие проницаемости.

Прежде всего введемвведём понятие скорости фильтрации данной фазы. Скоростью фильтрации данной фазы называется отношение расхода данной фазы к площади поперечного сечения

.

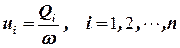(4.3)

Площадка ω пересекает твердуютвёрдую и обе подвижные фазы.

Экспериментально установлено, что расход каждой фазы растетрастёт с увеличением перепада давления и насыщенности данной фазой, а закон фильтрации каждой из фаз по аналогии с законом Дарси можно записать в виде

.

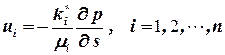(4.4)

где u_i - скорости фильтрации i – той фазы; μ _i – динамический коэффициент вязкости; k _i^* – фазовые проницаемости. Величины k _i^* (i = 1, 2) являются для i ‑ той жидкости проницаемостями в обычном смысле в условиях совместной фильтрации. Эти величины зависят от природы пористой среды (и, прежде всего, от еееё абсолютной проницаемости k, определяемой по данным о фильтрации однородной жидкости), а также от насыщенности пористой среды каждой фазой. При описании многофазных течений обычно вместо фазовых проницаемостей k_i^* вводят так называемые «относительные фазовые проницаемости» k_i определяемые из отношений

.

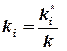(4.5)

В большинстве опытов показано, что для данной структуры пористой среды относительные проницаемости k_i являются в основном функциями насыщенности, а если и наблюдается влияние иных параметров (например, отношения коэффициентов вязкости фаз), то им обычно пренебрегают. Для примера запишем обобщенныйобобщённый закон Дарси при фильтрации трехфазнойтрёхфазной системы вода – нефть – газ вдоль направления s.

.

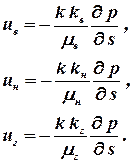(4.6)

Для двухфазной системы вода – нефть приближенные эмпирические формулы для относительных фазовых проницаемостей имеют вид:

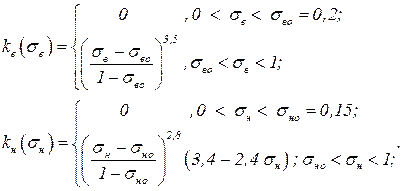
(4.7)

Здесь обозначено σ_{в о}, σ_{н о} – остататочныеостаточные водо и нефте насыщенности.

Для двухфазной системы вода – газ приближенные эмпирические формулы для относительных фазовых проницаемостей имеют вид:

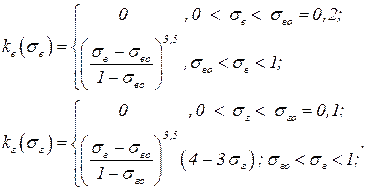
(4.8)

Здесь обозначено σ_{в о}, σ_{н о}, σ_го – остататочные водо, нефте и газо насыщенности.

Типичный вид экспериментальных кривых фазовых проницаемостей k_в(s_в), k_н(s_н), k_г(s_г) приведенприведён на рис.Рисунок - 3.1. Отметим некоторые характерные особенности этих кривых. Для каждой фазы существует предельные насыщенность s_во, s_но, s_го, которые называются остаточными насыщенностями. Движение каждой фазы может происходить только в том случае, если насыщенность этой фазы больше остаточной насыщенности для этой фазы. Таким образом, совместное течение двух фаз (например вода – нефть) имеетимеет место лишь в следующем интервале изменения водонасыщенности для воды σ_во, < σ_в < 1 - σ_но.

Нефтенасыщенность связана с водонасыщенностью σ_н, = 1 - σ_в, поэтому совместное течение происходит при нефтенасыщенностях σ_но, < σ_н < 1 - σ_во.

При движении двухфазной системы (вода – нефть или вода – газ) удобно относительные фазовые проницаемости представлять на одном графике в зависимости фазовых проницаемостей от водонасыщенности рис.Рисунок - 3.3.

Сумма относительных проницаемостей для каждого фиксированного значения а меньше 1.

Рисунок - 4.1. Рис. 3.1. Графики относительных фазовых проницаемостей для воды, нефти и газа

Капиллярное давление

Характерные особенности многофазной фильтрации связаны также с влиянием поверхностного натяжения. Давления в водяной p_в, нефтяной p_н и газовой p_г фазах, вообще говоря, не равны друг другу из–за капиллярных эффектовза капиллярные эффекты, приводящих к скачку давления на границе раздела фаз. Рассмотрим две фазы газ - вода, которые находятся в закрытом с одной стороны капилляре. Считаем, что вода смачивает породу больше, чем газ. Тогда на границе фаз образуется мениск (см. рис 3.3) и давление в газовой фазе больше, чем в водяной. В газовой фазе давление p_г больше, чем в водяной p_в.

Рисунок - 4.2. Рис. 3.2. Схема разности давлений на границе фаз

Разность давлений в фазах на границе раздела называется капиллярным давлением p_k. Капиллярное давление находится по формуле:

В данном случае капиллярное давление зависит от водо и газо насыщенностей. Так, как эти насыщенности удовлетворяют уравнению (3.2), поэтому можно считать, что оно зависит или от водонасыщенности или от газонасыщенностиот газонасыщенности. В случае гидростатики (когда скорость фильтрации равна нулю) капиллярное давление можно найти по формуле Лапласа

.

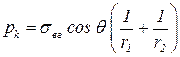(4.10)

где s_вг — коэффициент поверхностного натяжения на границе раздела вода – газ;

q - угол смачивания на этой границе;

r₁, r₂ -  радиусы кривизны границы раздела фаз.

Капилляры имеют разные размеры, при движении фаз он деформируются, водонасыщенность в разных капиллярах разная, поэтому радиусы кривизны границы раздела фаз меняются. Радиус капилляра в модели идеального грунта равен:

.

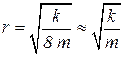(4.11)

Поэтому зависимость капиллярного давления можно представить формулой, которая подтверждается экспериментально:

.

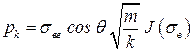(4.12)

где J(s_в) – безразмерная функция Леверетта.

БольшееБольше давление будет на стороне жидкости, не смачивающей твердыетвёрдые зерна породы.

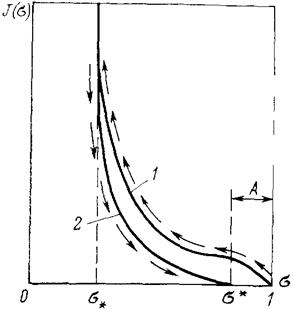1 - кривая вытеснения 2 - кривая пропитки. Рисунок - 4.3.Рис. 3.3. Зависимость капиллярного давления от водонасыщенности

Будем предполагать, как это принято, что капиллярное давление при совместном течении жидкостей совпадает с капиллярным давлением в равновесном состоянии для того же значения насыщенности и при одном и том же направлении еееё изменения (увеличении или уменьшении).

Процессы многофазной фильтрации идут по разномупо-разному в зависимости от характерного времени фильтрационного процесса и от размеров области течения. Капиллярные силы создают в пористой среде перепад давления, величина которого ограничена и не зависит от размеров области фильтрации. Вместе с тем перепад внешнего давления, создающего фильтрационный поток между двумя точками, пропорционален скорости фильтрации и расстоянию между этими точками. Если размеры области малы, то при достаточно малых скоростях фильтрации капиллярные силы могут превзойти внешний перепад давления. Напротив, если рассматривается движение в очень большой области (например, в целой нефтяной или газовой залежи), то влияние капиллярных сил на распределение давления незначительно и их действие проявляется в локальных процессах перераспределения фаз. Взаимное торможение фаз, благодаря которому относительные фазовые проницаемости не равны соответствующим насыщенностям, обусловлено, прежде всего, капиллярными эффектами. В тех случаях, когда можно пренебречь капиллярным скачком p_k(s), капиллярность косвенно учитывается самим видом опытных кривых относительных проницаемостей.

Таким образом, при описании многофазной фильтрации увеличивается число параметров, подлежащих определению. Наряду с неизвестными давлениями р, в фазах и скоростями фильтрации фаз u_i, появляются новые неизвестные - насыщенности s_i и концентрации отдельных компонентов. Это усложняет теоретическое исследование.