Будем для простоты рассматривать совместное изотермическое течение двух фаз в однородной пористой среде без фазовых переходов и химических реакций. Система уравнений, описывающая совместную фильтрацию фаз, строится на основе уравнений неразрывности для каждой фазы, уравнений движения (закона фильтрации) и соответствующих замыкающих соотношений.

Уравнения неразрывности

Для вывода уравнения неразрывности рассмотрим баланс вытесняющей однородной жидкости (см. гл. 3). Выделим в фильтрационном потоке элементарный объемобъём в форме прямоугольного параллелепипеда с ребрамирёбрами Dx, Dy, Dz (Рисунок - 4.4.Рисунок - 4.4.Рисунок - 4.4.Рис. 3.4). НайдемНайдём массу воды, которая входит в выделенный объемобъём вдоль оси x за время Dt. Обозначим левую и правую грани индексами 1 и 2. Через левую грань войдетвойдёт масса ( r_в u_{в x})₁ Dy Dz Dt, а через правую грань войдёет масса ( r_в u_{в x})₂ Dy Dz Dt

Рисунок - 4.4.Рис. 3.4 . Схема элемента пласта

Тогда внутри объемобъёма останется масса равная разности этих масс d m_вx. Если расстояние между гранями Δx устремить к нулю, то эта разность преобразуется к виду:

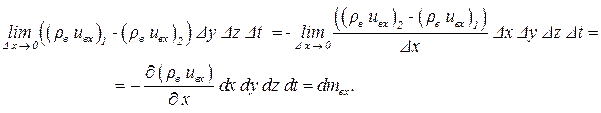
(4.13)

Аналогично можно найти массы, которые останутся внутри объемобъёма при движении вдоль осей y и z. Таким образом, общая масса оставшаяся внутри объемобъёма равна сумме этих масс

.

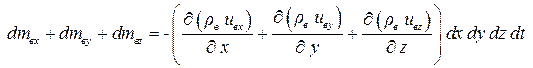(4.14)

С другой стороны масса жидкости внутри порового пространства выделенного объемобъёма равна произведению плотности r, пористости m, водонасыщенности s_в  и объемобъёма. Поэтому увеличение массы для бесконечно малого промежутка времени равно:

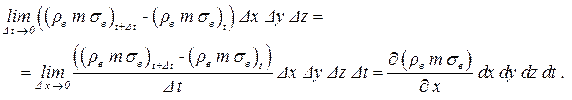
(4.15)

Прировняв эти массы и преобразовав полученное уравнение, получим дифференциальное уравнение неразрывности потока:

.

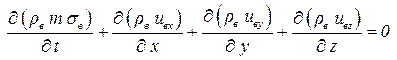(4.16)

Первое слагаемое в этом уравнении отвечает за нестационарность движения, поэтому если это слагаемое равно нулю, по движение стационарно. Остальные слагаемые отвечают за движение вдоль соответствующих осей.

Отметим, что уравнение неразрывности потока справедливо только в том случае, если поток неразрывен, то есть в потоке нет источников или стоков, выделяющих или поглощающих флюид (химических реакций, фазовых превращений и т. д.). В дивергентном виде это уравнение записывается:

.

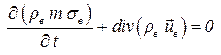(4.17)

Аналогично выводится уравнение неразрывности для нефти:

.

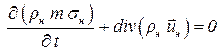(4.18)

В частных случаях уравнение упрощается. Для плоскопараллельного потока (приток к галереегалере)

.

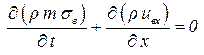(4.19)

Для плоско радиального потока (приток к скважине)

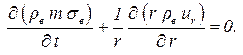
(4.20)

Для сжимаемой фазы еееё плотность, масса и насыщенность в рассматриваемом элементарном объемобъёме могут изменяться во времени. Если за некоторый промежуток времени в объемобъём втекает большеебольше массыколичество жидкости, чем вытекает, то еееё плотность и насыщенность в этом объемобъёме увеличатся (и наоборот).

Если вытесняемая и вытесняющая фазы — слабосжимаемые упругие жидкости, то влиянием сжимаемости на распределение насыщенности можно пренебречь, так как время перераспределения давления за счетсчёт сжимаемости жидкостей, по крайней мере, на два порядка меньше, чем время вытеснения. Отсюда следует, что нестационарные процессы упругого перераспределения давления заканчиваются в начале процесса вытеснения. В некоторых случаях можно считать несжимаемым и газ в пластовых условиях.

Если жидкости и пористую среду можно предполагать несжимаемыми, то уравнения неразрывности принимают вид:

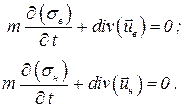
(4.21)

Теория Баклея - Леверетта

В случае одномерного течения несжимаемых несмешивающихся жидкостей в условиях, когда можно пренебречь капиллярным давлением, а также влиянием силы тяжести, процесс вытеснения допускает простое математическое описание.

Для обоих случаев одномерного потока (прямолинейно–параллельного и плоскорадиального) это приводит к классической в теории вытеснения модели Баклея—Леверетта.

Рассмотрим пласт толщиной h и длиной L Рис.Рисунок - 3.5. Слева, за границей нефтяного пласта, находится законтурная вода. Из пласта происходит отбор нефти с постоянным расходом Q_o. Вода и нефть считается несжимаемыми. В законтурной области водонасыщенность равна единице, а в нефтяном пласте вдодонасыщенность равна остаточной водонасыщенности s_во. Необходимо рассчитать распределение водонасыщенности с различные моменты времени.

Рисунок - 4.5. Рис. 3.5. Схема пласта и начальное распределение водонасыщенности

Эта задача оиписывается уравнениями неразрывности:

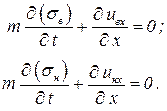
(4.22)

И обобщеннымобобщённым законом Дарси:

.

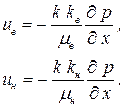(4.23)

Сложим уравнения неразрывности. Сумма насыщенностей равна единице, поэтому:

.

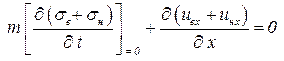(4.24)

При интегрировании последнего уравнения учтемучтём, что жидкости несжимаемые, поэтому расход отбора нефти равен расходу закачки воды. При плоско параллельном движении будут равны и скорости. Обозначим скорость внедрения воды через u_o = Q_o/(B h). Тогда:

.

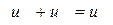(4.25)

Подставим скорости фильтрации, найденные из обобщенногообобщённого закона Дарси в последнеепоследнее уравнение:

.

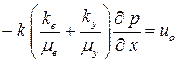(4.26)

НайдемНайдём из последнего уравнения градиент давления и подставим его в обобщенногообобщённого закона Дарси для воды:

.

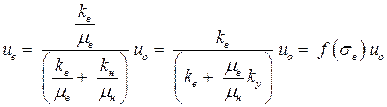(4.27)

Здесь через f(s_в) обозначена функция Баклея - Леверетта

.

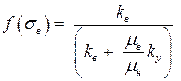(4.28)

Функция Баклея—Леверетта определяет полноту вытеснения и характер распределения насыщенности по пласту. Задачи повышения нефте – и газоконденсатоотдачи в значительной степени сворятся к применению таких воздействий на пласт, которые в конечном счетесчёте изменяют вид функции Баклея – Леверетта в направлении увеличения полноты вытеснения.

Типичные графики функции Баклея – Леверетта и еееё производной f '(s_в) изображены на рис.Рисунок - 3.6. С ростом насыщенности f(s_в) монотонно возрастает от 0 до 1. Характерной особенностью графика f(s_в) является наличие точки перегиба, участков вогнутости и выпуклости, где вторая производная f ^''(s_в) соответственно больше и меньше нуля. Эта особенность в большой степени определяет специфику фильтрационных задач вытеснения в рамках модели Баклея—Леверетта.

Рисунок - 4.6. Рис. 3.6. Типичные графики функции Баклея - Леверетта и еееё производной

Для нахождения распределения водонасыщенности по пласту подставим скорость фильтрации воды (4.26)(4.26)(4.26)(3.26) в уравнение неразрывности для воды:

.

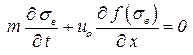(4.29)

Считая, что водонасыщенность зависит от координаты x, получим:

.

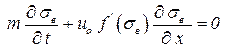(4.30)

где f '(s_в) – производная от функции Баклея – Леверетта по водонасыщенности.

Решение этого уравнения первого порядка в частных производных имеетимеет вид:

.

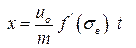(4.31)

Это решение математически справедливо рис.Рисунок - 3.7, но физически выполняется не для всех значений насыщенности. Из рисунка видно, что в каждой точке пласта будут три значения насыщенности, что абсурдно.

Рисунок - 4.7. Рис. 3.7. Распределение водонасыщенности по длине пласта

Физической особенностью модели двухфазного вытеснения Бакалея - Леверетта является зависимость скорости фильтрации воды от значения насыщенности. Действительно, из формулы (4.27)(4.27)(4.27)(3.27) и графика зависимости функции Бакалея – Леверетта от водонасыщенности следует рисунок 3.7, что с ростом водонасыщенности скорость фильтрации воды сначала растёт, а потом уменьшается.