Положение скачков (разрывов) насыщенности заранеезаранее неизвестно и должно быть найдено в зависимости от времени из решения задачи. Оказывается, что значения насыщенности и до s_- и после s₊ разрыва соответственно не могут быть произвольными, а связаны друг с другом и скоростью разрыва определеннымиопределёнными соотношениями. Несмотря на то что дифференциальное уравнение (4.22)(4.22)(4.22)(3.22), выражающеевыражающее баланс массы каждой фазы, в точках образовавшегося разрыва они теряют физический смысл, так, как производные по координате и по времени равны бесконечности.

Рассмотрим наиболеенаиболее простой случай скачка, когда водонасыщенность до скачка равна остаточной водонасыщенность s_- = s_во, а после скачка фронтальной водонасыщенности, которая неизвестна, но не меняется с течением времени s₊ = s_вф. Считая, что площадь поперечного сечения равен единице, объём закачки воды в пласта равен скорости закачки воды ,воды, а объём изменения воды в пласта равен изменению водонасыщенности в пласте умноженной на координату проникновения воды в пласт, которую можно представить в виде:

.

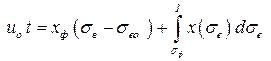(4.32)

где x_ф – координата фронта, м;

x – текущая координата положения при насыщенности s_в.

Используя формулы для положения координат точек с данной насыщенностью, получим:

.

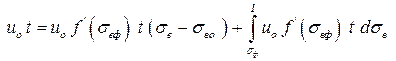(4.33)

Интегрируя и исключая постоянные множители, получим:

.

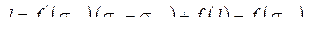(4.34)

Так, как при водонасыщенности равной единице функции Бакалея – Леверетта равна нулю, получаем уравнение:

.

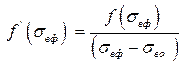(4.35)

Аналитическое решение последнего уравнения затруднительно, но  имеееёт простой геометрический смысл. Оно представляет собой уравнение касательной, проведенной из точки остаточной водонасыщенности, к кривой функции Бакалея – Леверетта, рисунок 3.8. Это даетдаёт простой графический способ определения фронтовой насыщенности по известной функции Баклея—Леверетта, который в некоторых случаях может заменить решение трансцендентного уpaвненияуравнения (4.35)(4.35)(4.35)(3.35).

Рисунок - 4.8. Рис. 3.8. Графический способ определения фронтовой и средней водонасыщенности

Важным показателем процесса вытеснения служит средняя водонасыщенность а в зоне смеси за фронтом вытеснения, определяемая как отношение объемобъёма воды в пласте после еееё закачки, к объемобъёму порового пространства в зоне смеси. Средняя водонасыщенность s_в.ср = определяется по формуле:

.

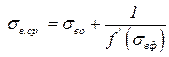(4.36)

Математическое определение фронтальной и средней насыщенности трудоёмко. Поэтому используется болееболее простой гГрафический способ определения фронтальной и средней водонасыщенности за фронтом – продолжить касательную к функции Баклея—Леверетта до точки, где функции Баклея—Леверетта равна единице. Тогда абцисса этой точки равна средней водонасыщенности за фронтом.

Равенство (4.35)(9.58) имеетимеет простую геометрическую интерпретацию. Если продолжить касательную к кривой функции Бакалея – Леверетта из точки остаточной водонасыщенности / (а) (см. рис.Рисунок – 39..48), то в точке касания выполняется условие (4.35) и по этой точке определяется фронтальная определяющую фронтовую насыщенность s_вфас, а если продолжить эту линию до значения до пересечения в точке, где функция Леверетта равна единице В с прямой / (а) = 1, то абсцисса этой точки В определит среднюю водонасыщенность за фронтомзначение а.

Необходимо отметить, что в действительности математический скачок насыщенности не имеетимеет места. Он появляется в решении вследствие пренебрежения капиллярными силами, за счетсчёт которых появляется некоторая «переходная зона» вблизи фронта вытеснения, в которой насыщенность изменяется непрерывно от значения ас до а„ (см. § 6).