Пусть в неограниченном горизонтальном пласте постоянной толщины h имеетсяимеется добывающая скважина нулевого радиуса (точечный сток). Начальное пластовое давление во всем пластево всём пласте одинаково и равно p_k. В момент времени t = 0 скважина пущена в эксплуатацию с постоянным объемобъёмным дебитом Q₀. В пласте образуется неустановившийся плоскорадиальный поток упругой жидкости. Распределение давления в пласте (в любой его точке в любой момент времени) р ( r, t) определяется интегрированием уравнения

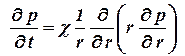.	(2.20202030)

Начальные и граничные условия задачи таковы (см. гл. 3, § 4)

р( r,0) = pk; 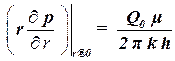. р(∞, t) = pk.

(2.21212131)

Так же, как в предыдущем случае, проведем анализ размерностей. Искомое распределение давления в пласте зависит от пяти определяющих параметров r, t, χ, р_k, и Q₀ μ/(2 π k h). ЧетвертыйЧетвёртый и пятый параметр имеетимеет размерность давления. Падение давления в пласте зависит от дебита, чем больше дебит, тем больше падение давления в пласте, поэтому будем искать решение в виде

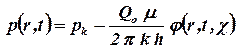.	(2.22222232)

Размерности этих аргументов таковы: [r] = L, [t] = T, [χ] = L²/T, и из них можно составить один безразмерный комплекс 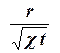. Приняв за новую переменную величину 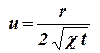, сведемсведём задачу к нахождению безразмерного давления φ, зависящего только от φ = f( u). При этом начальные и граничные условия преобразуются к виду:

t = 0, u = ∞, φ(∞) = 0; r = 0, u 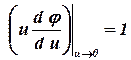= 0, ; r = ∞, u = ∞, φ(∞) = 0.

(2.23232333)

В силу линейности дифференциального уравнения (6.16) для функции Р имеемимеем такое же уравнение

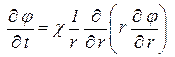
(2.24242434)

По правилу дифференцирования сложных функций находим

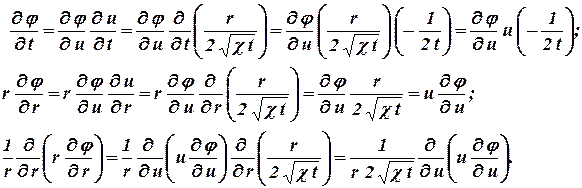
(2.25252535)

Подставляя найденные значения производных в уравнение (??.20) получим обыкновенное дифференциальное уравнение

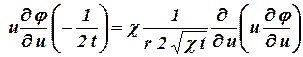,	(2.26262636)

которое можно преобразовать к виду

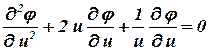.	(2.27272737)

Для решения последнего уравнения (2.27)(??.20) обозначим

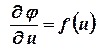, тогда уравнение (2.27)(??.20) принимает вид

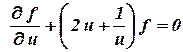.	(2.28282838)

Разделяя переменные в (2.28)(6.21) и интегрируя, получаем

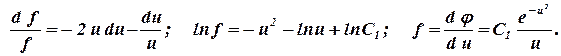
(2.29292939)

где С₁ — постоянная интегрирования. Используя граничное условие на скважине найденайдемнайдём постоянную интегрирования C₁

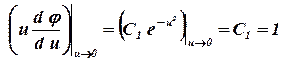.	(2.30303040)

Интегрируя (2.30)(??.22), будем иметь

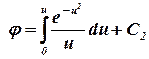.	(2.31313141)

Начальное условие и граничное условие на бесконечности одинаковы и позволяют определить Второе граничное условие и начальное условие одинаковы и позволяют определить С₂.

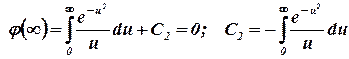.	(2.32323242)

Тогда

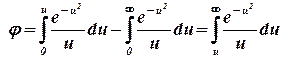.	(2.33333343)

В последнем интеграле сделаем замену 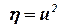, тогда  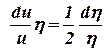и решение преобразуется к виду

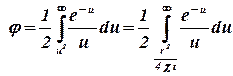.	(2.34343444)

Интеграл в (2.34)(??.27) называется интегралом вероятности и является табулированной функцией, изменяющейся в пределах от 0 до - ∞001.

Тогда закон распределения давления при неустановившемся фильтрационном потоке упругой жидкости к скважине работающей с постоянным расходом приимеетпримет вид

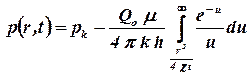.	(2.35353545)

Формула (1.45) получила название основной формулы теории упругого режима фильтрации. Она имеетимеет широкое практическое применение, и в частности используется при интерпретации результатов исследования скважин.

Интеграл в основной формулыв основные формулы теории упругого режима называется интегральной показательной функцией и обозначается

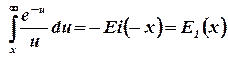.	(2.36363646)

При малых значениях аргумента x << 1 интегральная показательная функция имеетимеет простую асимптотику:

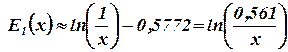.	(2.37373747)

Поэтому при выполенениивыполнении условия 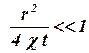 давление в любой точке пласта можно рассчитывать по приближенной формуле

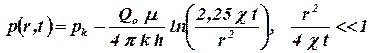.	(2.38383848)

На рисунке .5 показан вид интегральной показательной функции и еееё ассимптотика при малых значениях аргумента. При значениях аргумента x = 0,01 погрешность составляет 2.3%.

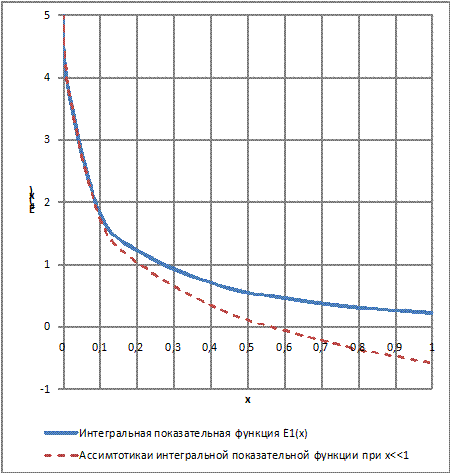Рисунок - 2.11117. График интегральной показательной функции и еёе асимптотики при малых аргументах Рис. 1.7

Типичные кривые распределения давления в различные моменты времени при пуске сквожиныскважины с постоянным расходам показаны на рис.Рисунок - 2.12Рисунок - ??.1. На рисунке Рисунок - 2.13??.3 показано изменение давления в различных точках пласта с течением времени.

Расход жидкости через любую цилиндрическую поверхность радиусом r и скорость фильтрации мажноможно найти из закона Дарси

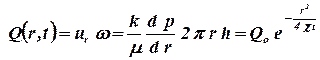.	(2.39393949)

Строго говоря, основная формула теории упругого режима (1.48) справедлива лишь для случая точечного стока (при r_с → 0) в неограниченном пласте.

В заключение приведёем пьезометрические кривые для бесконечного пласта, который эксплуатируется скважиной радиуса r_с с постоянным дебитом Q_o (рис.Рисунок - 2.12Рисунок - 6.4). Для точек вблизи забоя можно пользоваться формулой (1.7): дифференцируя еееё по координате r, найдемнайдём градиент давления

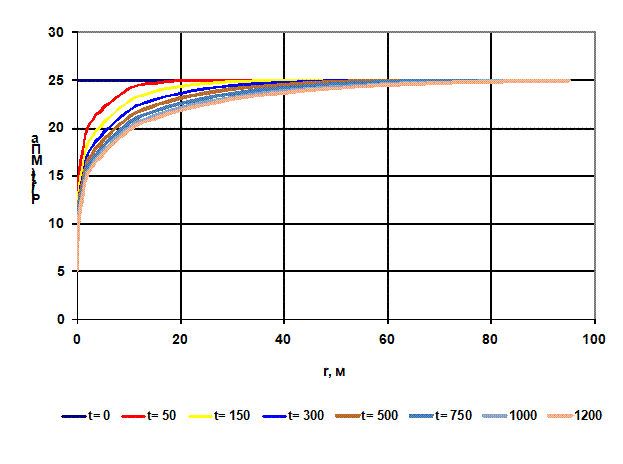Рисунок - 2.12128. Кривые распределения давления вокруг скважины в различные моменты Рис. 1.8

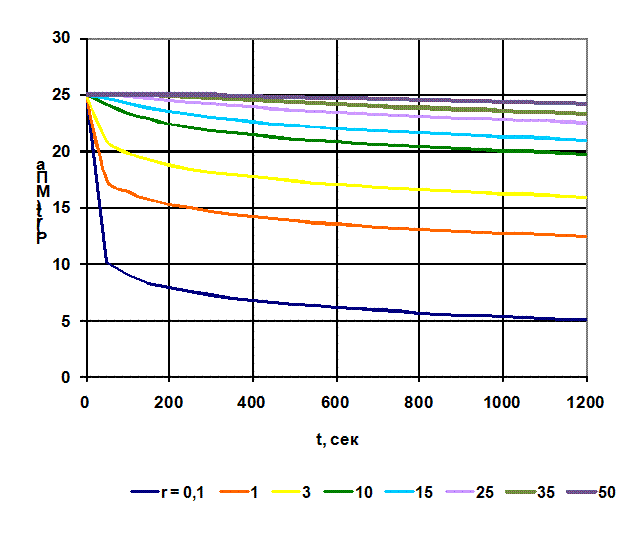Рисунок - 2.13139. Изменение давления в различных точках скважины с течением времени Рис. 1.9

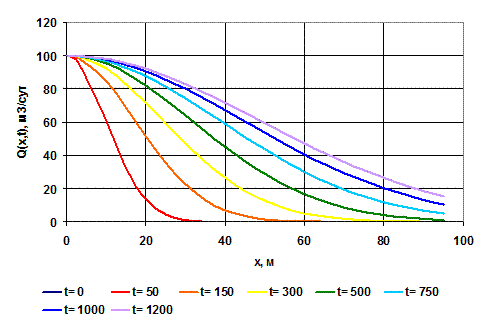Рисунок - 2.141410.Рис. 1.10. Кривые распределения дебита вокруг скважины в различные моментына различных расстояниях от галереи

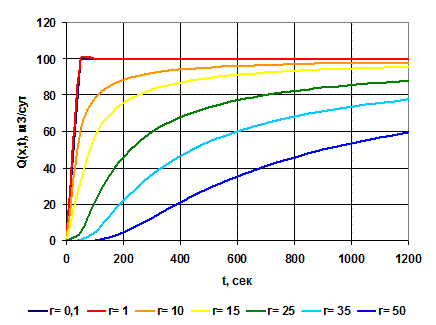Рисунок - 2.151511.Рис. 1.11. Кривые изменения дебита в различных точках с течением времени

Для указанных значении r пьезометрические кривые представляют собой логарифмические линии (см. рис.Рисунок - 1.7). Углы наклона касательных на забое скважины одинаковы для всех кривых.