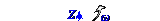
Элементарная δ A работа, выполненная вектором M_Oвн главного момента сил, при повороте твёрдого тела на dφ элементарный вектор угла вокруг OZ оси вращения приведет к приращению

 dW _k кинетической энергии тела, которое имеет по аналогии с (1.87) следующий вид:

                   δ A = dW_k                                                                                                         W_k2        φ₂

                   dW_k = M_Oвн dφ « dW_k = M_Oвн dφ « dW_k = M_OZвн dφ « ∫ dW_k =∫ M_OZвн dφ «

                                                                                                             W_k1 φ₁       φ₂

                                                                                                   « ΔW_k = W_k2 - W_k1 = ∫ M_OZвн dφ,       (1.92)                                                                                                              φ₁

где M_OZвн  - проекция вектора M_Oвн главного момента от всех векторов F_i  внешних сил на OZ ось вращения твёрдого тела, по которой направлен dφ элементарный вектор угла поворота;

φ₁, φ₂ - начальное и конечное значения угла поворота твёрдого тела вокруг OZ оси вращения;

       n

где M_O = ∑[r_i,F_i ] - главный(1.58) момент от n векторов F₁, F₂, …, F_n сил  относительно О полюса,

        i = 1

находящегося на OZ оси вращения твёрдого тела, а r_i  - радиус - вектор, проведённый из О полюса в точку приложения векторов F_i  внешних сил.

       Выражение (1.92) - это теорема о кинетической энергии, согласно которой

 ΔW_k = W_k2 - W_k1  приращение кинетической энергии равно работе M_Oвн главного момента от 

n векторов F₁, F₂, …, F_n сил  относительно О полюса, находящегося на OZ оси вращения этого твёрдого тела.

       Согласно (1.92) при M_OZвн < 0, т.е. отрицательного значения проекции вектора M_Oвн главного момента от n векторов F₁, F₂, …, F_n сил  относительно О полюса, находящегося на OZ оси вращения  твёрдого тела, ΔW_k = W_k2 - W_k1  приращение кинетической энергии этого твёрдого тела отрицательно. При (1.92)  M_OZвн > 0 приращение ΔW_k = W_k2 - W_k1  кинетической энергии твёрдого тела положительно.

       Из (1.92) получаем следующее выражение:

δ A = dW_k = M_Oвн dφ = (M_Oвнω) dt = (M_OZвнω) dt = J_OZβωdt = J_OZ( dω/ dt)ωdt = J_OZωdω = J_OZωdω,           (1.93) где ω = dφ/ dt - вектор ω угловой скорости вращения твёрдого тела вокруг OZ оси, равный согласно (1.18) отношению вектора dφ элементарного приращения угла поворота твёрдого тела к элементарному dt промежутку времени, в течение которого длился этот поворот; M_Oвн - вектор главного момента от всех векторов F внешних сил, приложенных к твёрдому телу относительно      O полюса, находящегося на OZ оси вращения твёрдого тела; M_OZвн - составляющая вектора

M_Oвн главного момента  от всех векторов F внешних сил, приложенных к твёрдому телу, направленная по OZ оси вращения; (M_Oвнω) = M_Oвн ωcosα и (M_OZвнω) = M_OZвн ω = M_Oвн ωcosα - равные скалярные произведения, поскольку составляющая M_OZвн вектора M_Oвн, направленная по OZ оси вращения, определяется из выражения:   M_OZвн = M_Oвн cosα, где α - угол между вектором M_Oвн и OZ осью;

M_OZвн = J_OYβ - согласно (1.76) уравнению динамики  твердого тела вектор M_OZвн главного момента внешних сил пропорционален вектору β углового ускорения вращения твердого тела относительно неподвижной OZ оси; β = dω/ dt - вектор β углового ускорения вращения твёрдого тела вокруг OZ оси, равный согласно (1.21) отношению элементарного приращения вектора dω угловой скорости при вращении твёрдого тела вокруг OZ оси к элементарному dt промежутку времени, в течение которого это приращения вектора dω угловой скорости произошло.

       Кинетическая энергия W_k (рис.1.21), вращающегося твёрдого тела вокруг OZ оси под воздействием вектора M_Oвн главного момента от всех приложенных к твёрдому телу относительно

O полюса векторов F_i внешних сил, в данный момент t времени, когда модуль вектора ω угловой скорости вращения достигнет ω значения, имеет по аналогии с (1.89) следующий вид:

                                                                                            W_k        ω                                                                                                                                   W_k =∫ dW_k = ∫ J_OZωdω = ( J_OZω²)/2.               (1.94)                                                                                                                    0      0