Инерциальной системой отсчета (ИСО) называется такая, в которой материальная точка, свободная от внешних воздействий, покоится или движется равномерно и прямолинейно. Экспериментально установлено, что практически инерциальна гелиоцентрическая система отсчета, начало координат которой находится в центре масс Солнечной системы, т.е. на Солнце, а оси проведены в направлении трех удаленных звезд, выбранных так, чтобы оси координат были взаимно перпендикулярны.

       Содержание первого закона Ньютона сводится к двум утверждениям: во-первых, что существуют ИСО и во-вторых, что все тела обладают свойством инертности.

       Второй закон Ньютона в ИСО гласит: dp / dt первая призводная от вектора p импульса материальной точки или механической системы по t времени равен действующему на нее вектору F силы, которое с учётом (1.12) вектора a мгновенного ускорением материальной точки и постоянства m массы имеет место следующий вид: dp / dt = F ↔ d( mv)/ dt = F ↔ ma = F,     (1.42)

где m, v и a = dv/dt = d²r/dt² соответственно масса, векторы скорости и ускорения материальной точки или механической системы; r  - ее радиус - вектор.

       Вторая формулировка второго закона Ньютона гласит: вектор a ускорения материальной точки или механической системы совпадает по направлению с действующим на нее вектором F силы и равен отношению этого вектора F силы к m массе материальной точки.

       Вектором Fdt импульса силы   называется произведение вектора F силы на элементарный   dt промежуток времени, в течение которого этот вектор F силы действует на  материальную точку или механическую систему. Согласно второму закону Ньютона (1.42) элементарное приращение вектора dp импульса за dt элементарный промежуток времени материальной точки или механической системы равно вектору Fdt импульса силы, действующему за этот dt элементарный промежуток времени на  эту материальную точку или механическую систему.                                          

       Приращение вектора Δp импульса материальной точки или механической системы за интервал времени Δ t = t₂ - t₁ времени, за который произошло это приращение вектора Δp импульса материальной точки или механической системы, с учётом (1.42) имеет следующий вид:                                                                                                                 t₂                t₂  

                                                    dp = Fdt ↔ Δp = p₂ - p₁ ↔ Δp = ∫dp ↔ Δp = ∫Fdt,            (1.43)

                                                                                                  t₁            t₁            

где p₁ и p₂ - векторы импульсов материальной точки или механической системы  соответственно в момент t₁ времени начала и в момент t₂ времени окончания действия вектора F силы, действующего на эту материальную точку или механическую систему.

       Если на материальную точку m массой одновременно действуют несколько векторов F₁, F₂, …, F_n сил, то её вектор a ускорения  с учетом выражения (1.36) равнодействующего вектора силы имеет следующий вид:                                                                           n   n       n

                                                                                                  a = (∑F_i)/m =∑F_i/m =∑a_i.    (1.44)                                                                                         i = 1   i = 1  i = 1

       Согласно принципу независимости действия сил каждый из векторов F₁, F₂, …, F_n сил, одновременно действующих на материальную точку или механическую систему, сообщает ей такое же ускорение a₁ = F₁/ m, a₂ = F₂/ m,…, a_n = F_n/ m, как если бы других сил не было.

       Подставляем  (1.12) вектор a мгновенного ускорением материальной точки или механической системы  во (1.42) второй закон Ньютона в ИСО и получаем выражение связи вектора a ускорения материальной точки или механической системы  m массой с вектором          (рис. 1.12)

F_р равнодействующей силы, приложенной к этой материальной точке или механической системе, которое учетом выражения (1.36) равнодействующего вектора силы имеет следующий вид:

     n

                                                                                                         ma = m(d²r/dt²) = F _р = ∑F_i.     (1.45)

                                                                                                                                 i = 1

       Дифференциальное уравнение (1.45) движения материальной точки или механической системы m массой  с учётом F_{р x}, F_{р y} и F_{р z} проекций на оси прямоугольной декартовой системы координат вектора F_р равнодействующей силы, а также с учетом (1.13) проекций a_x, a_y и a_z как вторых d² x/ dt², d² y/ dt² и d² z/ dt² производных x, y и z координат этой движущейся под действием вектора                     F_р равнодействующей силы материальной точки или механической системы  m массой, имеет следующий вид:          m( d² x/ dt²)i + m( d² y/ dt²)j + m( d² z/ dt²)k = F_{р x}i + F_{р y} j + F_{р z}k ↔

                                                        ↔ m( d² x/ dt²) = F_{р x}; m( d² y/ dt²) = F_{р y}; m( d² z/ dt²) = F_{р z}.     (1.46)

       Если F_ik - вектор силы, действующий на i - ую материальную точку механической системы со стороны k-ой материальной точки, а F_ki - вектор силы, действующий на k-ую материальную точку со стороны i-ой, то согласно третьему закону Ньютона (рис. 01.0.14) имеет место следующее выражение:

                                                                                                                                   F_ik = -F_ki.   (1.47)

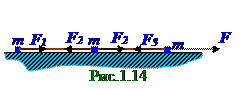
вследствие чего имеет место следующее выражение:                            n   n                                                                                                                                                 ∑  ∑F_ik = 0,        (1.48)

                                                                                                             i = 1  k = 1

где n - число материальных точек, входящих в состав механической системы, а F_ii = 0.                 Для (рис.1.14) случая движения брусков под воздействием вектора F внешней силы, связанных между собой нерастяжимой невесомой нитью, по гладкой поверхности внутренними силами являются силы натяжения нити между соседними брусками. Силы натяжения нитей между соседними брусками являются внутренними силами, вследствие чего имеет место следующее выражение:                                                                                                                      F₁₂ = - F₂₁; F₂₃ = -F₃₂.           (1.49)

       С учетом F₁₁ = 0, F₂₂ = 0, F₃₃ = 0, а также пренебрегая гравитационным взаимодействием между брусками m₁, m₂ и m₃ массы, выражение (1.48) для рис.1.14 принимает следующий вид:

                                                                                                            F₁₂ + F₂₁ + F₂₃ + F₃₂ = 0. (1.50)

1.2. Лекция 3. Закон сохранения импульса.