Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

           

       Положение тела в пространстве можно определить только по отношению к другим телам. Например, имеет смысл говорить о положении планеты по отношению к Солнцу, самолета или теплохода по отношению к Земле, но нельзя указать их положение в пространстве "вообще", безотносительно к какому-либо конкретному телу.

       Абсолютно твердое тело, с которым жестко связана система координат, снабженная часами и используемая для определения положения в пространстве исследуемых тел и частиц в различные моменты времени, называется системой отсчета.

       Наиболее употребительна прямоугольная декартова система координат, ортонормированный базис которой образован тремя единичными по модулю и взаимно ортогональными векторами i, j и k, проведенными из O начала координат. Положение материальной M точки  характеризуется r радиусом - вектором, соединяющим O начало координат с этой M точкой.

Вектор r раскладывается по базису i, j и k, вследствие чего имеет место следующее выражение:              r = xi + yj + zk,                              (1.1) где xi,  yj и zk - составляющие r вектора по осям координат. Коэффициенты разложения x, y и z представляют собой декартовы координаты M точки, называемые также (рис. 1.1) координатами

                                                                                                                                 

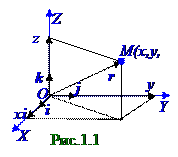
r радиуса - вектора. В силу ортогональности векторов i, j и k базиса координаты x, y и z равны проекциям r радиуса - вектора на соответствующие оси координат.

           

Кинематика материальной точки и абсолютно твердого тела: кинематические уравнения движения; траектория; путь и перемещение; мгновенные скорость и ускорение при прямолинейном и криволинейном движении; центр кривизны; угловая скорость, нормальное и тангенциальное ускорения при вращательном движении

    Движение материальной точки полностью определено, если заданы три непрерывные и однозначные функции t времени, т.е. имеют место следующие выражения:      x= x( t), y= y( t) и z= z( t),    (1.2)                                                         описывающие изменение координат точки со t временем. Эти уравнения называются кинематическими уравнениями движения материальной точки или параметрическими уравнениями.

       Вектором Δr перемещения (рис. 1.2) за промежуток времени от t= t₁ до t= t₂ называется вектор, проведенный из положения M материальной точки в t₁момент в ее положение в t₂ момент времени. Длина пути ΔS, пройденного M материальной точкой из ее начального положения, является скалярной функцией t времени ΔS, причем ΔS является положительной величиной. При движении

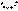M материальной точки по дуге      T траектории из 1 положения в 2 положение за Δ t = t₂ - t₁ промежуток времени она проходит путь ΔS = 12. Радиусы - векторы r₁ и r₂, характеризующие положения M материальной точкой соответственно в моменты t₁, t₂ времени, когда она находится соответственно в1 и 2 положениис учетом (1.1) имеют следующие значения:                                                                                                r₁ = x₁i + y₁j + z₁k; r₂ = x₂i + y₂j + z₂k.         (1.3)          

 

Согласно определению вектора Δr перемещения как разности r2 - r1 соответственно r2 конечного и r1 начального радиусов - векторов, а также с учётом (1.3) имеет место следующее выражение:                                         Δr = r2 - r1 = ( x2 - x1)i + ( y2 - y1)j + ( z2 - z1)k = Δr = Δxi + Δyj + Δzk. (1.4)

      

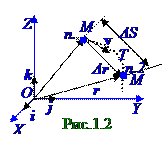
       Мгновенной скоростью M материальной точки (рис.1.2) называется v векторная величина, равная первой производной по t времени от r вектора перемещения рассматриваемой точки и имеющая следующее значение:                                                                       v = limΔr /Δ t = dr / dt.    (1.5)                                                                                                                            Δ t→0      

       При стремлении промежутка Δ t = t₁ - t₂  времени  к нулю, за который (рис.1.2)

M материальная точка

перемещается из 1 в 2 положение, модуль Δr  вектора Δr перемещения стремится к приращению ΔS пути, вследствие чего имеет место следующее выражение:          

                                                                                                     limΔr = limΔS ↔ dr = dS. (1.6)                                                                                             Δ t→0 Δ t→0

       Подставляем (1.6) в (1.5) и получаем следующее выражение модуля v вектора v мгновенной скорости M материальной точки, который равен первой производной от S длины пути по t времени:

                                                                    v = lim ΔS/Δ t = lim Δr/Δ t ↔ v = dr/ dt = dS/ dt.  (1.7)                                                                           Δ t→0     Δ t→0                                            

       Подставляем (1.1) в (1.5) и получаем (рис. 01.0.3) следующее выражение вектора v скорости

M материальной точки в прямоугольной (рис.1.1) системе координат, начало O координат которой совмещено с этой M материальной точки:

Модуль v вектора v скорости M материальной точки (рис. 01.1.3) имеет следующий вид:            v = (vx 2+ vy 2 + vz 2)1/2 .          (1.10) Производим интегрирование в(1.7) и получаем следующее выражение S пути:

                                          v = d( xi + yj + zk)/ dt = (dx/ dt)i + ( dy/ dt)j + (dz/ dt)k =  v_xi + v_yj + v_z k      (1.8)       Проекции v_x, v_y, v_z вектора v мгновенной скорости M материальной точки (рис.1.3) на оси координат имеет с учетом (1.8) следующий вид:                        v_x = dx/ dt; v_y = dy/ dt; v_z = dz/ dt.           (1.9)                

                                                                                                                     t₂

                                                                                                  dS = vdt ↔ S = ∫v dt.            (1.11)                                                                                                                       t₁

       Согласно (1.11) S путь, проходимый M материальной точки за от t₁ до t₂ промежуток времени, равен определенному интегралу от модуля v вектора v скорости по t времени.

       Для характеристики быстроты изменения вектора v скорости  точки в механике вводится понятие ускорения. Мгновенным ускорением точки называется a векторная величина, равная первой производной по t времени от вектора v скорости рассматриваемой M материальной точки или с учетом (1.5) - второй производной по t времени от r радиуса - вектора этой M материальной точки, вследствие чего имеет место следующее выражение:                    a = dv/ dt = d²r/dt².             (1.12)

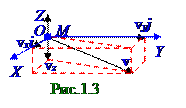
       Подставляем (1.1) в (1.12) и получаем выражение вектора a ускорения перемещающейся                   M материальной точки как функцию от d² x/ dt², d² y/ dt² и d² z/ dt² вторых производных                      x, y и  z координат этой перемещающейся M материальной точки по t времени, как функцию от dv_x / dt, dv_y / dt и dv_z / dt первых производных по t времени (рис.1.3) проекций v_x, v_y и v_z вектора v скорости на оси координат, а также получаем следующее выражение вектора a ускорения как функцию от проекций a_x, a_y и a_z этого вектора a ускорения перемещающейся M материальной точки на оси прямоугольной (рис.1.1) системы координат :

       a = d²( xi + yj + zk)/ dt²=( d² x/ dt²)i + ( d² y/ dt²)j + ( d² z/ dt²)k = ( dv_x / dt)i + ( dv_y / dt)j + ( dv_z / dt)k =                                                                                                              = a_xi + a_yj + a_zk,                 (1.13)

где a_x = dv_x / dt = d² x/ dt²; a_y = dv_y / dt = d² y/ dt²; a_z = dv_z / dt = d² z/ dt².

       Модуль a вектора a ускорения по аналогии с (1.10) имеет с учетом (1.13) следующий вид:

a = ( a_x²+ a_y² + a_z²)^1/2 = [(dv_x/dt)² + (dv_y/dt)² +(dv_z/dt)²]^1/2  =  [(d²x/dt²)² + (d²y/ dt²)² +(d²z/ dt²)]^1/2. (1.14)

При прямолинейном (рис. 01.0.4) движении M материальной точки с изменяющимся во t времени модулем v вектора v скорости v1, v2, v3, … в моменты t1, t2, t3, …времени

      

соответственно существует только вектор a_τ тангенциального  ускорения, направленный по

τ единичному вектору и имеющий следующий вид:                                         a_τ = (dv/ dt)τ,   (1.15) где τ = v/v - единичный вектор, направленный по вектору v скорости; dv/ dt = a_τ – проекция вектора 

a_τ тангенциального  ускорения на направление τ единичного вектора.

       При равномерном (рис.1.5) движении M материальной точки по окружности R радиуса с

O центром с постоянным по v_τ модулю   вектором v_τ линейной скорости, направленным по касательному к окружности τ единичному вектору, меняется только направление этого  вектора

по касательному к окружности τ единичному вектору, меняется только направление этого  вектора

v_τ линейной скорости. В этом случае (рис.1.5) M материальная точка имеет только

Z

вектор an нормального ускорения, определяемый следующим выражением:         an =( vτ2/ R)n,        (1.16) направленный к центру окружности R радиусом по       n единичному вектору.

                                                

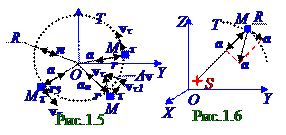
       В общем случае (рис.1.6) при T криволинейной траектории движения M материальной точки, имеющей в произвольный момент времени S центр R_S  радиуса кривизны траектории, с переменным по времени вектором v_τ тангенциальной скорости вектор a ускорения раскладывается на две взаимно перпендикулярные составляющие, вследствие чего имеет место следующее выражение:                                                                                                                                             a = a_τ + a_n,                       (1.17) где a_τ - вектор тангенциального ускорения и a_n - вектор нормального ускорения.

Поступательным движением твердого тела называется такое его движение, при котором любая прямая, жестко связанная с телом, например, АВ прямая  на рис.1.7, перемещаясь с телом, остаётся параллельной своему первоначальному А0 B0 направлению. Поступательно движутся относительно Земли, например, кабина.

A

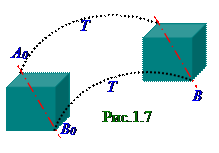
лифта, резец токарного станка. Кинематическое рассмотрение поступательного движения твердого тела сводится к изучению движения любой из его точек.

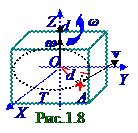
       Движение твердого тела, при котором точки, находящиеся (рис. 1.8) на OZ оси, неподвижны, называется вращением тела вокруг этой неподвижной OZ оси.                                   Вектором угловой скорости вращения твердого тела вокруг, например, неподвижной OZ оси называют вектор ω, который равен первой производной от вектора φ угла поворота A точки этого твердого тела по t времени и направлен вдоль неподвижной OZ оси вращения так,     , чтобы из его                     

конца вращение тела было видно происходящим против часовой стрелки, поэтому для вектора ω угловой скорости имеет место следующее выражение:                                                                                              ω= dφ/ dt.      (1.18) Вращение тела называется равномерным, если модуль  ω вектора ω угловой скорости не изменяется с течением времени, т.е.  ω= const.

 

       Равномерное вращение характеризуется T периодом обращения, под которым понимают время, за которое тело поворачивается на 2π угол. С учетом (1.18) модуль  ω вектора ω угловой  скорости при равномерном вращении, который называют также циклической частотой вращения имеет следующий вид:                                                                                                 ω =2π/ T.                   (1.19)

       Число оборотов в единицу времени или n частота вращения с учетом (1.19) имеет следующий вид:                                                                                               n = 1/ T = ω/2π,                  (1.20) где модуль ω вектора ω угловой  скорости равномерного вращения равен φ углу поворота тела в радианах за единицу времени.

       Вектор ω угловой  скорости вращения может изменяться как за счет уменьшения или увеличения его ω модуля, так и за счет переориентации направления этой оси вращения в пространстве. Пусть за Δ t время вектор ω угловой  скорости вращения получает Δω приращение, тогда вектор β углового ускорения определяется следующим выражением:

                                                                                                                 β = lim(Δω/Δ t) = dω/ dt. (1.21)                                                                                                                         Δ t→0

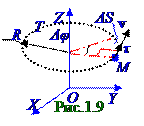
       Отдельные точки вращающегося твердого тела (рис. 01.0.8) имеют различные векторы v_τ линейной скорости, которые непрерывно изменяет свое направление. Пусть за малый Δ t промежуток времени (рис.1.9) M материальная точка твердого тела повернулась по Т  траектории вокруг OZ оси вращения, представляющей собой окружность R радиуса, на Δφ угол, вследствие чего эта M материальная точка проходит путь ΔS, определяемый из следующего выражения: ΔS = RΔφ.      (1.22)

Модуль vτ вектора vτ линейной скорости, направленным (рис.1.9) по касательному к окружности τ единичному вектору, с учетом (1.7) и (1.22) связан с модулем ω вектора ω угловой скорости при движении M материальной точки по окружности R радиуса следующим выражением:                                        vτ = lim( ΔS/Δ t) = lim( RΔφ/Δ t) = Rdφ/ dt = ω R.           (1.23)                                     Δ t→0        Δ t→0

                                                    

       Положение рассматриваемой A точки вращающегося вокруг OZ оси неподвижной OZ оси твердого тела с вектором ω угловой  скорости определяется r радиусом - вектором, проведенным в эту A точку  из (рис.1.10) O начала координат.

Модуль |[ ω, r]|  векторного произведения [ω, r] имеет следующий вид:                                             |[ ω, r]| =  ω rsinα =  ω R,             (1.24) где R - радиус окружности, по которой движется A точка, α - угол между вектором ω угловой скорости вращения тела и r радиусом - вектором.

                                                             

Y

                                                                 

       Согласно (рис.1.9) вектор v_τ линейной скорости, направленный  по касательному к окружности τ единичному вектору, находится в плоскости окружности и перпендикулярен (рис.1.10) R радиусу этой окружности, по которой вращается либо (рис.1.9) M материальная точка, либо (рис.1.10) A точка твердого тела. Радиус R пересекает (рис.1.10) OZ ось вращения в B точке. На этой же OZ оси находится O точка - начало координат, поэтому r радиус - вектор, направленный из O начала координат в       (рис.1.10) A точку твердого тела, OZ ось вращения, по которой направлен вектор ω угловой  скорости вращения твердого тела, и R радиус находятся в одной плоскости. Поэтому (рис.1.10) вектор v_τ линейной скорости перпендикулярен плоскости, образованной векторами ω угловой  скорости и r радиус - вектор, вследствие чего с учетом (1.24) векторное произведение [ω, r] имеет следующий вид:

                                                                                 [ ω, r] = v_τ ↔ |[ ω, r]| =   ω R = v_τ.          (1.25) т.е. вектор v_τ линейной скорости данной точки твёрдого тела, вращающегося вокруг, например,

(рис.1.10) OZ оси, с вектором ω угловой  скорости, равен векторному произведению вектора              ω угловой  скорости вращения и r радиус - вектора, проведённого из O начала координат, лежащей на OZ оси вращения, в эту точку твёрдого тела.                       

       Вектор v_τ линейной скорости (рис.1.10) точки твёрдого тела, вращающегося вокруг неподвижной оси, перпендикулярен плоскости, образованной вектором ω угловой  скорости и

r радиусом - вектором (рис.1.10) точки этого твёрдого тела и направлен в сторону, чтобы из окончания вектора v_τ линейной скорости вращение вектора ω угловой  скорости до совмещения с

r радиусом - вектором по кратчайшему пути было видно против вращения «часовой стрелки». Иначе говорят, что векторы ω, r и v_τ образуют правую тройку векторов.                                                                Модуль (рис.1.5) a_n вектора a_n нормального ускорения из (1.16) с учетом (1.23) связан с квадратом ω² модуля ω вектора ω угловой  скорости вращения материальной точки по окружности  R радиуса следующим выражением:                                                   a_n =  v_τ²/ R = ω²R.            (1.26)

       С учетом (1.26), (рис.1.10) противоположности направления вектора R радиуса, проведённого из центра B окружности в A точку, вектору a_n нормального ускорения выражение для этого вектора a_n нормального ускорения принимает следующий вид: a_n = - ω²R = (v_τ²/ R)n,       (1.27) где n - единичный вектор, коллинеарный вектору a_n нормального ускорения и направленный с ним в одну сторону.                                                                              

       Модуль ω вектора ω угловой  скорости с учётом (1.23) имеет следующий вид: ω = v_τ/ R. (1.28)

       Подставляем (1.28) в (1.21) и получаем следующее выражение связи модуля β вектора

β углового ускорения с модулем v_τ вектора v_τ линейной скорости при вращении (рис.1.10) твердого тела вокруг неподвижной оси:                                                                        β = ( dv_τ/dt)/ R.      (1.29)

       С учетом (1.15) связи модуля v_τ  вектора v_τ тангенциальной скорости и модуля a_τ вектора    a_τ тангенциального ускорения выражение (1.29) принимает следующий вид:

                                                                                                     β = a_τ/ R ↔ a_τ = β R,                      (1.30) т.е модуль a_τ вектора a_τ тангенциального  ускорения любой точки твёрдого тела, вращающегося вокруг некоторой оси с модулем β вектора β углового ускорения, равна произведению этого модуля β  вектора β углового ускорения на R радиус окружности, по которой вращается эта любая точка твёрдого тела.