С учетом (1.12), (1.68) первая производная по t времени  от результирующего (1.68) вектора L_O момента импульса  механической системы относительно любого O полюса  равна вектору    M_Oвн главного момента сил (1.58) от всех векторов F_i внешних сил, приложенных к этой механической системе, относительно того же O полюса, вследствие чего имеет место следующее выражение:                                                               n               n                    n          n

                                     dL_O / dt = d∑ [r_i,m_iv_i ]/ dt = ∑[r_i,m_i dv_i ]/ dt = ∑[r_i,m_i a_i] = ∑[r_i,F_i] = M_Oвн, (1.69)                                            i = 1             i = 1          i = 1    i = 1

где  m_i, r_i , v_i и a_i - соответственно масса, радиус - вектор, векторы скорости и ускорения i-ой материальной точки, а n - общее число точек в системе.       

       Уравнение (1.69) является уравнением моментов для тела, вращающегося вокруг полюса, т.е. неподвижной точки, в инерциальной системы отсчёта.

       В проекциях на оси неподвижной прямоугольной декартовой системы с O началом координат уравнение моментов твердого тела, вращающегося вокруг этого O начала координат, которое совпадает с O полюсом, имеет следующий вид:       

                                                                             dL_x/ dt = M_xвн; dL_y/ dt = M_yвн; dL_z/ dt = M_zвн, (1.70)

где L_x, L_y, L_z  и M_{x вн}, M_{у вн}, M_zвн - соответственно (1.68) проекции результирующего вектора  L_O момента импульса механической системы и (1.58) проекции вектора M_Oвн главного момента от всех векторов F_i внешних сил на оси неподвижной прямоугольной декартовой системы с O началом координат.

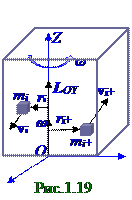
        Тело вращается (рис. 1.19) вокруг неподвижной OZ оси. Направление его результирующего (1.68) вектора L_OZ момента импульса совпадает с направлением этой неподвижной OZ оси. С учетом векторов ω угловой  скорости каждой элементарной m_i массы этого тела с r_i радиусом - вектором, перпендикулярным неподвижной OZ оси, и равенства согласно (1.25) вектора v_i линейной скорости  каждой части тела v_i =[ω,r _i], а также с учетом  (1.68) результирующий вектор L_OZ момента импульса относительно неподвижной OZ оси имеет следующий вид:

                                                                                                       n               n

                                                                                           L_OZ = ∑ [r_i,m_iv_i] = ∑ [r_i,m_i[ω,r_i]].    (1.71)                                                                                              i = 1        i = 1                              Двойное векторное произведение в (1.71) с учетом скалярного произведения (r_iω) = 0, т.к. (рис.1.19) r_i радиус – вектор перпендикулярен вектору ω угловой  скорости, имеет следующий вид:

       Подставляем в (1.73) выражение (1.63) момента инерции J _OZ  тела относительно неподвижной OZ оси и получаем следующее выражение результирующего вектора L_OZ момента импульса с вектором ω угловой  скорости вращения этого твёрдого тела вокруг неподвижной OZ оси:

                                                                                                                                        L_OZ = J _OZω.     (1.74) Берём первую производную по t времени от левой и правой частей (1.74), подставляем в полученное выражение (1.21) вектор β  углового ускорения при вращении твёрдого тела и получаем следующее выражение первой производной по t времени от результирующего вектора L_OZ момента импульса относительно неподвижной OZ оси:                     dL_OZ/ dt = J_OZ( dω/ dt) = J_OZβ.  (1.75)

       Вращение механической системы относительно неподвижной OZ оси является частным случаем вращения этой механической системы вокруг O полюса, лежащего на неподвижной OZ оси. С учётом этого левые части выражений (1.69) и (1.75) равны друг другу. Поэтому можно приравнять правые части выражений (1.69) и (1.75), но заменить в правой части выражения (1.69) вектор M_Oвн главного момента (1.58) от всех векторов F_i внешних сил, приложенных к механической системе, относительно O полюса вектором M_OYвн главного момента  от всех векторов F_i внешних сил, приложенных к механической системе, относительно неподвижной OZ оси, вследствие чего имеет место следующее выражение:                                                                                                   dL_OZ/ dt = J_OZβ = M_OZвн,           (1.76) которое определяет изменение момента импульса механической системы в произвольный момент

t времени и является уравнением динамики  твердого тела, вращающегося вокруг неподвижной оси, согласно которому вектор M_вн главного момента внешних сил, направленного по этой оси, пропорционален вектору β углового ускорения вращения твердого тела относительно неподвижной оси.