Пусть инвестор распределяет свой капитал среди N ценных бумаг в некоторых пропорциях 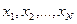. Предполагается, что P_ij и доходности R_ij являются случайными величинами. За один период t можно сформировать вектор доходностей  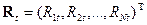и вектор, определяющий структуру портфеля .

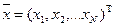Решение задачи формирования оптимального портфеля основано на предположениях относительно:

· вероятностной модели доходностей;

· рынка и поведения его участников.

В качестве первой модели оцениваются статистические параметры выборочного среднего 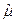, выборочной ковариационной матрицы 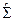, и они рассматриваются как прогнозы характеристики будущих периодов.

Предположения относительно поведения рынка и его участников состоит в следующем:

1. Инвесторы осуществляют оценку портфеля, основываясь на ожидаемой доходности и риске активов.

2. При выборе из двух идентичных портфелей инвестор отдает предпочтение портфелю с большей ожидаемой доходностью и с меньшим риском.

3. Характеристики активов и портфелей относятся к одному заданному периоду владения.

4. Активы являются бесконечно делимыми, т.е. в каждый актив может быть вложена любая доля капитала инвестора.

5. Отсутствуют технические препятствия в реализации оптимальных инвестиционных стратегий; относительно любого актива возможна «короткая продажа»; налоги и издержки, связанные с покупкой и продажей активов, не принимаются во внимание.

Пусть инвестор формирует свой портфель сроком на один период владения из N рисковых ценных бумаг. Ожидаемая доходность и ковариационная матрица доходностей активов для рассматриваемого периода равны 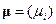 и S. Будем полагать, что ковариационная матрица S является невырожденной и приемлемая доходность портфеля ценных бумаг равна .

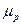Задача заключается в определении такой структуры портфеля (вектор x), которая обеспечила достижения заданной доходности портфеля 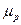 с минимальным риском. Математическая формулировка задачи имеет вид:

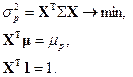
Данная задача известна как задача Марковитца.

Вектор x являющийся решением задачи Марковитца, определяет структуру оптимального портфеля среди всех возможных портфелей с ожидаемой доходностью 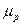. В рассматриваемом случае компоненты вектора x могут принимать отрицательные значения, что означает рекомендацию инвестора совершить относительно соответствующих активов операцию “короткая продажа”.

В математическом плане задача Марковитца может быть решена с помощью метода неопределенных множителей Лагранжа.

Портфели, оптимальные в смысле задачи Марковитца, называются эффективными портфелями рисковых ценных бумаг.

Свойства эффективных портфелей:

1. С увеличением ожидаемой доходности портфеля вклады x_i в ценные бумаги при возможности операции «короткая продажа» изменяются линейно: увеличиваются для более доходных и уменьшаются для менее доходных активов.

2. Риск оптимального портфеля возрастает вместе с ростом ожидаемой доходности. При возможности операции «короткая продажа» возможно достижение сколь угодно высокой доходности при соответственно растущем риске.

3.  Эффективные портфели имеют максимальную доходность среди всех достижимых портфелей с одинаковым риском и имеют минимальный риск среди всех достижимых портфелей с одинаковой доходностью.

Множеству всех эффективных портфелей соответствует отрезок кривой от точки G (включая глобальный портфель G) до точки А и выше (рис. 9). Портфели, лежащие на отрезке кривой от точки G до точки В и ниже являются неэффективными. Портфели, лежащие в заштрихованной области, ограниченной кривой (включая и саму кривую), образуют множество допустимых портфелей.

Таким образом, в результате решения задачи Марковица инвестор получает бесконечное множество эффективных портфелей. Индивидуальные предпочтения инвестора учитываются с помощью кривых безразличия данного инвестора (рис. 10).

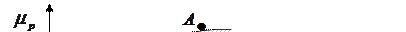
Рис. 9. Фронт эффективных портфелей:

А,С – эффективные портфели; G – «глобальный» эффективный портфель;

 В – неэффективный портфель

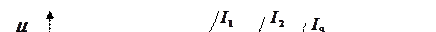
Рис. 10. Выбор оптимального портфеля с учетом предпочтений инвестора, задаваемых кривыми безразличия

Пусть портфели, соответствующие различным уровням притязаний инвестора, описываются кривыми безразличия I ₁, I ₂, I ₃.

Фронту эффективных портфелей соответствует отрезок G - A. Портфели, принадлежащие кривой безразличия I ₁ являются недостижимыми. Среди достижимых и приемлемых портфелей эффективными являются портфели А, С, D. Оптимальным и более эффективными из них являются портфель С, так как лежит на кривой безразличия I ₂, что выше и левее кривой I ₃.

6