Необходимые для расчета продолжительности ссуды в годах и днях формулы получим из формул (1.1) и (1.4) относительно n.
Срок в годах:
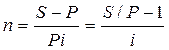 ,
,
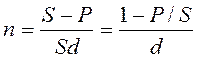 .
.
Срок в днях, учитывая, что n = t /К, где К — временная база):
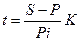 , (1.5)
, (1.5)
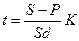 .
.
Для определения финансовой эффективности операции и при сравнении контрактов по их доходности в случаях, когда процентные ставки в явном виде не указаны, применяем следующие формулы для сроков, измеренных в годах и днях:
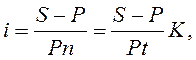 (1.6)
(1.6)
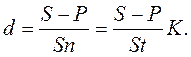 (1.7)
(1.7)
Наращение процентов в потребительском кредите
В потребительском кредите проценты, как правило, начисляются на всю сумму кредита и присоединяются к основному долгу уже в момент открытия кредита.
Погашение долга с процентами производится частями, обычно равными суммами на протяжении всего срока кредита.
Таким образом, наращенная сумма на весь срок равна
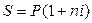 ,
,
величина разового погасительного платежа составит
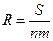 , (1.8)
, (1.8)
где n — срок кредита в годах, m — число платежей в году.
В связи с тем, что проценты здесь начисляются на первоначальную сумму долга, а его фактическая величина систематически уменьшается во времени, действительная стоимость кредита заметно превышает договорную процентную ставку.
Замена платежей
На практике возникают случаи, когда необходимо заменить одно денежное обязательство другим, например, с более отдаленным сроком платежа, объединить несколько платежей в один (консолидировать платежи) и т.п. Возникает вопрос о финансовой эквивалентности обязательств.
Эквивалентными считаются такие платежи, которые, будучи приведенными к одному моменту времени, оказываются равными. То есть две суммы S1 и S2, выплачиваемые в разные моменты времени, считаются эквивалентными, если их современные (или наращенные) величины, рассчитанные по одной и той же процентной ставке и на один момент времени, одинаковы.
Допустим, сравниваются два платежа S1 и S2 со сроками n1 и n2 , причем S1 < S2 и n1<n2. С ростом i размеры современных стоимостей Р1, Р2 уменьшаются. На основе равенства
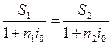
находим
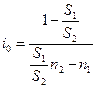 .
.
При ставке i = i0 наблюдается равенство Р1 = Р2. Назовем ставку i0 , при которой достигается равенство первоначальных сумм, критической или барьерной.
Одним из распространенных случаев изменения условий контрактов является консолидация (объединение) платежей. Пусть платежи S1, S2, …, S m со сроками n1, n2, …n m заменяются одним S0 и сроком n0.
При применении простых процентных ставок сумму консолидированного платежа можно найти по формулам:
§ 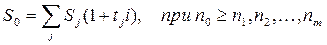 , где
, где 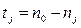 ;
;
§ 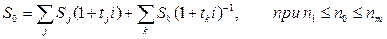 ,
,
где 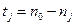 ,
, 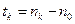 ,
,
Sj – сумма объединяемых платежей со сроком nj ( 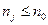 ),
),
Sk – сумма объединяемых платежей со сроком nk ( 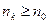 ).
).
Контур финансовой операции
Пусть выдана ссуда на срок T размере Р. На протяжении этого срока в счет погашения задолженности производятся, допустим, два платежа R1 и R2, а в конце срока выплачивается остаток задолженности в сумме R3 На интервале t1 задолженность возрастает, в силу начисления процентов, до величины P1 . В конце этого периода выплачивается в счет погашения задолженности сумма R1. Долг уменьшается до K1 и т.д. Заканчивается операция получением кредитором в окончательный расчет суммы R3. В этот момент задолженность должна быть равна нулю. Такой график называется контуром операции.
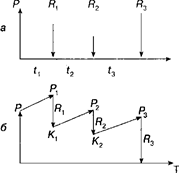
Рис. 2. Контур операции
Сбалансированная операция, при которой последняя выплата полностью покрывает остаток задолженности, обязательно имеет замкнутый контур (рис. 2).
Сложные проценты
Дата: 2019-03-05, просмотров: 370.