Пусть 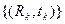 - инвестиционный процесс – поток платежей R_k в момент t_k, знак R_k - если положителен – это доход, отрицательный – затраты или инвестиции. Все платежи производятся на стыке лет и только в неотрицательные номера лет. Процесс называется конечным, если в нем имеется последний платеж, иначе – бесконечным.

Приведенным чистым доходомNPV (Net Present Value) называется сумма всех платежей, дисконтированных к моменту 0 по действующей ставке i:

.

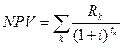Процесс называется окупающимся, если NPV > 0.

Для конечного процесса можно определить наращенный чистый доходNFV (Net Future Value) –это алгебраическая сумма всех платежей, дисконтированных к моменту t_k последнего платежа по ставке процента i:

.

.

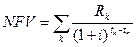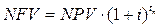Далее будем рассматривать только процессы, у которых существуют инвестиции в момент 0, а все остальные платежи положительны, т.е. это доходы. Для таких процессов интересной характеристикой является внутренняя доходность процесса q – такое наименьшее положительное число, что алгебраическая сумма всех платежей, дисконтированных к моменту 0 по ставке q равна 0, т.е. 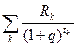=0.

Если процесс окупающийся, то .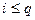

Внутренняя норма доходности показывает предельный уровень ставки процента, при котором взятые по этой ставке инвестиции окупаются доходами процесса, наращиваемые по той же ставке:

.

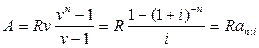Пусть имеется проект, на который следует инвестировать некоторую сумму, затем он будет приносить доход в течение n лет. То есть имеем поток доходов, представляющих собой конечную годовую ренту с годовым платежом R, длительностью n лет. Современная величина этой ренты:

,

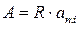где 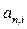- коэффициент приведения ренты.

Приведенный чистый доход есть

.

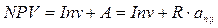Доходность проекта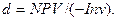

Пусть s – срок окупаемости, то s должно быть минимальным из всех таких чисел r, что NPV³0, т.е.

,

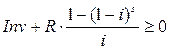тогда

.

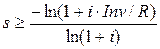Внутренняя доходность проекта q должна удовлетворять уравнению

,

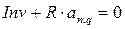где 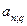- коэффициент приведения ренты. Решая это уравнение, находим q.

Бесконечный проект можно рассматривать как вечную ренту. Для вечной ренты современная величина вычисляется по формуле:

.

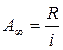Если разрабатывается инвестиционный проект заданной длительности, с которой совпадает срок окупаемости (NPV=0). В этом случае, так как срок окупаемости равен сроку проекта, то 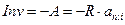, современная и наращенная величины дохода проекта равны 0. Доходность проекта также равна 0, а внутренняя доходность совпадает со ставкой процента q = i.

Пусть инвестиции заданы одной суммой и имеется постоянный поток доходов. Тогда из условия полной окупаемости за срок n _ок при заданной процентной ставке i и ежегодных поступлений R следует:

.

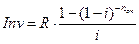Отсюда

.

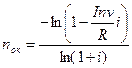Если необходимо обеспечить большую доходность j вложения инвестиций, чем просто общепринятая ставка процента i ,  то ежегодный доход должен удовлетворять уравнению 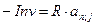, или 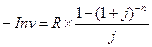. Минимальный ежегодный доход равен:

.

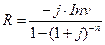Рассмотрим процесс со следующими параметрами: Inv, R, n.

Коэффициент приведения ренты:

.

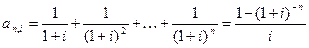Видно, что при увеличении i 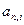, уменьшается. Поэтому при увеличении ставки процента приведенный чистый доход  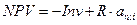уменьшается, следовательно, уменьшается доходность процесса, а срок окупаемости увеличивается. Внутренняя доходность процесса не зависит от ставки процента, так как определяется исключительно размером инвестиций и потоком доходов. Таким образом, вполне может быть так, что инвестиционный проект окупается при одной ставке и не окупается при большей ставке.

Часто приходится сравнивать инвестиционные проекты, различающиеся по затратам, но тождественные по результатам. Естественно, в такой ситуации оценивать проекты надо по их затратам, причем наряду с капитальными затратами К, осуществляемыми на начальный стадии проекта, надо учитывать и текущие издержки С (на ремонт, обновление и т.п.), различные по годам, но для упрощения предположим их одинаковыми.

Сравниваем проекты путем подсчета современной величины А _m потока затрат по m-му проекту. Довольно естественным считать этот поток затрат бесконечным и потому

,

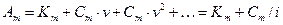где v = 1/(1 + i) – дисконтирующий множитель по ставке сравнения i.

Из сравниваемых проектов лучшим надо считать тот проект m, у которого современная величина потока затрат K_m + C_m/i наименьшая, что эквивалентно тому, что наименьшей является величина С _m + iK_m. Это выражение называется показателем приведенных затрат.

Своеобразным инвестиционным процессом является аренда оборудования. Для владельца оборудования важно обеспечить нужный уровень эффективности сдачи в аренду, для арендатора: купить оборудование или его арендоватьДля этого необходимо определить размер арендных платежей.

Пусть оборудование стоимостью Р сдается в аренду на n лет. К концу этого срока остаточная его стоимость составит S. Таким образом, владелец оборудования «теряет» P – S/(1 + j)ⁿ, где (1 + j) – коэффициент дисконтирования, приведения суммы S к началу аренды, к расчетному моменту. Величина j может быть отождествлена с доходностью сдачи оборудования в аренду для владельца оборудования. «Потерю» владельцу должен возместить арендатор. Современная величина потока его арендных платежей по ставке j должна быть равна 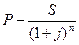, так что размер разового годового арендного платежа R может быть определен из уравнения

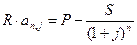.                                (4.1)

Следовательно, этот годовой платеж .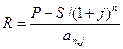

Ясно, что норматив доходности j должен быть больше нормы амортизации h. Разность j – h в некоторой мере характеризует эффективность сделки.

В формуле (4.1) 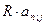 - современная величина арендных платежей при ставке процента i, а  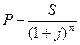- современная величина потерь, связанных с покупкой. Поэтому, если выполняется условие

,

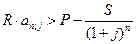то для владельца выгоднее сдать в аренду, а для арендатора – купить.