Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

 

Для оценки тесноты связи количественных показателей (измеряемых числами) могут использоваться несколько различных характеристик.

Основные из них следующие.

1. Линейный коэффициент корреляции 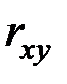 выражает степень тесноты линейной связи между двумя количественными переменными X и Y (нормированный корреляционный момент взаимосвязи переменных).

По выборочным данным линейный коэффициент корреляции вычисляется по следующим формулам:

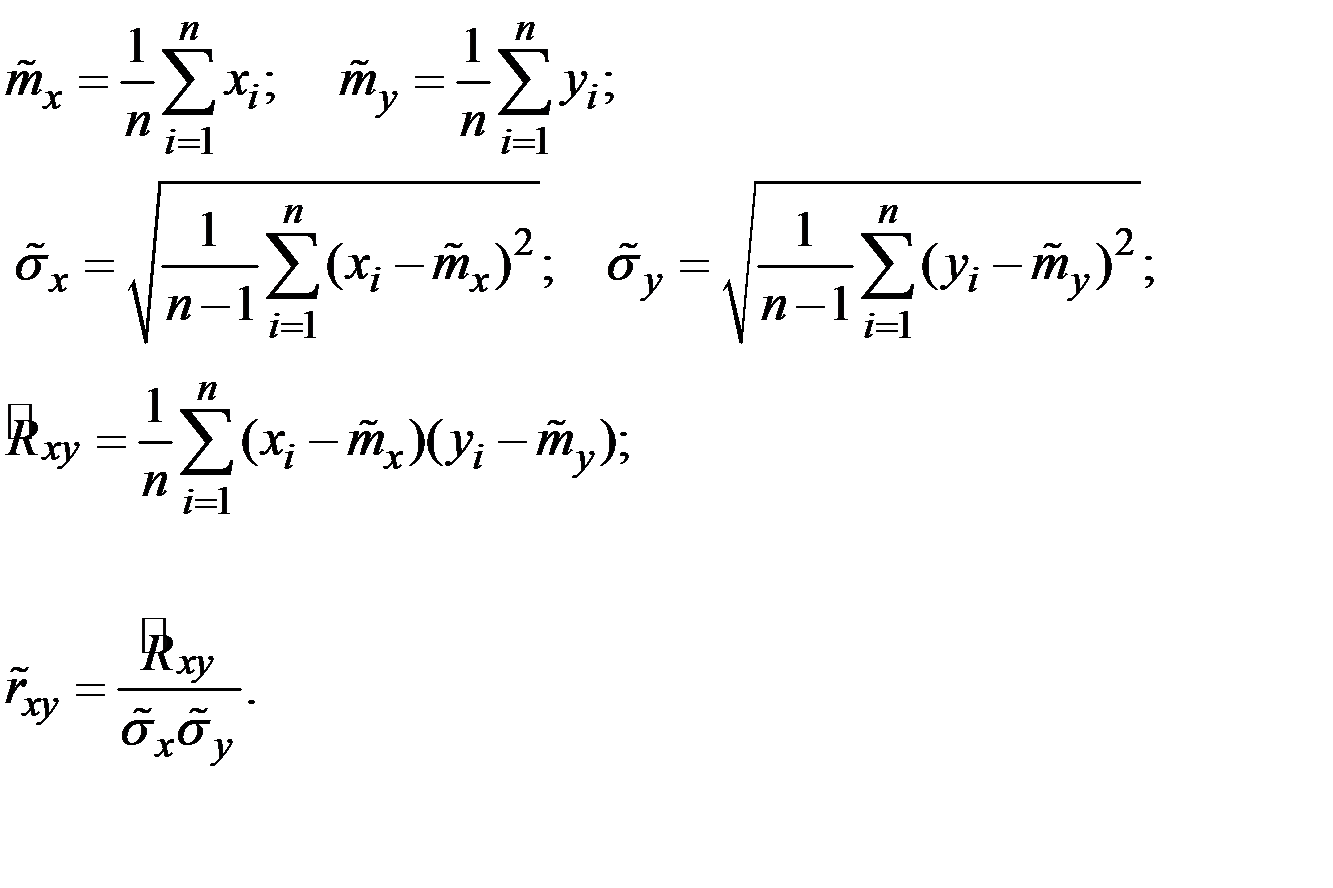
Основные свойства коэффициента корреляции:

r_xy = r_{y х} = r(X,Y) = r(aX + b , cY + d); (а > 0; c > 0).

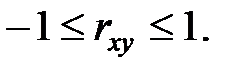
Коэффициент корреляции (по модулю) не изменяется при линейных преобразованиях переменных.

Если имеем уравнения регрессии в виде ; 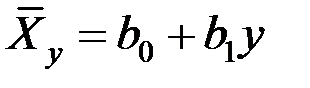, то коэффициент корреляции выражается через коэффициенты регрессии по соотношению: .

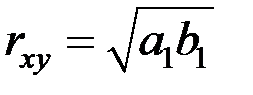Проверка гипотезы о значимости выборочного парного линейного коэффициента корреляции ( 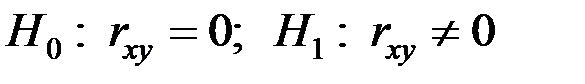) осуществляется с использованием Т–критерия Стъюдента

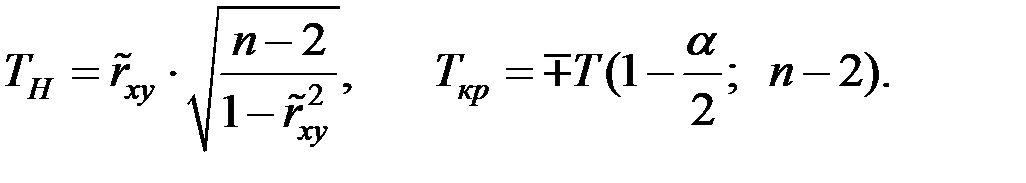
2. Эмпирическое (статистическое) корреляционное отношение 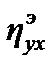 применяется для оценки тесноты нелинейной связи между переменными, представленными в виде сгруппированных статистических данных.

Обычно исходные данные могут быть собраны в следующую таблицу значений системы двух случайных величин (Х,Y):

			...		...
			...		...
			...		...
...	...	...	...	...	...	...
			...		...
...	...	...	...	...	...	...
			...		...

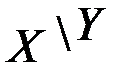
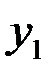
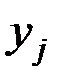
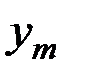
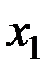
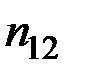
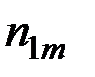
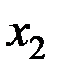
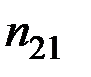
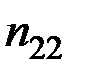
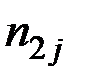
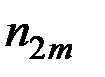
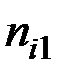
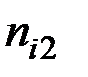
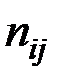
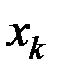
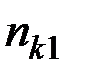
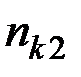
Здесь 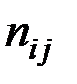– количество вариантов, давших сочетание рассматриваемых величин (X = х_i, Y = у_j).

При этом .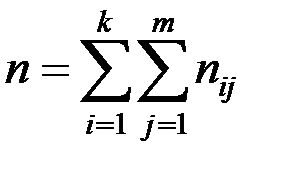

По данной таблице можно вычислить следующие параметры:

1) средние значения величин X и Y:

,            

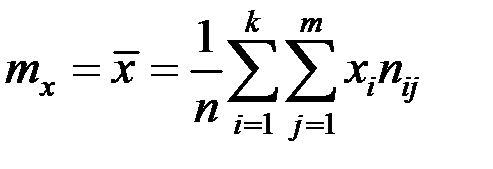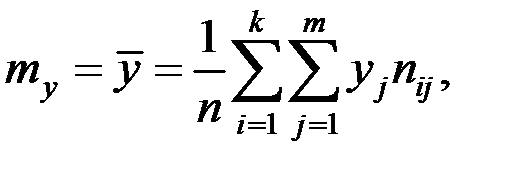
2) дисперсии величин X и Y:

           

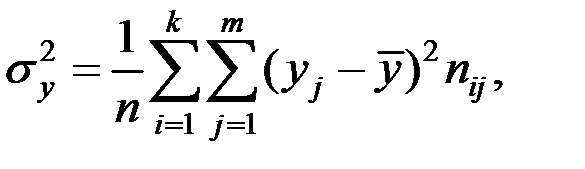
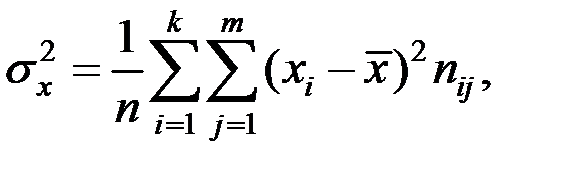
3) средние значения Y при фиксированном 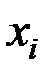, т.е. средние по строкам (межгрупповые средние):           

;

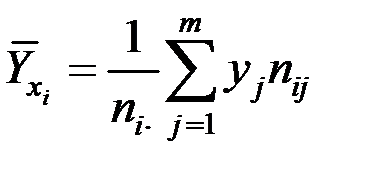4) средние значения X при фиксированных :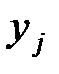 

.

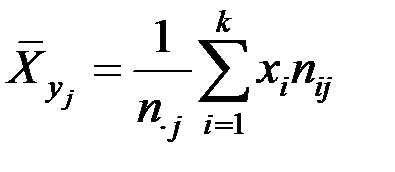Здесь использованы следующие обозначения:

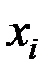 – такое число раз встречалось значение ;

 – такое число раз встречалось значение .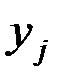

По таблице данных можно также вычислить:

– межгрупповую (факторную) дисперсию

;

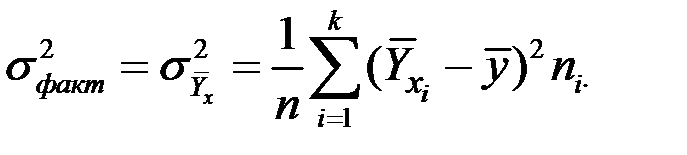– остаточную дисперсию 

;

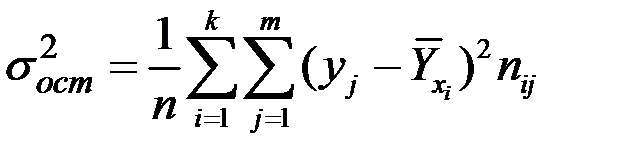– общую дисперсию

.

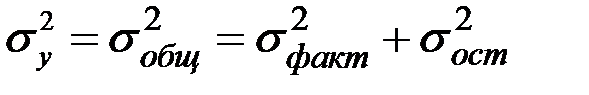Тогда статистическое корреляционное отношение вычисляется по формуле

.

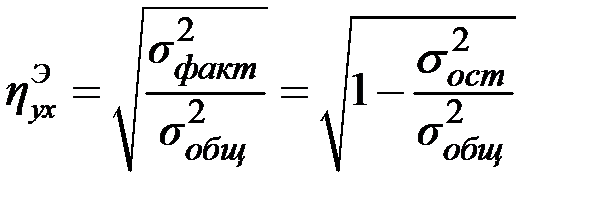Корреляционное отношение показывает, какую часть общей изменчивости составляет межгрупповая изменчивость.

Свойства :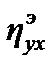

1) 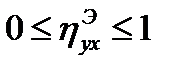; при этом  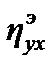= 1 для функциональной связи,  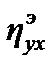= 0 для независимых величин Х и Y;

2) 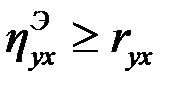; равенство  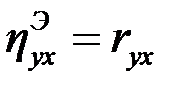справедливо, если связь между величинами Х и Y линейная.

Степень расхождения 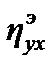 и  может служить F–критерием для принятия гипотезы о линейности связи между переменными Х и Y (пример 4.1):

; ,

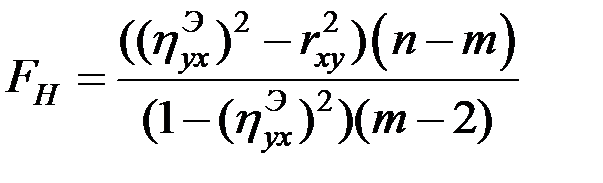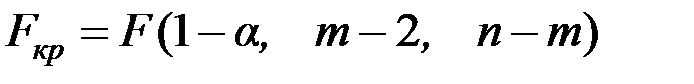где n – число наблюдений (опытов);

m – число сгруппированных интервалов для показателя Y.

Проверка значимости статистического корреляционного отношения 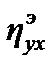 ( 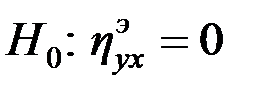) осуществляется по критерию

.

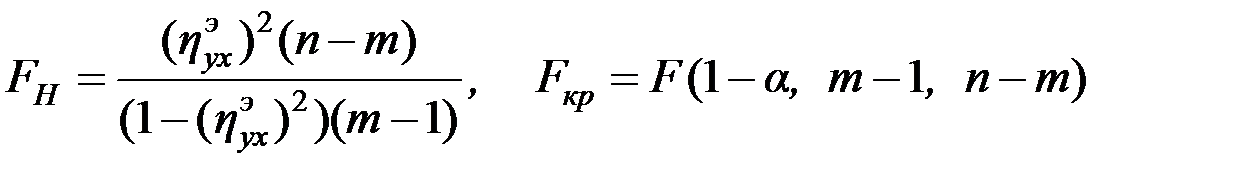3. Теоретическое корреляционное отношение (индекс корреляции) 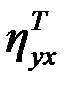 (или просто ).

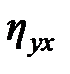Формулы расчёта 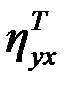 аналогичны формулам для  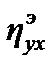за исключением того, что используются не групповые средние , а значения функции регрессии (х_i), т.е. значения величины Y, вычисленные по некоторой кривой (функции) связи Y и Х при значении х_i.

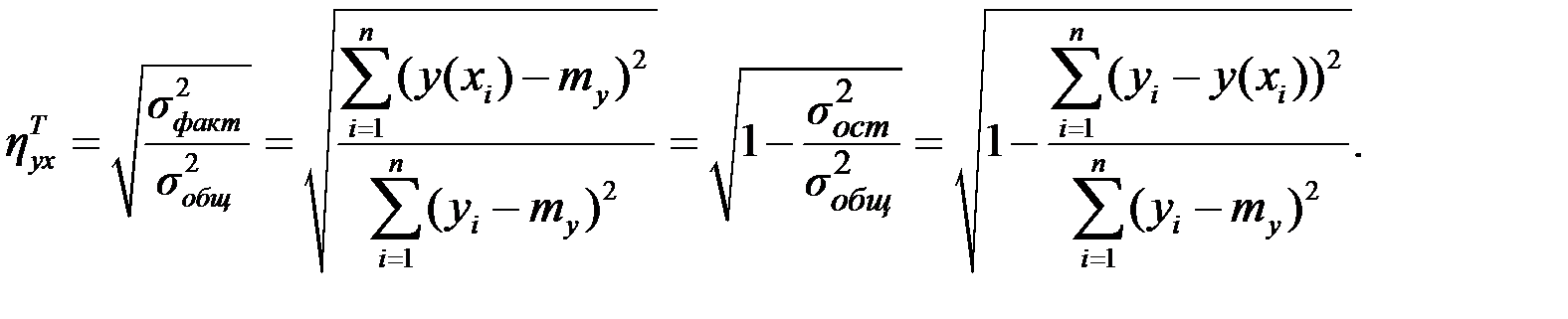
Фактически, 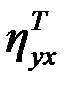 оценивает степень близости кривой регрессии к имеющимся данным, т.е. степень удачности выполнения регрессионного анализа.

Для 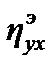 и 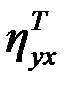 имеет место неравенство

.

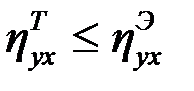Оно справедливо за счёт того, что кривая регрессии не всегда проходит через групповые средние.

Проверка значимости индекса корреляции (теоретического корреляционного отношения 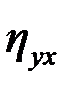) ( ) приводит к критерию

4. Коэффициент множественной корреляции характеризует тесноту линейной связи между одним зависимым и несколькими независимыми показателями.

Если имеются m показателей 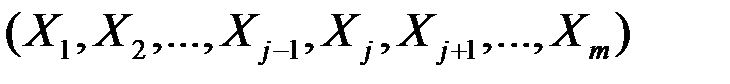, то выборочный коэффициент множественной корреляции показателя  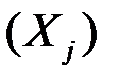характеризует тесноту линейной связи между этим зависимым и остальными независимыми показателями  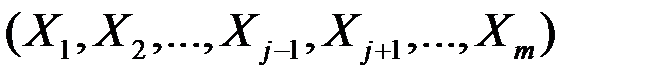и вычисляется по формуле  

.

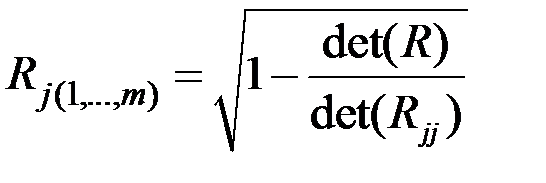Здесь 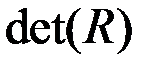 – определитель корреляционной матрицы

;

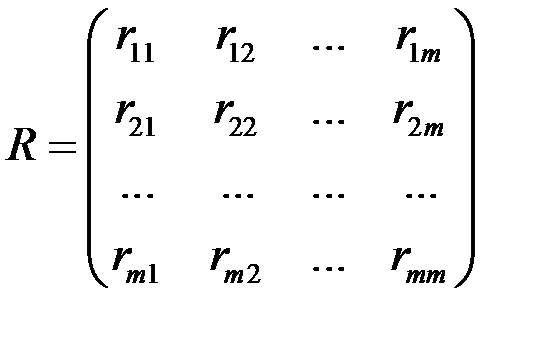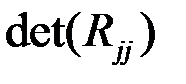 – определитель матрицы алгебраических дополнений элемента  матрицы R. 

Напомним, что алгебраическим дополнением 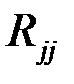 элемента  матрицы R называется матрица

,

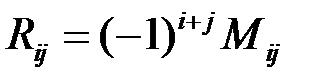где 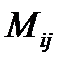 – минор элемента , т.е. определитель порядка 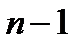, полученный из исходного вычёркиванием i –й строки и j –го столбца матрицы R.

В случае зависимости результирующей величины от двух переменных 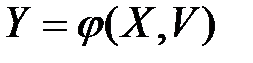 коэффициент множественной корреляции вычисляется по формуле

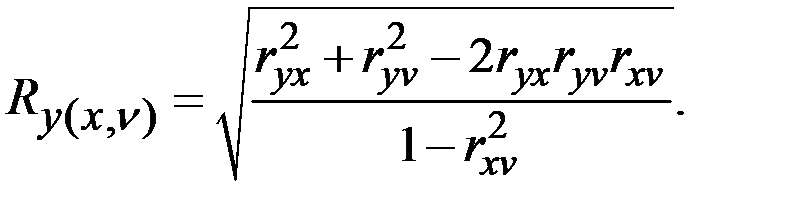
5. Частные (парциальные) коэффициенты корреляции используются для оценки тесноты связи между двумя показателями из нескольких при элиминированном (исключённом) влиянии других показателей.

Если имеются m показателей 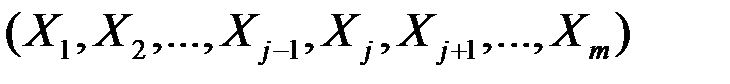, то частный коэффициент корреляции показателей  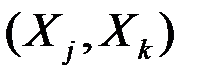вычисляется по формуле                                

.

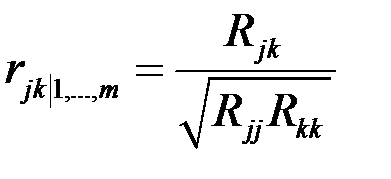Пусть мы имеем три показателя X, Y, V.

Частный коэффициент корреляции между X и Y при исключении V определяется через парные коэффициенты корреляции соотношением:

.

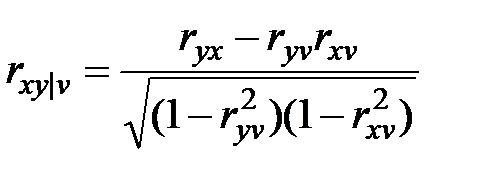Абсолютные величины частных коэффициентов корреляции не могут быть больше величины коэффициента множественной корреляции.

6. Коэффициент детерминации 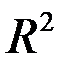 есть квадрат коэффициента корреляции (для линейной связи) или квадрат корреляционного отношения (для нелинейной зависимости) величин Х и Y или квадрат коэффициента множественной корреляции: 

, , .

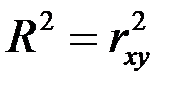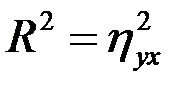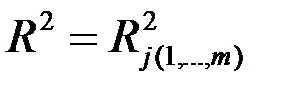Пример 4.1. По 50 наблюдениям оценили тесноту связи двух экономических показателей с помощью статистического корреляционного отношения и линейного коэффициента корреляции.

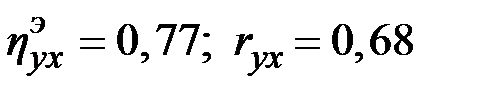Получили следующие оценки параметров (при группировке показателя  на 5 интервалов): . Какую форму регрессионной зависимости следует искать: линейную или нелинейную?

Решение. Проверим гипотезу о линейности связи между переменными (проверяемая гипотеза: различие между статистическим корреляционным отношением и линейным коэффициентом корреляции незначимо).

Тогда по критерию Фишера получаем

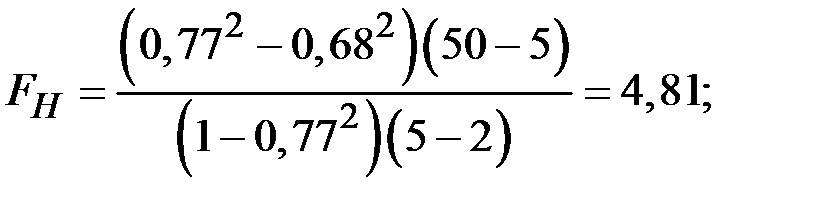
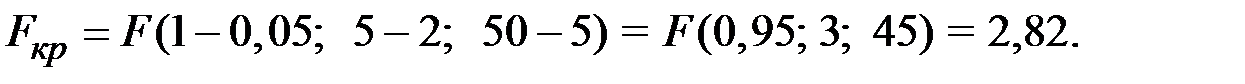
Вывод: целесообразно использовать нелинейную регрессию.

Пример 4.2. Исследовалась взаимосвязь между тремя показателями: производительностью труда ( 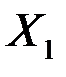), возрастом ( 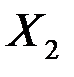), и производственным стажем ( 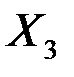). По выборке из 100 рабочих одной и той же специальности вычислены парные коэффициенты корреляции: 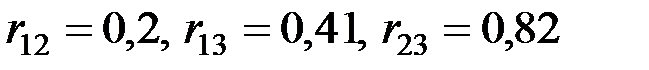. Вычислить множественные и частные (парциальные) коэффициенты корреляции. Оценить значимость этих коэффициентов.

Решение. Вычислим множественные коэффициенты корреляции, характеризующие связь между одним зависимым и двумя независимыми показателями.

;

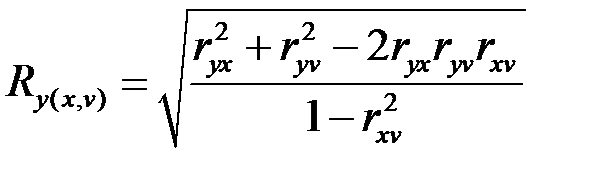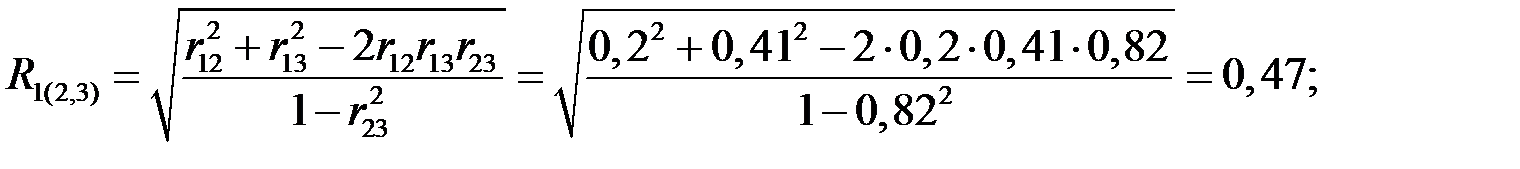
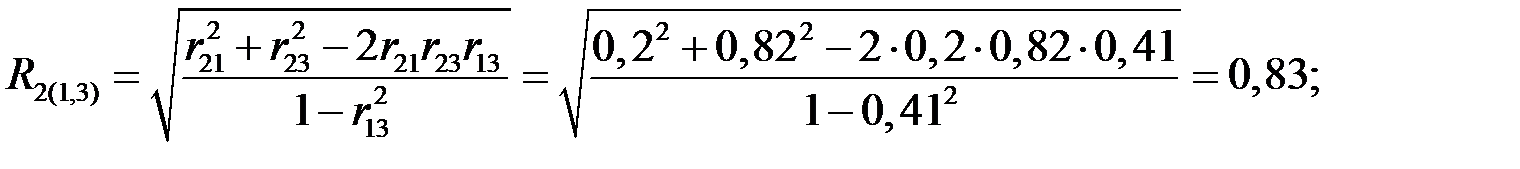
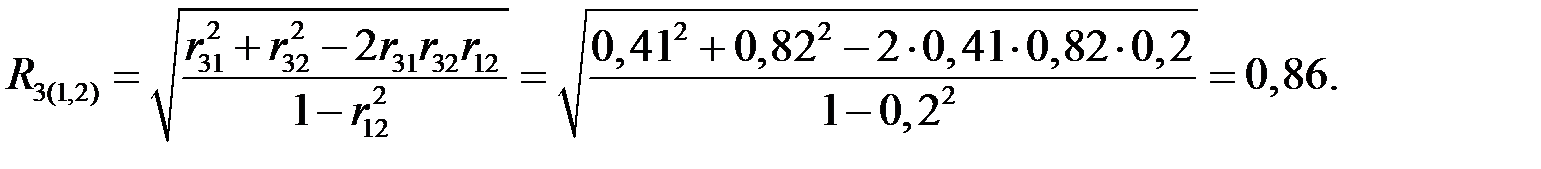
Оценим значимость вычисленных множественных коэффициентов корреляции при уровне значимости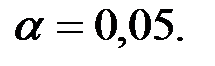

Проверка гипотезы о значимости множественного коэффициента корреляции ( ) осуществляется с использованием 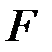– критерия. Вычислим наблюдаемое значение критерия:

,

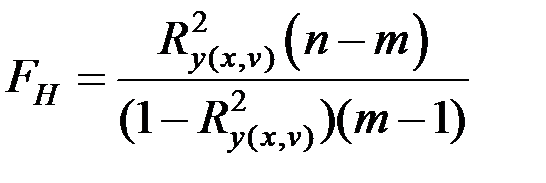где 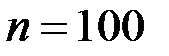 – объём выборки,  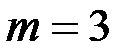– количество показателей.

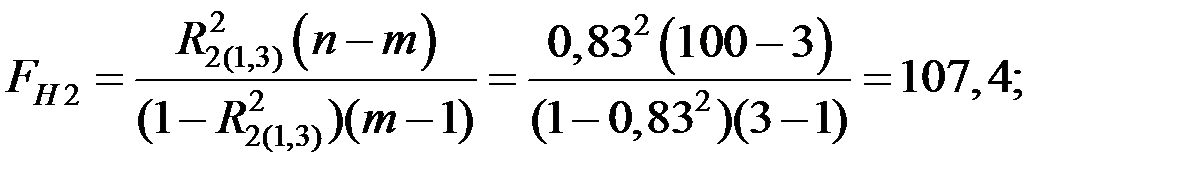
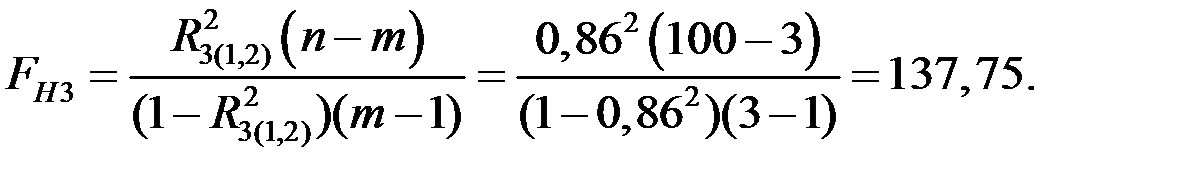
По таблице квантилей 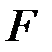– распределения найдём критическую точку.

        

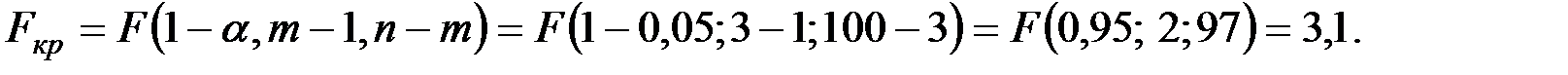
Так как все 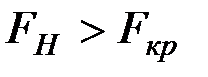, то гипотезу  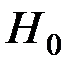отвергаем, т.е. множественные коэффициенты корреляции значимы.

Вычислим частные (парциальные) коэффициенты корреляции, характеризующие связь между двумя показателями при исключённом влиянии третьего.

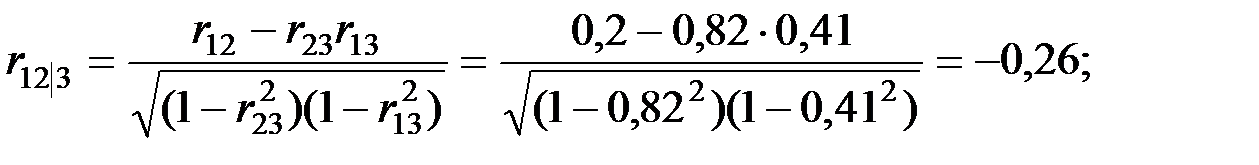
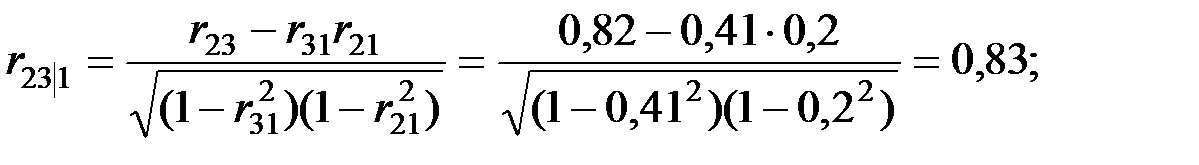
Обратим внимание на то, что парный и частный коэффициенты корреляции между производительностью труда и возрастом имеют разные знаки. Это объясняется существенным влиянием стажа работы на производительность.

Оценим значимость вычисленных частных (парциальных) коэффициентов корреляции при уровне значимости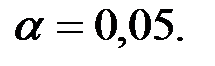

Проверка гипотезы о значимости частного коэффициента корреляции ( 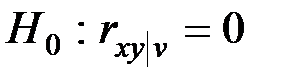) осуществляется с использованием 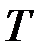−распределения Стьюдента.

Вычислим наблюдаемое значение критерия: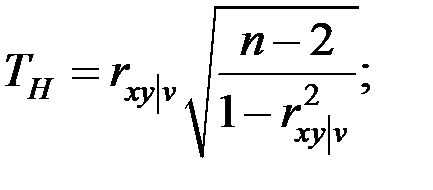

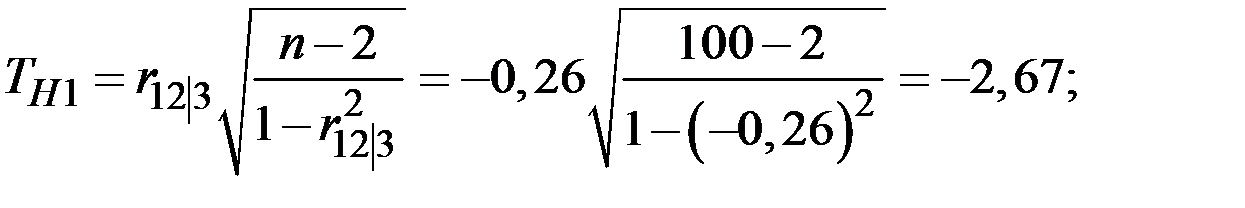
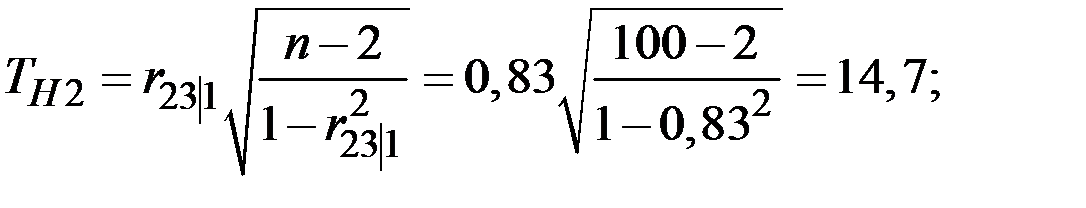
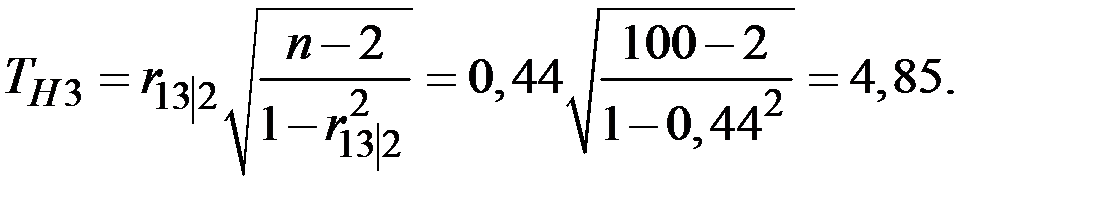
По таблице квантилей 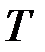 − распределения Стьюдента найдём критическую точку.

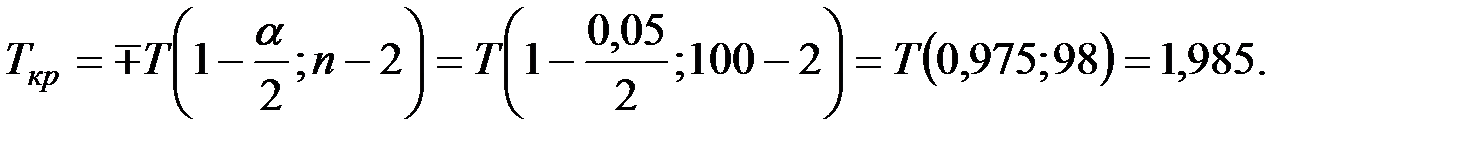
Так как все 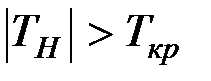, то гипотезу  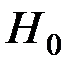отвергаем, т.е. частные (парциальные) коэффициенты корреляции значимы.

Пример 4.3. По 30 различным предприятиям области собраны статистические данные за прошедший год о доле (проценте) прибыли, направленной для выплаты дивидендов по своим акциям, и объёме средств (млн. руб.), выделенных на развитие производства (табл. 4.1).

Таблица 4.1

Показатели статей расхода средств предприятий области

№ предприятия	Прибыль для выплаты дивидендов по акциям, %	Объём средств, направленных на развитие производства, млн. руб.
1	11,9	17,6
2	16,3	11,4
3	9,1	33,4
4	11,4	29,6
5	13,4	15,5
6	21,7	10,0
7	18,3	19,3
8	15,5	6,0
9	16,8	28,3
10	12,0	21,5
11	19,3	11,7
12	13,6	23,5
13	15,0	17,7
14	14,0	27,0
15	17,1	14,9
16	8,7	25,5
17	16,6	17,4
18	15,3	24,6
19	16,2	20,4
20	18,6	9,5
21	15,7	28,1
22	14,4	24,0
23	16,0	27,4
24	18,2	12,0
25	17,2	29,6
26	10,8	36,0
27	18,0	13,1
28	11,5	31,8
29	9,7	35,5
30	20,4	10,7

 

Необходимо:

1) получить интервальный ряд, характеризующий распределение предприятий по сумме средств, направленных на развитие производства, образовав пять групп с равными интервалами;

2) построить корреляционную таблицу и аналитическую группировку для изучения связи между процентом прибыли для выплаты дивидендов по акциям и объёмом средств, направленных на развитие производства;

3) найти корреляционное отношение и коэффициент корреляции между изучаемыми показателями и сделать выводы.

Решение. Для изучения структуры предприятия по объёму средств, направленных на развитие производства, пользуясь данными табл. 4.1, построим интервальный вариационный ряд, характеризующий распределение предприятий по объёму затраченных средств.

Величина интервала равна

h = (х_max – x_min) / m,

где x_min  и x_max – минимальное и максимальное значения изучаемой величины; m – необходимое колличество интервалов.

Получаем:  h = (36 – 6) / 5 = 6,0 млн. руб.

Путём прибавления величины интервала к минимальному уровню признака в группе получим следующие группы предприятий по объёму затраченных средств на развитие производства (табл. 4.2).

Таблица 4.2

Распределение предприятий по объёму средств на развитие производства

Номер группы	Объём средств на развитие производства, млн. руб.	Число предприятий
		в абсолютном выражении	в относительных единицах, %
I	6 – 12	7	23,3
II	12 – 18	6	20,0
III	18 – 24	5	16,7
IV	24 – 30	8	26,7
V	30 – 36	4	13,3
Итого		30	100,0

Данные группировки показывают, что 56,7% предприятий затрачивают на развитие производства свыше 18 млн. руб.

Определим, существует ли зависимость между прибылью для выплаты дивидендов (факторный признак X) и размером затраченных средств (результативный признак Y).

Для этого построим корреляционную таблицу, образовав пять групп по факторному и результативному признакам (табл. 4.3).

Для построения данной таблицы необходимо разбить прибыль для выплаты дивидендов по акциям на четыре интервала с определённым шагом (в данном случае h = 3,25%).

Таблица 4.3

Распределение предприятий по прибыли для выплаты дивидендов

и объёмом средств на развитие предприятия

Прибыль для выплаты дивидендов по акциям, %	Объём средств на развитие производства, млн. руб.
	6 – 12	12 – 18	18 – 24	24 – 30	30 – 36
8,7 – 11,95		1		2	4
11,95 – 15,2		2	3	1
15,2 – 18,45	3	3	2	5
18,45 – 21,7	4

 

Из данных табл. 4.3 видно, что распределение числа предприятий произошло вдоль диагонали, проведённой из левого нижнего угла в правый верхний угол таблицы. Уменьшение признака «прибыль для выплаты дивидендов по акциям» сопровождалось увеличением признака «объём затраченных средств на развитие производства».

Характер концентрации частот по диагонали корреляционной таблицы свидетельствует о наличии обратной, достаточно тесной корреляционной связи между изучаемыми признаками.

Установим наличие и характер связи между прибылью для выплаты дивидендов по акциям и объёмом затраченных средств на развитие предприятия методом аналитической группировки (табл. 4.4).

Для того чтобы расчитать среднюю прибыль для выплат в группе необходимо сложить все значения прибыли по каждому предприятию группы и поделить на количество предприятий в группе. По тому же принципу определяется средняя прибыль данной выборки в целом и средний объём затраченных средств на одно предприятие.

Например, для первой группы средняя прибыль для выплаты:

(11,9 + 9,1 + 11,4 + 8,7 + 10,8 + 11,5 + 9,7) / 7 = 10,4 млн. руб.

Объём средств всего:

17,6 + 33,4 + 29,6 + 25,5 + 36 + 31,8 + 35,5 = 209,4 млн. руб.

В среднем на одно предприятие первой группы затрачивается

209,4 / 7 = 29,9 млн. руб.

Данные табл. 4.4 показывают, что с ростом прибыли для выплаты дивидендов по акциям, объём средств затрачиваемых на развитие производства, уменьшается. Следовательно, между исследуемыми признаками существует обратная корреляционная зависимость.

Таблица 4.4

Зависимость объёма затраченных средств на развитие производства от прибыли для выплаты дивидендов по акциям

 

№ п/п	Прибыль для выплаты дивидендов по акциям, %	Число предприятий в группе	Средняя прибыль для выплат в группе	Объём затраченных средств, млн. руб.
				всего	в среднем на одно предприятие
I	8,7 – 11,95	7	10,4	209,4	29,9
II	11,95 – 15,2	6	13,7	129,2	21,5
III	15,2 – 18,45	13	16,7	252,5	19,4
IV	18,45 – 21,7	4	20,0	41,9	10,5
Итого		30	15,1	633,0	21,1

 

По данным таблицы 4.4 определим корреляционное отношение.

Для этого необходимо найти среднее значение Y при фиксированном х _i, т.е. средние по строкам:   

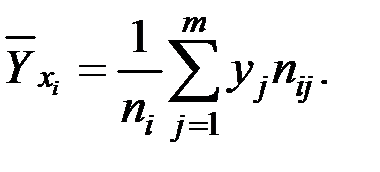
Получим:

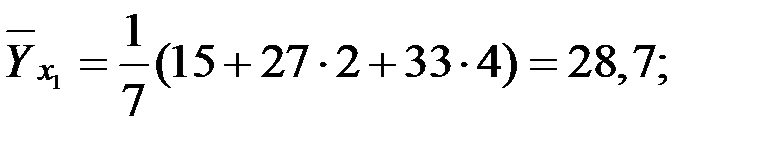
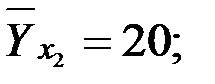
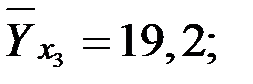
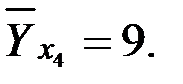
Определим межгрупповую (факторную) и остаточную дисперсию для определения общей дисперсии.

   

  

  

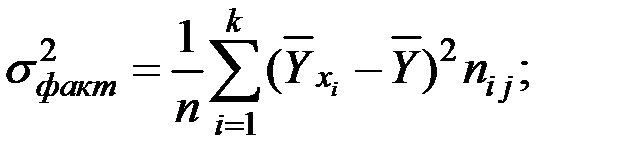
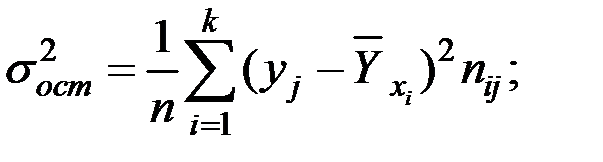
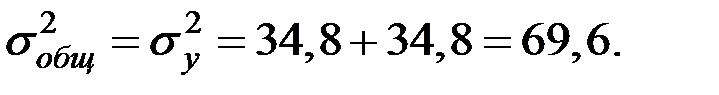
Рассчитаем эмпирическое корреляционное отношение

 

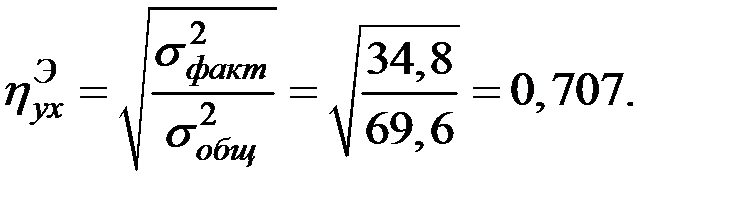
Вычислим величины ,  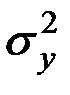и 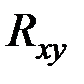 по формулам:

 

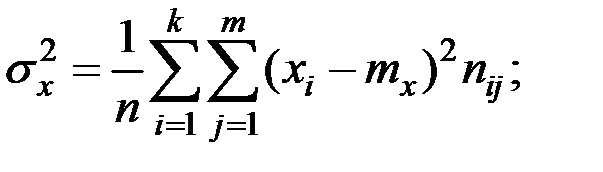
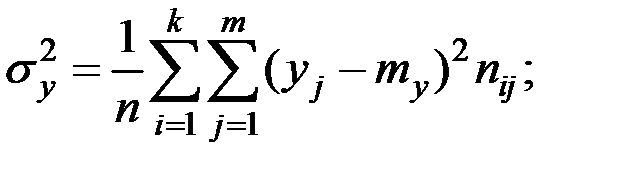
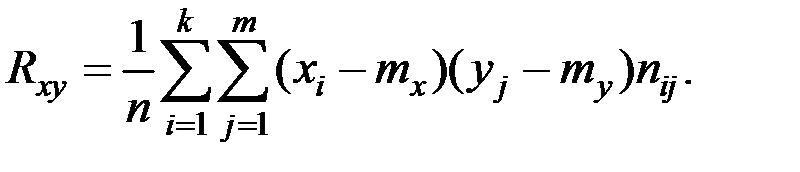
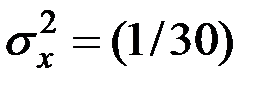 [7 (10,4 – 15,1)² + 6 (13,7 – 15,1)² + 13 (16,7 – 15,1)² +

+ 4 (20,0 – 15,1)²] = 10,4;

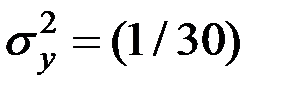 [7 (29,9 – 21,1)² + 6 (21,5 – 21,1)² + 13 (19,4 – 21,1)² +

+ 4 (10,5 – 21,1)²] = 69,6;

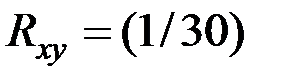 [(10,325 – 15,1) (15 – 21,1) + 2 (10,325 – 15,1) (27 – 21,1) +

+ 4 (10,325 – 15,1) (33 – 21,1) + 2 (13,575 – 15,1) (15 – 21,1) +

+ 3 (13,575 – 15,1) (21 – 21,1) + (13,575 – 15,1) (27 – 21,1) +

+ 3 (16,825 – 15,1) (9 – 21,1) + 3 (16,825 – 15,1) (15 – 21,1) +

+ 2 (16,825 – 15,1) (21 – 21,1) + 5 (16,825 – 15,1) (27 – 21,1) +

+ 4 (20,075 – 15,1) (9 – 21,1)] = – 17,7.

Рассчитаем среднеквадратическое отклонение величин X и Y:

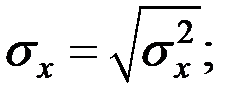
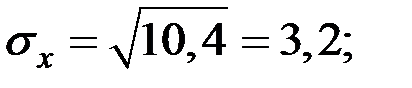
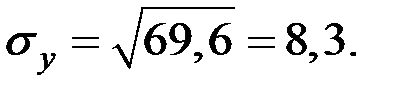
Определяем коэффициент корреляции по формуле

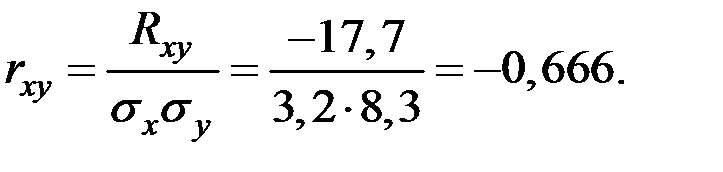
По полученным данным можно сделать вывод, что зависимость между величинами X и Y скорей всего линейная, а корреляционная связь довольно тесная и обратная, так как коэффициент корреляции отрицателен, т.е. при снижении прибыли для выплаты дивидендов, сумма средств затраченных на развитие предприятия возрастает.