Значения yi, соответствующие данным х i при теоретических значениях а и b модели парной регрессии 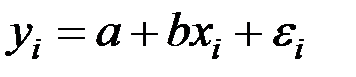 являются случайными.
являются случайными.
Случайными являются и рассчитанные по ним значения коэффициентов а и b. Надёжность получаемых оценок а и b зависит от дисперсии случайных отклонений (ошибок).
По данным выборки эти отклонения и соответственно их дисперсия не оцениваются. В расчётах используются отклонения зависимой переменной yi от её расчётных значений 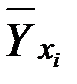 :
:
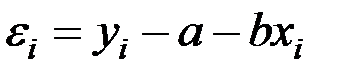 .
.
Так как предполагается, что ошибки (остатки) e i нормально распределены, то среднеквадратическое отклонение ошибок используется для измерения этой вариации.
Среднеквадратические отклонения коэффициентов известны как стандартные ошибки (отклонения):
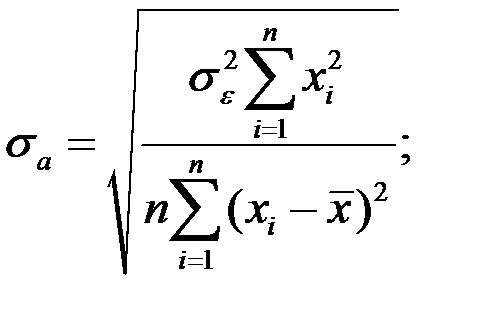
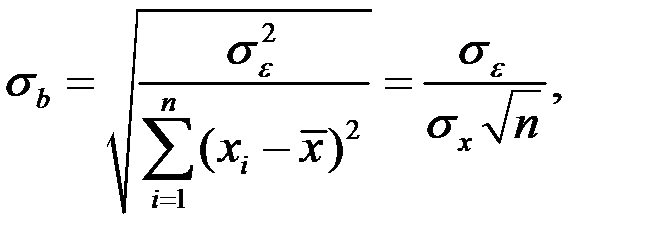
где 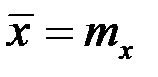 – оценка математического ожидания (среднего значения) независимой переменной Х;
– оценка математического ожидания (среднего значения) независимой переменной Х;
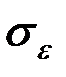 – стандартная ошибка оценки регрессии.
– стандартная ошибка оценки регрессии.
Проверка значимости отдельных коэффициентов регрессии связана с определением наблюдаемых (расчётных) значений Т–критерия (Т–статистики) для соответствующих коэффициентов регрессии.
Нулевая (проверяемая) гипотеза в данном случае имеет вид:
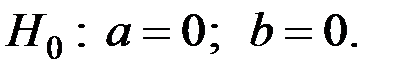
Наблюдаемые значения критерия
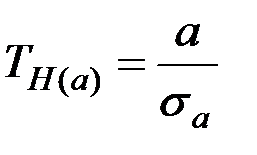 ,
,
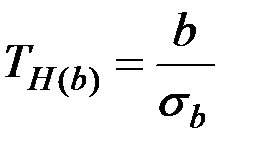
сравниваются с табличными (при двухсторонней критической области)
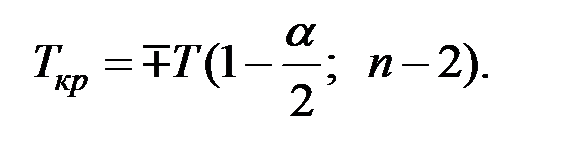
Если расчётное значение критерия 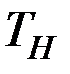 превосходит его табличное значение
превосходит его табличное значение 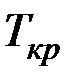 при заданном уровне значимости a (0,1; 0,05; 0,01), коэффициент регрессии считается значимым.
при заданном уровне значимости a (0,1; 0,05; 0,01), коэффициент регрессии считается значимым.
В противном случае фактор, соответствующий этому коэффициенту, следует исключить из модели (при этом её качество не ухудшится).
5. Для значимого уравнения регрессии представляет интерес построение интервальных оценок для параметра b и свободного члена а.
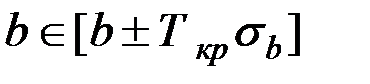 ;
;
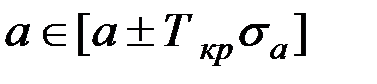 .
.
где 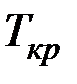 определяется по таблице распределения Стьюдента для уровня значимости a и числа степеней свободы ν = п – 2;
определяется по таблице распределения Стьюдента для уровня значимости a и числа степеней свободы ν = п – 2;
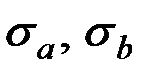 – стандартные отклонения свободного члена и коэффициента регрессии соответственно;
– стандартные отклонения свободного члена и коэффициента регрессии соответственно;
n – число наблюдений.
Пример 5.1. Статистическая обработка 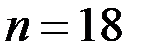 наблюдений показателей (
наблюдений показателей ( 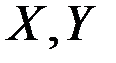 ) дала следующие промежуточные результаты:
) дала следующие промежуточные результаты:
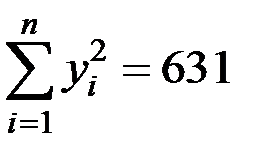 ;
; 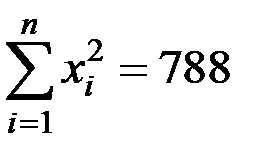 ;
; 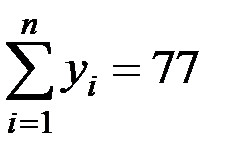 ;
; 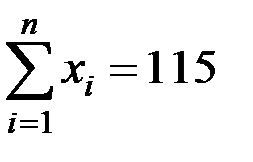 ;
; 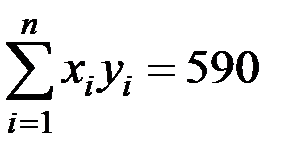 .
.
Определить тесноту связи между показателями и получить уравнение линейной регрессии. Проверить гипотезу о предварительной (экспертной) оценке коэффициента регрессии, предполагаемого равным единице.
Решение. Тесноту связи между показателями оценим с помощью линейного коэффициента корреляции. Для этого вычислим оценки корреляционного момента, дисперсии и средних квадратических отклонений.
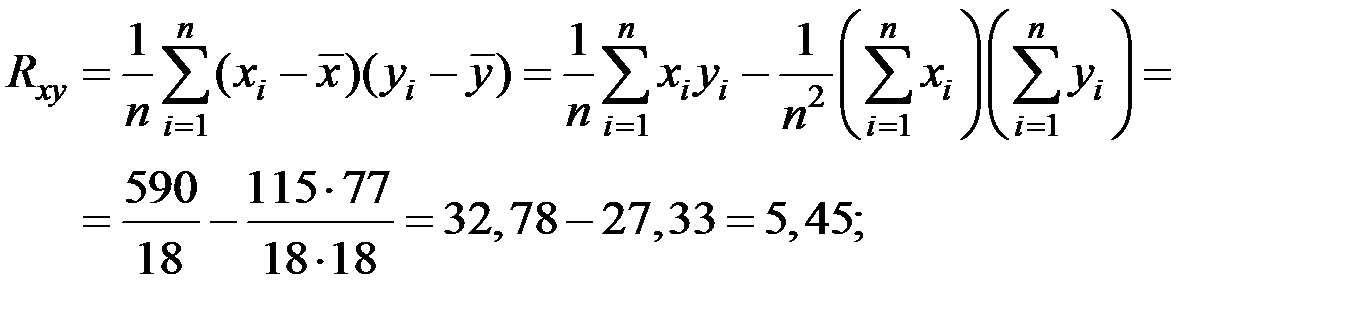
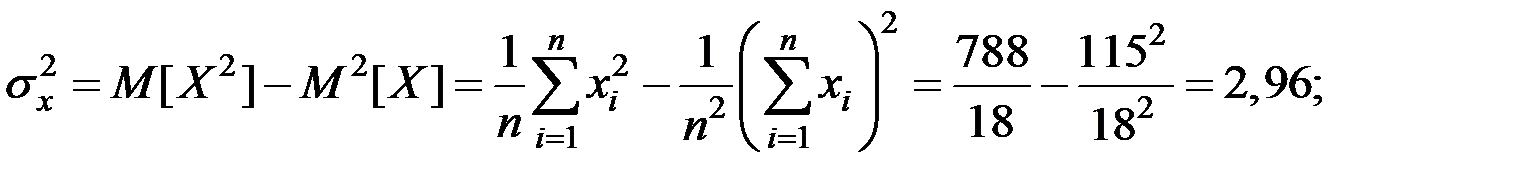
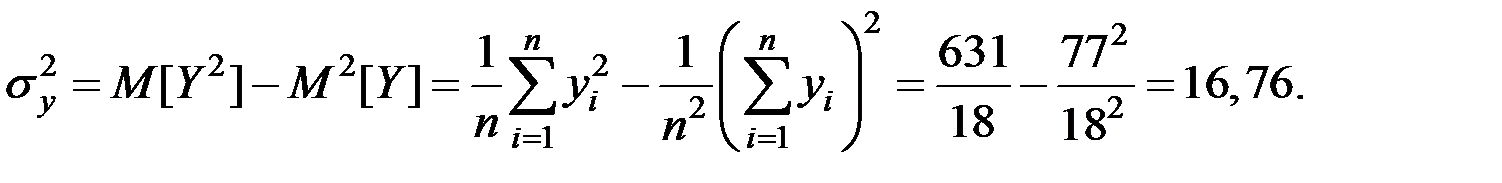
Получаем, что
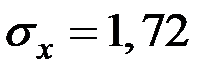 ;
; 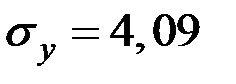 ;
; 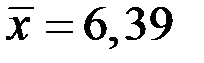 ;
; 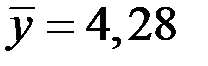 ;
;
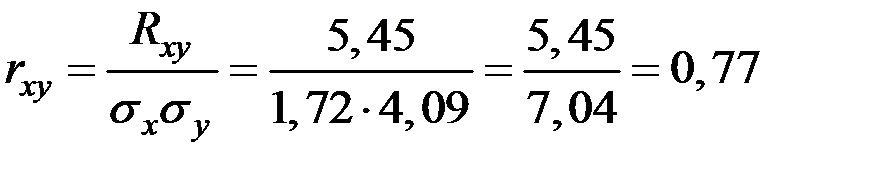 .
.
Уравнение регрессии ищем в виде
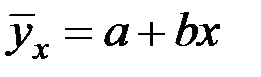 .
.
Оценку параметров регрессии выполним по формулам:
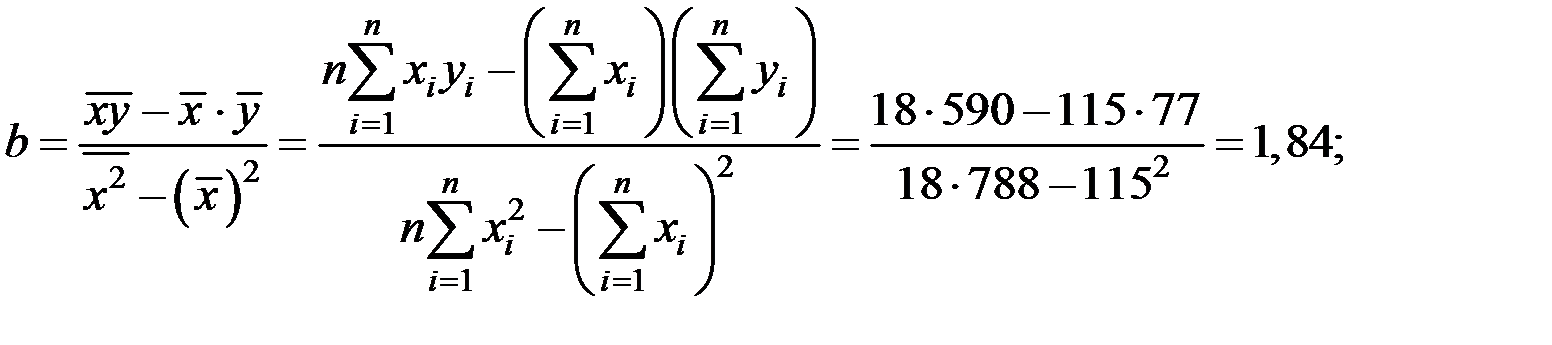
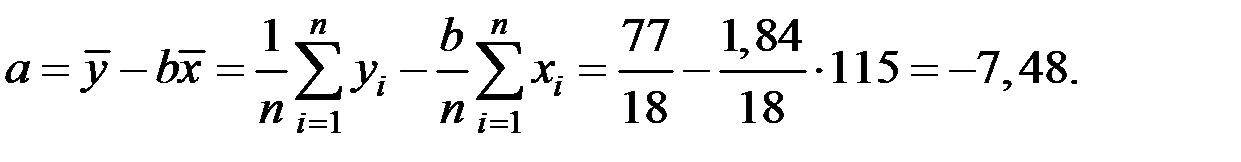
Имеем уравнение:
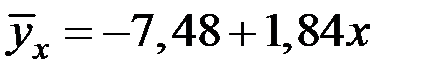 .
.
Вычислим сумму квадратов остатков:
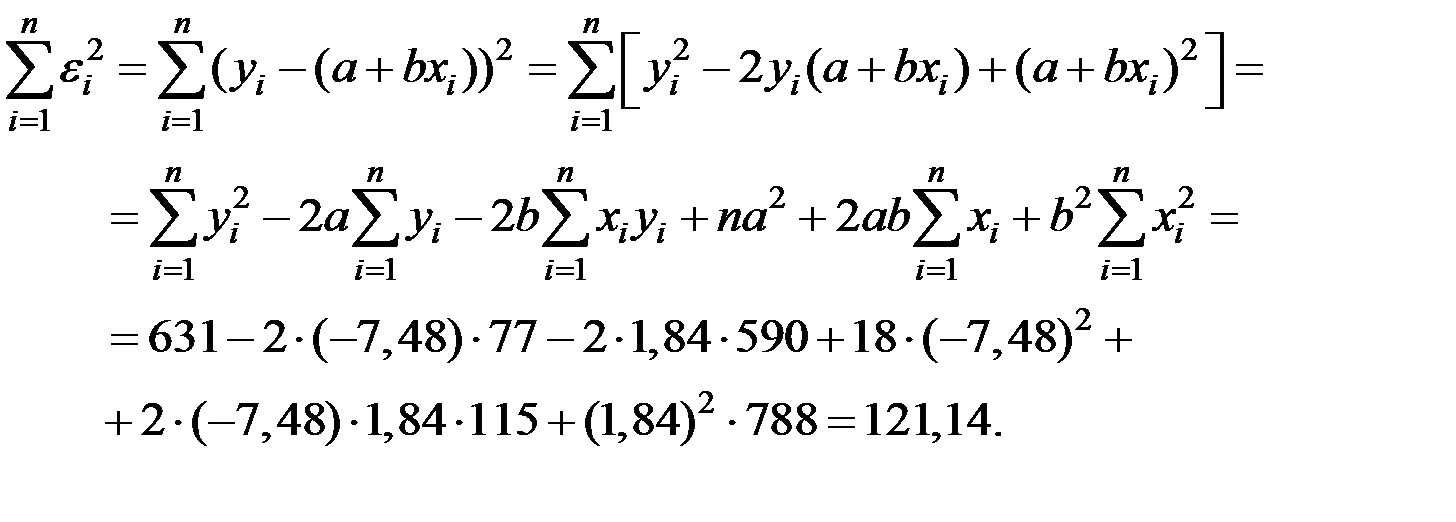
Тогда дисперсия ошибок равна:
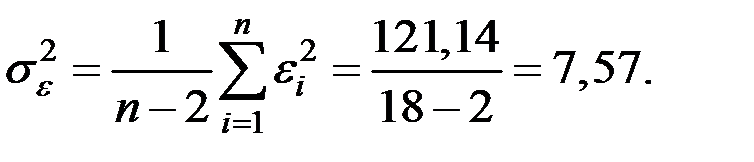
Значит 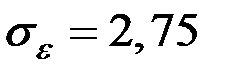 .
.
Проверим гипотезу 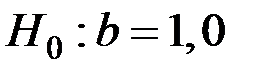 при конкурирующей
при конкурирующей 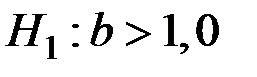 .
.
Дисперсия коэффициента 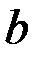 вычисляем по формуле:
вычисляем по формуле:
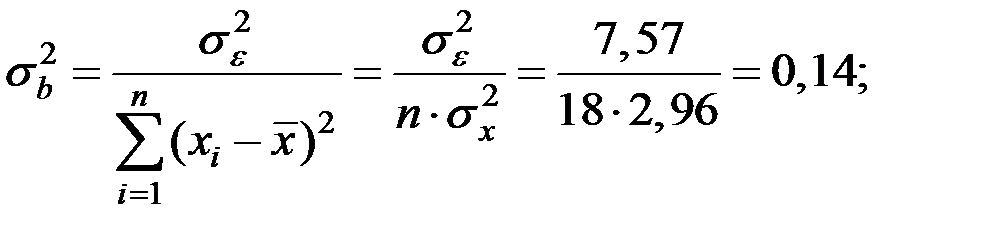 тогда
тогда 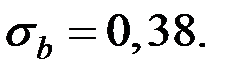
Проверим значимость отклонения коэффициента b:
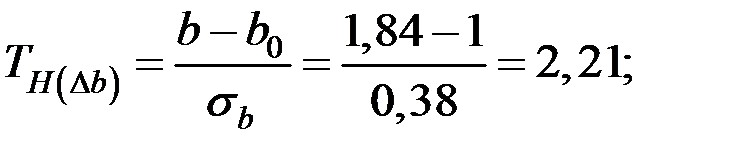
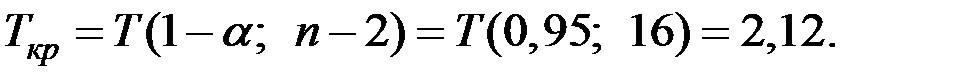
Так как 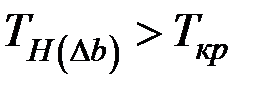 , то гипотезу
, то гипотезу 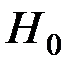 отвергаем, т.е. отклонение коэффициента
отвергаем, т.е. отклонение коэффициента 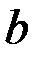 значимо.
значимо.
Проверим значимость коэффициента 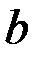 при
при 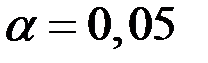 .
.
Проверяемая гипотеза 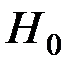 : коэффициент
: коэффициент 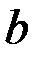 – не значим (
– не значим ( 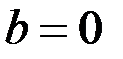 ).
).
Конкурирующая гипотеза 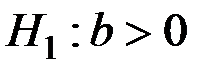 .
.
Тогда
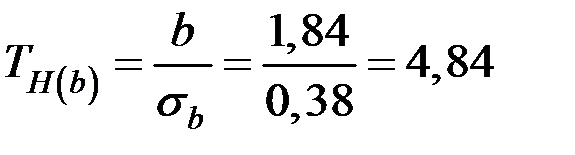 ;
;
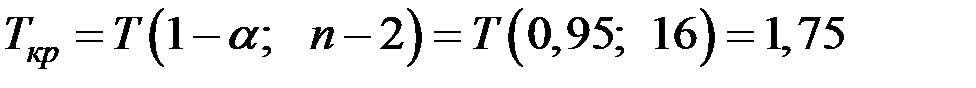 .
.
Так как 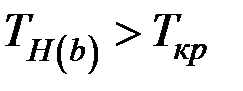 , то коэффициент
, то коэффициент 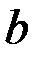 значим.
значим.
Пример 5.2. За прошедший год собраны данные о затратах на рекламу (Х, долл./нед.) и объёме реализации продукции (Y, кг/нед.).
Получили следующие данные:
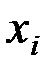 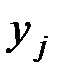
| 1200 – 1300 | 1300 – 1400 | 1400 – 1500 | 1500 – 1600 | 1600 – 1700 |
| 40 – 45 | 1 | ||||
| 45 – 50 | 3 | 2 | 3 | ||
| 50 – 55 | 2 | 4 | 4 | 3 | |
| 55 – 60 | 4 | 5 | 6 | 2 | |
| 60 – 65 | 3 | 4 | 2 | ||
| 65 – 70 | 2 |
Есть ли взаимосвязь между вложениями в рекламу и объёмом продаж? Если взаимосвязь есть, то найти уравнение связи. Спрогнозировать объём продаж, если вложения в рекламу составят 80 долл./нед.
Сколько средств надо вкладывать в рекламу, чтобы получить объём реализации продукции в 1000 кг?
Фирма надеется, что вкладывая в рекламу 100 долл. еженедельно объём реализации продукции составит не менее 2100 кг. Какова вероятность этого?
Решение. Пусть 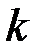 и
и 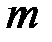 – количество интервалов группировки исходных показателей
– количество интервалов группировки исходных показателей 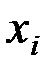 и
и 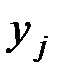 . Имеем:
. Имеем: 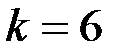 ,
, 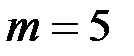 .
.
Тогда общее количество наблюдений
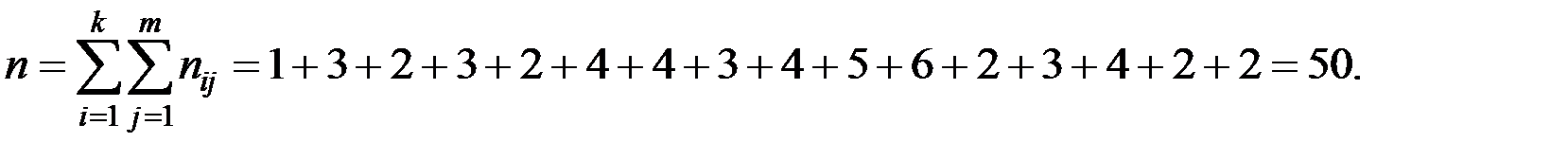
Вычислим основные характеристики, взяв за 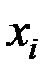 и
и 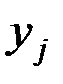 соответствующие середины интервалов:
соответствующие середины интервалов:
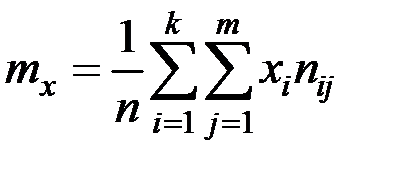 ;
; 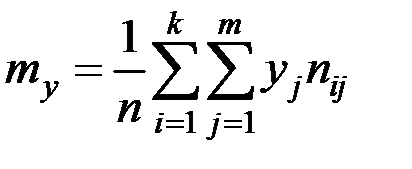 ;
;
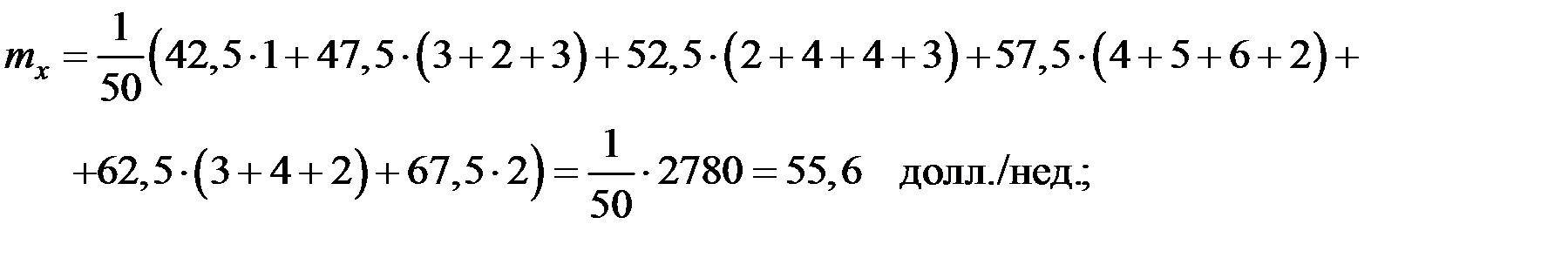
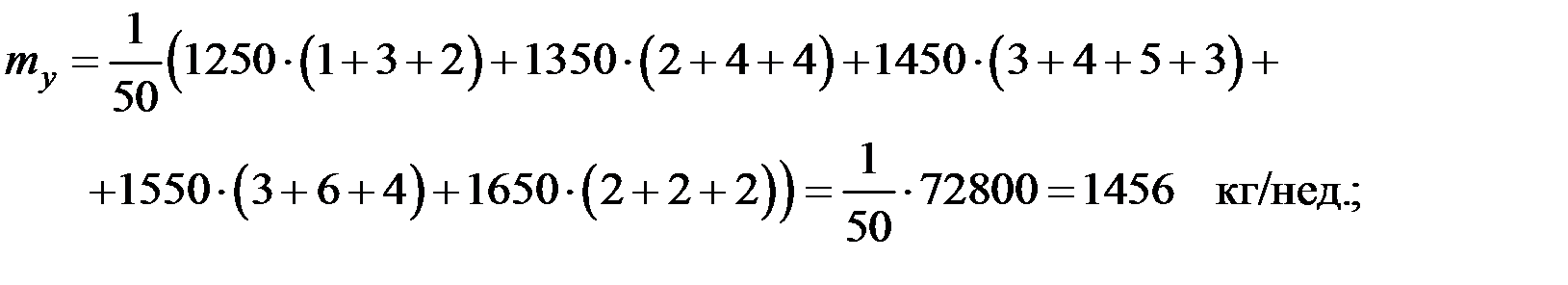
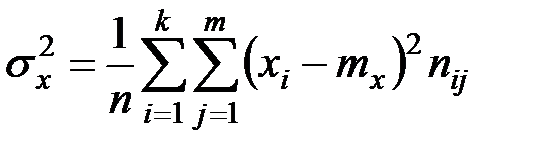 ;
; 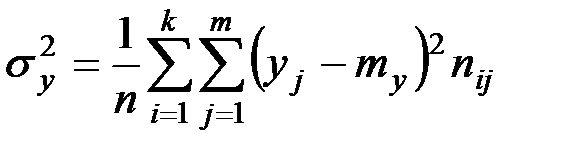 ;
;
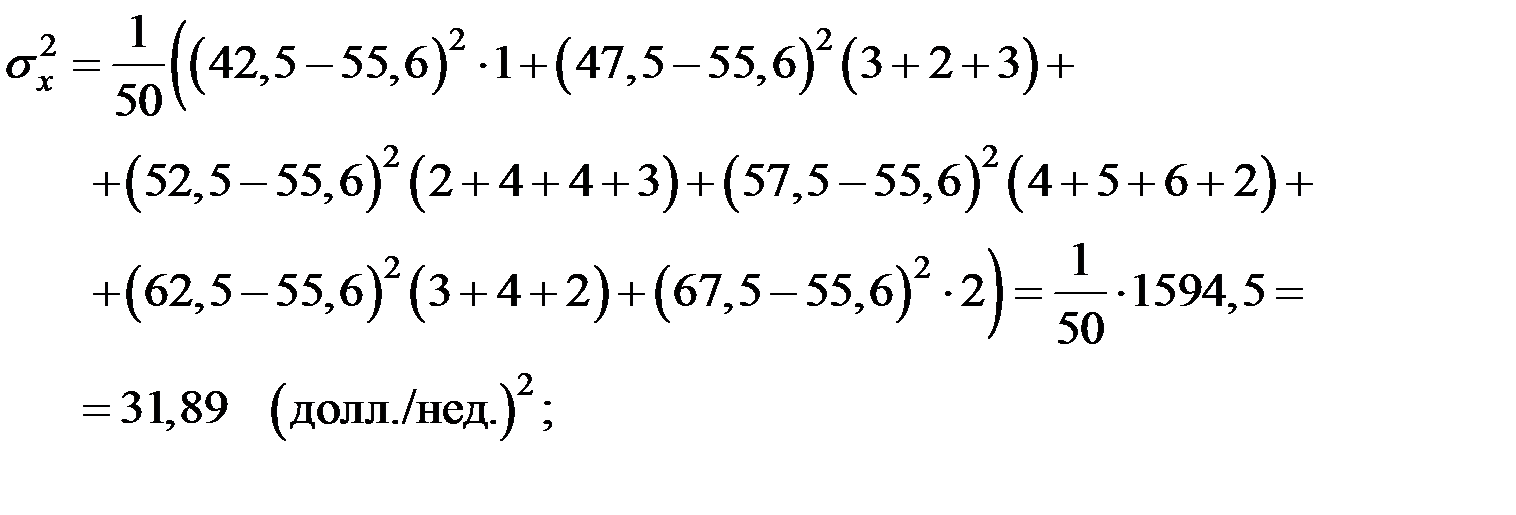
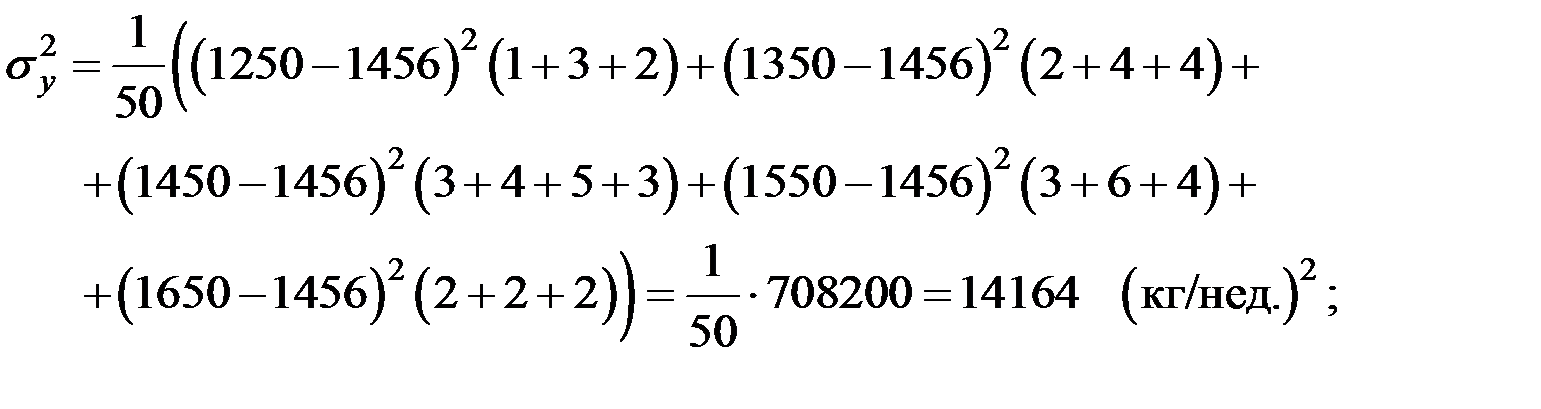
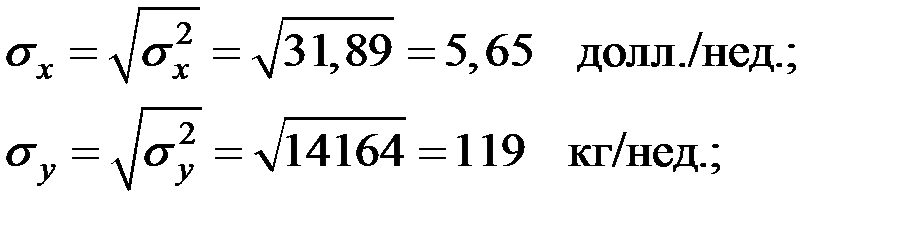

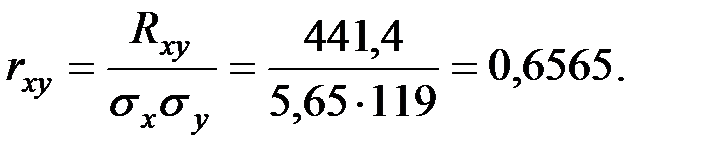
Определим, есть ли взаимосвязь между вложениями в рекламу и объёмом продаж с помощью линейного коэффициента корреляции.
1) Проверка гипотезы о значимости коэффициента корреляции
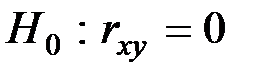
осуществляется с использованием 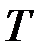 − распределения Стьюдента.
− распределения Стьюдента.
Вычислим наблюдаемое значение критерия:
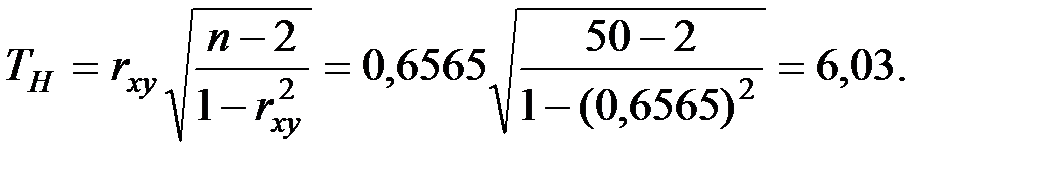
По таблице квантилей 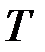 − распределения Стьюдента найдём критическую точку для двухсторонней критической области.
− распределения Стьюдента найдём критическую точку для двухсторонней критической области.
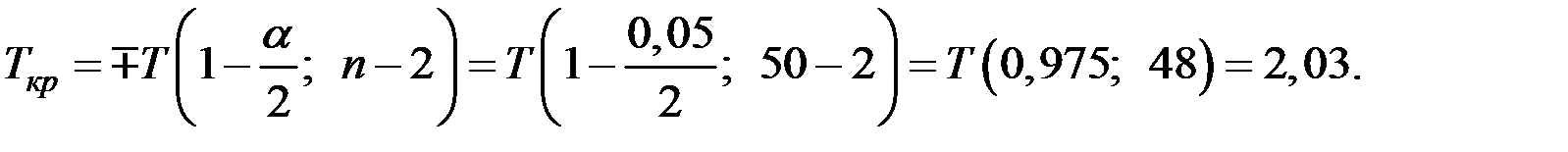
Так как 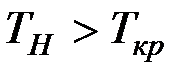 , то гипотезу
, то гипотезу 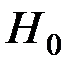 отвергаем, т.е. коэффициент корреляции при уровне значимости
отвергаем, т.е. коэффициент корреляции при уровне значимости 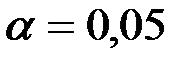 значим.
значим.
2) Получим уравнение регрессии:
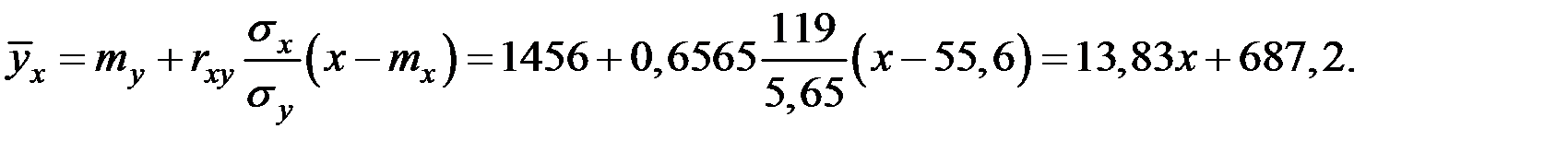

3) Для проверки гипотезы о значимости полученных моделей регрессии ( 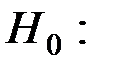 уравнение не значимо) вычислим значение
уравнение не значимо) вычислим значение 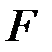 –критерия:
–критерия:
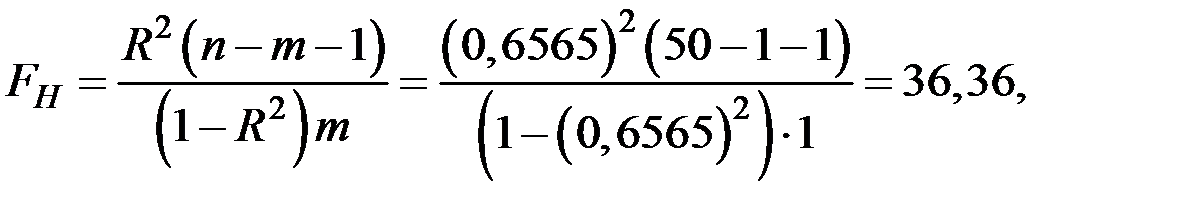
где 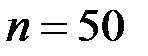 – количество наблюдений,
– количество наблюдений, 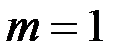 – количество показателей.
– количество показателей.
По таблице квантилей 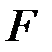 – распределения найдём критическую точку.
– распределения найдём критическую точку.
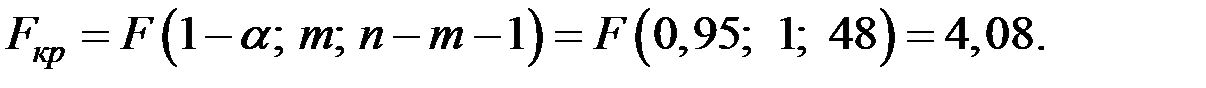
Так как 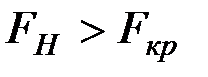 , то гипотезу
, то гипотезу 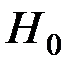 отвергаем, т.е. уравнения регрессии значимы при уровне значимости
отвергаем, т.е. уравнения регрессии значимы при уровне значимости 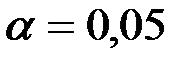 .
.
4) Прогнозную величину еженедельных продаж, если расходы на рекламу составят 80 долл./нед., определим по уравнению регрессии:
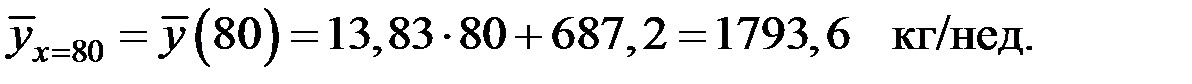
5) По уравнению регрессии для 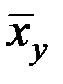 вычислим сколько надо вкладывать в рекламу, чтобы объём продаж составил 1000 долл./нед.
вычислим сколько надо вкладывать в рекламу, чтобы объём продаж составил 1000 долл./нед.
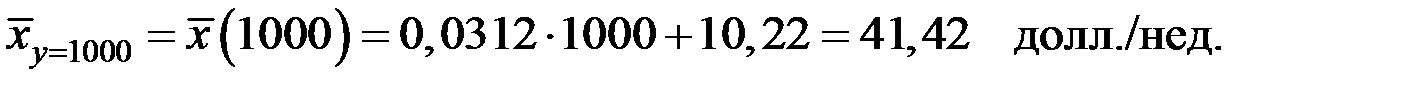
6) Определим объём реализации при х =100 долл.
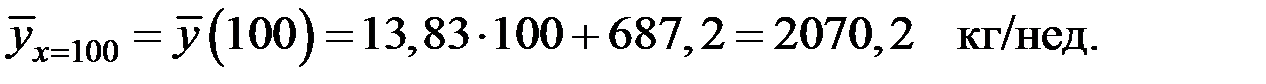
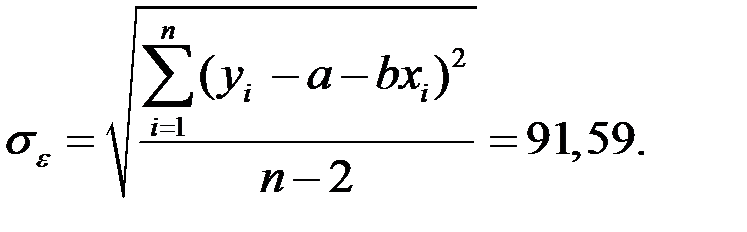
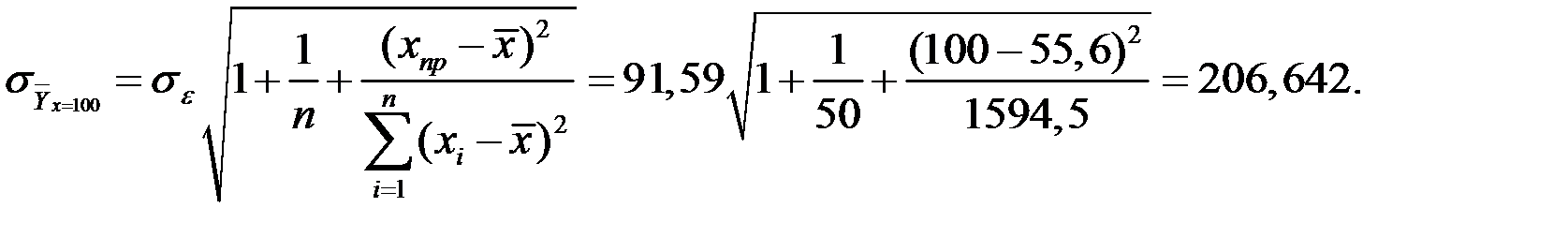
Тогда вероятность того, что 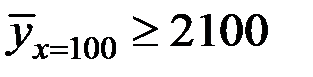
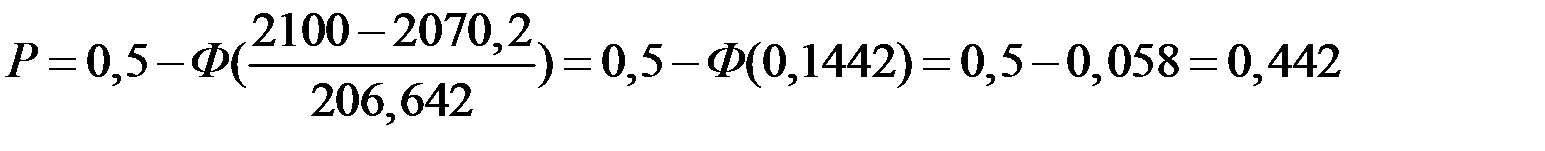 .
.
Пример 5.3. Месячные объёмы продаж ткани ( 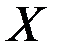 , тыс. м.) и величины премиального фонда (
, тыс. м.) и величины премиального фонда ( 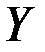 , тыс. руб.) в девяти филиалах торговой фирмы характеризовались следующими данными:
, тыс. руб.) в девяти филиалах торговой фирмы характеризовались следующими данными:
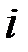
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
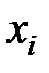
| 2,3 | 2,8 | 1,9 | 3,4 | 2,6 | 3,3 | 4,2 | 3,0 | 1,7 |
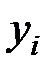
| 6,1 | 8,2 | 7,1 | 14,9 | 9,1 | 9,0 | 15,8 | 8,2 | 7,7 |
Исследовать зависимость премиального фонда от объёма продаж.
Получить прогноз объёма премиального фонда при продажах 3,4 тыс. м ткани. Оценить качество прогноза.
Продавцы полагают, что если объём продаж составит 5 тыс. метров, то их премия будет свыше 18 тыс. руб. в месяц. Какова вероятность этого?
Решение.
1. Найдём основные характеристики исследуемых величин:
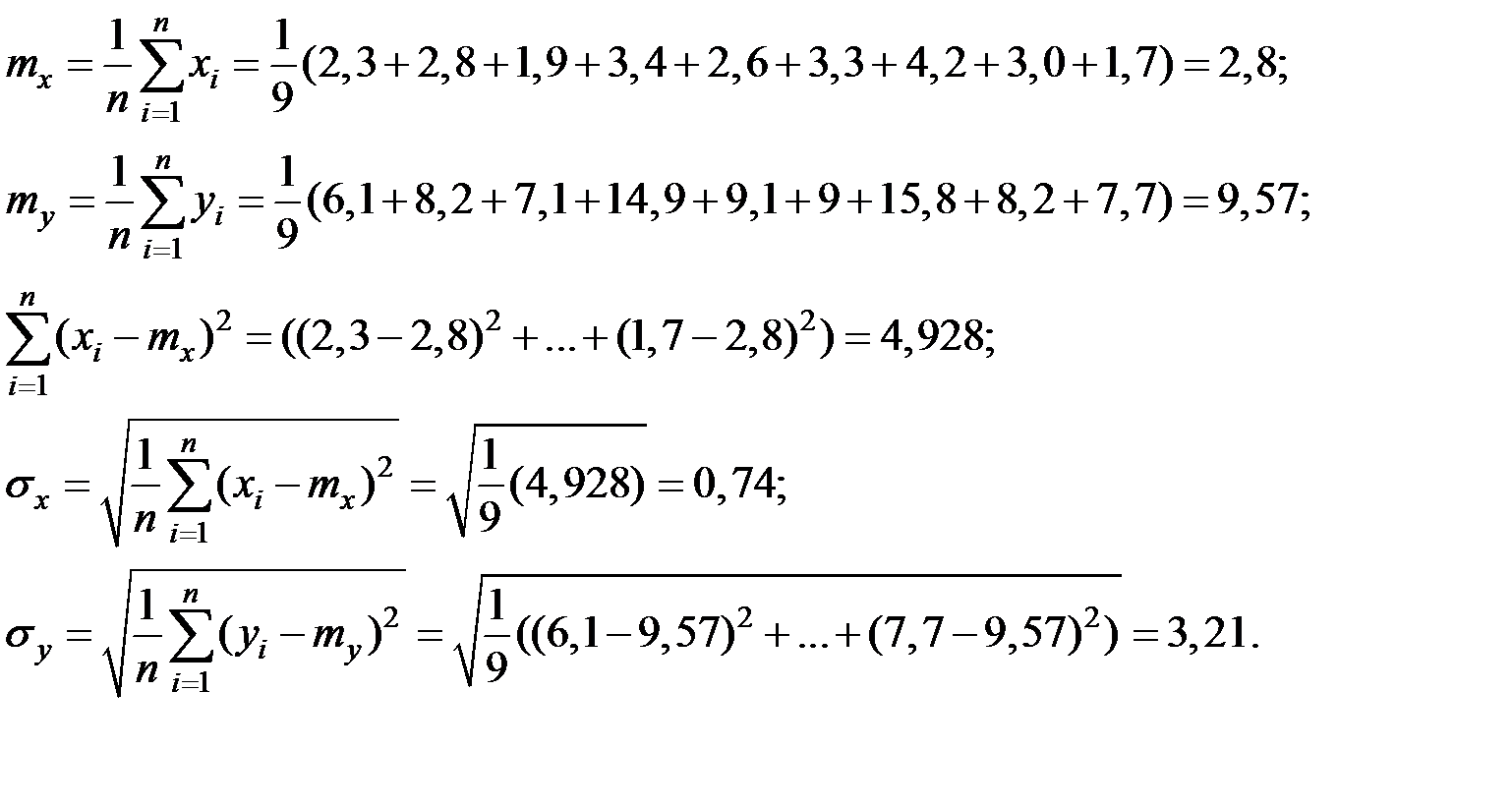
2. Исследуем тесноту линейной зависимости показателей.
Вычислим корреляционный момент показателей 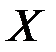 и
и 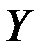 .
.
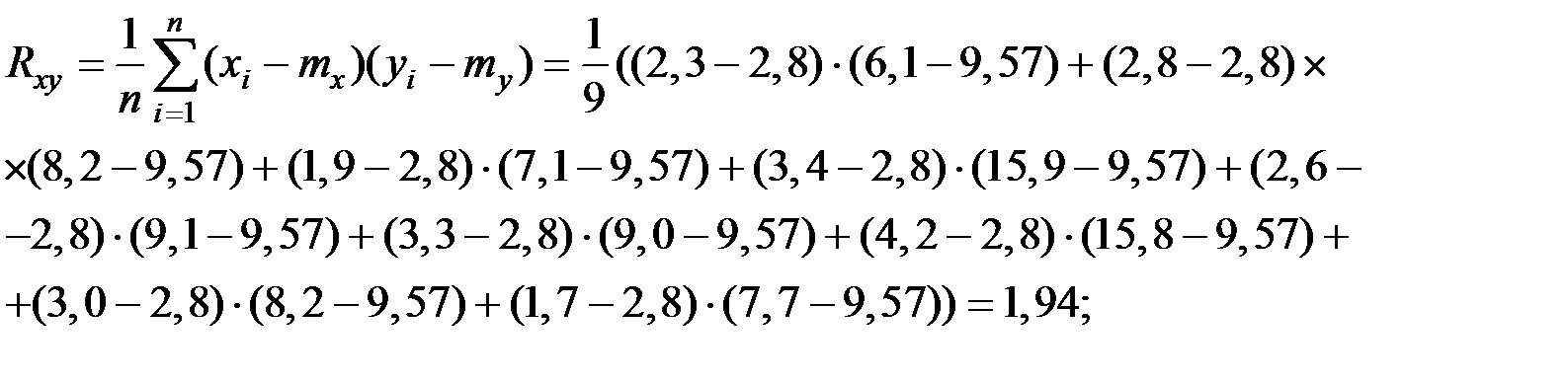
Линейный коэффициент корреляции:
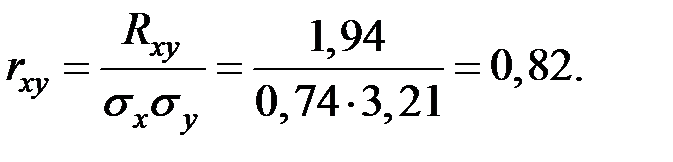
Исследуем найденный коэффициент на значимость.
Воспользуемся 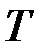 – критерием Стьюдента.
– критерием Стьюдента.
Гипотеза 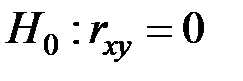 , конкурирующая гипотеза
, конкурирующая гипотеза 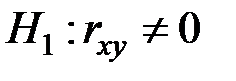 .
.
Возьмём уровень значимости 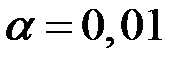 .
.
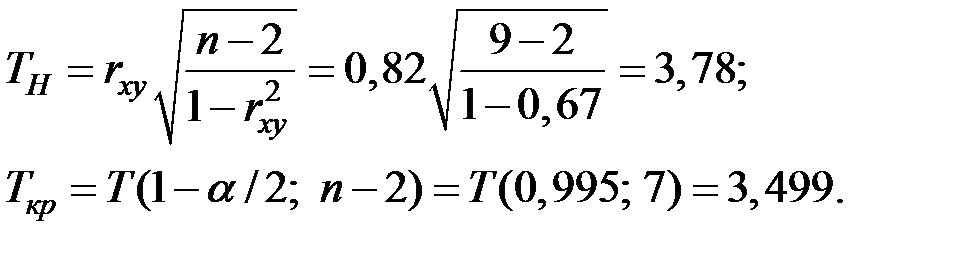
Так как 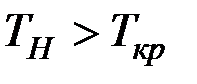 , то принимаем гипотезу
, то принимаем гипотезу 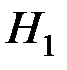 , т.е. линейный коэффициент корреляции значим, и между
, т.е. линейный коэффициент корреляции значим, и между 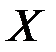 и
и 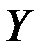 существует линейная зависимость.
существует линейная зависимость.
3. Найдём линейную зависимость в виде:
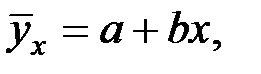
где 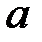 и
и 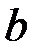 находятся по формулам:
находятся по формулам:
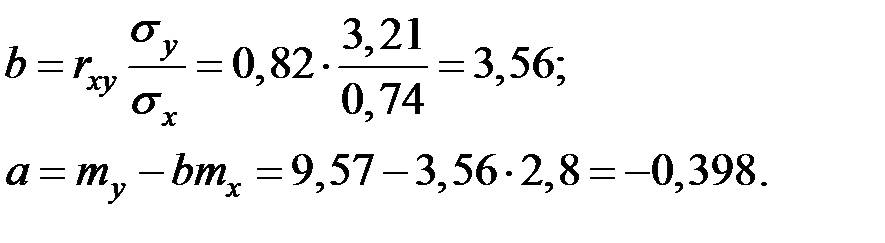
Уравнение регрессии имеет вид: 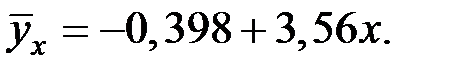
Вычислим значения 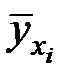 по полученному уравнению регрессии:
по полученному уравнению регрессии:
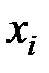
| 2,300 | 2,800 | 1,900 | 3,400 | 2,600 | 3,300 | 4,200 | 3,000 | 1,700 |
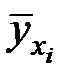
| 7,790 | 9,570 | 6,366 | 11,706 | 8,858 | 11,350 | 14,554 | 10,282 | 5,654 |
Проверим полученное уравнение регрессии на значимость при уровне значимости 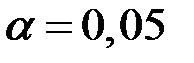 . Для этого воспользуемся
. Для этого воспользуемся 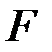 −критерием.
−критерием.
Гипотеза 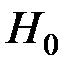 : уравнение не значимо, конкурирующая гипотеза
: уравнение не значимо, конкурирующая гипотеза 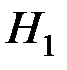 : уравнение значимо.
: уравнение значимо.
Вычислим значение критерия по формуле:
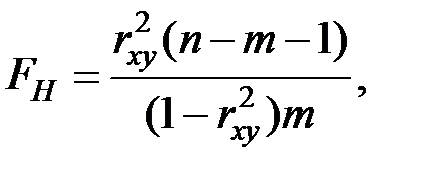
где 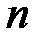 − количество наблюдений,
− количество наблюдений,
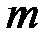 − количество независимых переменных
− количество независимых переменных 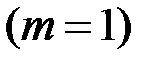 .
.
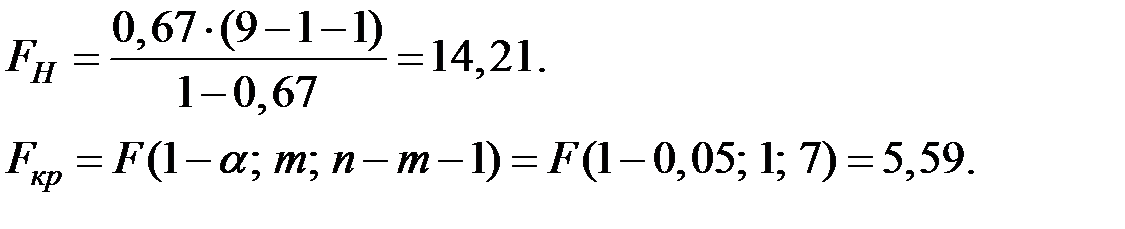
Так как 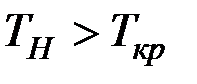 , то принимаем гипотезу
, то принимаем гипотезу 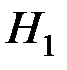 , т.е. уравнение регрессии значимо.
, т.е. уравнение регрессии значимо.
Проверим на значимость коэффициенты уравнения регрессии.
Для этого вычислим стандартную ошибку по соотношению
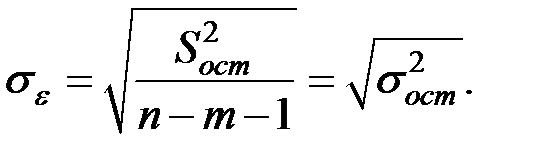
Вычислим соответствующую сумму квадратов отклонений.
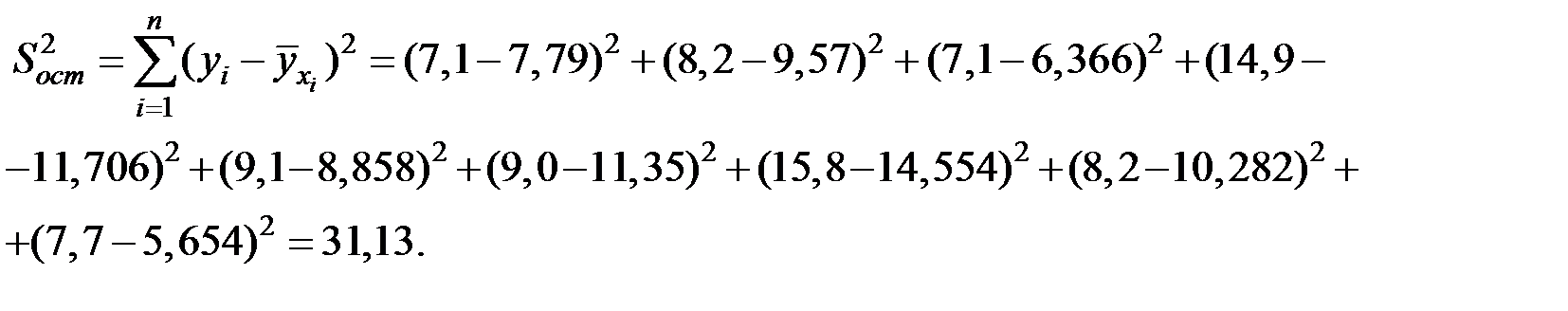
Тогда:
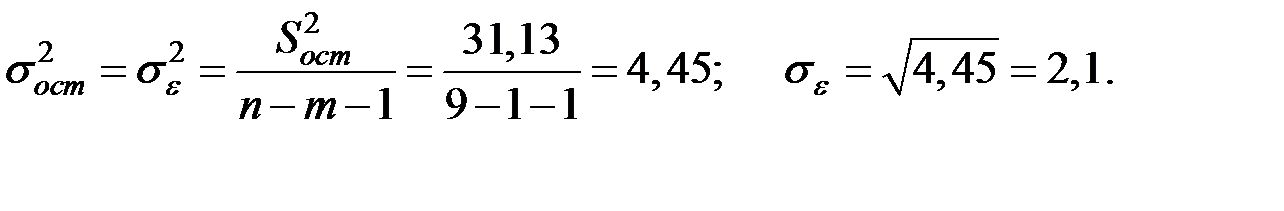
Проверим на значимость коэффициент 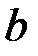 .
.
Гипотеза 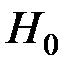 : коэффициент
: коэффициент 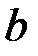 не значим (
не значим ( 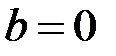 ), конкурирующая гипотеза
), конкурирующая гипотеза 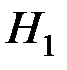 : коэффициент
: коэффициент 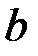 значим (
значим ( 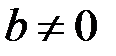 ).
).
Возьмём уровень значимости 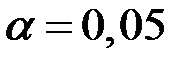 .
.
Вычислим наблюдаемое значение критерия по формуле:
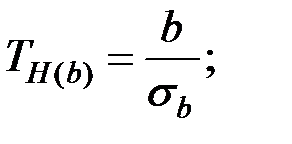
где 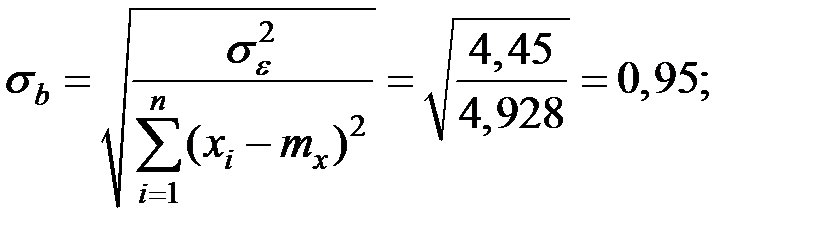
Тогда
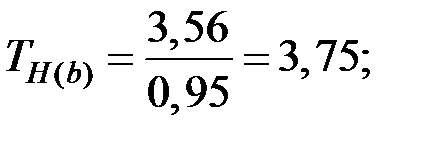
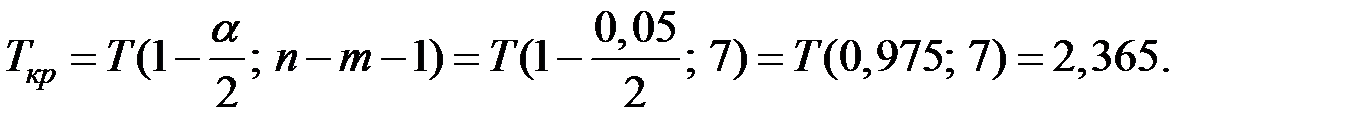
Так как 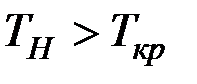 , то принимаем гипотезу
, то принимаем гипотезу 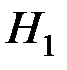 : коэффициент
: коэффициент 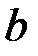 значим.
значим.
Для коэффициента 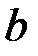 можно получить доверительный интервал:
можно получить доверительный интервал:
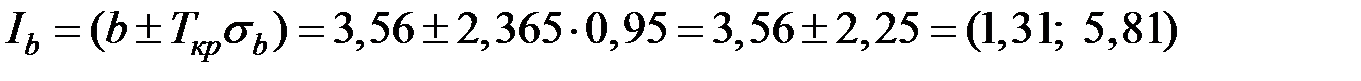
для 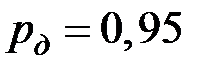 .
.
Проверим на значимость коэффициент 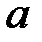 .
.
Гипотеза 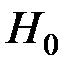 : (
: ( 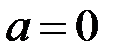 ), конкурирующая гипотеза
), конкурирующая гипотеза 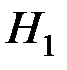 : (
: ( 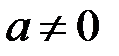 ).
).
Вычислим значение критерия по формуле:
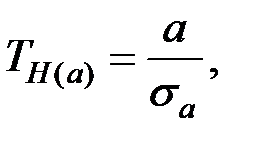
где 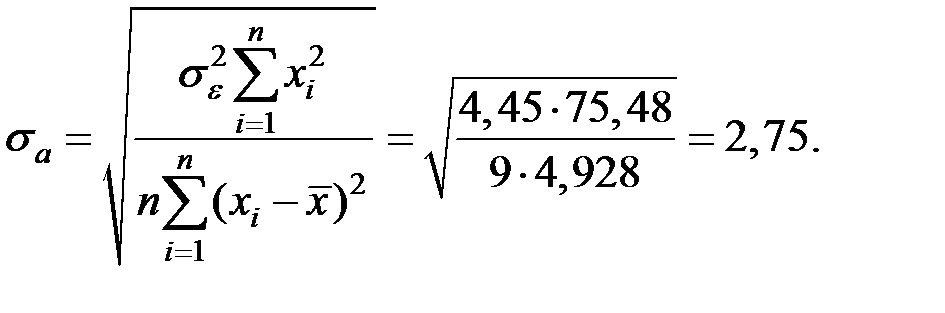
Тогда
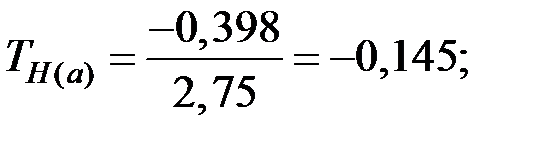
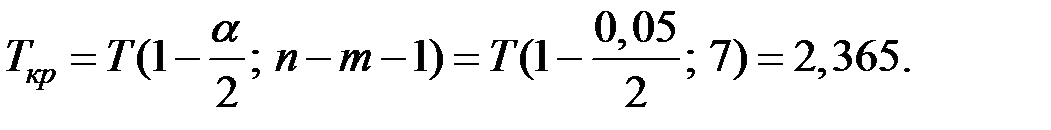
Так как 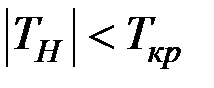 , то нет оснований отвергать гипотезу
, то нет оснований отвергать гипотезу 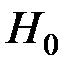 , т.е. коэффициент
, т.е. коэффициент 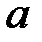 не значим.
не значим.
4. Получим прогноз объёма премиального фонда при 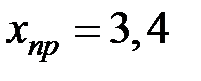 .
.
По уравнению регрессии найдём:
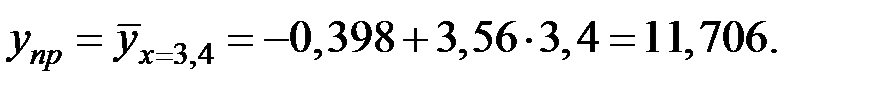
Получим доверительный интеграл для уравнения регрессии:
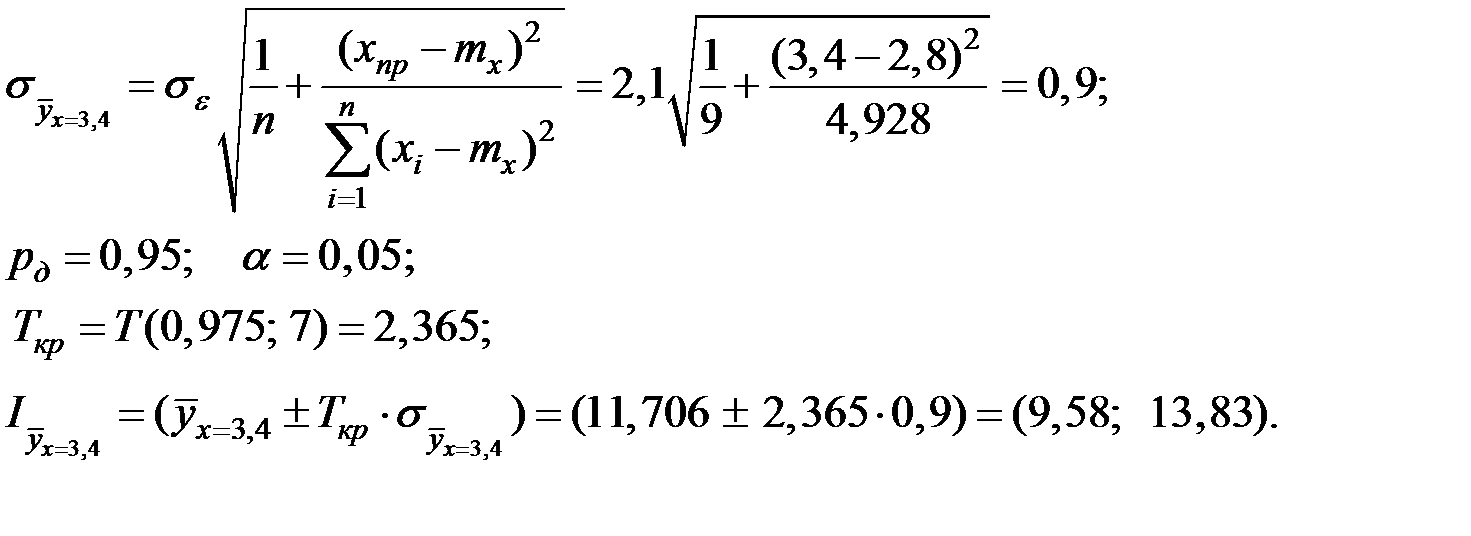
5. Получим прогноз объёма премиального фонда при 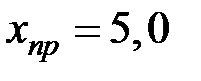 .
.
По уравнению регрессии найдём:
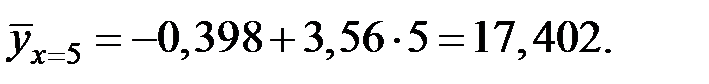
Доверительный интервал для данного индивидуального прогноза:
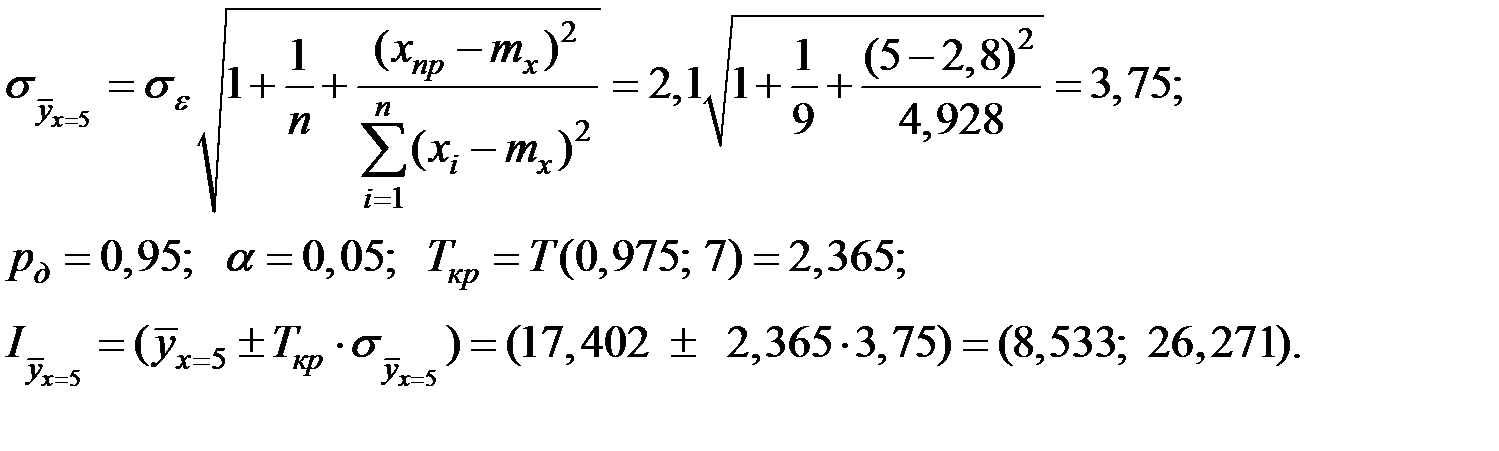
Искомую вероятность определим с использованием условного нормального закона распределения с параметрами
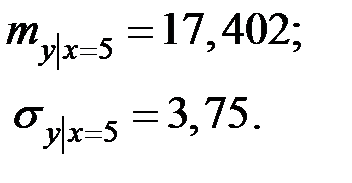
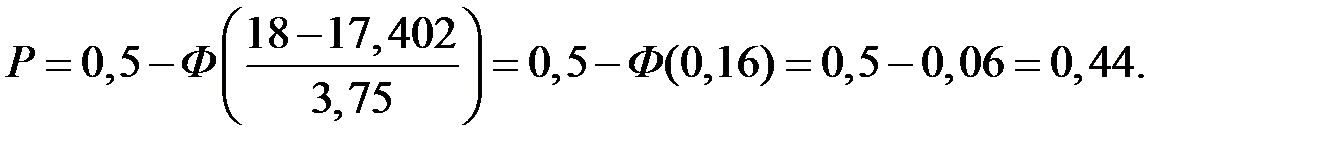
Нелинейная парная регрессия
Если между явлениями существуют нелинейные соотношения, то они выражаются с помощью соответствующих нелинейных функций.
Различают 2 класса моделей нелинейных регрессий:
1) регрессии, нелинейные относительно переменных, но линейные по параметрам (полиномы разных степеней, гипербола и др.);
2) регрессии, нелинейные по оцениваемым параметрам (степенная, показательная, экспоненциальная и др.);
Параметры уравнения регрессии, нелинейного относительно переменных, определяются (как и линейного) на основе МНК.
Так в случае поиска уравнения регрессии в виде полинома k–й степени, исходя из основного принципа МНК
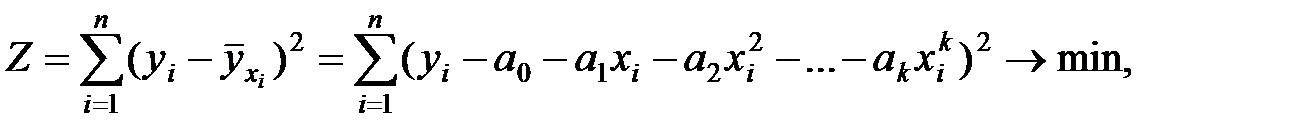
вычисляя и приравнивая частные производные критерия Z по каждому неизвестному параметру к нулю ( 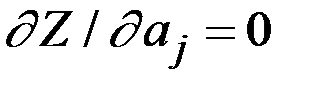 ), получим систему уравнений
), получим систему уравнений
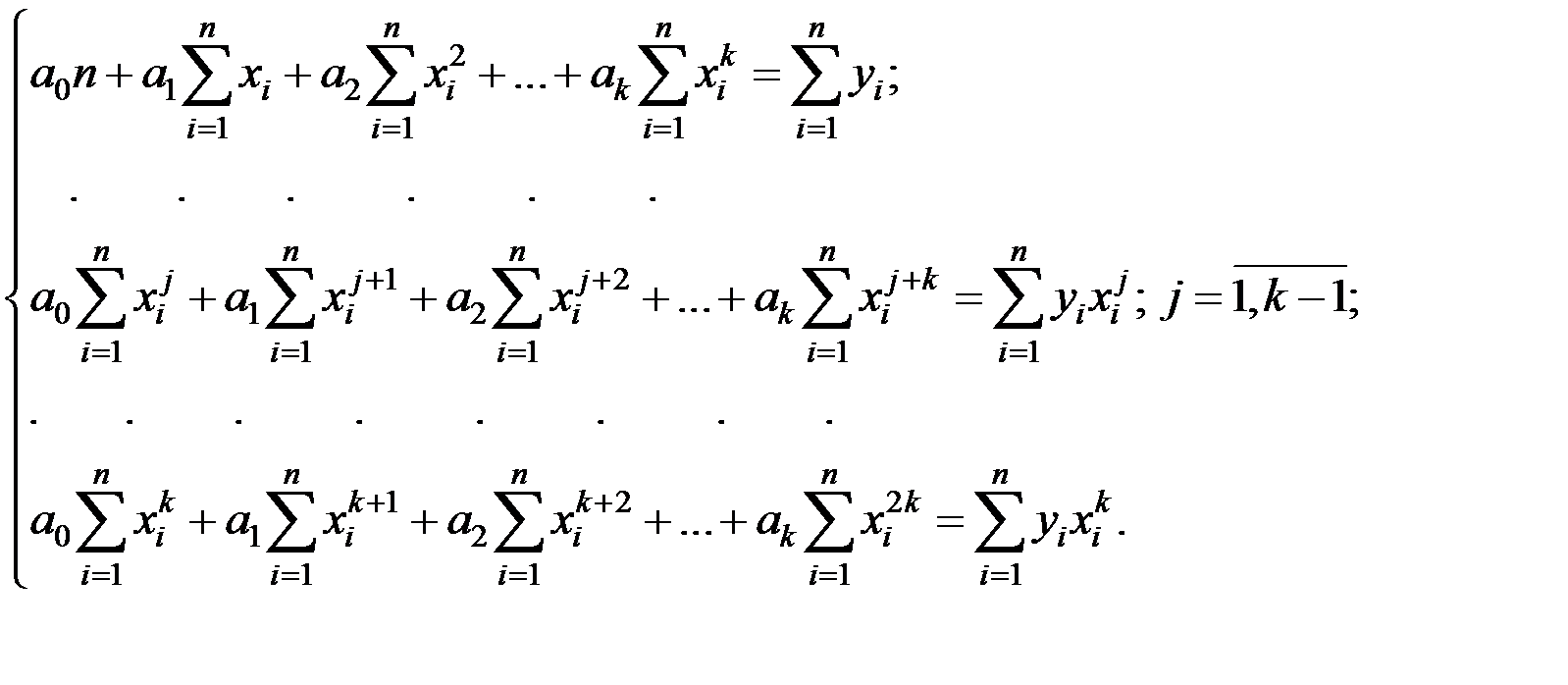
Решая эту систему, найдём неизвестные параметры 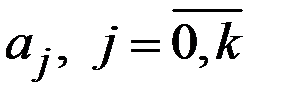 .
.
Регрессии, нелинейные по оцениваемым параметрам, подразделяются на:
1) нелинейные модели внутренне линейные;
2) нелинейные модели внутренне нелинейные.
Если модель нелинейна относительно параметров регрессии, то она в ряде случаев с помощью соответствующих преобразований может быть приведена к линейному виду (табл. 5.1)
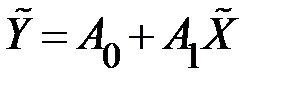 .
.
Если же модель внутренне нелинейная, то она не может быть приведена к линейному виду.
Для оценки параметров в этом случае используются итеративные (итерационные) процедуры, успешность которых зависит от вида уравнения и особенностей применяемого метода.
Таблица 5.1
Подстановки для перехода от нелинейных зависимостей к линейным
| № | Вид нелинейной зависимости | Подстановка |
| 1 | 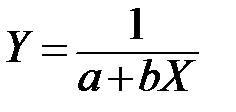
| 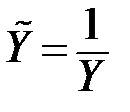
|
| 2 | 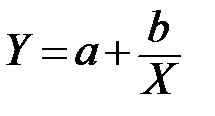
| 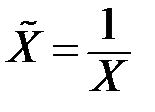
|
| 3 | 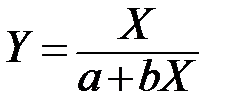
| 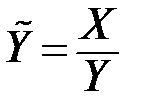
|
| 4 | 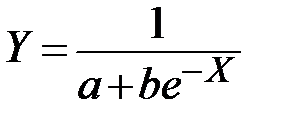
| 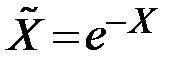 ; ; 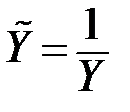
|
| 5 | 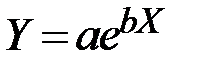
| 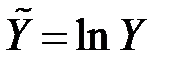
|
| 6 | 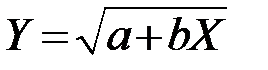
| 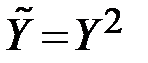
|
| 7 | 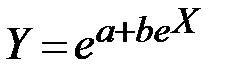
| 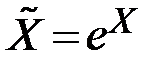 ; ; 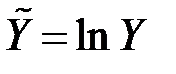
|
| 8 | 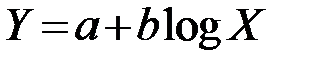
| 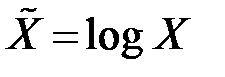
|
| 9 | 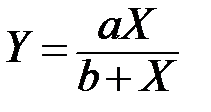
| 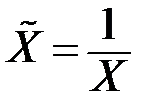 ; ; 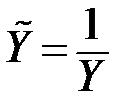
|
Пример 5.4. Исследовать зависимость урожайности капусты Y (ц/га) от количества использованной воды при искусственном поливе X (м3/га) в период роста культур.
Опытные данные по 9 полям представлены ниже в таблице:
| № поля | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
Кол–во воды при поливе 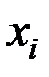 (м3/га) (м3/га)
| 18,2 | 16,3 | 17,0 | 19,4 | 20,4 | 22,1 | 23,2 | 24,3 | 25,1 |
Урожайность 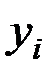 (ц/га) (ц/га)
| 25,3 | 23,1 | 24,2 | 30,5 | 35,6 | 33,7 | 30,8 | 28,2 | 22,5 |
Выполнить регрессионный анализ исследуемых переменных.
Решение. Можно предположить, что увеличение объёма полива приводит к урожайности до некоторого предела, после чего урожайность будет снижаться.
С учётом расположения точек корреляционного поля (таблица) можно предположить, что наиболее подходящим уравнением регрессии будет уравнение параболы: 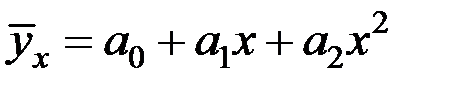 .
.
Параметры модели ( 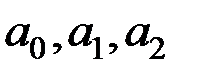 ) находим, используя МНК:
) находим, используя МНК:
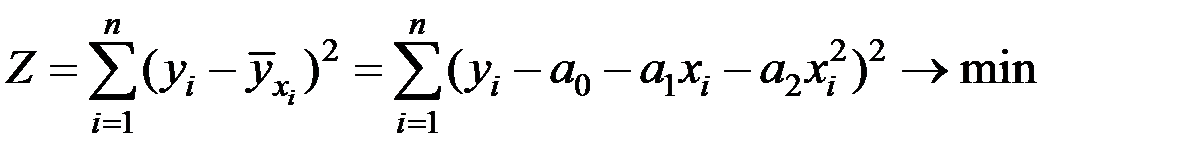 .
.
Приравняв частные производные критерия по неизвестным параметрам к нулю 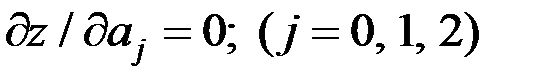 , получим (после соответствующих преобразований) систему нормальных уравнений:
, получим (после соответствующих преобразований) систему нормальных уравнений:
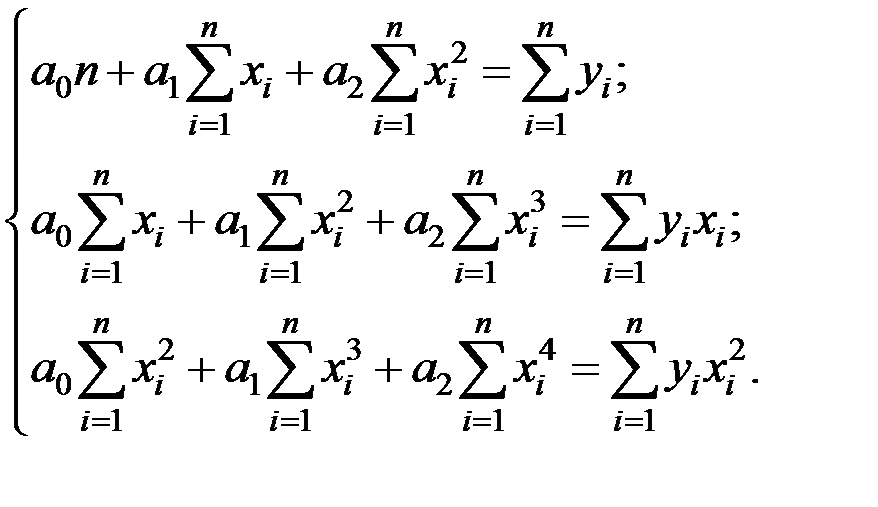
Для расчёта необходимых сумм составим вспомогательную таблицу:
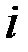
| 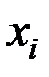
| 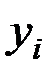
| 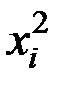
| 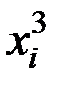
| 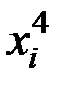
|
| 1 | 18,2 | 25,3 | 331,2 | 6028,6 | 109719,9 |
| 2 | 16,3 | 23,1 | 265,7 | 4330,7 | 70591,2 |
| 3 | 17,0 | 24,2 | 289,0 | 4913,0 | 83521,0 |
| 4 | 19,4 | 30,5 | 376,4 | 7301,4 | 141646,9 |
| 5 | 20,4 | 35,6 | 416,2 | 8489,7 | 173189,1 |
| 6 | 22,1 | 33,7 | 488,4 | 10793,9 | 238544,4 |
| 7 | 23,2 | 30,8 | 538,2 | 12487,2 | 289702,3 |
| 8 | 24,3 | 28,2 | 590,5 | 14348,9 | 348678,4 |
| 9 | 25,1 | 22,5 | 630,0 | 15813,3 | 396912,6 |
| Итого | 186,0 | 253,9 | 3925,6 | 84506,6 | 1852505,8 |
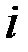
| 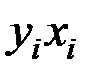
| 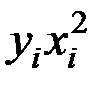
| 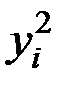
| 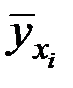
| 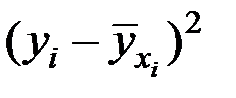
|
| 1 | 460,5 | 8380,4 | 640,1 | 29,0 | 13,7 |
| 2 | 376,5 | 6137,4 | 533,6 | 20,9 | 4,8 |
| 3 | 411,4 | 6993,8 | 585,6 | 24,4 | 0,1 |
| 4 | 591,7 | 11479,0 | 930,3 | 32,0 | 2,3 |
| 5 | 726,2 | 14815,3 | 1267,4 | 33,3 | 5,3 |
| 6 | 744,8 | 16459,4 | 1135,7 | 32,8 | 0,8 |
| 7 | 714,6 | 16577,8 | 948,6 | 30,8 | 0,0 |
| 8 | 685,3 | 16651,8 | 795,2 | 27,4 | 0,6 |
| 9 | 564,8 | 14175,2 | 506,3 | 24,0 | 2,3 |
| Итого | 5275,7 | 111670,1 | 7342,8 | 254,6 | 29,8 |
Теперь система уравнений примет вид:
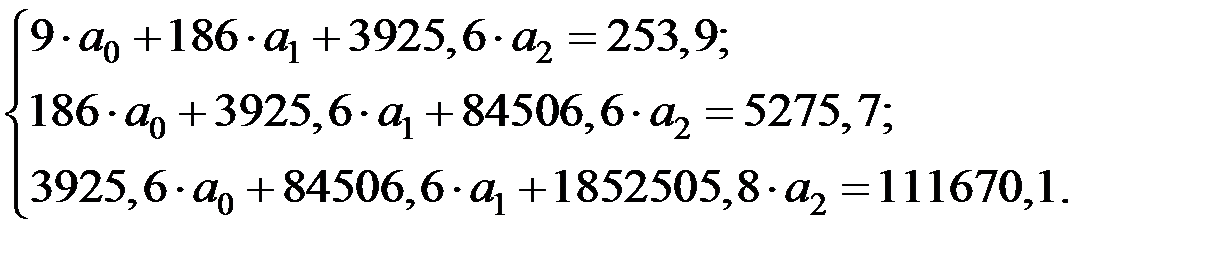
Решая эту систему (например, методом Гаусса) получим:
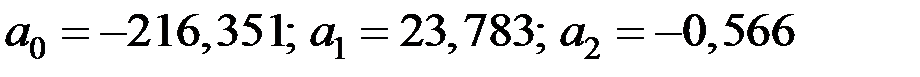
Уравнение регрессии будет иметь вид:
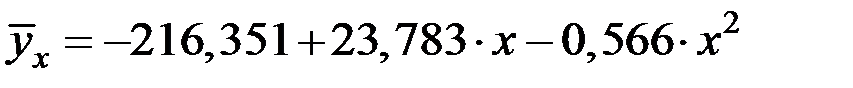
1. Оценим значимость (адекватность) полученной модели.
Вычислим необходимые суммы квадратов отклонений.
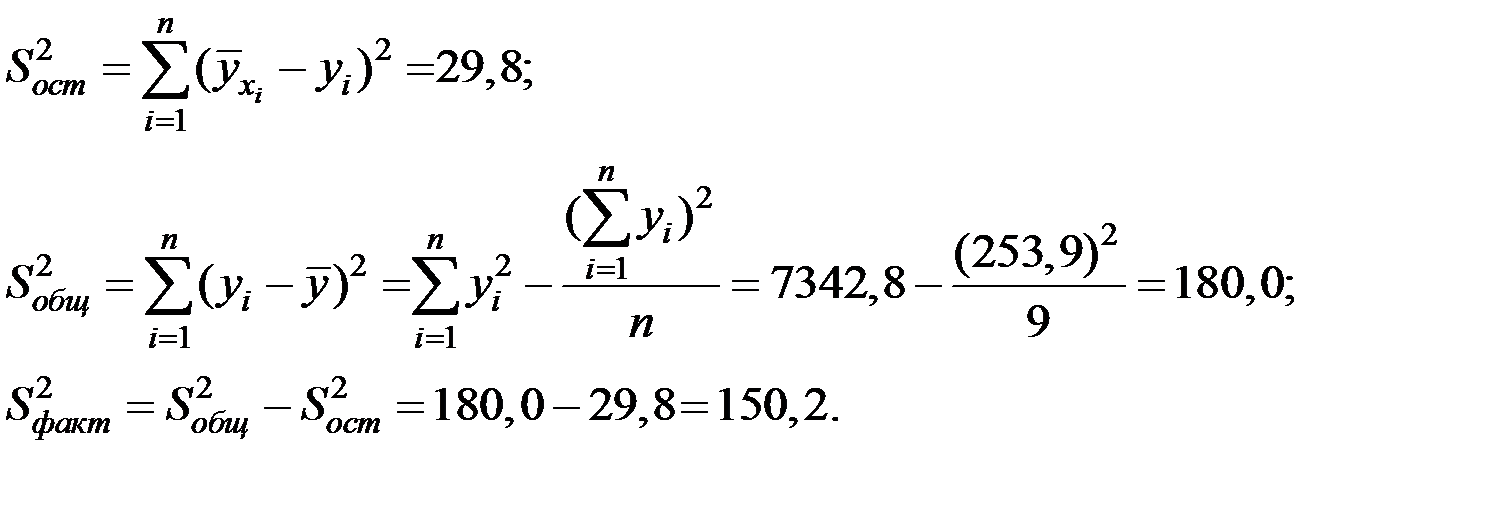
Тогда значение критерия адекватности модели будет равно:
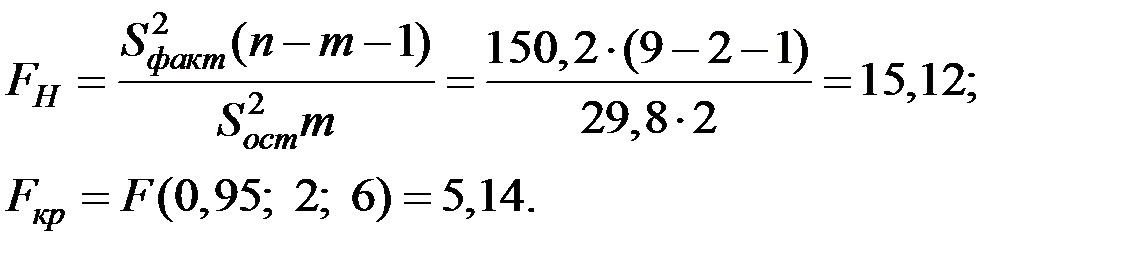
Здесь m – количество параметров при независимой переменной (m = 2).
Уравнение регрессии значимо.
2. Для оценки тесноты связи между переменными X и Y вычислим индекс корреляции:
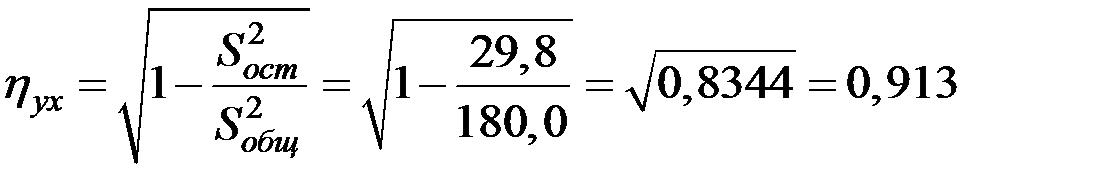 .
.
Полученная зависимость весьма веская и значимая.
Коэффициент детерминации 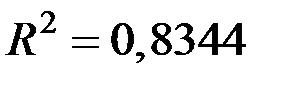 показывает, что вариация урожайности зерновых культур на 83,44% обусловлена регрессией, т.е. изменчивостью количества воды при поливе.
показывает, что вариация урожайности зерновых культур на 83,44% обусловлена регрессией, т.е. изменчивостью количества воды при поливе.
3. Точность модели оценим стандартной ошибкой уравнения регрессии: 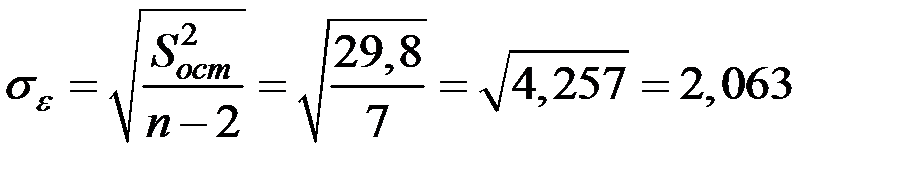 .
.
Пример 5.5. По семи предприятиям лёгкой промышленности региона получена информация, характеризующая зависимость объёма выпуска продукции (Y, млн. руб.) от объёма капиталовложений (X, млн. руб.):
Предприятие 
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
Выпуск 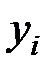
| 152 | 148 | 146 | 134 | 137 | 136 | 134 |
Капвложения 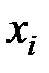
| 86 | 94 | 100 | 96 | 93 | 104 | 122 |
Для характеристики связи объёма выпуска продукции от объёма капиталовложений построить следующие модели: линейную, степенную, показательную, гиперболическую. Оценить качество каждой модели, определив индекс корреляции, среднюю относительную ошибку, коэффициент детерминации, F–критерий Фишера.
Решение. Имеем 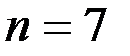 – количество наблюдений,
– количество наблюдений, 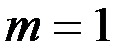 – количество независимых показателей.
– количество независимых показателей.
1. Уравнение линейной регрессии имеет вид:
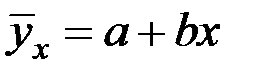 .
.
Рассчитаем основные средние величины показателей.
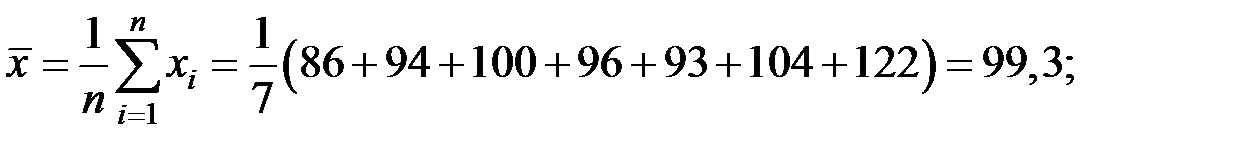
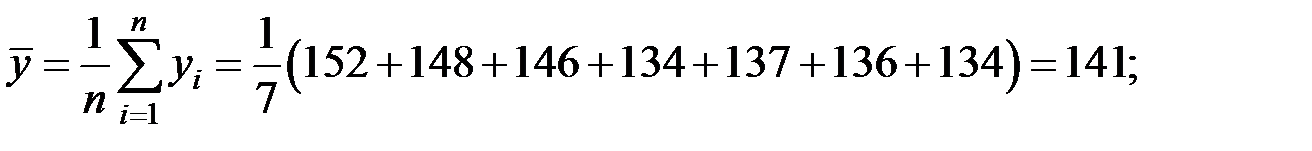
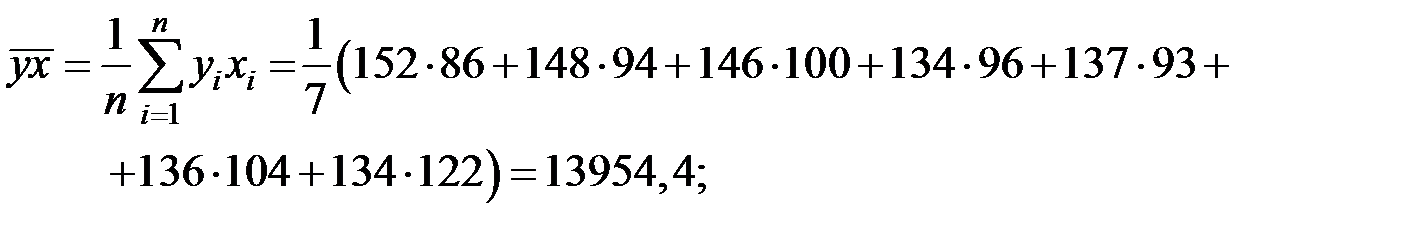
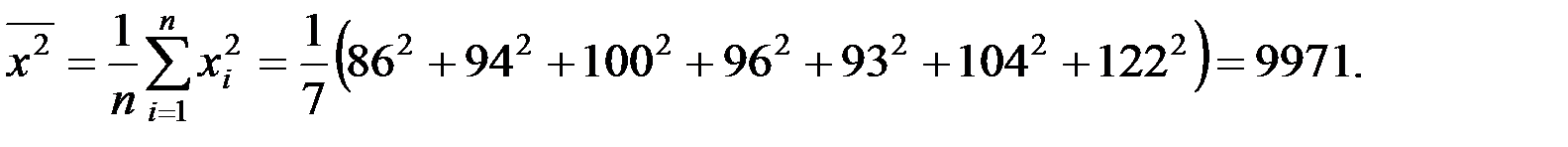
Значение параметров 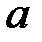 и
и 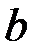 линейной модели определим, используя вычисленные средние значения по данным исходной таблицы.
линейной модели определим, используя вычисленные средние значения по данным исходной таблицы.
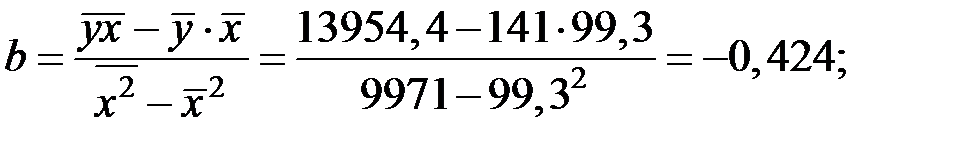
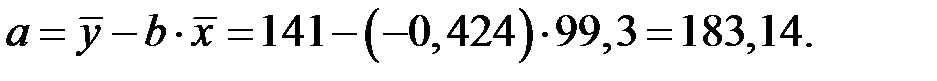
Получаем уравнение линейной регрессии:
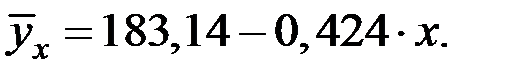
Это означает, что предприятие работает не эффективно.
При увеличении капиталовложений на 1 млн. руб. объём выпускаемой продукции уменьшится на 424 тыс. руб.
Возможно, это связано с реконструкцией предприятия, когда основное внимание уделяется техническому и технологическому переоборудованию производства, а не максимальному выпуску продукции в рассматриваемый период времени.
Определим линейный коэффициент корреляции по формуле: 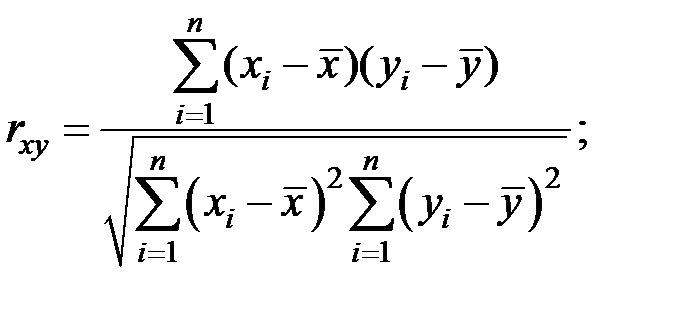
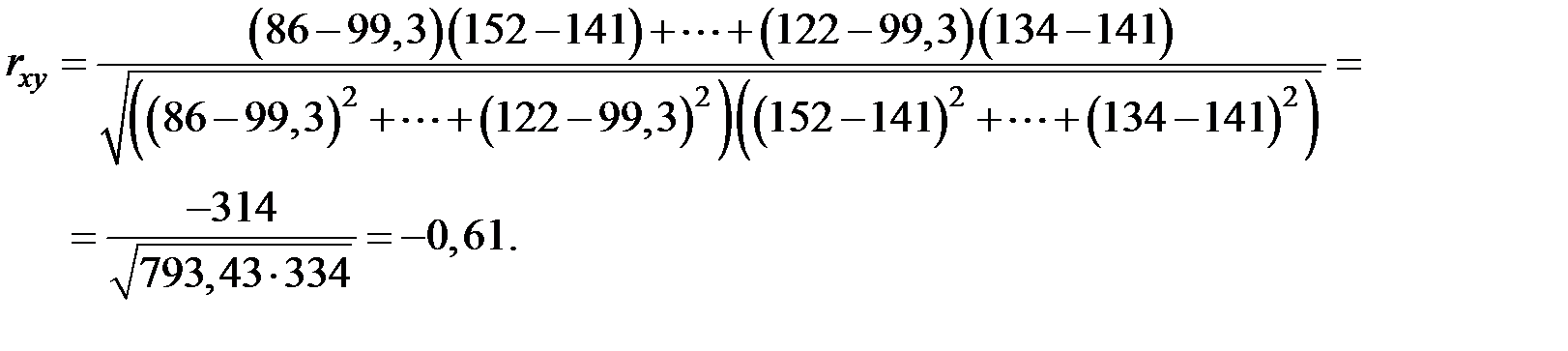 Можно сказать, что связь между объёмом капиталовложений и объёмом выпуска продукции не очень сильная и обратно–пропорциональная.
Можно сказать, что связь между объёмом капиталовложений и объёмом выпуска продукции не очень сильная и обратно–пропорциональная.
Рассчитаем коэффициент детерминации:
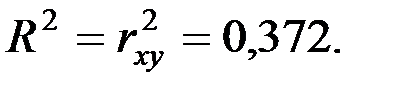
Вариация объёма выпуска продукции на 37,2% объясняется вариацией фактора объёма капиталовложений.
Оценку значимости уравнения регрессии ( 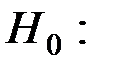 уравнение не значимо) проведём с помощью F–критерия Фишера.
уравнение не значимо) проведём с помощью F–критерия Фишера.
Вычислим наблюдаемое значение критерия:
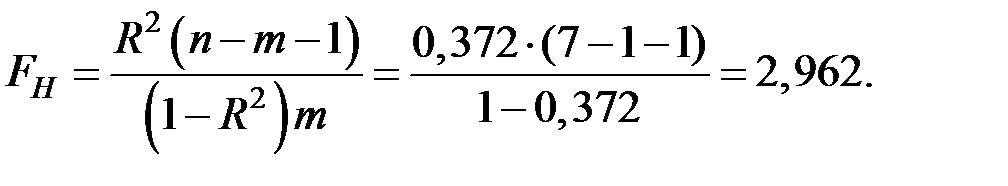
По таблице 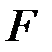 – распределения найдём критическую точку.
– распределения найдём критическую точку.
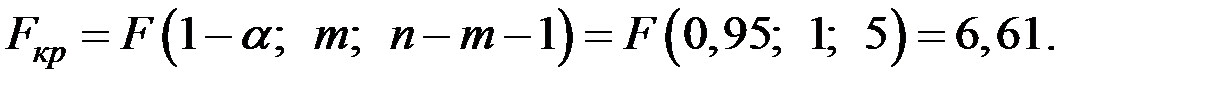
Так как 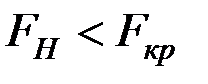 , то нет оснований отвергать гипотезу
, то нет оснований отвергать гипотезу 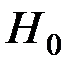 , т.е. уравнение регрессии не значимо при уровне значимости
, т.е. уравнение регрессии не значимо при уровне значимости 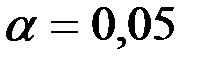 .
.
Для построения значимого линейного уравнения необходимы дополнительные данные или поиск нелинейной зависимости межу исследуемыми показателями.
Определим среднюю относительную ошибку:
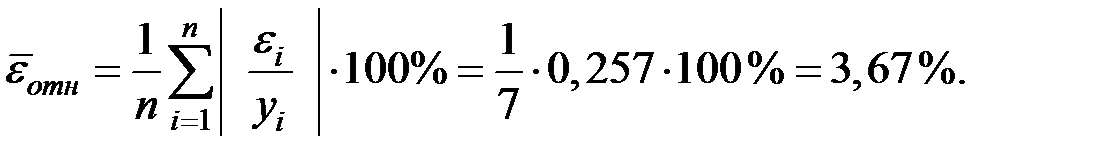
Промежуточные расчёты сведены в таблицу с используемой анализируемой моделью регрессии
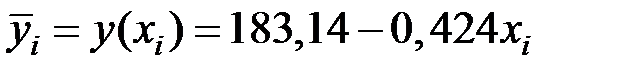 :
:
Предприятие 
| 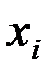
| 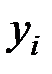
| 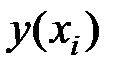
| 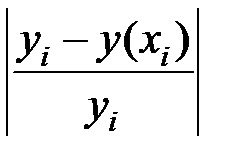
|
| 1 | 86 | 152 | 146,676 | 0,035 |
| 2 | 94 | 148 | 143,284 | 0,032 |
| 3 | 100 | 146 | 140,740 | 0,036 |
| 4 | 96 | 134 | 142,436 | 0,063 |
| 5 | 93 | 137 | 143,708 | 0,049 |
| 6 | 104 | 136 | 139,044 | 0,022 |
| 7 | 122 | 134 | 131,412 | 0,019 |
| Итого: | 0,257 |
В среднем расчётные значения объёма выпуска продукции для линейной модели отличаются от фактических значений на 3,67 %.
2. Уравнение степенной модели имеет вид:
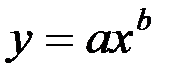 .
.
Для построения этой модели целесообразно (необходимо) произвести линеаризацию переменных.
Для этого произведём десятичное логарифмирование обеих частей уравнения:
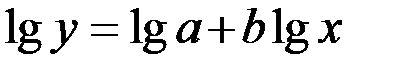 .
.
Обозначим 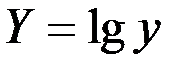 ,
, 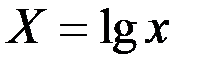 ,
, 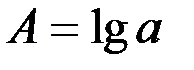 .
.
Тогда уравнение примет линейный вид:
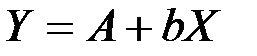 .
.
Промежуточные расчёты для получения линеаризованной модели регрессии сведены в таблицу:
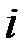
| 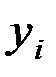
| 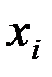
| 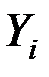
| 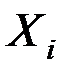
| 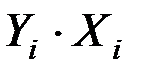
| 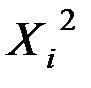
|
| 1 | 152 | 86 | 2,182 | 1,935 | 4,221 | 3,742 |
| 2 | 148 | 94 | 2,170 | 1,973 | 4,282 | 3,893 |
| 3 | 146 | 100 | 2,164 | 2,000 | 4,329 | 4,000 |
| 4 | 134 | 96 | 2,127 | 1,982 | 4,217 | 3,929 |
| 5 | 137 | 93 | 2,137 | 1,969 | 4,206 | 3,875 |
| 6 | 136 | 104 | 2,134 | 2,017 | 4,303 | 4,068 |
| 7 | 134 | 122 | 2,127 | 2,086 | 4,438 | 4,353 |
| Итого | 987 | 695 | 15,041 | 13,962 | 29,996 | 27,861 |
| Ср.знач. | 141 | 99,3 | 2,149 | 1,995 | 4,285 | 3,980 |
Рассчитаем параметры уравнения, используя данные таблицы:
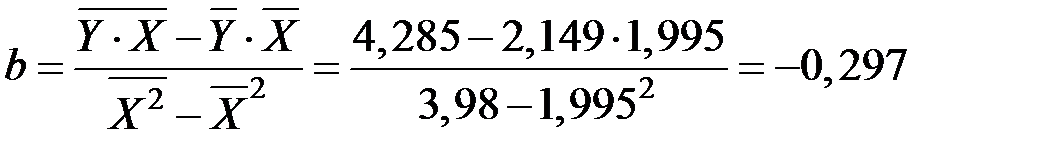 ;
; 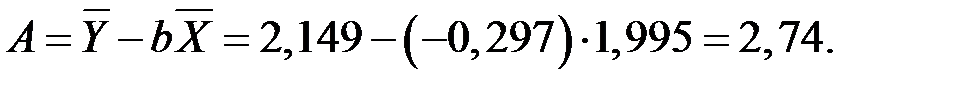
Уравнение линейной регрессии будет иметь вид:
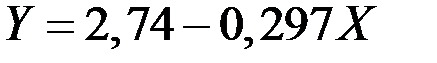 .
.
Перейдём к исходным переменным 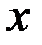 и
и 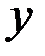 , выполнив потенцирование данного уравнения:
, выполнив потенцирование данного уравнения:
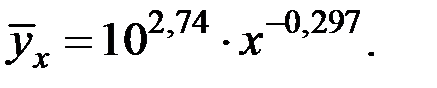
Получим уравнение модели регрессии в виде:
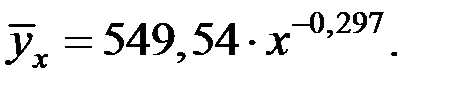
Для оценки качества модели промежуточные расчёты сведём в следующую таблицу:
| Предприятие | 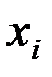
| 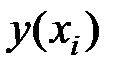
| 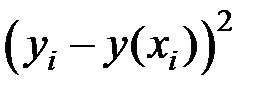
| 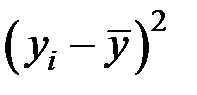
| 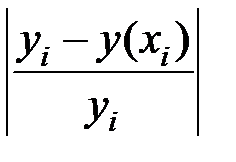
|
| 1 | 86 | 146,370 | 31,692 | 121 | 0,037 |
| 2 | 94 | 142,554 | 29,656 | 49 | 0,037 |
| 3 | 100 | 139,959 | 36,500 | 25 | 0,041 |
| 4 | 96 | 141,666 | 58,763 | 49 | 0,057 |
| 5 | 93 | 143,008 | 36,094 | 16 | 0,044 |
| 6 | 104 | 138,338 | 5,465 | 25 | 0,017 |
| 7 | 122 | 131,932 | 4,276 | 49 | 0,015 |
| Итого | 202,446 | 334 | 0,249 |
Определим индекс корреляции:
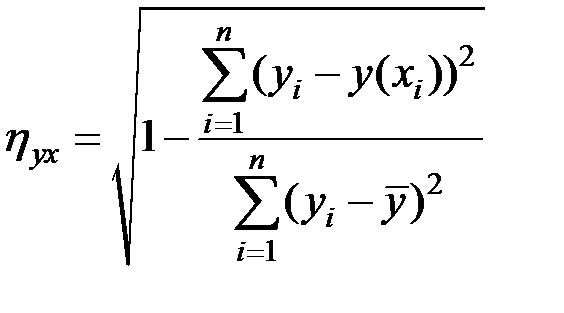 ,
,
где 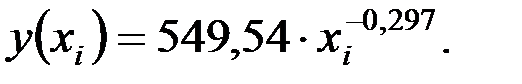
Тогда, используя данные таблицы, получим:
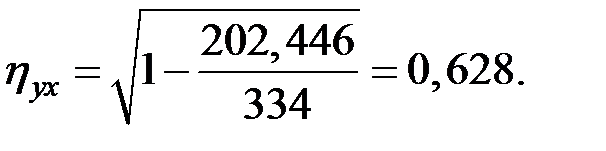
Связь между показателями не очень сильная.
Коэффициент детерминации 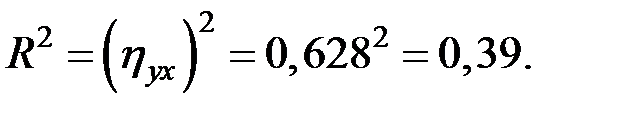
Вариация результата Y (объёма выпуска продукции) по степенной модели на 39% объясняется вариацией фактора X (объёма капвложений).
Оценку значимости уравнения регрессии ( 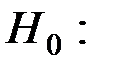 уравнение не значимо) проведём с помощью F–критерия Фишера.
уравнение не значимо) проведём с помощью F–критерия Фишера.
Вычислим наблюдаемое значение критерия:
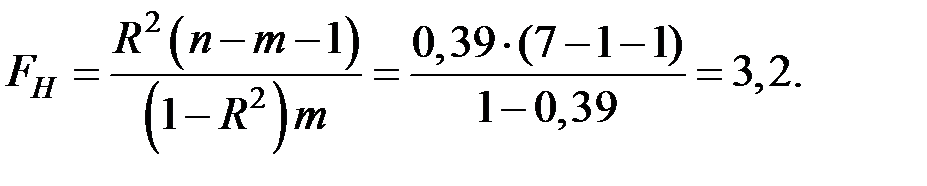
При этом 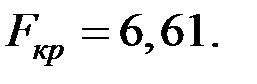
Так как 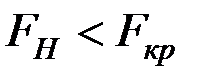 , то нет оснований отвергать гипотезу
, то нет оснований отвергать гипотезу 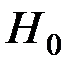 , т.е. уравнение регрессии не значимо при уровне значимости
, т.е. уравнение регрессии не значимо при уровне значимости 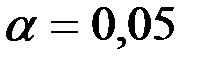 .
.
Определим среднюю относительную ошибку:
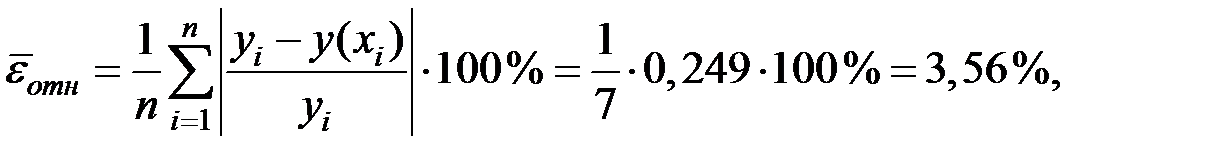
где 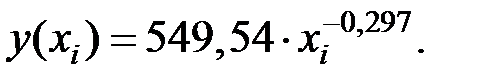
В среднем расчётные значения результирующего показателя для степенной модели отличаются от фактических значений на 3,56 %.
3. Уравнение показательной модели(зависимости): 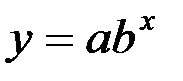 .
.
Для построения этой модели необходимо произвести линеаризацию переменных. Для этого осуществим логарифмирование обеих частей уравнения: 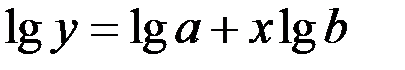 .
.
Обозначим: 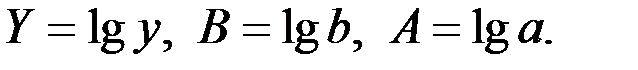
Получим линейное уравнение регрессии: 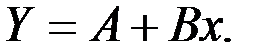
Промежуточные расчёты для получения линеаризованной модели регрессии сведены в таблицу:
Предприятие 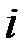
| 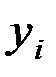
| 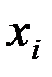
| 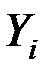
| 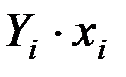
| 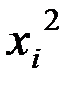
|
| 1 | 152 | 86,0 | 2,182 | 187,639 | 7396 |
| 2 | 148 | 94,0 | 2,170 | 204,005 | 8836 |
| 3 | 146 | 100,0 | 2,164 | 216,435 | 10000 |
| 4 | 134 | 96,0 | 2,127 | 204,202 | 9216 |
| 5 | 137 | 93,0 | 2,137 | 198,715 | 8649 |
| 6 | 136 | 104,0 | 2,134 | 221,888 | 10816 |
| 7 | 134 | 122,0 | 2,127 | 259,507 | 14884 |
| Итого | 987 | 695,0 | 15,041 | 1492,390 | 69797 |
| Средн. знач. | 141 | 99,3 | 2,149 | 213,200 | 9971 |
Рассчитаем параметры уравнения, используя данные таблицы:
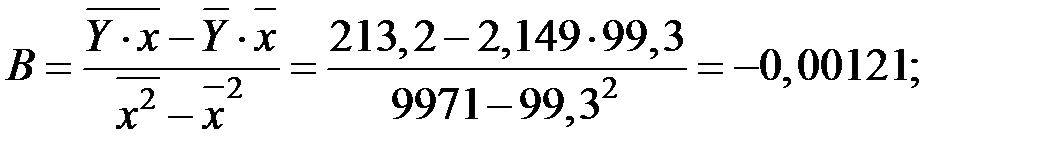
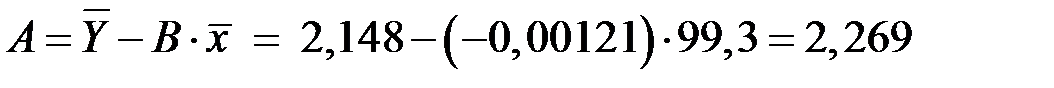 .
.
Линейное уравнение будет иметь вид:
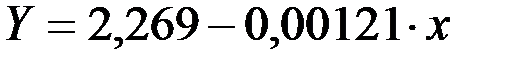 .
.
Перейдём к исходным переменным, выполнив потенцирование данного уравнения:
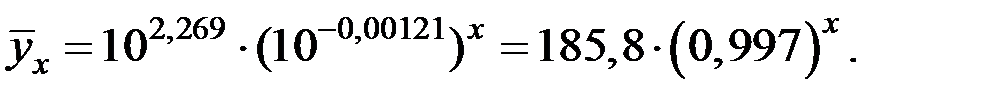
Определим индекс корреляции:
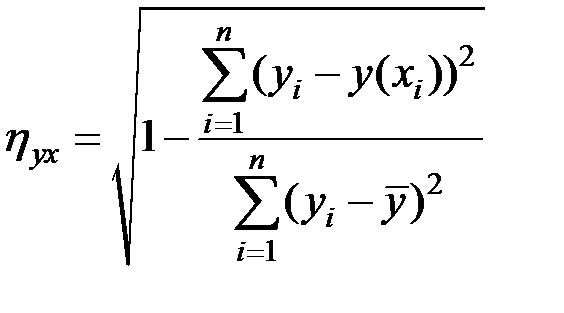 ,
,
где
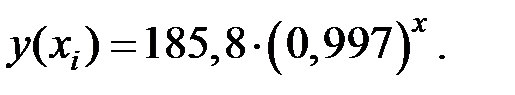
Для оценки качества модели расчёты сведём в таблицу:
Предприятие 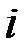
| 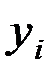
| 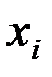
| 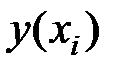
| 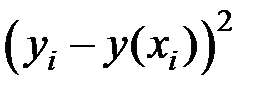
| 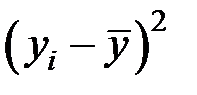
| 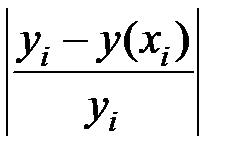
|
| 1 | 152 | 86 | 143,184 | 77,728 | 121 | 0,056 |
| 2 | 148 | 94 | 139,783 | 67,518 | 49 | 0,054 |
| 3 | 146 | 100 | 137,286 | 75,938 | 25 | 0,058 |
| 4 | 134 | 96 | 138,946 | 24,459 | 49 | 0,039 |
| 5 | 137 | 93 | 140,204 | 10,264 | 16 | 0,026 |
| 6 | 136 | 104 | 135,646 | 0,126 | 25 | 0,001 |
| 7 | 134 | 122 | 128,505 | 30,198 | 49 | 0,039 |
| Итого | 286,231 | 334 | 0,271 |
Тогда, используя данные таблицы, получим:
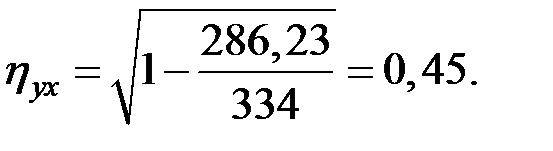
Связь между показателями слабая.
Коэффициент детерминации
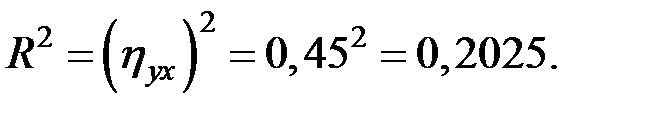
Вариация результата объёма выпуска продукции на 20,25% объясняется вариацией объёма капиталовложений.
Вычислим наблюдаемое значение F–критерия Фишера для модели:
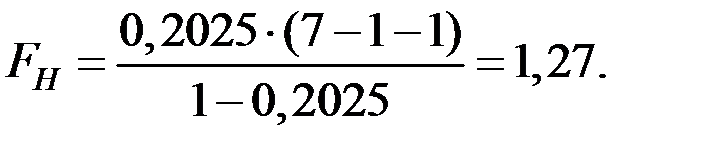
При этом 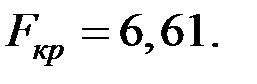
Так как 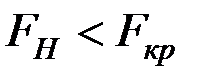 , то нет оснований отвергать гипотезу
, то нет оснований отвергать гипотезу 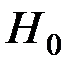 , т.е. уравнение регрессии не значимо при уровне значимости
, т.е. уравнение регрессии не значимо при уровне значимости 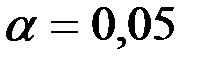 .
.
Определим среднюю относительную ошибку:
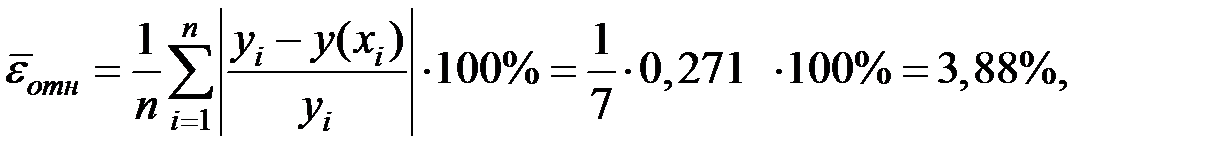
где
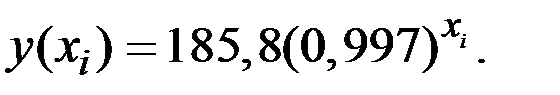
В среднем расчётные значения результирующего показателя для степенной модели отличаются от фактических значений на 3,88%.
4. Уравнение гиперболической функции: 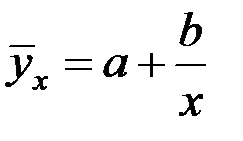 .
.
Произведём линеаризацию модели путём замены 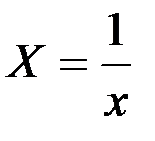 .
.
В результате получим линейное уравнение регрессии: 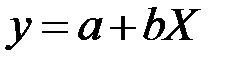 .
.
Промежуточные расчёты для получения линеаризованной модели регрессии сведены в таблицу:
Предприятие 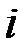
| 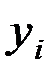
| 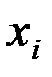
| 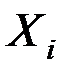
| 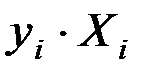
| 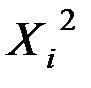
|
| 1 | 152 | 86,0 | 0,012 | 1,767 | 0,0001 |
| 2 | 148 | 94,0 | 0,011 | 1,575 | 0,0001 |
| 3 | 146 | 100,0 | 0,010 | 1,460 | 0,0001 |
| 4 | 134 | 96,0 | 0,010 | 1,396 | 0,0001 |
| 5 | 137 | 93,0 | 0,011 | 1,473 | 0,0001 |
| 6 | 136 | 104,0 | 0,010 | 1,308 | 0,0001 |
| 7 | 134 | 122,0 | 0,008 | 1,098 | 0,0001 |
| Итого | 987 | 695,0 | 0,071 | 10,077 | 0,0007 |
| Средн. знач. | 141 | 99,3 | 0,010 | 1,440 | 0,0001 |
Рассчитаем параметры модели по данным таблицы.
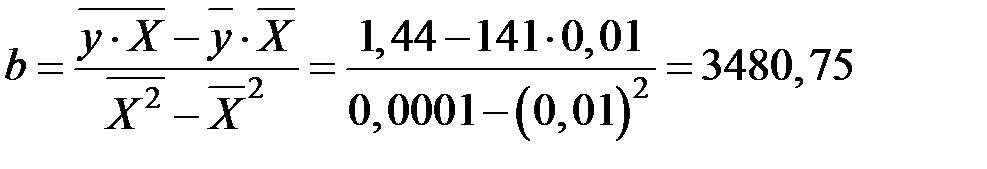 .
.
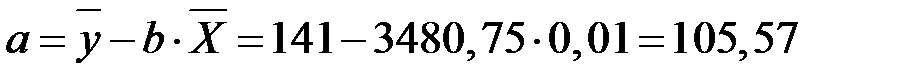 .
.
Получим следующее уравнение гиперболической модели:
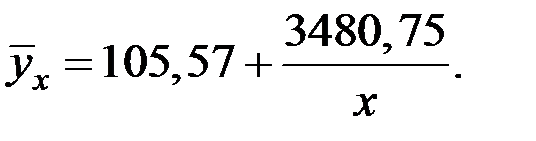
Для оценки качества модели расчёты сведём в таблицу:
| Предприятие | 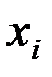
| 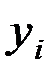
| 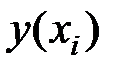
| 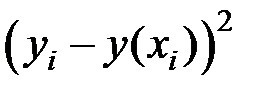
| 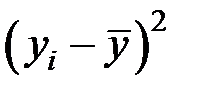
|
| 1 | 86 | 152 | 142,489 | 35,476 | 121 |
| 2 | 94 | 148 | 139,105 | 29,168 | 49 |
| 3 | 100 | 146 | 136,619 | 31,613 | 25 |
| 4 | 96 | 134 | 138,271 | 61,275 | 49 |
| 5 | 93 | 137 | 139,523 | 35,969 | 16 |
| 6 | 104 | 136 | 134,987 | 9,234 | 25 |
| 7 | 122 | 134 | 127,881 | 0,010 | 49 |
| Итого | 202,744 | 334 |
Определим индекс корреляции:
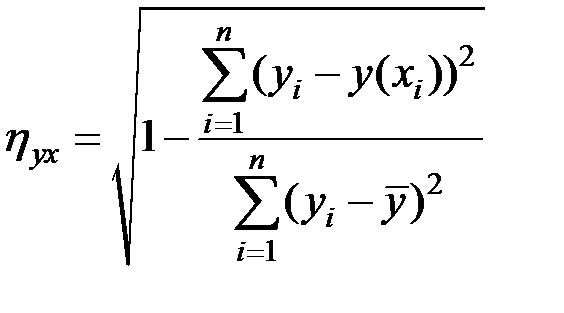 ,
,
где
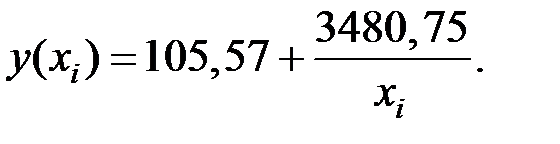
Тогда индекс корреляции будет равен величине
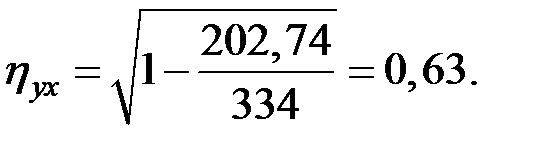
Связь между показателями и в этой модели слабая.
Коэффициент детерминации незначителен:
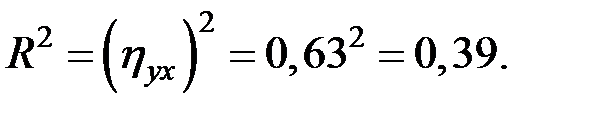
Вычислим наблюдаемое значение F–критерия Фишера:
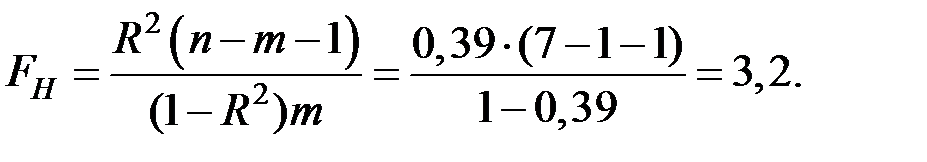
При этом
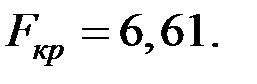
И эта модель регрессии не значима при уровне значимости 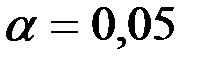 .
.
Определим среднюю относительную ошибку:
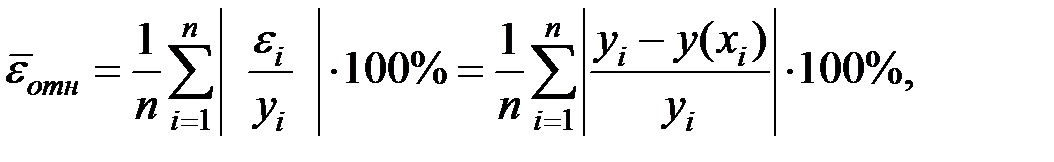
где
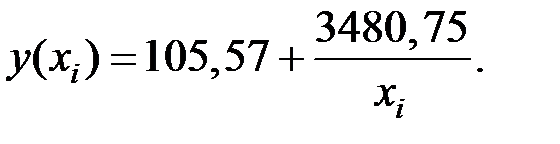
Тогда получим:
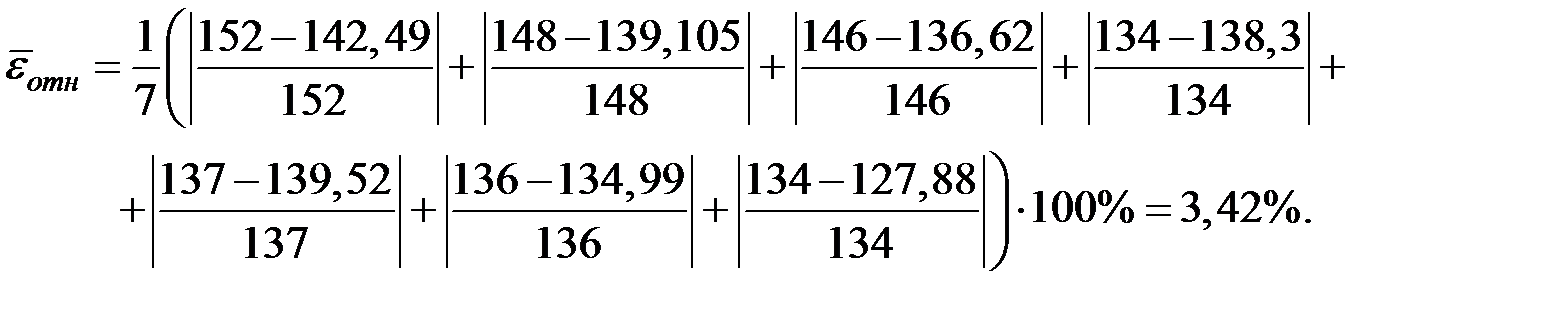
В среднем расчётные значения результирующего показателя для степенной модели отличаются от фактических значений на 3,42%.
Для экономических задач эта величина (модель) считается достаточно точной, но модель не значима, так как мало наблюдений.
Следует увеличить объём исходных данных.
.
Множественная регрессия
B множественном (многомерном) регрессионном анализе пытаются найти зависимость одной зависимой переменной от нескольких независимых: 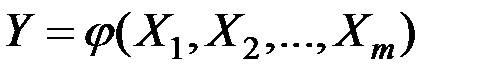 .
.
Связь между переменной 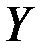 и m независимыми факторами можно охарактеризовать функцией регрессии
и m независимыми факторами можно охарактеризовать функцией регрессии 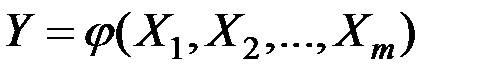 , которая показывает, каково будет в среднем значение переменной
, которая показывает, каково будет в среднем значение переменной 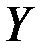 , если переменные
, если переменные 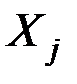
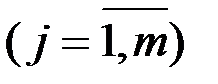 примут конкретные значения.
примут конкретные значения.
Практика построения многофакторных моделей показывает, что реально существующие в экономике (на практике) зависимости можно описать, используя следующие типы моделей:
1) линейная 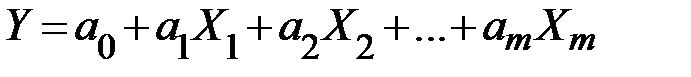 ;
;
2) степенная 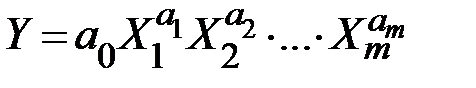 ;
;
3) экспоненциальная 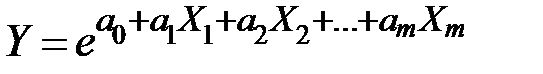 ;
;
4) параболическая 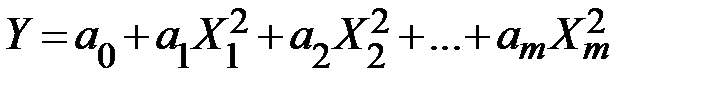 ;
;
5) гиперболическая 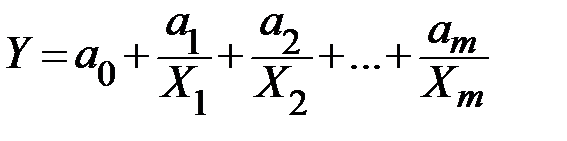 .
.
Основное значение имеют линейные модели (относительно параметров регрессии) в силу своей простоты. Нелинейные формы зависимости часто преобразуются к линейным путём линеаризации.
Наиболее приемлемым способом определения вида уравнения регрессии является метод перебора различных уравнений регрессии.
Наилучшие значения параметров регрессии 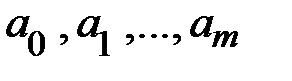 определяются методом наименьших квадратов.
определяются методом наименьших квадратов.
Коэффициенты регрессии находятся по критерию:
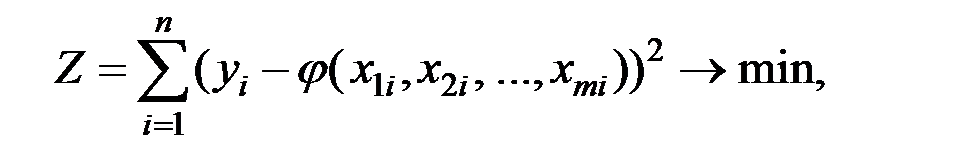
где 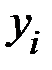 – значение результативного фактора (зависимой переменной)
– значение результативного фактора (зависимой переменной) 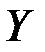 в
в 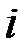 –ом наблюдении;
–ом наблюдении; 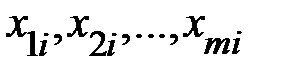 – значения факторов
– значения факторов 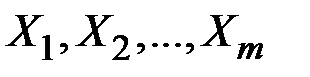 в
в 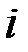 –ом наблюдении;
–ом наблюдении; 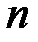 – количество наблюдений.
– количество наблюдений.
Реализация этого критерия приводит к системе уравнений
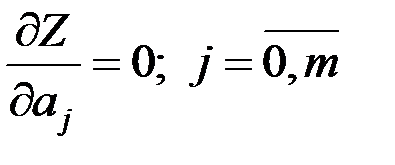
из которой определяются параметры 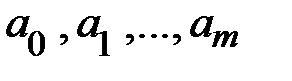 .
.
Дата: 2019-03-05, просмотров: 980.