Использование методов типа максимального правдоподобия имеет тот недостаток, что объем выборки определяется заранее, и уже после определяется достигнутая точность, т.е. ошибки первого и второго рода.
Это обстоятельство учтено в предложенном А.Вальдом методе последовательного анализа.
Сущность метода последовательного анализа состоит в следующем.
Все множество значений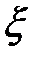 
делится не на две, а на три области:
1) область допустимых значений R1,
2) критическую область R2,
3) некоторую промежуточную область R3.
Значения 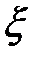вычисляются последовательно после каждого наблюдения.
Если после n–го (n = 1, 2, ...) наблюдения получаем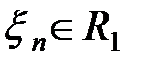 
, то гипотеза H0 принимается, и эксперимент на этом заканчивается.
Если 
, то гипотеза H0 отвергается, и эксперимент также прекращается.
Если же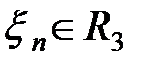 
, то никакого решения относительно правильности гипотезы не принимается, и эксперимент продолжается далее (т.е. делается (n+1)–е наблюдение и оценивается принадлежность 
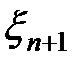областям R1, R2 и R3).
Вероятности ошибок первого и второго рода в этом случае, соответственно, будут определяться соотношениями
;
.
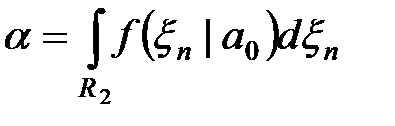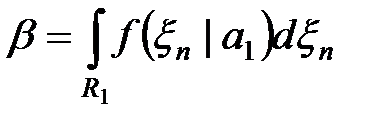Из существа метода ясно, что вероятности ошибок при фиксированных областях R1 и R2 зависят от числа проведённых наблюдений.
Так как рассеивание 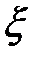убывает с ростом объёма выборки n, то 
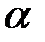и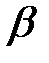 
, естественно, уменьшаются.
Так как вероятности ошибок первого и второго рода однозначно связаны с областями R1 и R2, то разумно поступить следующим образом: зафиксировать допустимые величины вероятностей ошибок первого и второго рода и для каждого n–го наблюдения определить соответствующие им области R1n и R2n (следует заметить, что в общем случае задача отыскания границ этих областей весьма сложна).
На рис. 2.4 даны графическое представление допустимой, критической и промежуточной областей, а также вероятностей ошибок первого и второго рода.
|
|
|
|
|
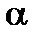
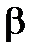
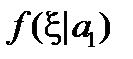
| R1 |
| R3 |
| R2 |
Рис. 2.4. Графическое представление областей для оценки гипотезы
Применение метода последовательного анализа позволяет в среднем существенно сократить число наблюдений над случайной величиной (объём выборки) при сохранении той же точности решения о правдоподобии гипотезы.
Контрольные вопросы к главе 2
1. Какие этапы выделяются при проверке гипотез по статистическим данным?
2. Что такое уровень значимости при проверке гипотез?
3. Поясните методику использования Критерия Пирсона.
4. Поясните методику получения закона распределения случайной величины по статистическим данным.
5. Поясните методику использования метода максимального правдоподобия при проверке гипотез.
6. Поясните смысл ошибок первого и второго рода.
7. Как проверяются гипотезы по статистическим данным?
8. Что такое ошибки первого и второго рода при проверке гипотез по статистическим данным?
9. Приведите примеры некоторых гипотез и критериев их проверки.
10. Что такое метод последовательного анализа при проверке гипотез по статистическим данным?
11. Поясните различие параметрических и непараметрических критериев проверки гипотез.
12. Что такое мощность статистического критерия проверки гипотез?
13. Как проверить значимость расхождений двух дисперсий нормальных генеральных совокупностей?
14. Как определяются критические точки критериев?
15. Как проверить значимость расхождений двух средних значений нормальных генеральных совокупностей?
16. Как уровень значимости связан с доверительной вероятностью?
ЗАДАНИЕ ДЛЯ КОНТРОЛЬНОЙ РАБОТЫ № 2
ЗАДАНИЕ 2.1. По имеющимся статистическим данным и результатам расчётов, выполненных в заданиях 1.1 и 1.2, проверить гипотезы:
1) о непротиворечивости данных полученному закону;
2) о равенстве выборочных параметров статистического распределения (математического ожидания, дисперсии, среднего квадратического отклонения) с гипотетическими (гипотетические параметры принять «на глазок», исходя из физических свойств распределения, используя правило трёх сигм и «центра тяжести»).
Уровень значимости принимать в пределах 0,01 – 0,2.
Проанализировать полученные результаты.
Дата: 2019-03-05, просмотров: 377.
