Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Понятие эластичности функции нескольких переменных вводится аналогично понятию эластичности функции одной переменной.

Пусть, например, 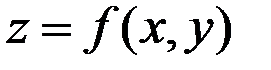 – функция двух переменных.

Её частные приращения:

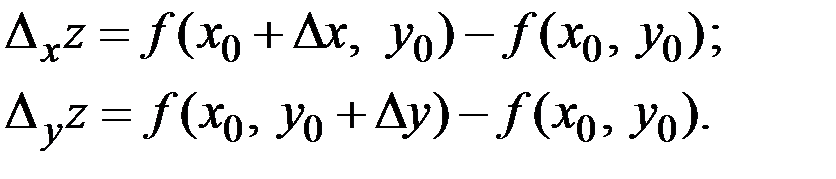
Эластичностью функции 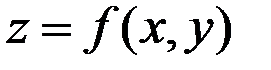 в точке  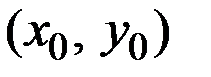пo х называется предел следующего вида

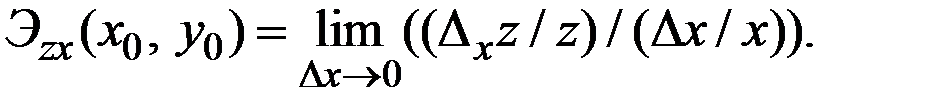
Эластичностью функции 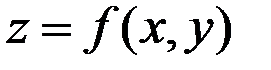 пo у в той же точке называется предел

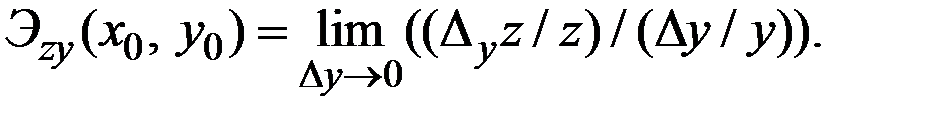
Из определения эластичности вытекают следующие формулы:

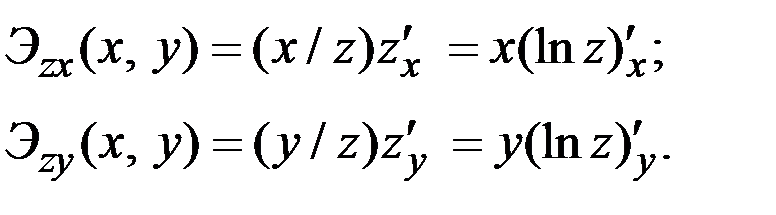
Прим ер 3.13. Найти коэффициенты эластичности по х и по у функции 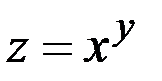 в точке (2; 3).

Решение. Согласно полученным выше формулам имеем

 

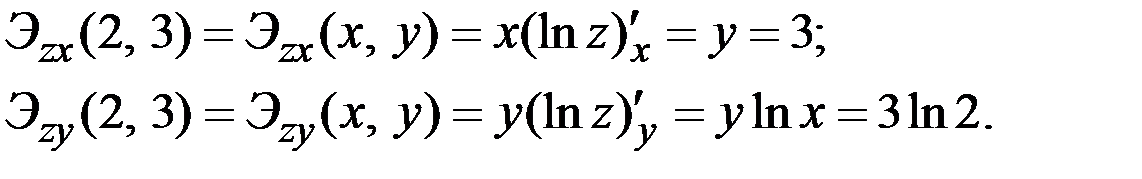
Рассмотренные формулы полностью аналогичны формулам, которые использовались при анализе свойств 1 – 3 эластичности в одномерном случае. Поэтому первые три свойства эластичности справедливы и в случае функции нескольких переменных.

Третье и четвёртое свойства также сохраняются, но формы их записи становятся сложнее.

Остановимся подробнее на этих свойствах.

Свойство 4: Для функций

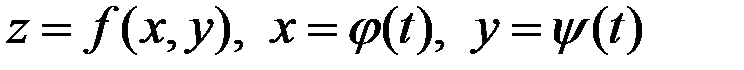
эластичность z пo t в точке 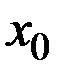, находится по формуле

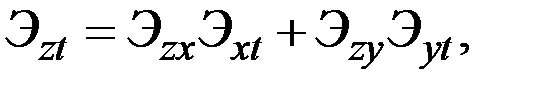
где 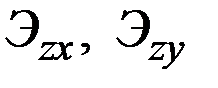 – эластичности z пo х и у в точке ( ,

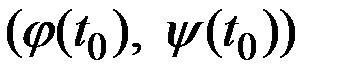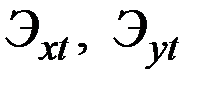 – эластичности х и у по t в точке .

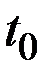Пара функций 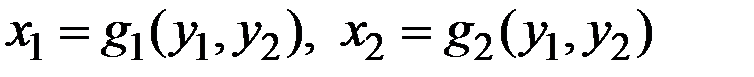, называется обратной для пары функций 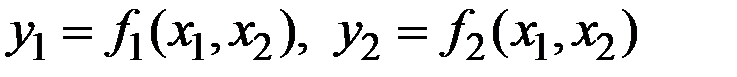, заданных на множестве 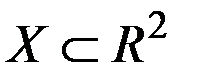, если для любой точки 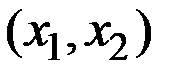из Х выполняются равенства:

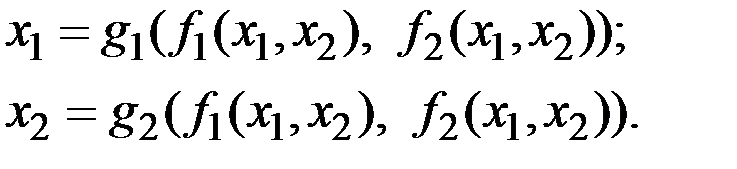
Пример 3.14 . Найти пару обратных функций для функций

,

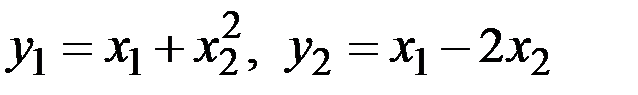заданных в .

Решение. Из равенства 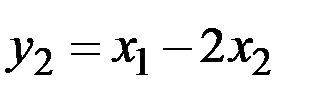 следует, что

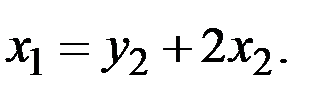
Поэтому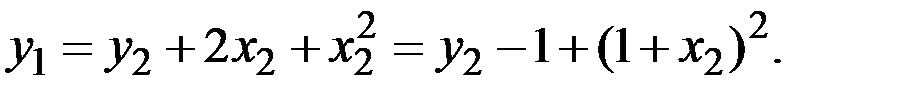

Находим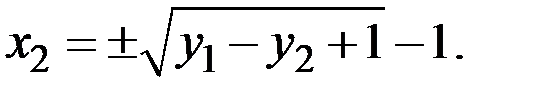

Учитывая, что 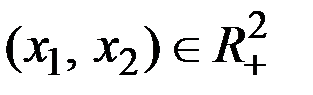 , имеем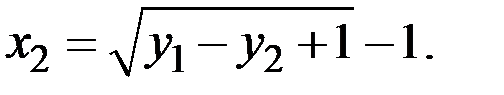

Следовательно,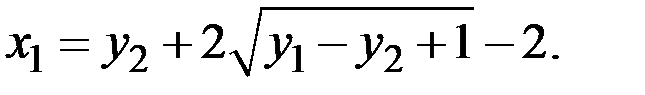

 

Для любой пары функций 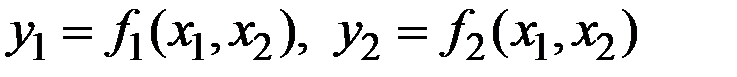 имеем 4 коэффициента эластичности ).

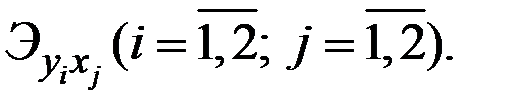Записав их в виде таблицы, получим матрицу размера 2х2:

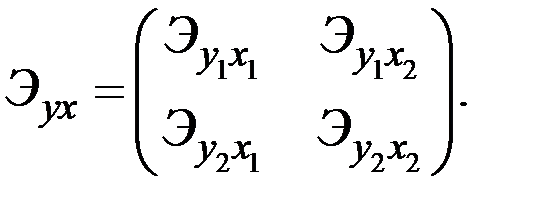
Элементы этой матрицы, расположенные вне главной диагонали, называются перекрёстными коэффициентами эластичности.

Свойство 5. Пусть 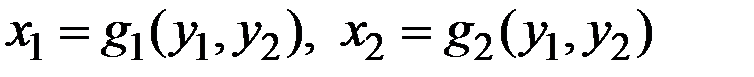 – пара обратных функций для функций 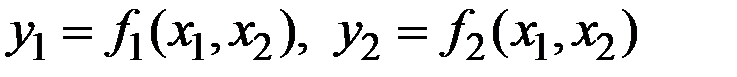. Тогда матрица коэффициентов эластичности  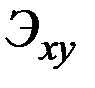является обратной к матрице .

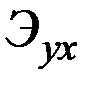Пример 3.15. По данным выборочного обследования бюджетов домашних хозяйств рассчитать коэффициенты эластичности потребления продуктов питания:

Показатель

Год

Базисный Отчётный Потребление на одного члена домохозяйства в год, кг.: 1) хлебопродуктов (Y₁) 2) молока и молочных продуктов (Y₂) Среднедушевые доходы на домохозяйство за год в сопоставимых ценах, руб. (Х)   98 296   3400   104 274   3790

Решение. Рассчитаем коэффициент эластичности потребления продуктов от дохода по формуле

,

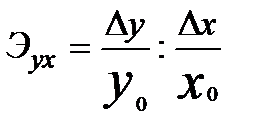где 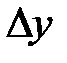– изменение уровня потребления в отчётном периоде по сравнению с базисным, т.е. ;

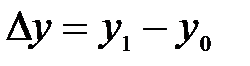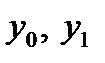 – уровни потребления в базовом и отчётном периодах;

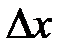 – изменение среднедушевого дохода за данный период, т.е.

;

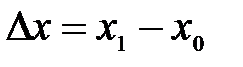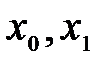 – среднедушевой доход в базовом и отчётном периодах.

Представим расчётные показатели в следующем виде:

Показатель	Абсолютный прирост	Темп роста, %	Темп прироста, %
Потребление в среднем на одного члена домохозяйства в год, кг.: 1) хлебопродуктов 2) молока и молочных продуктов Среднедушевые доходы на домохозяйство за год в сопоставимых ценах, руб.	6 – 22   390	106,12 92,57   111,47	6,12 – 7,43   11,47

Коэффициент эластичности потребления хлебопродуктов равен

.

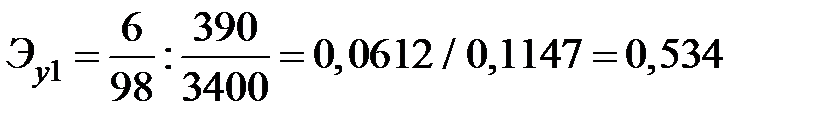Эластичность потребления молока и молочных продуктов равен

.

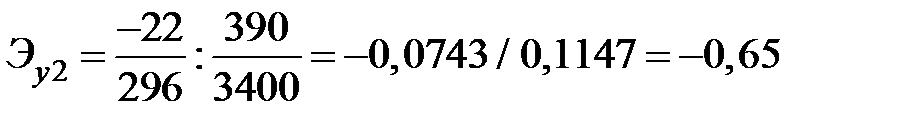Следовательно, потребление хлебопродуктов составило 0,53% на 1% прироста дохода, а по молоку и молочным продуктам наблюдалось снижение потребления, равное 0,65% на 1% прироста доходов.