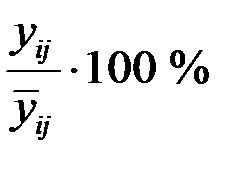Пример 3.16. Реализация картофеля на рынках города за три года характеризуется следующими данными, тонн:
|
Год | Месяц | |||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
| 2012 2013 2014 | 70 71 63 | 71 85 60 | 82 84 59 | 190 308 281 | 280 383 384 | 472 443 483 | 295 261 305 | 108 84 129 | 605 630 670 | 610 450 515 | 184 177 185 | 103 168 104 |
Определить индексы сезонности.
Решение. Для исчисления индексов сезонности применяют различные методы, выбор которых зависит от характера общей тенденции ряда динамики.
Если ряд динамики не содержит ярко выраженной тенденции развития, то индексы сезонности исчисляют непосредственно по эмпирическим данным без их предварительного выравнивания.
Для расчёта индексов сезонности необходимо иметь помесячные данные минимум за три года.
Для каждого месяца рассчитывается средний уровень 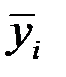 , затем исчисляется среднемесячный уровень для всего анализируемого ряда
, затем исчисляется среднемесячный уровень для всего анализируемого ряда 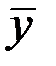 .
.
По этим данным определяется индекс сезонности 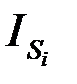 как процентное соотношение средних для каждого месяца к общему среднемесячному уровню ряда:
как процентное соотношение средних для каждого месяца к общему среднемесячному уровню ряда:
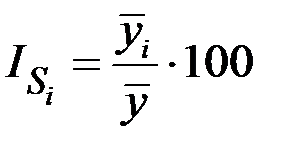 ,
,
где 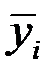 – среднемесячные уровни ряда (по одноимённым месяцам);
– среднемесячные уровни ряда (по одноимённым месяцам);
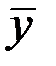 – общий средний уровень ряда (постоянная средняя).
– общий средний уровень ряда (постоянная средняя).
По формуле простой средней арифметической
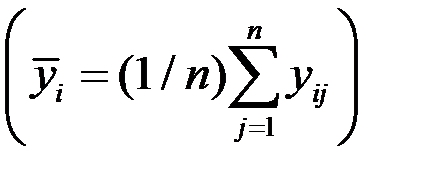 ,
,
определим среднемесячные уровни за три года:
январь:
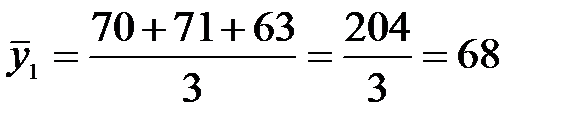 тн.;
тн.;
февраль:
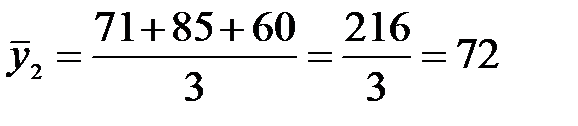 тн. и т.д.
тн. и т.д.
Исчислим общую (постоянную) среднюю:
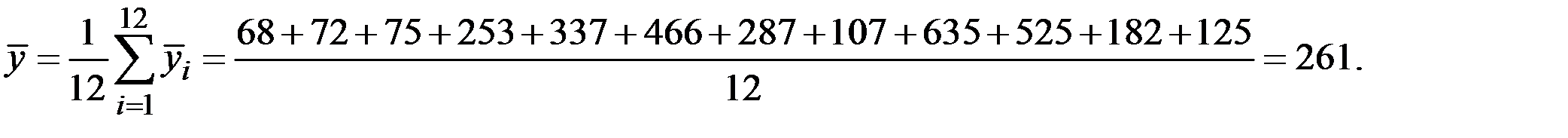
или 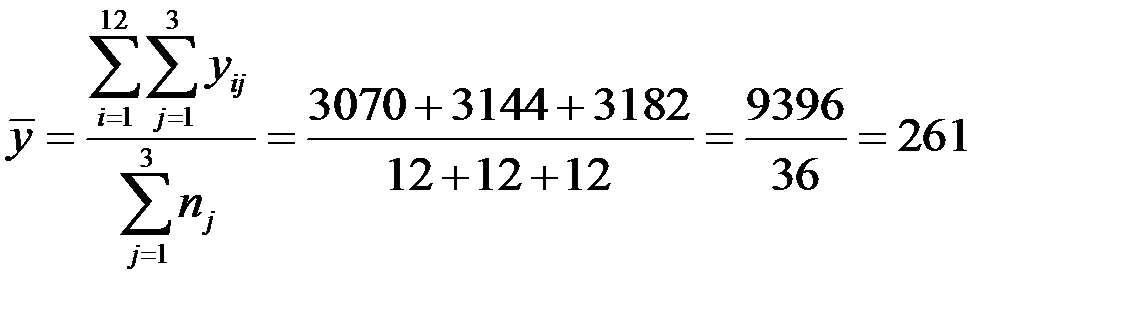 тн.
тн.
Индексы сезонности имеют следующие значения:
январь:
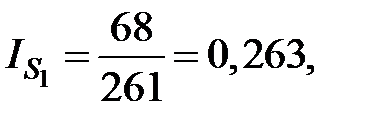 или 26,3%;
или 26,3%;
февраль:
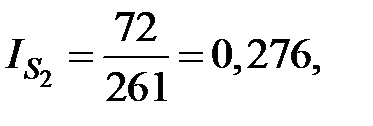 или 27,6%, и т.д. (табл. 3.5).
или 27,6%, и т.д. (табл. 3.5).
Индексы сезонности показывают, что наименьший спрос приходится на январь – февраль, а наибольший – на сентябрь – октябрь.
Для наглядности можно построить график сезонной волны реализации картофеля (рис. 3.2).
Таблица 3.5
Реализация картофеля на рынках города за три года
|
Месяц | Реализация картофеля, тн. | Индексы сезонности
| ||||
| 2012 | 2013 | 2014 | Сумма за три года | Среднемесячная за три года, 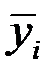
| ||
| Январь Февраль Март Апрель Май Июнь Июль Август Сентябрь Октябрь Ноябрь Декабрь | 70 71 82 190 280 472 295 108 605 610 184 103 | 71 85 84 308 383 443 261 84 630 450 177 168 | 63 60 59 261 348 483 305 129 670 515 185 104 | 204 216 225 759 1011 1398 861 321 1905 1575 546 375 | 68 72 75 253 337 466 287 107 635 525 182 125 | 26,3 27,6 28,7 96,9 129,1 178,5 110,0 41,0 243,3 201,0 69,7 47,9 |
| Итого | 3070 | 3144 | 3182 | 9396 | 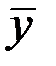 = 261 = 261
| 100,0 |
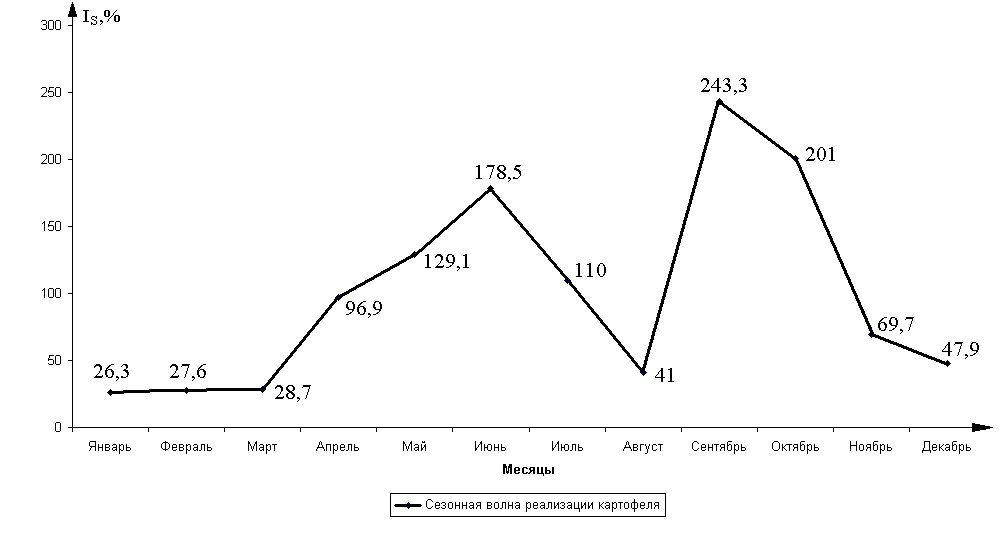
Рис. 3.2. Сезонная волна реализации картофеля
(изменение индексов сезонности по месяцам в среднем за три года)
Пример 3.17. Имеются следующие данные о внутригодовой динамике заготовок сельскохозяйственной продукции области по кварталам за три года:
| Квартал | Заготовлено продукции, тыс. руб. | ||
| Первый год | Второй год | Третий год | |
| 1 2 3 4 | 162 170 177 151 | 159 193 178 168 | 158 225 187 172 |
Определить квартальные индексы сезонности.
Решение. Вычислим квартальные индексы сезонности в рядах динамики с тенденцией развития (с переменной средней).
Когда уровни ряда динамики проявляют тенденцию к росту или снижению, то отклонения от постоянного среднего уровня могут исказить сезонные колебания. В таких случаях физические данные сопоставляются с выравненными. Для расчёта индекса сезонности в таких рядах динамики применяется формула
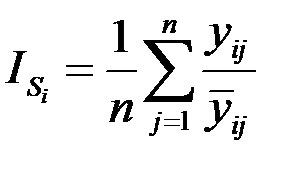 ,
,
где 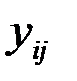 – эмпирические уровни ряда;
– эмпирические уровни ряда; 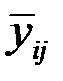 – теоретические уровни ряда;
– теоретические уровни ряда;
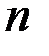 – число периодов (лет).
– число периодов (лет).
Определим теоретические значения 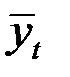 по уравнению
по уравнению 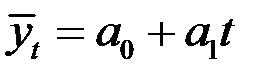 .
.
Для расчёта параметров 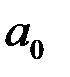 и
и 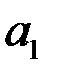 составим табл. 3.6 (подробнее см. главу 5). Вычислим параметры:
составим табл. 3.6 (подробнее см. главу 5). Вычислим параметры:
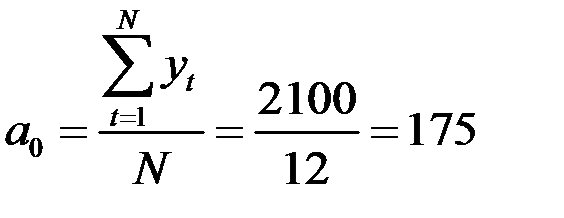 ;
; 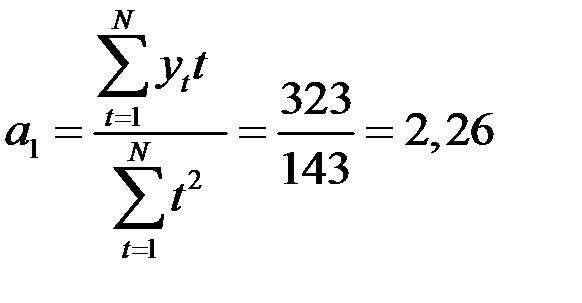 .
.
Следовательно, уравнение имеет вид 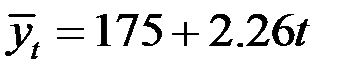 .
.
Подставив в это уравнение значения 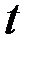 (квартальные), получим следующие выравненные значения ряда.
(квартальные), получим следующие выравненные значения ряда.
Для первого года:
1 квартал: 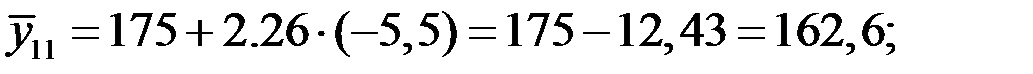
2 квартал: 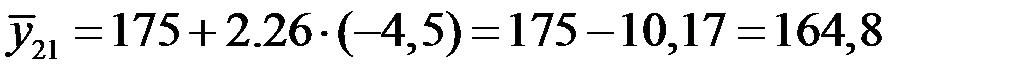 ;
;
3 квартал: 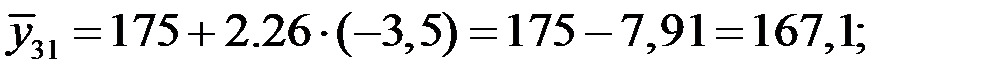 и т.д. (табл. 3.6).
и т.д. (табл. 3.6).
Таблица 3.6
Расчёт параметров линейной модели
| Квартал | Эмпирические уровни ряда 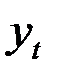
|
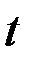
|
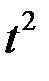
|
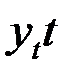
|
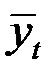
| 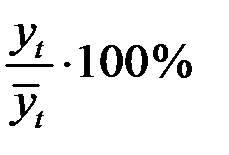
|
| Первый год | ||||||
| 1 2 3 4 | 162 170 177 151 | –5,5 –4,5 –3,5 –2,5 | 30,25 20,35 12,25 6,25 | –891,0 –765,0 –619,5 –377,5 | 162,6 164,8 167,1 169,4 | 99,6 103,2 195,9 89,1 |
| Второй год | ||||||
| 1 2 3 4 | 159 193 178 168 | –1,5 –0,5 0,5 1,5 | 2,25 ,25 ,25 2,25 | –238,5 –96,5 89,0 252,0 | 171,6 173,9 176,6 178,4 | 92,7 111,0 101,1 94,2 |
| Третий год | ||||||
| 1 2 3 4 | 158 225 187 172 | 2,5 3,5 4,5 5,5 | 6,25 12,25 20,25 30,25 | 395,0 787,5 841,5 946,0 | 180,7 182,9 185,2 187,3 | 87,4 123,0 101,0 91,8 |
| Сумма | 2100 | 0 | 143 | 323 | 2100 | |
Найдём для каждого квартала процентные отношения эмпирических уровней ряда 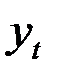 к теоретическим уровням
к теоретическим уровням 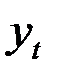 , т.е.
, т.е. 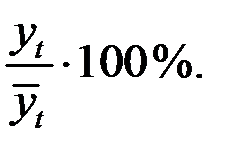
Тогда для первого года:
1 квартал: 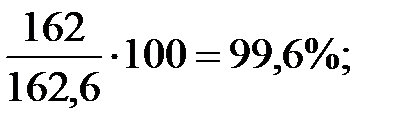

2 квартал: 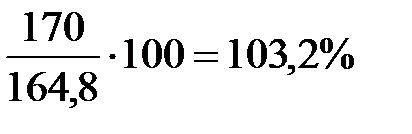 и т.д.
и т.д.
Для третьего года:
4 квартал: 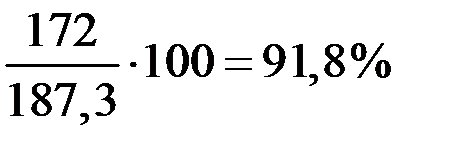 .
.
После этого нужно просуммировать полученные процентные отношения 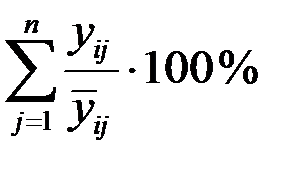 за три года по одноимённым кварталам (табл. 3.7):
за три года по одноимённым кварталам (табл. 3.7):
1 квартал: 99,6 + 92,7 + 87,4 = 279,7;
2 квартал: 103,2 + 111,0 + 123,0 = 337,2 и т.д.
Затем следует исчислить индексы сезонности (табл. 3.7).
Таблица 3.7
Динамика заготовок сельскохозяйственной продукции области
| К в а р т а л |
Эмпирические данные |
Теоретические данные | Эмпирические данные в процентах от теоретических | Сумма процент–ных отношений: (7) + (8) +(9) | Индексы сезонности, % | ||||||
| 1–й год | 2–й год | 3–й год | 1–й год | 2–й год | 3–й год | 1–й год | 2–й год | 3–й год | |||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | |
| 1 2 3 4 | 162 170 177 151 | 159 193 178 168 | 158 225 187 172 | 162,6 164,8 167,1 169,4 | 171,6 173,9 176,1 187,4 | 180,8 182,9 185,2 178,4 | 99,6 103,2 105,9 89,1 | 92,7 111,0 101,1 94,2 | 87,4 123,0 101,0 91,8 | 279,7 337,2 308,0 275,1 | 93,2 112,4 102,7 91,7 |
| Итого | 660 | 698 | 742 | 100,0 | |||||||
Индексы сезонности характеризуют размеры заготовок сельскохозяйственной продукции в зависимости от времени года.
Наибольший удельный вес заготовок сельскохозяйственной продукции приходится на второй квартал.
Чтобы наглядно представить сезонную волну, индексы сезонности обычно наносят на график.
Пример 3.18. Имеются следующие данные о распределении общего объёма денежных доходов населения региона по 20% – ым группам, %:
| Показатель | Базисный год | Отчётный год |
| Денежные доходы – всего | 100 | 100 |
| в т.ч. по 20%–м группам населения: | ||
| Первая (с наименьшими доходами) | 9,8 | 6,5 |
| Вторая | 14,9 | 10,6 |
| Третья | 18,8 | 16,5 |
| Четвертая | 23,8 | 22,5 |
| Пятая (с наибольшими доходами) | 32,7 | 43,9 |
Для каждого года: 1) определить коэффициенты концентрации доходов Джини; 2) построить кривую Лоренца; 3) вычислить индекс коэффициента концентрации доходов Джини.
Решение. Коэффициент концентрации доходов Джини (KG) показывает распределение всей суммы доходов населения между его отдельными группами и определяется по формуле:
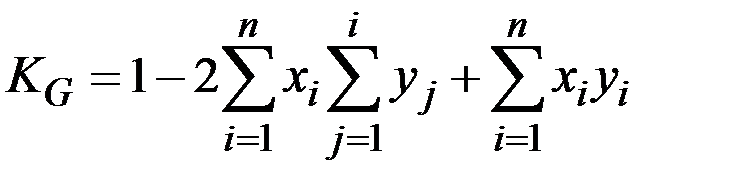 ,
,
где xi – доля населения, принадлежащая к i–й социальной группе в общей численности населения;
yi – доля доходов, сосредоточенная у i–й группы населения;
n – число социальных групп.
При равномерном распределении доходов коэффициент Джини стремится к нулю. Чем выше поляризация доходов в обществе, тем ближе этот коэффициент к единице.
Для графического изображения степени неравномерности в распределении доходов строится кривая Лоренца. При равномерном распределении доходов каждая 20%–я группа населения имела бы пятую часть доходов общества. На рис. 3.3 это изображается диагональю квадрата, что означает равномерное распределение.
При неравномерном распределении «линия концентрации» представляет собой вогнутую вниз кривую. Чем больше отклонение кривой Лоренца от диагонали квадрата, тем выше поляризация доходов общества.
Коэффициент Джини можно рассчитать по кривой Лоренца как отношение площади фигуры, образуемой кривой Лоренца и линией равномерного распределения (Sa), к площади треугольника ниже линии равномерного распределения (Sa + b): 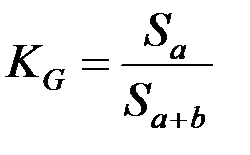 .
.
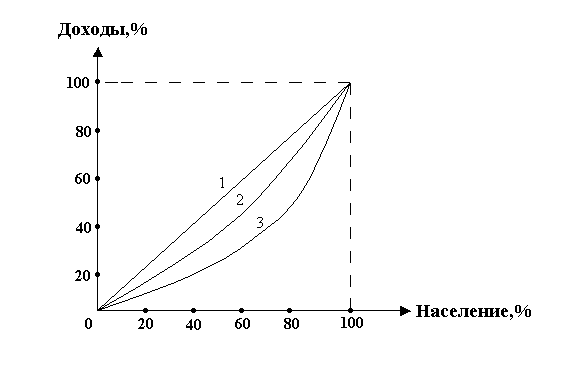
Рис. 3.3. Кривая Лоренца:
1 – линия равномерного распределения,
2, 3 – линии фактического распределения для двух периодов
Результаты расчётов представлены в табл. 3.8.
Таблица 3.8
Результаты расчётов задачи
|
Год
| Социальная группа населения | Доля населения, xi | Доля в общем объёме доходов, yi | Расчётные показатели | ||
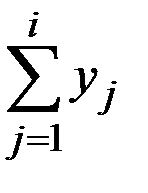
| xiyi | 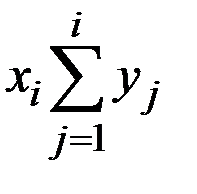
| ||||
| Базис–ный
| 1 2 3 4 5 | 0,2 0,2 0,2 0,2 0,2 | 0,098 0,149 0,188 0,238 0,327 | 0,098 0,247 0,435 0,673 1,0 | 0,0196 0,0298 0,0376 0,0476 0,0654 | 0,0196 0,0494 0,0870 0,1346 0,2000 |
| ИТОГО | 1,0 | 1,0 | – | 0,2 | 0,4906 | |
| Отчёт–ный
| 1 2 3 4 5 | 0,2 0,2 0,2 0,2 0,2 | 0,065 0,106 0,165 0,225 0,439 | 0,065 0,171 0,336 0,561 1,0 | 0,0130 0,0212 0,0330 0,0450 0,0878 | 0,0130 0,0342 0,0672 0,1122 0,2000 |
| ИТОГО | 1,0 | 1,0 | – | 0,2 | 0,4266 | |
Коэффициент Джини равен:
для базисного года:
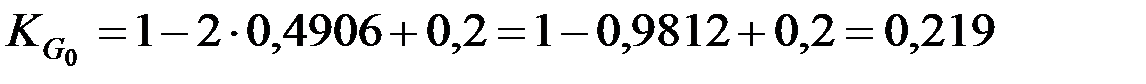 ;
;
для отчётного года:
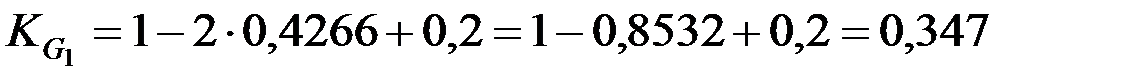 .
.
Кривая Лоренца (рис. 3.2) иллюстрирует усиление неравномерности в распределении общего объёма денежных доходов в отчётном году по сравнению с базисным.
Так, наиболее обеспеченная группа населения сконцентрировала в отчётном году 43,9% доходов против 32,7% в базисном, а доля наименее обеспеченной группы в общем доходе снизилась с 9,8 до 6,5%.
Индекс коэффициента концентрации доходов Джини:
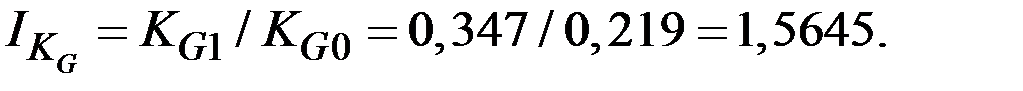
Пример 3.19. Имеются следующие данные по фирме о производстве продукции и численности работников:
|
Филиалы | Базисный период | Отчётный период | ||
| Выпуск продукции, млн. руб. | Среднесписочная численность работников, чел | Выпуск продукции, млн. руб. | Среднесписочная численность работников, чел | |
| № 1 | 150 | 100 | 140 | 130 |
| № 2 | 110 | 90 | 135 | 80 |
Определить:
1. Уровни и динамику производительности труда по каждому филиалу фирмы.
2. По двум филиалам вместе: индексы производительности труда переменного, постоянного состава и структурных сдвигов.
3. Абсолютное изменение производительности труда фирмы в целом и за счёт отдельных факторов.
4. Абсолютное изменение выпуска продукции вследствие изменения среднесписочной численности работников, производительности труда и двух факторов вместе. Сделайте выводы.
Решение. Производительности труда – это отношение объёма выпуска к среднесписочной численности работников продукции (млн. руб./ чел.).
1. Имеем значения производительности по периодам и филиалам:
| Филиал | Базисный период | Отчётный период |
| № 1 | 1,5 | 1,077 |
| № 2 | 1,222 | 1,6875 |
Динамику производительности труда по каждому филиалу охарактеризуем индивидуальным индексом:
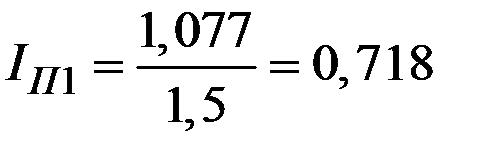 ;
;
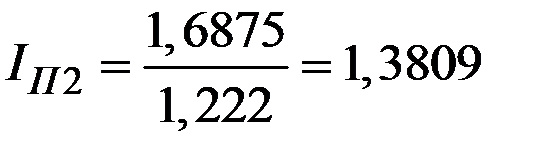 .
.
2. Средняя производительность фирмы в отчётный период:
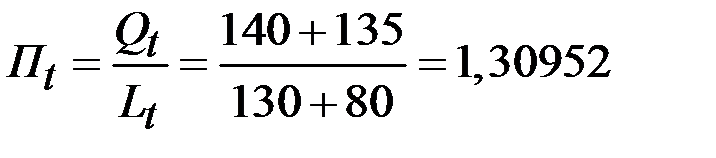 .
.
Средняя производительность фирмы в базовый период:
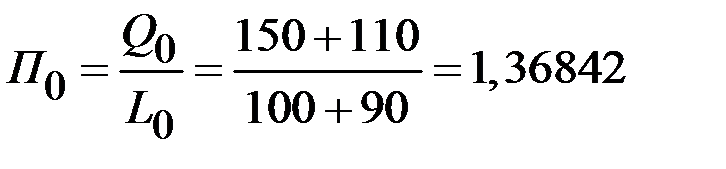 .
.
2.1. Индекс производительности труда переменного состава:
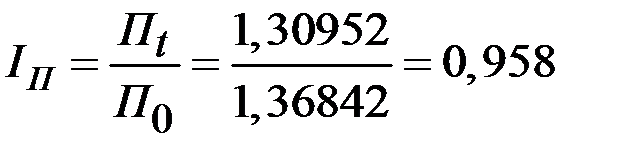 .
.
Средняя производительность фирмы уменьшилась на 4,2% по сравнению с базовым периодом.
2.2. Производительность труда постоянного состава:
– в отчётном периоде: 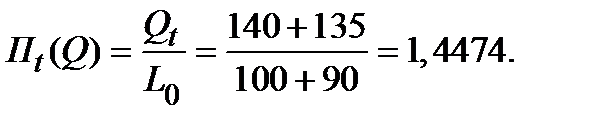
– в базовом периоде: 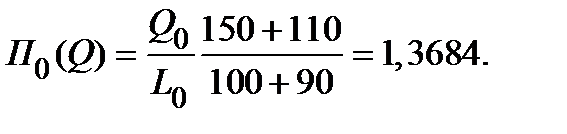
Индекс производительности труда постоянного состава:
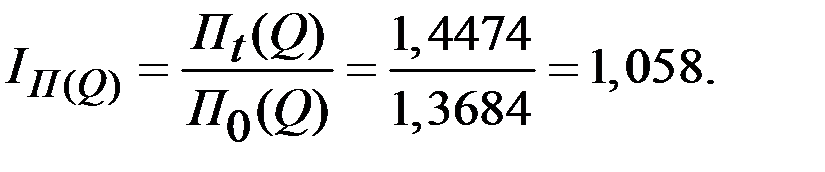
Средняя производительность фирмы, за счёт увеличения выпуска продукции, увеличилась на 5,8% по сравнению с базовым периодом.
2.3. Производительность труда в отчётном периоде:
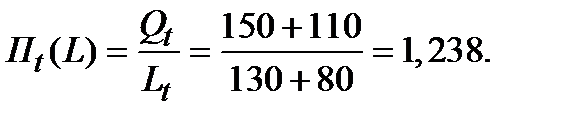
Производительность труда в базовом периоде (при новой численности и базовом объёме выпуска):
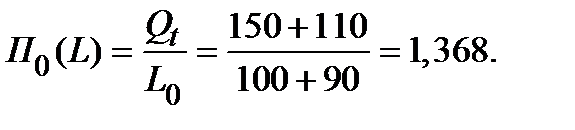
Индекс структурных сдвигов (за счёт численности):
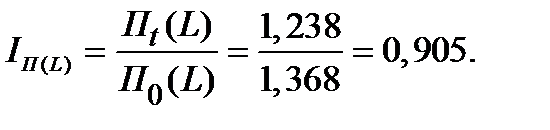
Средняя производительность фирмы, за счёт увеличения среднесписочной численности работников, уменьшилась на 9,5% по сравнению с базовым периодом.
Проверка:
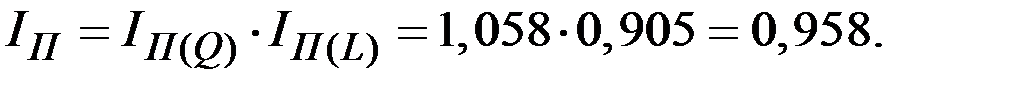
3.1. Абсолютное изменение производительности труда в целом по фирме составит величину
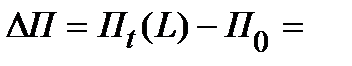 1,30952 – 1,36842 = – 0,0589 млн. руб./чел.
1,30952 – 1,36842 = – 0,0589 млн. руб./чел.
3.2. Абсолютное изменение производительности труда по фирме за счёт изменения численности работников составит величину
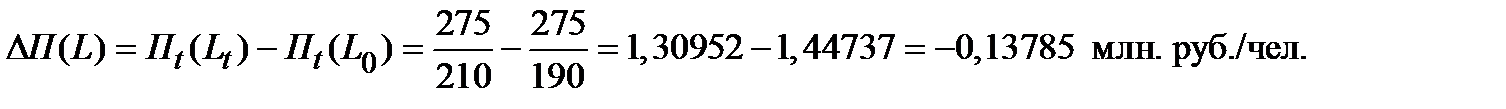
3.3. Абсолютное изменение производительности труда по фирме за счёт изменения объёмов выпуска продукции составит величину
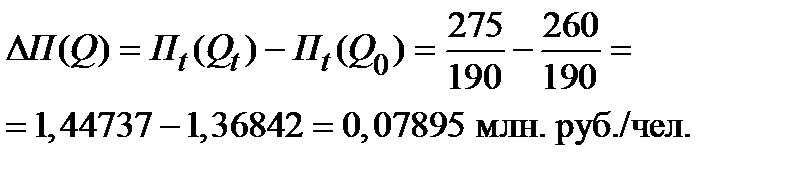
Проверка:
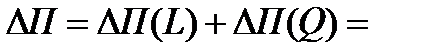 – 0,0589 = – 0,13785 + 0,07895.
– 0,0589 = – 0,13785 + 0,07895.
4.1. Абсолютное изменение объёма выпуска продукции вследствие изменения среднесписочной численности работников составит величину
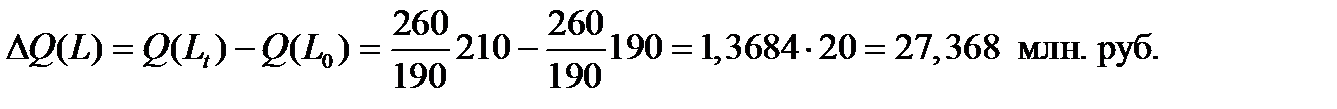
4.2. Абсолютное изменение выпуска продукции вследствие изменения производительности труда составит величину
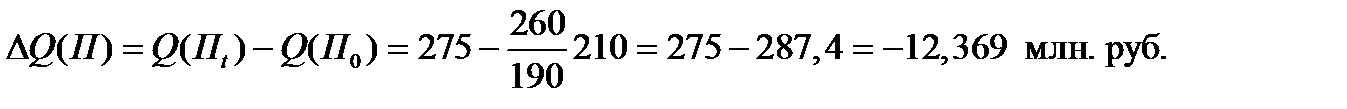
4.3. Абсолютное изменение выпуска продукции вследствие изменения двух факторов вместе составит величину:
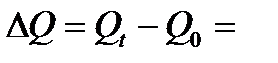 275 – 260 = 15 млн. руб.
275 – 260 = 15 млн. руб.
Проверка:
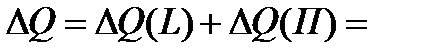 – 12,369 + 27,368 = 15 млн. руб.
– 12,369 + 27,368 = 15 млн. руб.
Пример 3.20. Известны объёмы выпуска продукции и их себестоимость в текущем и базисном периодах:
| Вид продукции | Объём выпуска | Себестоимость, тыс. руб./ед. | ||
| Базисный | Отчётный | Базисный | Отчётный | |
| А, м. | 300 | 250 | 8 | 10 |
| В, тн. | 400 | 470 | 60 | 80 |
| С, шт. | 50 | 66 | 20 | 35 |
Определить: индексы себестоимости постоянного состава, переменного состава, структурных сдвигов, т.е., на сколько процентов изменение среднего уровня себестоимости производства продукции обусловлено изменением самой себестоимости как таковой и на сколько процентов изменением структуры производства.
Решение. 1. Индекс себестоимости переменного состава
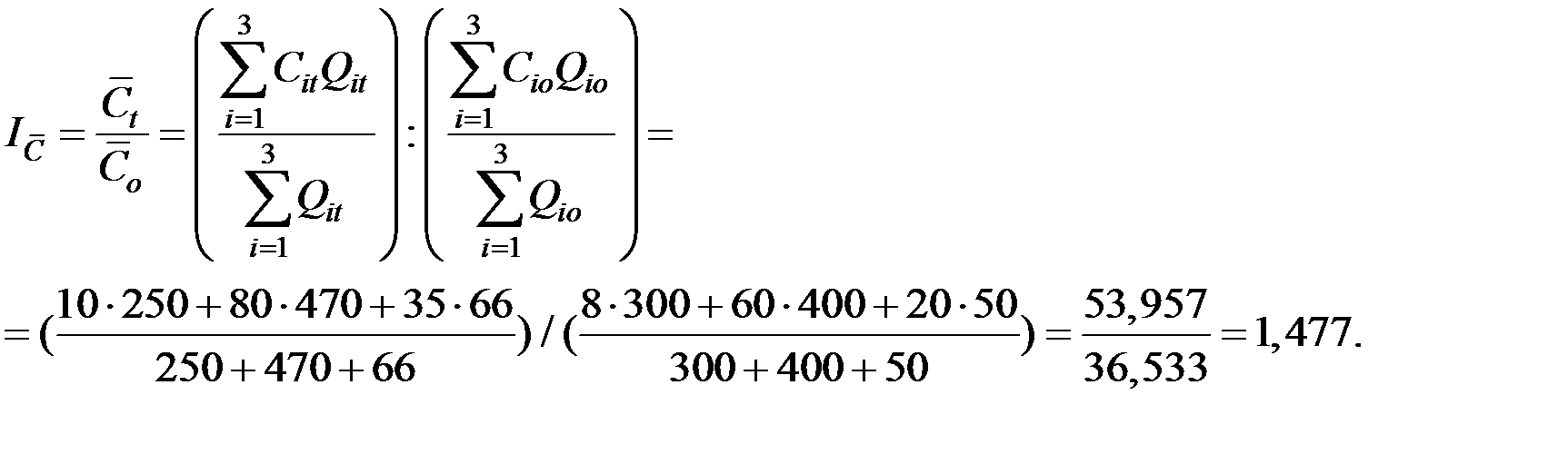
2. Индекс себестоимости постоянного состава
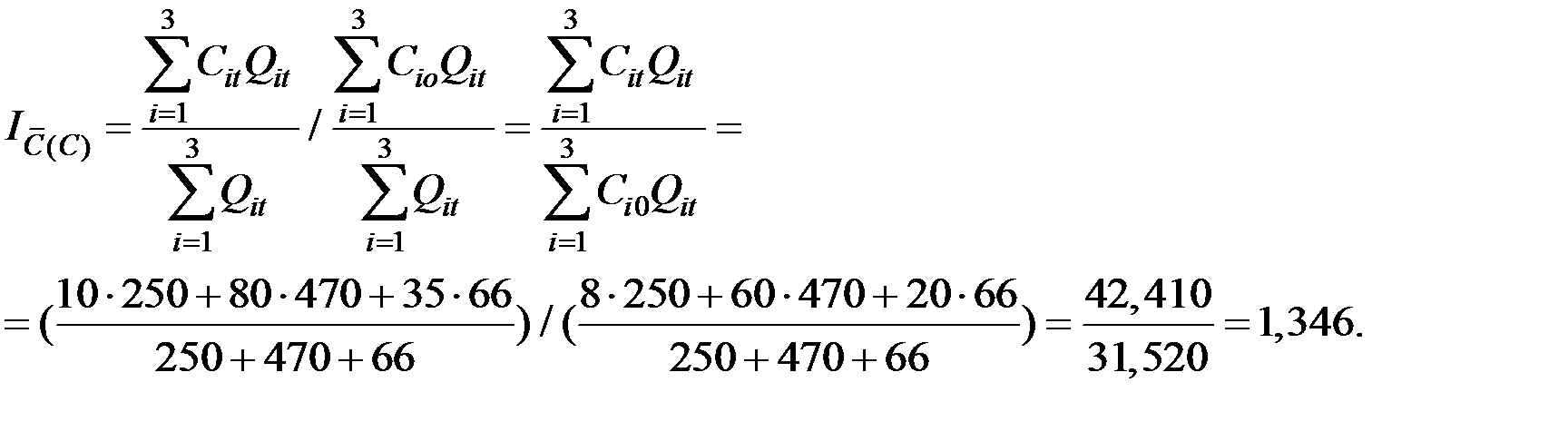
3. Индекс себестоимости структурных сдвигов
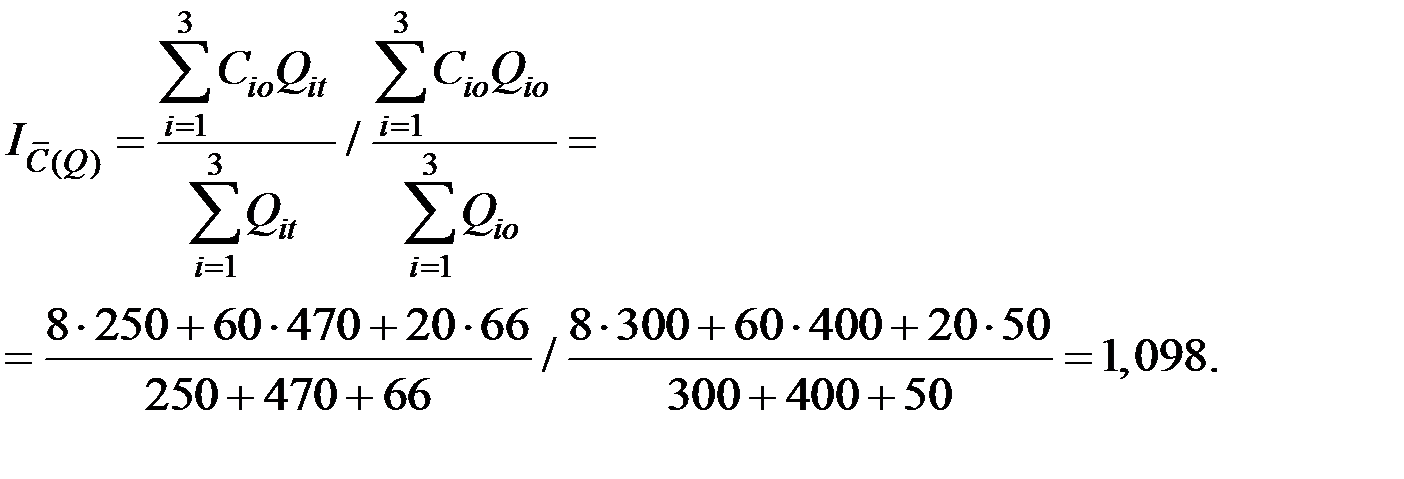
Проверка: 
Пример 3.21. Известны объёмы производства и затраты времени на единицу продукции в базовом и отчётном периодах
| Вид продукции | Производство продукции, ед. | Затраты времени на производство ед., чел. часов | ||
| Базисный | Отчётный | Базисный | Отчётный | |
| А, м. | 2000 | 300 | 100 | 80 |
| В, шт. | 900 | 700 | 60 | 50 |
Определить:
1. Индивидуальные и сводные индексы производительности труда и трудоёмкости.
2. Индивидуальные и сводный индексы физического объёма.
3. Сводный индекс затрат труда на производство продукции.
4. Экономию затрат труда на производство продукции за счёт роста производительности труда.
5. Экономию затрат труда в общем случае.
Решение.
1. Индивидуальные индексы производительности труда
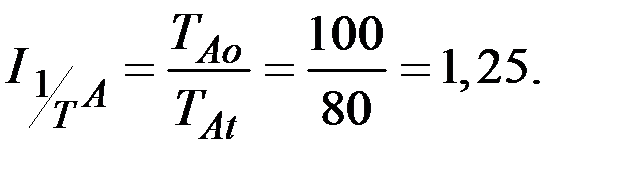
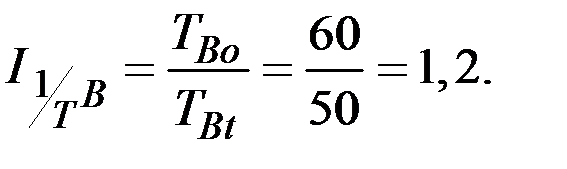
Индивидуальные индексы трудоёмкости
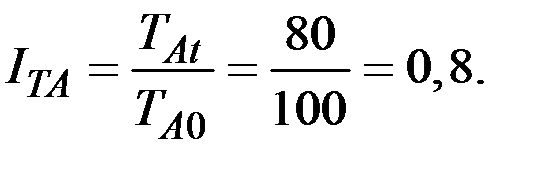
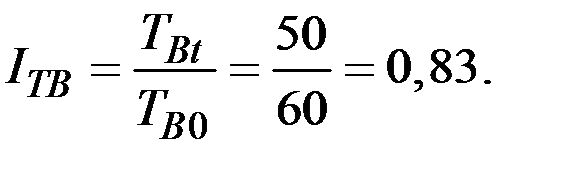
Сводный индекс производительности труда

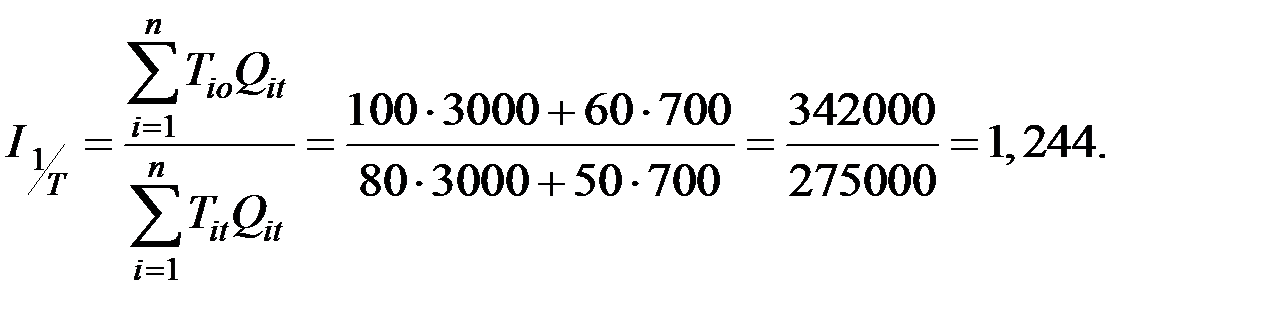
Сводный индекс трудоёмкости:

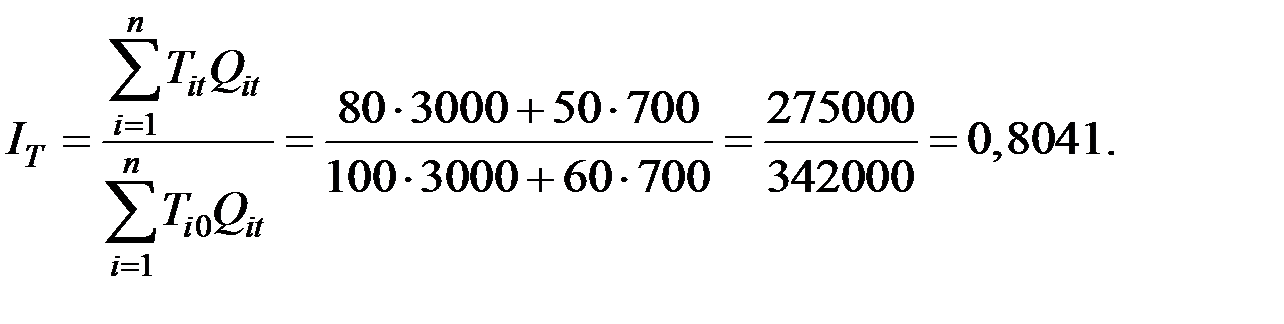
2. Индивидуальные индексы физического объёма продукции
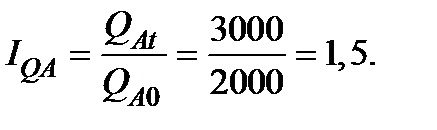
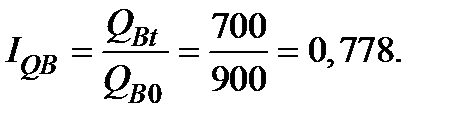
Сводный индекс физического объёма продукции
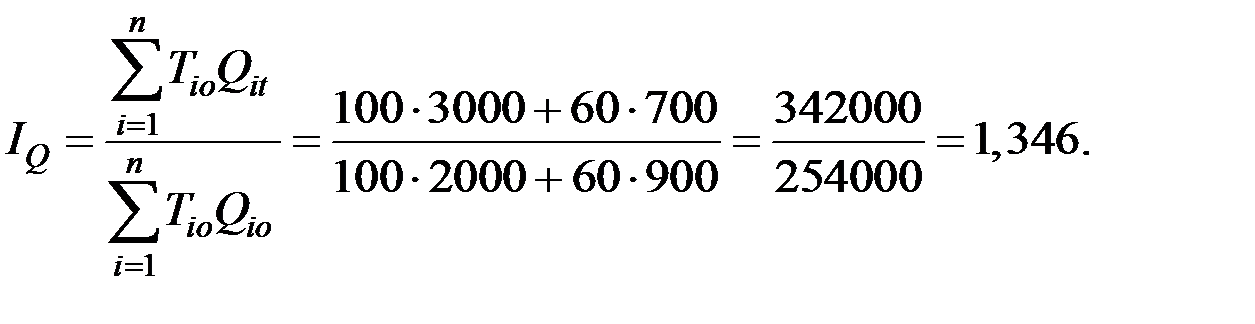
3. Сводный индекс затрат труда на производство продукции
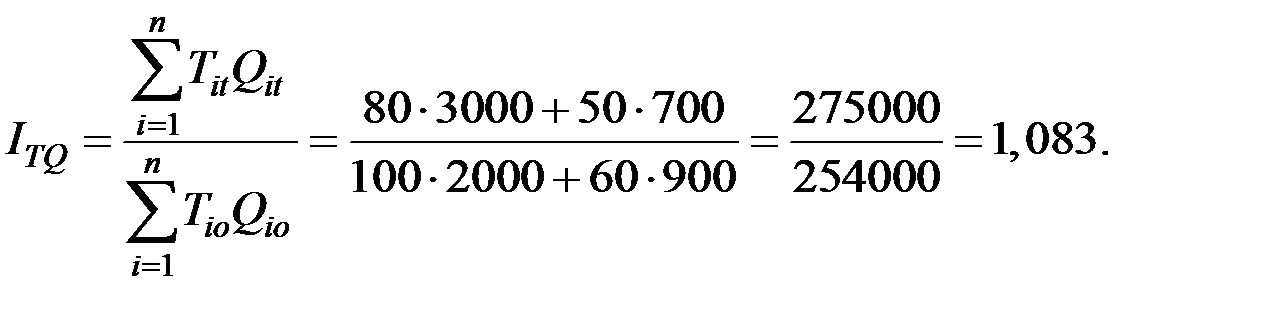
4. Увеличение затрат труда (человеко–часов) на производство продукции за счёт роста производительности труда составит
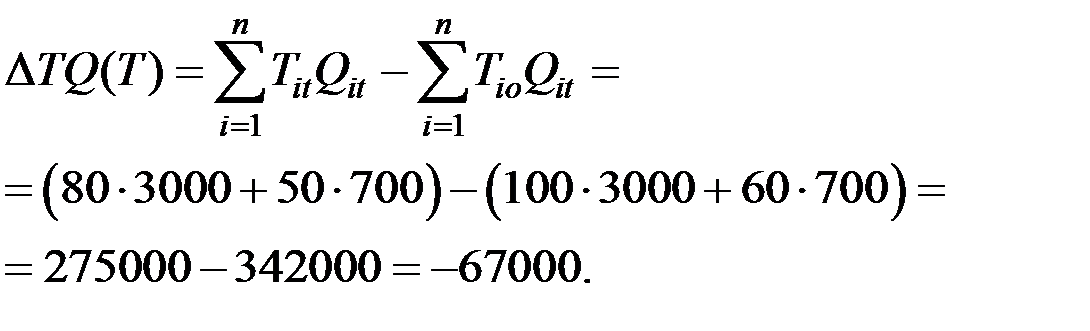
Это экономия.
5. Увеличение затрат труда в общем случае составит величину
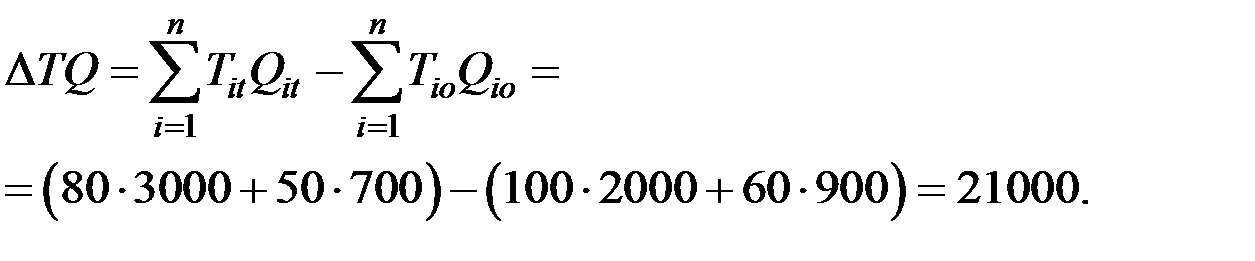
Контрольные вопросы к главе 3
1. Что такое моментный и интервальный ряды динамики?
2. Охарактеризуйте понятия: темп роста, темп прироста, средний уровень ряда, коэффициент опережения, смыкание рядов динамики.
3. Какова взаимосвязь темпов роста и темпов прироста ряда?
4. Что означает абсолютное значение одного процента прироста?
5. Какова взаимосвязь относительных и абсолютных приростов ряда?
6. Как вычисляется среднегодовой темп роста?
7. Как вычисляется индексы сезонности ряда?
8. Как аналитически описать динамику ряда?
9. Охарактеризуйте понятие эластичности и её свойства.
10. Как определяются средние обобщающие характеристики ряда?
11. Что такое смыкание рядов динамики?
12. Какова роль индексного метода анализа в экономике?
13. В чём различие агрегатных индексов Ласпейреса, Пааше, Фишера?
14. Какие виды средних индексов используются в статистике?
15. Что характеризует индекс влияния структурных сдвигов?
ЗАДАНИЕ 3.1. Имеются статистические данные (табл. 3.9) о динамике некоторых показателей фирмы за 2008 – 2014 гг. (в сопоставимых единицах измерения).
Определить аналитические и средние обобщающие характеристики ряда динамики показателей за 2008 – 2014 гг.:
1) абсолютные приросты;
2) темпы роста;
3) темпы прироста;
4) абсолютные значения одного процента прироста;
5) средние обобщающие характеристики ряда динамики (средний уровень ряда, среднегодовой темп роста и прироста показателя за исследуемый период);
6) выявить основную тенденцию развития показателя за 2008 – 2014 гг. методом скользящей средней и методом аналитического выравнивания.
ЗАДАНИЕ 3.2. Определить месячные индексы сезонности по имеющимся статистическим данным за 36 месяцев (2012 – 2014 гг.) (табл. 3.10).
Графически представить результаты расчётов.
Таблица 3.9
Исходные данные для расчёта (по вариантам)
| № | Показатель | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 |
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 | Отчисления в бюджет, тыс.р. Основные фонды, млн. руб. Средняя зарплата одного работника, руб./мес. Месячная прибыль, тыс. руб. Потребляемое количество электроэнергии, тыс. квт. Расход топлива, тыс. литров Количество специалистов с высшим образованием Доходы от портфеля ценных бумаг, тыс. руб. Среднемесячные премии, руб. Затраты на охрану труда, тыс.р. Затраты на экологию, тыс. руб. Валовые издержки фирмы, тыс. руб./мес. Капитал акций, тыс. руб. Собственный капитал фирмы, млн. руб. Отчисления в пенсионный фонд, тыс. руб. Затраты на страхование, тыс. р. Себестоимость продукции, руб. Отчисления в благотворительный фонд, тыс. руб. Затраты на амортизацию оборудования, тыс. руб. Кредиты, тыс. руб. Налоги, тыс. руб. Средняя выработка одного рабочего, тыс. руб. Затраты на строительство жилья, тыс. руб. Количество специалистов с экономическим образованием Затраты на рекламу, тыс. руб. Отчисления в фонд эконом. стимулирования, тыс. руб. Акцизы, тыс. руб. | 79 40 850 300 10 90 8 313 500 200 135 30 900 45 250 160 1500 210 145 500 200 54 356 5 15 85 450 | 85 44 900 325 12 150 9 316 450 230 146 40 963 60 256 163 1510 240 150 510 213 56 361 7 16 108 556 | 90 46 970 340 13 160 12 320 510 256 149 52 996 66 260 167 1569 266 161 511 219 58 372 8 18 121 666 | 100 54 1080 345 18 140 12 345 530 261 152 56 1069 68 262 173 1623 271 187 523 223 60 400 8 19 106 700 | 110 60 1700 360 25 200 15 345 536 246 159 58 1100 95 264 180 1689 283 190 529 225 63 412 9 24 128 800 | 150 90 1900 354 27 240 16 354 523 256 163 59 1200 99 269 191 1700 290 199 530 229 78 421 10 21 133 840 | 170 120 2800 370 35 260 20 357 540 269 174 64 1333 130 274 200 1720 310 210 549 235 81 450 14 29 140 850 |
Таблица 3.10
Исходные данные для расчёта (по вариантам)
| № | Показатель | Год | Значения по месяцам (январь–декабрь) |
| 1. | Реализация сахара фирмой (тонн) | 2012 2013 2014 | 50, 51, 57, 100, 120, 140, 200, 220, 110, 90, 80, 70 51, 53, 54, 95, 130, 145, 205, 210, 115, 95, 85, 75 54, 55, 60, 105, 140, 150, 210, 220, 120, 100, 90, 80 |
| 2. | Прибыль фирмы (тыс.р./мес.) | 2012 2013 2014 | 8,4; 9,7; 10,3; 10,7; 9,9; 12; 13; 15,1; 9,9; 9,8; 10,2; 8,9 8,8; 10; 11,3; 10,9; 10,3; 12; 14; 14; 10,9; 10,8; 10; 10 9,3; 11,2; 11,4; 10,2; 11,7; 12; 15; 16; 11,1; 11,2; 11; 9 |
| 3. | Рентабельность средств предприятия (%) | 2012 2013 2014 | 22 24,5 21,8 19,7 22,3 24,1 22,8 21,8 21,5 20,4 20,7 21,5 21,2 20, 20,8 21,4 21,6 21,9 22,0 22,8 19,7 21,4 22,9 22,1 22,3 21 21,3 21,7 22,3 24,5 21,8 24,1 22,8 20,4 20,7 21,4 |
| 4. | Процентная ставка кредита (%) | 2012 2013 2014 | 32, 20, 28, 27, 29, 30, 37, 32, 25, 28, 25, 22 30, 20, 25, 24, 26, 25, 28, 28, 24, 26, 20, 22 29, 22, 27, 27, 30, 29, 27, 27, 24, 23, 20, 21 |
| 5. | Валовые издержки предприятия (тыс. р./мес.) | 2012 2013 2014 | 30, 40, 52, 44, 37, 38, 42, 41, 44, 33, 38, 41 39, 37, 42, 53, 50, 49, 51, 46, 45, 40, 42, 51 52, 47, 46, 54, 38, 61, 57, 50, 44, 47, 45, 50 |
| 6. | Оборотные фонды предприятия (млн. руб.) | 2012 2013 2014 | 90, 70, 82, 91, 114, 103, 120 85, 74, 63, 84, 96 87, 80, 85, 74, 113, 105, 123, 87, 78, 81, 82, 93 96, 91, 99, 81, 117, 107, 125, 98, 70, 76, 84, 96 |
| 7. | Уровень инфляции (% в месяц) | 2012 2013 2014 | 3,1 3,7 6,4 3,8 4,2 3,0 3,2 3,7 3,0 3,1 3,6 4,1 4,8 5,5 3,0 3,1 3,2 3,0 3,7 3,5 3,1 3,2 3,0 3,1 3,0 3,4 3,5 3,6 4,1 3,7 4,2 3,8 4,6 4,7 5,1 5,8 |
| 8. | Экономическая рентабельность предприятия (%) | 2012 2013 2014 | 19,7 20,4 22,8 20,7 21,2 20,3 20,4 20,3 20,7 22,1 22,7 19 21,2 21,7 21,2 21,4 21,6 20,4 20,5 21,7 21 20,6 20,8 20,9 22 19,7 20,1 23,0 20,4 22,3 22,7 21,4 21,5 19,7 20,4 20,9 |
| 9. | Валовая продукция цеха (тыс. руб./мес.) | 2012 2013 2014 | 160 172 168 173 194 189 171 172 160 171 168 164 158 172 171 170 196 184 167 178 159 173 170 164 160 173 165 166 196 186 170 174 158 171 172 168 |
| 10. | Потребление мяса по району (тонн) | 2012 2013 2014 | 38, 36, 37, 36, 32, 30, 24, 16, 18, 32, 42, 59 35, 36, 35, 36, 32, 31, 23, 17, 18, 30, 44, 53 37, 39, 37, 40, 38, 31, 24, 15, 19, 31, 46, 52 |
| 11. | Товарооборот на одного работника (тыс. руб.) | 2012 2013 2014 | 99, 116, 137, 136, 132, 130, 124, 116, 118, 132, 142, 139 85, 106, 135, 136, 132, 131, 123, 117, 118, 130, 144, 133 87, 119, 137, 140, 138, 121, 124, 115, 119, 131, 146, 132 |
| 12. | Ввод жилья по городу (тыс. м 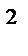 ) )
| 2012 2013 2014 | 10,8 10,4 17,3 20,1 15,3 23,7 34,2 32,1 21,3 22 18,4 13,4 18,3 14,7 16,0 17,9 16,2 26,4 35,8 39,3 28,6 23 18,1 19,4 12,8 15,4 18,3 20,1 16,3 23,7 34,2 32,4 21,3 21 18,6 14,4 |
| 13. | Коэффициент изношенности основных фондов | 2012 2013 2014 | 0,6 0,71 0,64 0,79 0,5 0,59 0,64 0,7 0,8 0,67 0,69 0,71 0,8 0,74 0,7 0,72 0,6 0,84 0,76 0,78 0,69 0,66 0,6 0,8 0,62 0,71 0,6 0,79 0,5 0,59 0,64 0,7 0,82 0,67 0,69 0,73 |
| 14. | Количество выполненных заказов | 2012 2013 2014 | 83, 40, 64, 69, 72, 80, 24, 18, 44, 70, 53, 58 20, 36 46, 54, 64, 33, 47, 35, 47, 35, 84, 77 56, 54, 95, 51, 48, 40, 35, 44, 47, 64, 53, 33 |
| 15. | Выручка от реализации продукции (тыс. руб.) | 2012 2013 2014 | 570 592 604 680 730 654 642 686 672 591 703 606 574 688 608 630 650 644 666 682 599 704 710 612 520 656 642 610 670 594 600 700 681 676 647 610 |
| 16. | Объём продаж (тыс. руб.) | 2012 2013 2014 | 99, 116, 137, 136, 139, 200, 194, 146, 138, 132, 142, 130 95, 106, 135, 136, 132, 221, 193, 147, 148, 130, 144, 133 97, 119, 137, 140, 138, 211, 194, 155, 149, 131, 146, 152 |
| 17. | Процент премии на предприятии | 2012 2013 2014 | 25, 16, 19, 19, 20, 35, 17, 18, 12, 18, 21, 65 25, 16, 18, 21, 19, 45, 15, 16, 18, 16, 20, 69 28, 16, 21, 23, 17, 49, 19, 20, 18, 16, 20, 68 |
| 18. | Количество обслуженных клиентов) | 2012 2013 2014 | 171 183 169 175 173 177 189 191 168 171 177 179 180 182 190 179 147 172 172 173 170 171 172 175 165 181 173 174 174 175 166 168 171 173 186 178 |
| 19. | Средняя зарплата на предприятии (усл. ед.) | 2012 2013 2014 | 3,4 2,8 7,1 6,2 4,4 4,7 4,9 5,0 5,1 3,8 3,9 4,7 4,5 5,7 5,8 6,3 6,4 5,9 7,7 6,2 4,4 5,6 5,0 6,0 6,0 6,9 6,1 6,5 5,9 5,8 5,7 5,9 6,1 6,2 6,4 6,4 |
| 20. | Потребление хлебопродуктов по городу (тонн) | 2012 2013 2014 | 18,7 20 22,8 20,7 21,3 20,3 20,4 20,3 20,9 22,1 22,7 18,1 21,9 21,7 21,2 21 21,6 20,4 20,5 21,7 21,9 20,6 20,8 22,9 22 19,7 20,1 23,0 20,4 22,3 21,7 21,4 21,8 19,7 20,4 19,9 |
| 21. | Количество сделок (договоров) фирмы | 2012 2013 2014 | 156 152 168 221 202 258 217 182 221 232 184 144 154 163 179 211 192 254 224 233 222 214 192 142 173 162 213 233 197 295 215 209 287 269 184 153 |
| 22. | Количество проданных холодильников | 2012 2013 2014 | 151 152 168 221 202 258 217 222 221 232 184 157 154 163 179 211 192 254 224 233 222 214 192 182 163 162 183 233 197 295 215 229 287 269 204 183 |
| 23. | Месячный процент премии на предприятии (%) | 2012 2013 2014 | 39, 16, 17, 17, 26, 15, 17, 18, 22, 18, 16, 23, 30, 16, 18, 21, 31, 25, 15, 16, 18, 16, 20, 21, 18, 32, 21, 23, 17, 32, 19, 20, 15, 16, 20, 32 |
| 24. | Себестоимость добычи одной тонны руды (руб.) | 2012 2013 2014 | 10,8 10,4 17,3 10,1 15,3 23,7 10,2 12,1 11,3 12 10,4 13,4 10,3 10,7 11,0 12,9 13,2 12,4 15,8 19,3 10,6 8,8 10,1 9,4 9,7 11,4 10,2 10,4 10,3 10,9 13,7 9,1 9,4 10,8 10,2 10,1 |
| 25. | Расход воды (т.) | 2012 2013 2014 | 171 162 198 221 202 258 217 182 221 232 184 151 174 163 199 211 192 254 224 193 222 214 202 182 183 162 213 233 197 295 215 209 287 269 204 183 |
| 26. | Количество проданных пылесосов | 2012 2013 2014 | 149 152 168 221 202 258 217 222 221 232 184 157 152 163 179 211 192 254 224 233 222 214 192 182 160 162 183 233 197 295 215 229 287 269 204 183 |
| 27. | Объём выпуска продукции (тыс. руб.) | 2012 2013 2014 | 100, 99, 137, 136, 139, 200, 194, 146, 138, 132, 142, 130 98, 106, 135, 136, 132, 221, 193, 147, 148, 130, 144, 133 101, 99, 137, 140, 138, 211, 194, 155, 149, 131, 146, 152 |
ЗАДАНИЕ 3.3. В табл. 3.11 для трёх условных предприятий приведены данные о выработке однородной продукции (тонн) и о затратах времени (человеко–часов) на выработку 1 тонны продукции за базовый и отчётный периоды. По данным табл. 3.11 определить сводные индексы производительности труда постоянного состава, переменного состава и структурных сдвигов.
Таблица 3.11
Исходные данные по вариантам
| № п/п | Предприятие 1 | Предприятие 2 | Предприятие 3 | |||||||||
| Выработка продукции, т. | Затраты чел.–час на 1 т. | Выработка продукции, т. | Затраты чел.–час на 1 т. | Выработка продукции, т. | Затраты чел.–час на 1 т. | |||||||
| Баз. | Отч. | Баз. | Отч. | Баз. | Отч. | Баз. | Отч. | Баз. | Отч. | Баз. | Отч. | |
| 1 | 14 | 16 | 30 | 25 | 23 | 31 | 25 | 26 | 32 | 48 | 20 | 17 |
| 2 | 30 | 25 | 23 | 31 | 40 | 35 | 43 | 41 | 60 | 65 | 83 | 81 |
| 3 | 16 | 18 | 30 | 25 | 20 | 30 | 20 | 27 | 11 | 12 | 13 | 14 |
| 4 | 26 | 32 | 25 | 22 | 80 | 85 | 40 | 68 | 25 | 28 | 23 | 26 |
| 5 | 31 | 48 | 21 | 15 | 33 | 43 | 27 | 38 | 20 | 30 | 23 | 27 |
| 6 | 21 | 30 | 20 | 27 | 16 | 18 | 30 | 25 | 80 | 85 | 40 | 68 |
| 7 | 80 | 85 | 40 | 68 | 26 | 32 | 25 | 22 | 30 | 46 | 20 | 15 |
| 8 | 200 | 300 | 100 | 95 | 310 | 480 | 120 | 115 | 340 | 480 | 110 | 125 |
| 9 | 90 | 70 | 60 | 65 | 45 | 55 | 40 | 50 | 75 | 85 | 52 | 57 |
| 10 | 32 | 25 | 22 | 80 | 31 | 40 | 35 | 43 | 16 | 18 | 30 | 25 |
| 11 | 48 | 22 | 15 | 33 | 25 | 20 | 30 | 20 | 26 | 32 | 25 | 22 |
| 12 | 30 | 20 | 27 | 16 | 22 | 80 | 85 | 40 | 31 | 48 | 20 | 15 |
| 13 | 100 | 120 | 150 | 99 | 100 | 120 | 154 | 119 | 88 | 111 | 120 | 118 |
| 14 | 55 | 40 | 60 | 50 | 55 | 40 | 54 | 53 | 55 | 40 | 60 | 64 |
| 15 | 27 | 30 | 26 | 22 | 20 | 30 | 16 | 21 | 20 | 37 | 18 | 26 |
| 16 | 20 | 30 | 20 | 27 | 14 | 16 | 30 | 25 | 32 | 48 | 20 | 17 |
| 17 | 82 | 85 | 47 | 68 | 30 | 25 | 23 | 31 | 60 | 65 | 83 | 81 |
| 18 | 80 | 85 | 40 | 68 | 25 | 28 | 23 | 26 | 90 | 95 | 104 | 115 |
| 19 | 33 | 43 | 27 | 38 | 20 | 30 | 20 | 27 | 60 | 65 | 83 | 81 |
| 20 | 16 | 18 | 30 | 25 | 80 | 85 | 41 | 68 | 90 | 95 | 104 | 115 |
| 21 | 60 | 65 | 83 | 81 | 84 | 85 | 40 | 68 | 25 | 28 | 23 | 26 |
| 22 | 90 | 95 | 104 | 115 | 93 | 93 | 127 | 138 | 120 | 130 | 112 | 127 |
| 23 | 100 | 120 | 154 | 190 | 88 | 111 | 120 | 140 | 120 | 130 | 112 | 127 |
| 24 | 55 | 40 | 30 | 37 | 55 | 40 | 26 | 80 | 85 | 40 | 68 | 80 |
| 25 | 20 | 30 | 21 | 25 | 20 | 37 | 28 | 33 | 43 | 27 | 38 | 33 |
| 26 | 27 | 37 | 20 | 27 | 40 | 44 | 54 | 43 | 88 | 111 | 120 | 118 |
| 27 | 83 | 85 | 60 | 68 | 55 | 46 | 70 | 83 | 55 | 42 | 60 | 40 |
| 28 | 33 | 43 | 27 | 38 | 20 | 30 | 60 | 70 | 20 | 37 | 30 | 56 |
Дата: 2019-03-05, просмотров: 634.