Основные понятия и характеристики динамики показателей
Рядом динамики называется ряд чисел, характеризующих изменение явления (показателя) во времени. Каждый ряд динамики состоит из двух элементов: 1) периодов (моментов) времени; 2) уровней (значений).
Значения показателей, образующих ряд динамики, называют уровнем ряда и обычно обозначают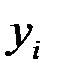 
.
Ряды динамики подразделяют на ряды динамики абсолютных, средних и относительных величин.
По признаку времени ряды динамики абсолютных величин подразделяют на моментные и интервальные ряды динамики.
Моментный ряд динамики – это ряд, который образуют показатели, характеризующие состояние явления на тот или иной момент времени.
Интервальный ряд динамики – ряд, который образуют показатели, характеризующие явление за тот или иной период времени.
Для общей характеристики уровня явления за тот или иной период вычисляется средняя из всех уровней ряда – средний уровень ряда.
Способ расчёта среднего уровня ряда зависит от характера ряда.
Средний уровень ряда часто определяют по формуле
,
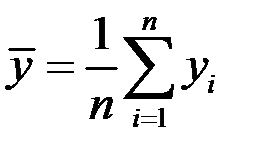где n – число членов ряда динамики.
Абсолютный прирост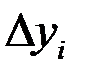 
показывает, на сколько единиц увеличился (или уменьшился) анализируемый уровень ряда 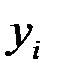относительно базисного уровня 
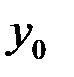(по базисной схеме) или уровня предшествующего года 
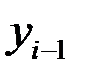(по цепной схеме).
Абсолютный прирост определяют по формулам:
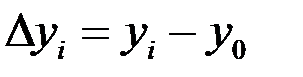(по базисной схеме),
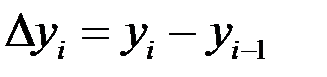(по цепной схеме).
Темп роста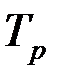 
показывает, во сколько раз анализируемый уровень ряда увеличился по сравнению с уровнем, принятым за базу сравнения (по базисной схеме) или предшествующим уровнем (по цепной схеме), или какую долю анализируемый уровень ряда составляет от уровня ряда, принятого за базу сравнения. Темп роста выражают в процентах или отвлечённых числах (коэффициент роста).
Темп роста определяют по формулам:
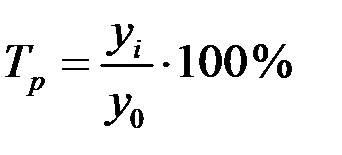(по базисной схеме),
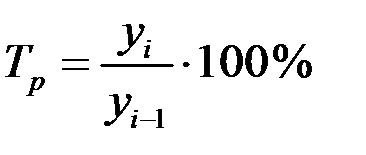(по цепной схеме).
Темп прироста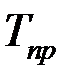 
показывает, на сколько процентов увеличился (или уменьшился) анализируемый уровень ряда по сравнению с базисным (по базисной схеме), или предшествующим уровнем ряда (по цепной схеме). Его определяют как отношение абсолютного прироста к уровню, принятому за базу сравнения по формулам:
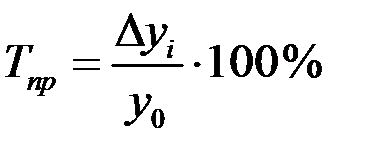(по базисной схеме).
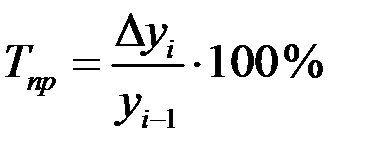(по цепной схеме).
Темпы роста и прироста связаны между собой, что видно из формул их расчёта:
.
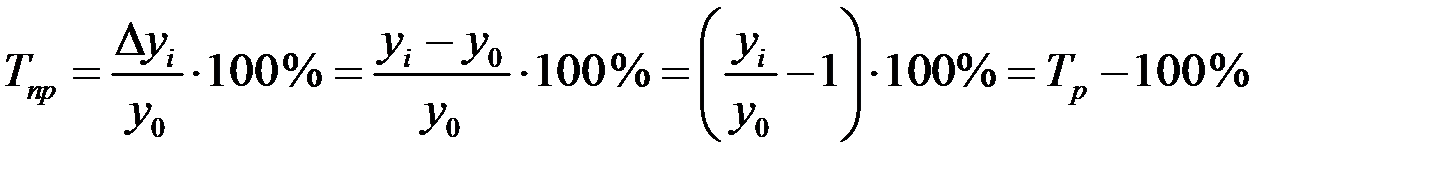Это даёт основание определить темп прироста через темп роста:
.
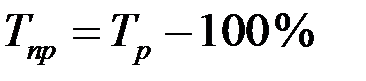Средний темп роста и средний темп прироста характеризуют соответственно темпы роста и прироста за период в целом.
Средний темп роста рассчитывается по данным ряда динамики по формуле средней геометрической:
,
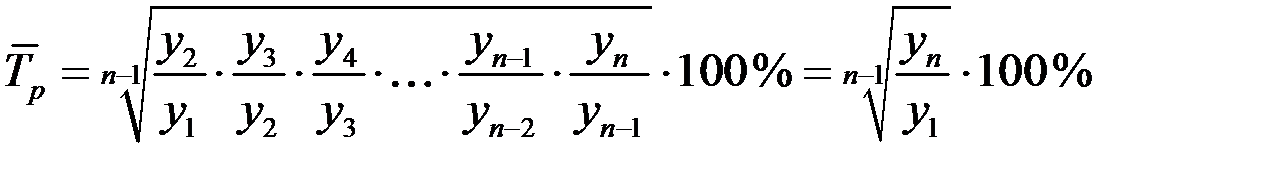где n –1 – количество цепных коэффициентов роста.
Средний темп прироста можно определить из среднего темпа роста:
.
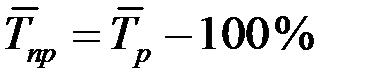Абсолютное значение одного процента прироста – это отношение абсолютного прироста к цепному темпу прироста в процентах:
.
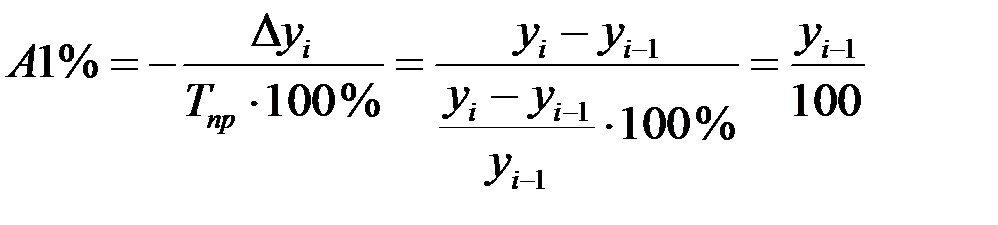Абсолютное значение одного процента прироста равно 0,01 предшествующего уровня.
Для сравнения базисных темпов роста двух изучаемых рядов динамики за анализируемый период принято исчислять коэффициент опережения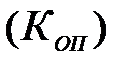 
по формуле
,
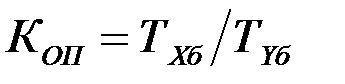где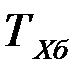 
– базисный темп роста первого ряда;
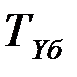– базисный темп роста второго ряда.
Уровни рядов динамики должны быть сопоставимы по методологии расчёта показателя, территории, продолжительности периодов, охватываемого объекта, единицам измерения и другим признакам.
В тех случаях, когда вначале имеются уровни ряда, исчисляемые по одной методологии или в одних границах, а затем уровни ряда, исчисляемые по другой методологии или в других границах, уровни ряда динамики оказываются несопоставимы между собой.
Чтобы привести уровни в ряду динамики к сопоставимому, годному для анализа виду, необходимо применить приём, который называют смыканием рядов динамики.
Пример 3.1. Имеются данные о поголовье скота в районе (табл. 3.1).
Привести ряды динамики к сопоставимому виду.
Таблица 3.1
Динамика поголовья скота в районе за 2008 – 2014 гг. (тыс. голов)
| № п\п | Поголовье крупного рогатого скота | Год | ||||||
| 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | ||
| 1 2 3 | В прежних границах В новых границах Сомкнутый ряд | 45,0 – 63,0 | 48,0 – 67,2 | 50,0 70,0 70,0 | – 71,3 71,3 | – 73,2 73,2 | – 74,1 74,1 | – 75,0 75,0 |
Решение. Определим коэффициент пересчёта уровней в 2010 г., в котором произошло изменение границ района:
.
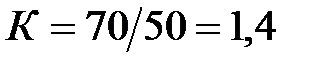Умножая на этот коэффициент уровни ряда динамики в прежних границах, приводим их к сопоставимым уровням в новых границах.
В 2008 г.: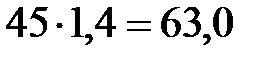 
тыс. голов;
в 2009 г.: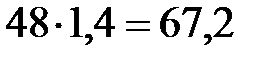 
тыс. голов.
Представим полученные данные в виде сомкнутого ряда динамики (третья строчка табл. 3.1).
Эти данные сопоставимого ряда характеризуют рост поголовья скота в районе за 2008 – 2014 гг. Они могут быть использованы для расчёта аналитических показателей ряда динамики.
Пример 3.2. Имеются данные о среднемесячной заработной плате на одного работника и стоимости набора из 25 основных продуктов питания в расчёте на одного человека в одной из областей РФ за полугодие:
| Месяц | Среднемесячная заработная плата, руб. | Стоимость набора из 25 основных продуктов питания, руб. |
| Январь Февраль Март Апрель Май Июнь | 6548 6844 7450 7465 7793 8372 | 2094 2166 2209 2241 2275 2325 |
Привести ряды динамики к одному основанию и сделать выводы.
Решение. Для сравнения показателей необходимо уровни рядов привести к одному основанию, т.е. исчислить базисные темпы роста.
Для среднемесячной заработной платы:
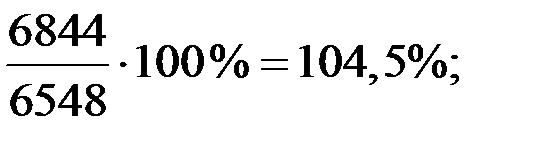
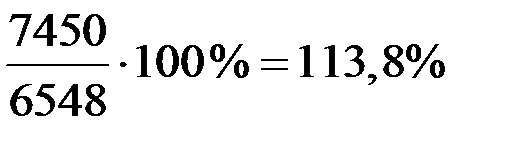и т.д.
Для стоимости набора продуктов питания:
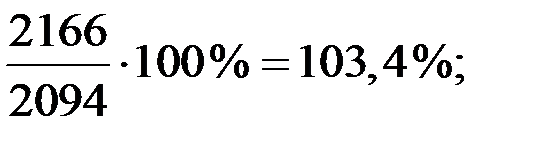
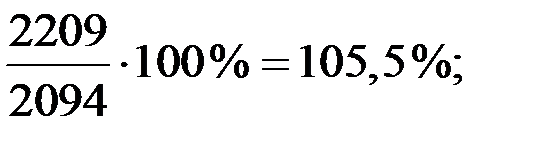и т.д.
Представим полученные результаты в табл. 3.2.
Данные табл. 3.2 показывают, что начисленная среднемесячная заработная плата на одного работника неуклонно растёт.
Прирост в июне к январю составил 27,9%.
Стоимость набора из 25 основных продуктов питания тоже растёт, но более медленными темпами.
Таблица 3.2
Базисные темпы роста за полугодие, %
| Месяц | Среднемесячная заработная плата | Стоимость набора продуктов питания | Коэффициенты опережения |
| Январь Февраль Март Апрель Май Июнь | 100 104,5 113,8 114,0 119,0 127,9 | 100 103,4 105,5 107,0 108,6 111,0 | – 101 108 107 110 115 |
Коэффициенты опережения свидетельствуют о более высоких темпах роста заработной платы по сравнению с ростом цен на продукты питания.
Пример 3.3. Имеются следующие данные о динамике производства продукции предприятием за 2010 – 2014 гг., млн. руб.:
| 2010 | 2011 | 2012 | 2013 | 2014 |
| 2040 | 2130 | 2220 | 2265 | 2360 |
Определить среднегодовое производство продукции за 2010 – 2014 гг.
Решение. Для интервального ряда динамики средний уровень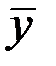 
исчисляется по формуле простой средней арифметической:
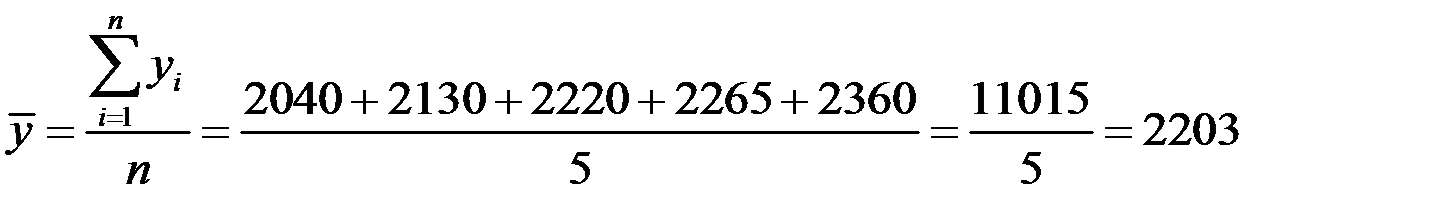млн. руб.,
где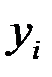 
– уровни ряда.
Пример 3.4. Имеются следующие данные об остатках сырья и материалов на складе предприятия, млн. руб.: на 01.01.14: 400; на 01.02.14: 455; на 01.03.14: 465; на 01.04.14: 460. Определить среднемесячный остаток сырья и материалов на складе предприятия за первый квартал года.
Решение. По условию задачи имеем моментный ряд динамики с равными интервалами, поэтому средний уровень ряда будет исчислен по формуле средней хронологической:
.
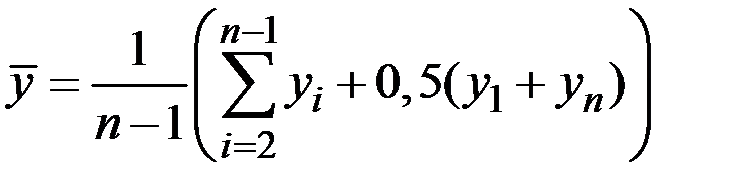Получаем
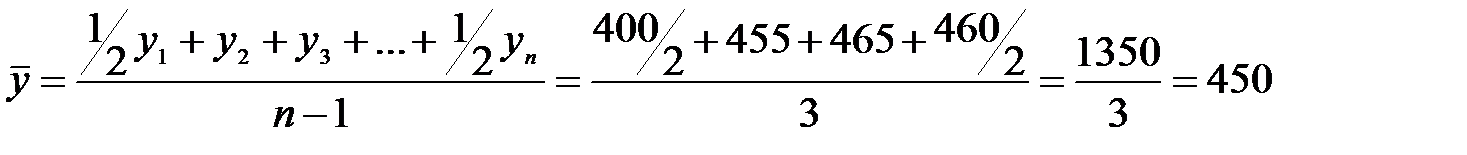млн. руб.
Пример 3.5. Имеются следующие данные о товарных запасах розничного торгового предприятия, млн. руб.: на 01.01.14: 61,1; на 01.05.14: 57,5; на 01.08.14: 51,3; на 01.01.15: 74,7. Исчислить среднемесячный товарный запас розничного торгового предприятия за 2014 г.
Решение. Средний уровень товарных запасов за год для моментного ряда динамики с неравными интервалами исчислим по формуле
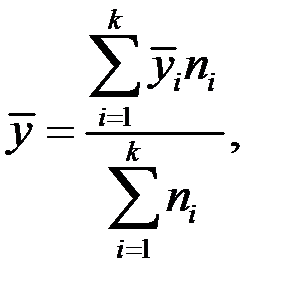
где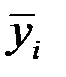 
– средние уровни интервала между датами;
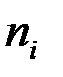– число месяцев между моментами времени.
Так, средний уровень товарных запасов за периоды: с 01.01 по 01.05:
;
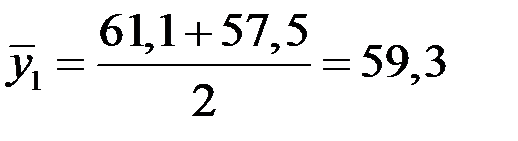с 01.05 по 01.08: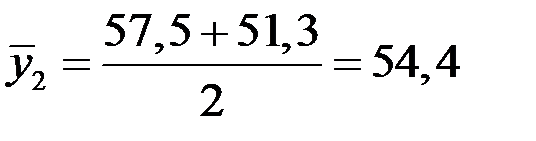 
и т.д.
Число месяцев между моментами времени равно 4, 3, 5.
Следовательно, средний уровень товарных запасов за год составит
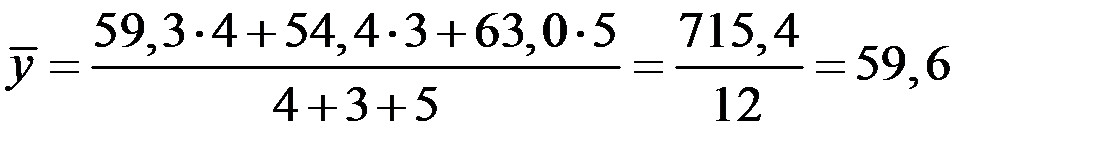млн. руб.
Пример 3.6. Имеются следующие данные о производстве продукции предприятия за 2009 – 2014 гг. (в сопоставимых ценах), млн. руб.:
| 2009 | 2010 | 2011 | 2012 | 2013 | 2014 |
| 80 | 84 | 89 | 95 | 101 | 108 |
Определить аналитические (абсолютные приросты; темпы роста; абсолютное значение одного процента прироста) и средние обобщающие показатели этого ряда динамики.
Решение. Абсолютный прирост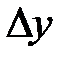 
– это разность между последующим уровнем ряда и предыдущим (или базисным).
Так, в 2010 г. цепной прирост продукции был равен:
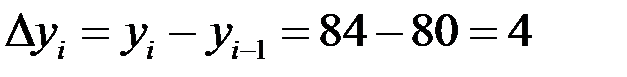млн. руб.; в 2011 г. 89 – 84 = 5 млн. руб.
Аналогично исчисляются абсолютные приросты за любой год.
Абсолютный прирост базисный: .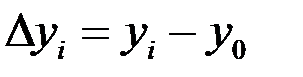
В 2010 г.: 84 – 80 = 4 млн. руб.;
в 2011 г.: 89 – 80 = 9 млн. руб. и т.д. (табл. 3.3).
Таблица 3.3
Динамика производства продукции предприятия за 2009 – 2014 гг.
|
Год
| Продук– ция в сопоста– вимых ценах, млн. руб. | Абсолютные приросты млн. руб. | Темпы роста, % | Темпы прироста, % | Абсолют–ное значение 1% прироста, млн.руб. | |||
| цепные (ежегодные) | базис–ные (к 2009 г.) | цепные (ежегод–ные) | базис–ные (к 2009 г.) | цепные (ежегодные) | базис–ные (к 2009 г.) | |||
| 2009 2010 2011 2012 2013 2014 | 80 84 89 95 101 108 | – 4 5 6 6 7 | – 4 9 15 21 28 | – 105,0 106,0 106,7 106,3 106,9 | 100 105,0 111,2 118,7 126,2 135,0 | – 5,0 6,0 6,7 6,3 6,9 | – 5,0 11,2 18,7 26,2 35,0 | – 0,8 0,84 0,89 0,95 1,01 |
Средний абсолютный прирост исчисляется двумя способами:
а) как средняя арифметическая простая годовых (цепных) приростов
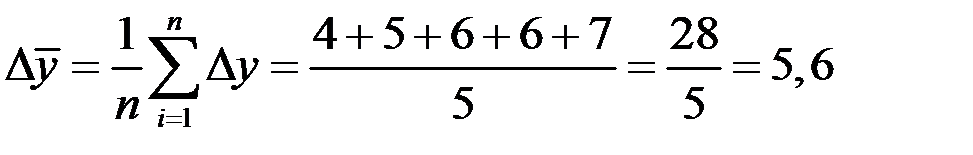млн. руб.;
б) как отношение базисного прироста к числу периодов
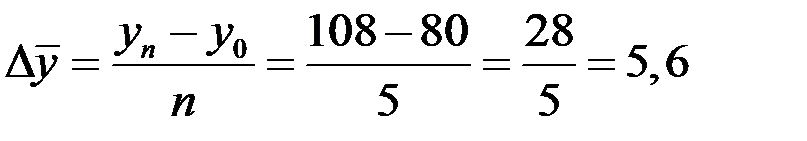млн. руб.
Цепные темпы роста составили:
в 2010 г. по сравнению с 2009 г.
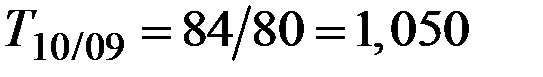(105%);
в 2011 г. по сравнению с 2010 г.
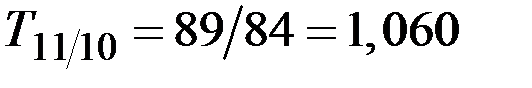(106%) и т.д.
Базисные темпы роста за эти же периоды равны:
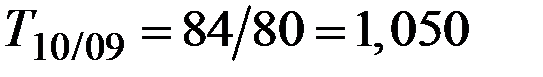(105%);
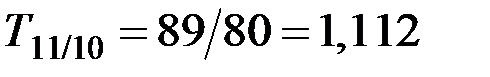(106%) и т.д.
Между цепными и базисными темпами роста имеется взаимосвязь: произведение соответствующих цепных темпов роста равно базисному.
Зная базисные темпы, можно исчислить цепные делением каждого последующего базисного темпа роста на каждый предыдущий.
Темп прироста определяют двумя способами:
а) как отношение абсолютного прироста к предыдущему уровню:
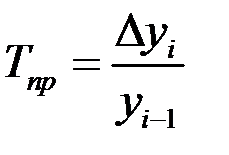– цепной,
или к базисному уровню
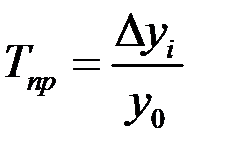– базисный.
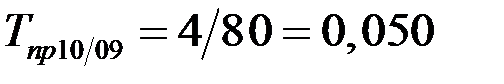(5,0%); 
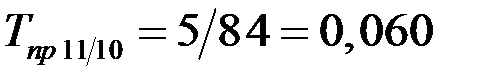(6,0 %);
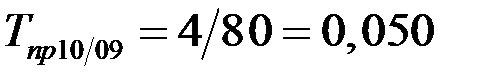(5,0%); 
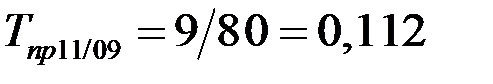(11,2 %) и т.д.;
б) как разность между темпами роста и единицей, если темпы роста выражены в коэффициентах:
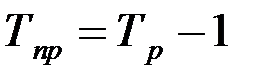
или как разность между темпами роста и 100%, если темпы роста выражены в процентах:
%.
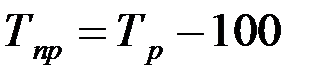Получаем:
,
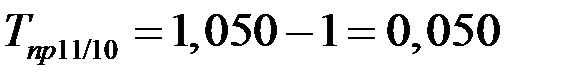или
105% – 100% = 5,0%, и т.д.
Абсолютные приросты одного процента прироста (А1%) равно отношению абсолютного прироста цепного к темпу прироста цепному.
2010 г.: А1% =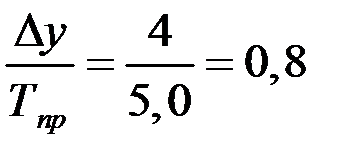 
млн. руб., или 800 тыс. руб.;
2011 г.: А1% = 5/5,9 = 0,84 млн. руб., или 840 тыс. руб., и т.д.
Этот показатель может быть исчислен иначе: как одна сотая часть предыдущего уровня.
Например, в 2010 г. по сравнению с 2009 г. абсолютное содержание 1% прироста составило:
А1% =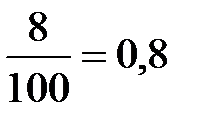 
млн. руб., или 800 тыс. руб.
Расчёт среднего абсолютного значения одного процента прироста за несколько лет производится по формуле
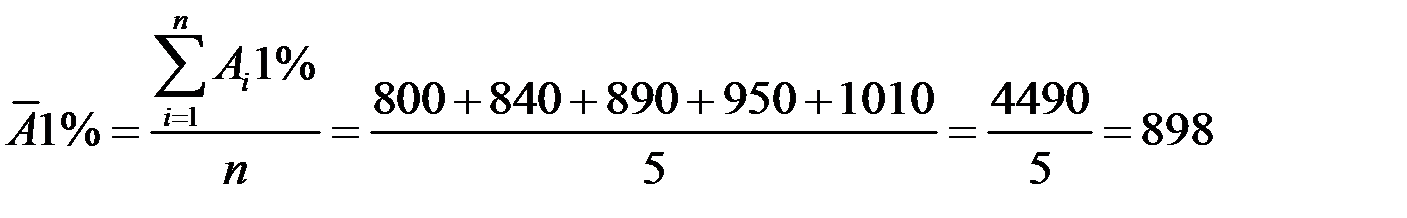тыс. руб.
Все результаты расчётов приведены в табл. 3.3.
Пример 3.7. По данным примера 3.6 исчислить среднегодовой темп роста и прироста производства продукции за исследуемый период.
Решение. Среднегодовой темп роста исчисляется по формуле средней геометрической из цепных коэффициентов роста:
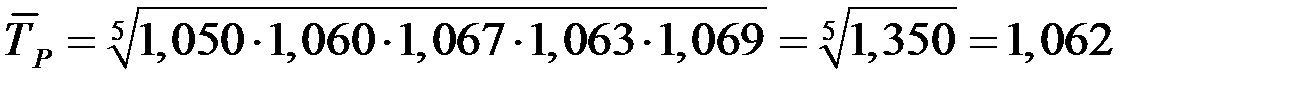(106,2%).
Среднегодовой темп роста может быть исчислен из отношения конечного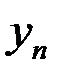 
и начального 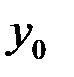по формуле
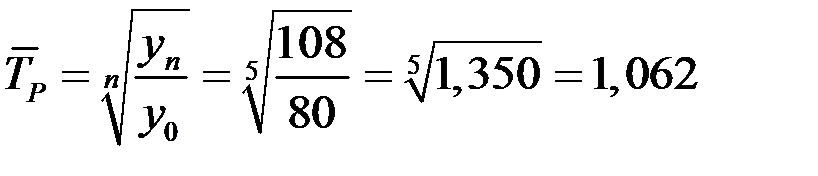(106,2%).
Среднегодовой темп роста за 2009 – 2014 гг. равен 106,2%.
Среднегодовой темп прироста исчисляется следующим образом:
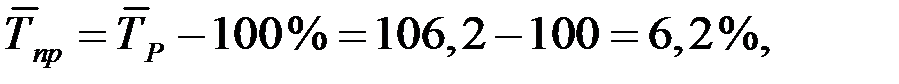или
.
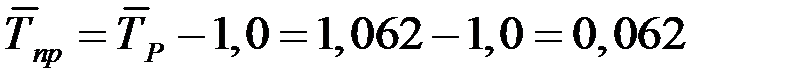Таким образом, производство продукции в период 2009 – 2014 гг. увеличивалось за год в среднем на 6,2%.
Обобщим понятия абсолютных приростов, темпов роста, и темпов прироста для непрерывного и дискретного времени.
Если рассматривается зависящая от времени величина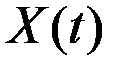 
, то абсолютный прирост этой величины от момента 
до момента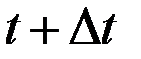 
равен
,
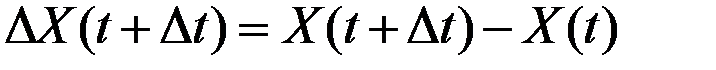дискретный темп роста равен величине (индексу)
,
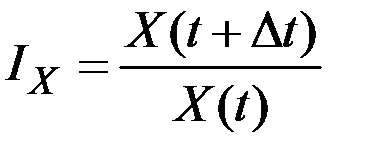дискретный темп прироста равен величине
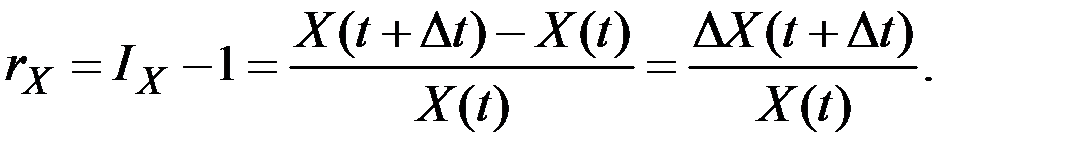
Непрерывный темп роста величины 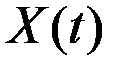равен значению
.
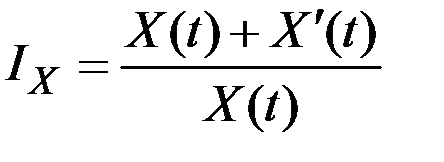Непрерывный темп прироста величины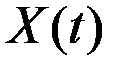
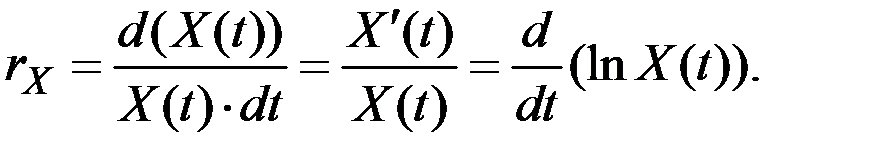
Если темп прироста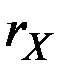 
дискретен и неизменен во времени, то динамика показателя 
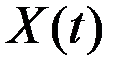может быть описана в виде зависимости
.
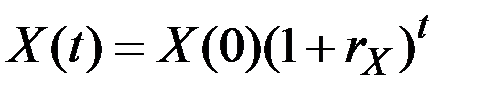Если величина 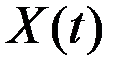есть непрерывная функция времени, то её рост с непрерывным темпом прироста 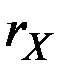записывается в виде
,
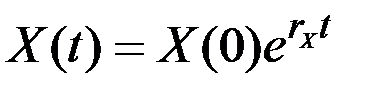где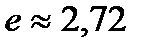 
– основание натуральных логарифмов,
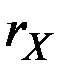– непрерывный темп прироста.
При росте величины 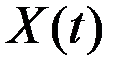с непрерывным темпом прироста 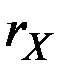дискретный темп роста за один такт времени 
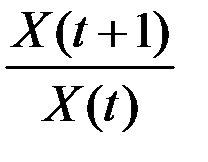равен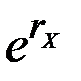 
, что при малых 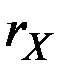близко к (1+ 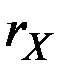), то есть к темпу роста при дискретном темпе прироста .
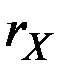Исследуем темпы прироста суммы и произведения двух показателей с различными темпами прироста.
1. Пусть показатель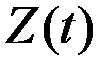 
есть сумма показателе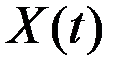й и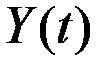 
, растущих соответственно, с постоянными непрерывными темпам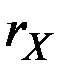и и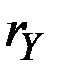 
, причём 
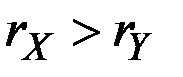. Тогда
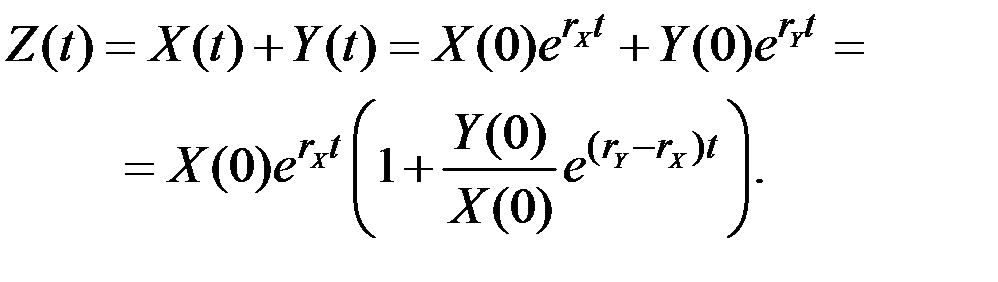
Поскольку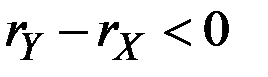 
, то величина в скобках стремится к единице при 
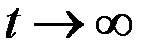, и темп прироста суммы приближается к темпу быстрее растущего составляющего, то есть к 
.
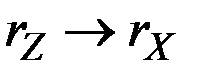2. Сумма показателе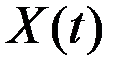й и 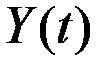, растущих с постоянными дискретными темпам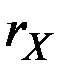и и 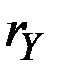, причём 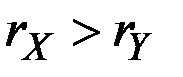описывается зависимостью
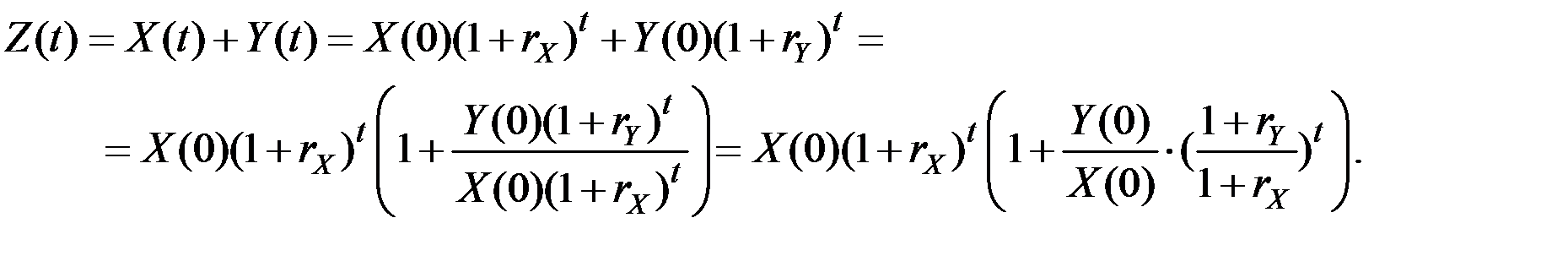
Поскольку 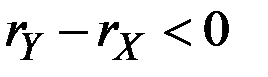, то величина в скобках стремится к единице при 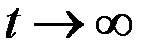, и темп прироста суммы приближается к темпу быстрее растущего составляющего, то есть к .
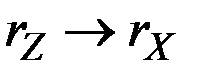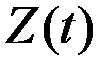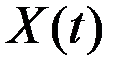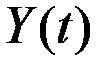3. Пусть величина есть произведение показателей и , растущих с постоянными непрерывными темпам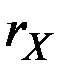и и 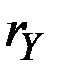. Тогда:
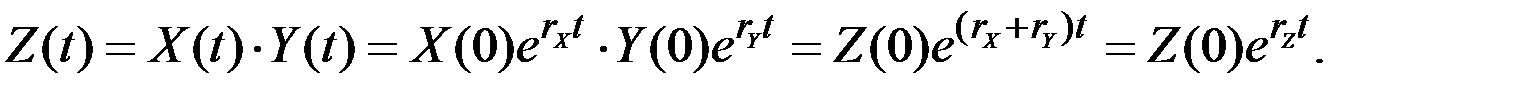
Здесь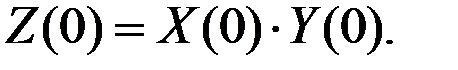 
В этом случае темп прироста произведения равен сумме темпов прироста сомножителей: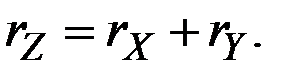 
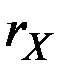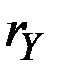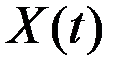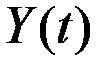4. Если и – дискретные темпы прироста и , то
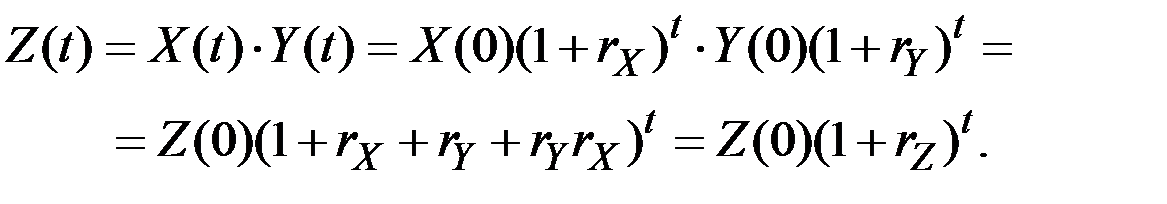
Здесь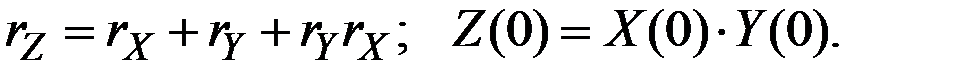 
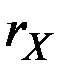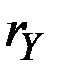При малых и величина 
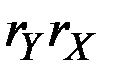пренебрежимо мала, и темп прироста произведения приближённо равен сумме темпов прироста сомножителей. Если же произведение 
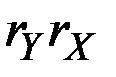значительно, то темп прироста произведения показателей не может приближённо считаться равным сумме темпов прироста сомножителей, поскольку существенно её превышает.
Индексный метод
Индекс – это относительный статистический показатель (индикатор), который обобщает относительное изменение одной переменной или группы переменных.
Индексы полезны, когда значения, лежащие в основе расчёта, очень велики и их абсолютные изменения трудно понять (в частности, при анализе валового национального продукта страны).
С другой стороны, индексы применяются для обобщения совокупного изменения в группе составляющих (показателей), каждая из которых меняется в разной степени.
Например, индекс розничных цен обобщает изменение цен набора (корзины) товаров и услуг, приобретаемых "типичным" домашним хозяйством.
Биржевые индексы обобщают изменение цен некоторой совокупности финансовых инструментов, зарегистрированных на той или иной бирже.
Различают индивидуальные и сводные (общие) индексы.
Индивидуальный индекс представляет собой обычную относительную величину динамики показателя.
Индивидуальный индекс часто обозначают буквой I с подстрочным указанием индексируемого показателя. Индексируемым называют показатель, изменение которого характеризует индекс.
Так, например, для характеристики выполнения планового задания по производству отдельных видов продукции рассчитывают индивидуальные индексы физического объёма продукции по формуле
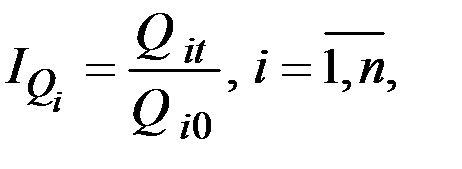
где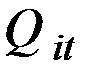 
, 
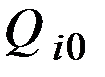– объём производства (индексируемая величина) какого–то конкретного 
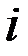–го вида продукции в натуральном выражении соответственно в отчётном (текущем) и базисном периодах.
Сводный индекс (агрегатный) характеризует изменение явления, состоящего из разнородных непосредственно не суммируемых элементов.
Здесь элементы суммируют с некоторыми весами с учётом их смысла и возможности объективной интерпретации.
Например, с помощью сводных индексов характеризуют изменение объёма выпуска продукции на мебельной фабрике, изготавливающей различную продукцию: столы, стулья, шкафы, диваны, или изменение среднего уровня цен на различные продукты питания или услуги в текущем периоде по сравнению с базисным и т.п.
Умножив объём различных видов изделий на их себестоимость, получаем стоимостную форму изделий, которая позволяет их суммировать и сопоставлять.
При этом, чтобы индекс отражал изменение только индексируемой величины, веса индексов берут на одном уровне.
Если в качестве веса используют объёмные показатели (продукции, численности), их берут на уровне текущего периода, если качественные показатели (цена, себестоимость, затраты времени на единицу продукции), то их принимают на уровне базисного периода.
Индекс Ласпейреса использует веса базисного периода.
Индекс Пааше использует веса текущего периода.
Индекс Фишера – средняя гармоническая из индексов Ласпейреса и Пааше (удовлетворяется требование независимости индекса от выбора базы сравнения):
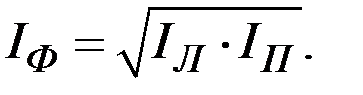
На практике широко применяют индексы физического объёма продукции, индекс себестоимости, индекс затрат, индекс реализованной продукции, индекс цен, индекс товарооборота, индекс производительности труда, индекс удельного расхода материалов, индекс сбыта и др.
Обозначим:
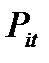– текущая цена i–го товара (в отчётный период) t;
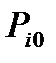– цена i–го товара в базовый (базисный) период;
, 
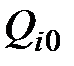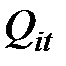– количество i–го товара, произведённого в базовый период и текущий момент времени t, соответственно;
, 
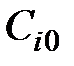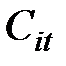– себестоимость i–го товара (каждого вида изделий) в базовый и текущий (отчётный) период времени t, соответственно;
, 
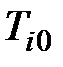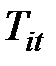– затраты времени на производство единицы продукции соответственно в базисном и текущем периодах.
Тогда сводный индекс физического объёма продукции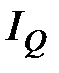 
в общем виде определяется по формуле
.
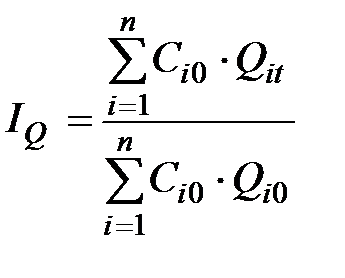Сводный индекс себестоимости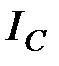 
характеризует, как в среднем изменяется себестоимость продукции различных видов в целом по анализируемой совокупности, и определяется по формуле
.
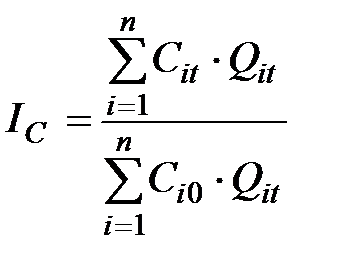Сводный индекс затрат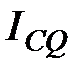 
характеризует, как изменились затраты по производству продукции различных видов в целом по анализируемой совокупности, и определяется по формуле
.
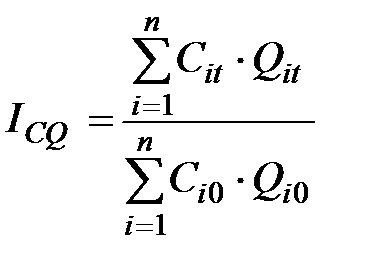Сводный индекс цен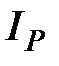 
характеризует, как изменились в среднем цены на различные виды продукции по анализируемой совокупности, и определяется по формуле
.
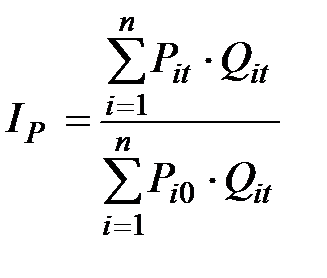Сводный индекс товарооборота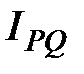 
определяется по формуле
.
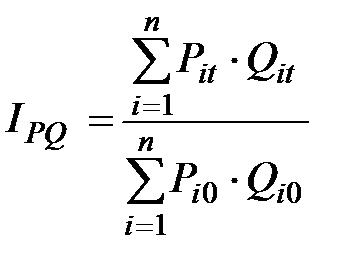Сводный индекс трудоёмкости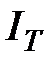 
характеризует, как в среднем изменились затраты времени на единицу продукции в связи с ростом производительности труда, и определяется по формуле
.
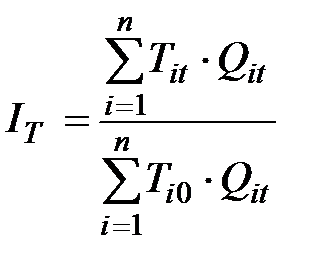Сводный индекс производительности труда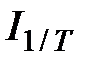 
характеризует изменение производительности труда, является показателем, обратным индексу трудоёмкости, и определяется по формуле
.
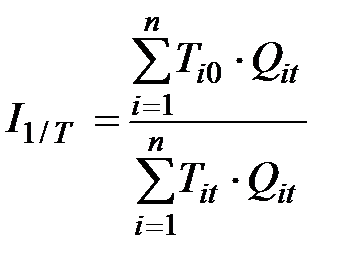Сводный индекс массы отработанного времени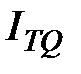 
:
,
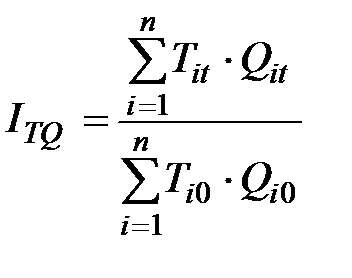где выражения в числителе и знаменателе – это время, затраченное на производство всей продукции соответственно в текущем и базисном периодах.
Расчёт индексов может быть выполнен в агрегатной форме и в форме средних индивидуальных индексов (среднеарифметического взвешенного и среднегармонического). Все вышеперечисленные индексы рассчитаны как агрегатные индексы.
Выбор формы расчёта индексов зависит от наличия исходных данных. Если известны значения индексируемого показателя и веса в текущем и базисном периодах, то пользуются агрегатной формулой индексов.
Если отсутствуют значения индексируемого показателя или веса в текущем или базисном периодах, но известны изменения индексируемого показателя или веса по отдельным единицам анализируемой совокупности, то пользуются формулой средних индексов.
Пример 3.8. Известен плановый размер затрат по выпуску продукции на предприятии (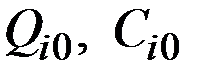 
) и задание по росту выпуска продукции отдельных видов 
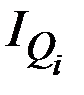. Необходимо определить индекс физического объёма продукции .
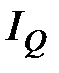Решение. Индекс физического объёма продукции определяется по формуле
.
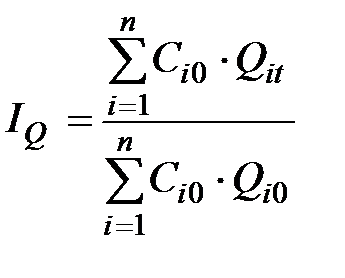Неизвестен фактический выпуск продукции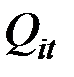 
, но задан рост каждого вида продукции 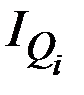, который определяется по формуле
.
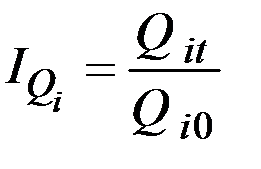Отсюда определяем
.
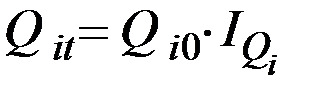Подставляем найденную величину в исходную формулу:
.
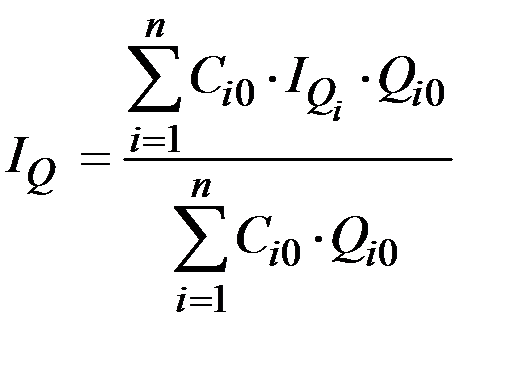Это и есть средняя арифметическая взвешенная индекса физического объёма (среднеарифметический индекс).
Пример 3.9. Известны размер товарооборота в отчётном периоде и изменение цен в отчётном периоде относительно планового по отдельным видам изделий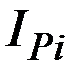 
. Необходимо определить, как в среднем изменились цены по всем видам изделий, т.е. сводный индекс цен 
.
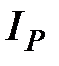Решение. Сводный индекс цен Пааше 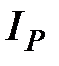определяется по формуле:
.
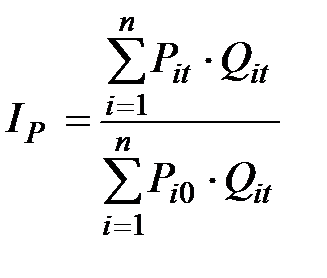У нас известен товарооборот в отчётный период, а товарооборот в ценах планового периода не известен, но заданы индивидуальные индексы цен по каждому виду изделий, которые определяются по формуле
.
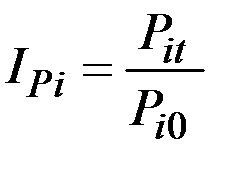Отсюда можно определить цены планового периода
.
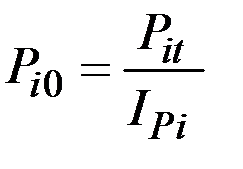Подставляем их в исходную формулу:
.
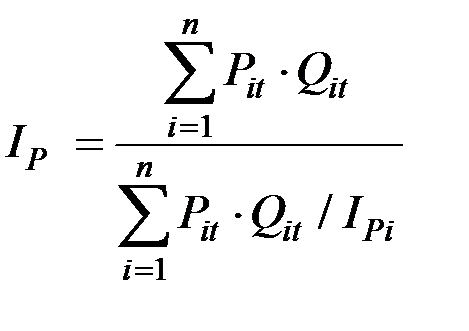Это средняя гармоническая индекса цен (среднегармонический индекс Пааше).
Индексы подчиняются той же взаимосвязи, что и характеризуемые ими показатели. Например, затраты определяют как произведение себестоимости продукции на объём продукции.
Тогда и индекс затрат равен произведению индексов себестоимости и физического объёма продукций:
.
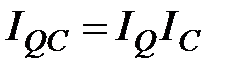Пользуясь взаимосвязью индексов, можно по величине двух из них определить величину третьего.
Индексы широко используются в факторном анализе для выявления меры влияния факторных показателей на средний уровень определяемого или результативного показателя.
Пример 3.10. Известно, что по плану на предприятии ожидается рост выпуска физического объёма продукции на 18%, и снижение себестоимости изделий в среднем на 3%. Необходимо определить изменение затрат на заданный объём работ.
Решение. Пользуясь взаимосвязью индексов затрат, физического объёма и себестоимости, определяем изменение затрат
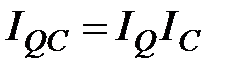= 0,97·1,18 = 1,1448 или 114,46%.
Индекс затрат достигает 114,46%, т.е. затраты вырастут на 14,46%.
Часто динамику показателя характеризуют несколькими индексами: 1) переменного состава; 2) постоянного состава; 3) структурных сдвигов.
Пример 3.11. Известны объёмы перевозок каждого вида (рода) груза и их себестоимость в текущем и базисном периодах табл. 3.4. Необходимо определить: 1) индекс средней себестоимости перевозок (индекс переменного состава); 2) на сколько процентов изменение среднего уровня себестоимости перевозок обусловлено изменением самой себестоимости как таковой (индекс постоянного состава); 3) на сколько процентов изменение среднего уровня себестоимости перевозок обусловлено изменением структуры (объёмов) перевозок.
Таблица 3.4
Динамика объёма и себестоимости перевозок грузов
| Вид груза | Объём перевозок, тыс. тонн–км. | Себестоимость перевозок, руб./тонн–км | ||
| Базисный период | Отчётный период | Базисный период | Отчётный период | |
| Оборудование | 14400 | 17500 | 4,0 | 5,0 |
| Продукты питания | 2000 | 2500 | 3,0 | 3,5 |
| Стройматериалы | 600 | 1000 | 1,5 | 2,0 |
Решение. 1. Изменение среднего уровня себестоимости определяется как отношение среднего уровня себестоимости перевозок по всем грузам в отчётном и базисном периодах:
.
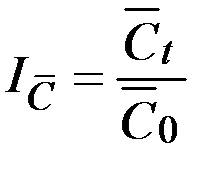Средняя себестоимость, в свою очередь, определяется как отношение общих затрат на перевозки (производство) к объёму продукции:
;
.
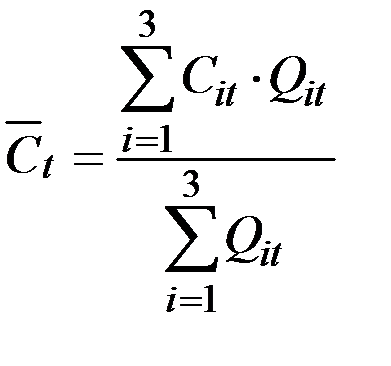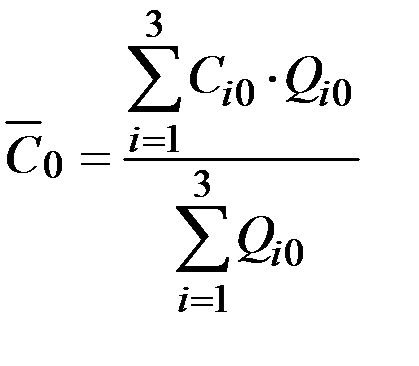Сопоставляя средние уровни себестоимости отчётного и планового периодов наблюдаем изменение двух факторов: себестоимости и объёма перевозок:
= 
: 
=
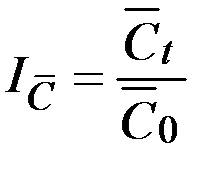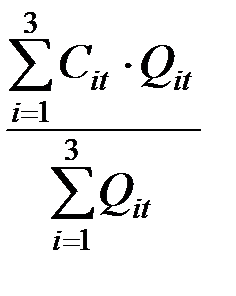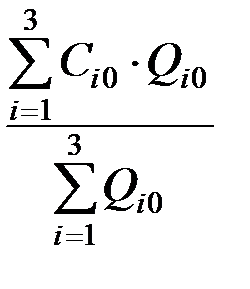Средняя себестоимость перевозок всех грузов под влиянием роста себестоимости и объёма перевозок возросла на 23,31%.
Этот индекс называется индексом переменного состава.
2. Чтобы определить влияние изменения себестоимости перевозок отдельных грузов на среднюю себестоимость перевозок всех грузов, надо исключить влияние структуры перевозок (объёмов) на её величину.
Для этого объёмы перевозок берут на одном (отчётном) уровне:
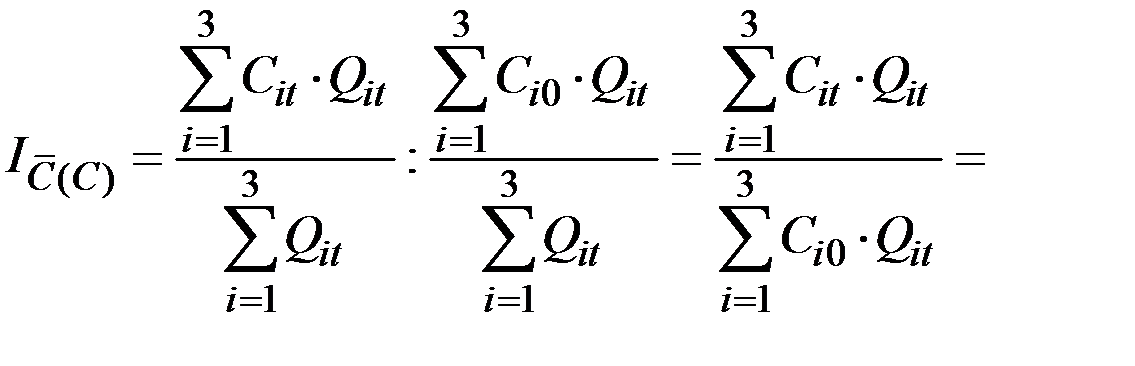
За счёт роста себестоимости перевозок отдельных грузов в среднем себестоимость выросла на 24,38%.
Этот индекс называют индексом постоянного состава.
Он отражает влияние только индексируемого показателя.
По существу это тот же сводный индекс себестоимости.
3. Для оценки влияния изменения объёмов перевозок по определённым грузам, т.е. влияния структуры перевозок на средний уровень себестоимости грузов, необходимо нивелировать (устранить, элиминировать) влияние изменения себестоимости перевозок отдельных грузов на её средний уровень. С этой целью себестоимость перевозки отдельных грузов берём на одном уровне – плановом (базовом), поскольку это качественный показатель:
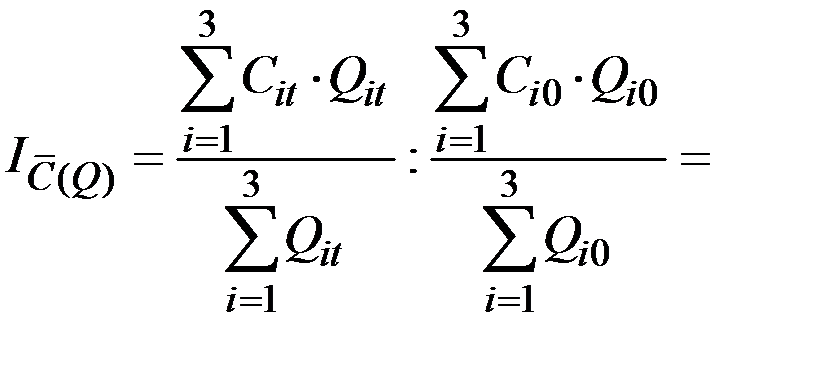
Как показывает расчёт, за счёт изменения структуры перевозок средняя себестоимость перевозок всех грузов снизилась на 0,85%.
Этот индекс называют индексом структурных сдвигов.
Он отражает влияние структуры объёма работ на средний уровень индексируемого показателя (себестоимости 1 тн/км).
Правильность выполнения расчётов можно проверить через взаимосвязь индексов:
.
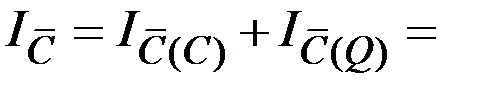
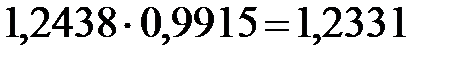Дата: 2019-03-05, просмотров: 692.
