Все переменные любой модели в зависимости от конечных прикладных целей её использования принято делить на экзогенные, эндогенные и предопределённые.

Экзогенные – это переменные, которые входят в модель, но рассматриваются как определённые независимо от моделируемого явления.

Экзогенные переменные заданы как бы «извне», автономно.

В определённой степени это управляемые (планируемые) независимые (объясняющие) переменные.

Эндогенные – это переменные, которые определяются только явлением, для которого строится модель.

Значения этих переменных формируются в процессе и внутри функционирования анализируемой системы (в существенной мере под воздействием экзогенных переменных и во взаимодействии друг с другом).

В модели они являются предметом объяснения, и в этом смысле их иногда называют зависимыми (объясняемыми) переменными.

Предопределённые – это переменные, выступающие в системе в роли факторов (аргументов) или объясняющих переменных.

Множество предопределённых переменных формируется из всех экзогенных переменных (которые могут быть «привязаны» к прошлым, текущему или будущим моментам времени) и так называемых лаговых эндогенных переменных, т.е. таких эндогенных переменных, значения которых входят в уравнения анализируемой системы измеренными в прошлые (по отношению к текущему) моменты времени, а следовательно, являются уже известными, заданными.

Модель и служит для объяснения поведения эндогенных переменных в зависимости от значений экзогенных и лаговых эндогенных переменных.

Между двумя переменными может существовать функциональная связь, когда каждому значению величины Х соответствует определённое значение другой величины .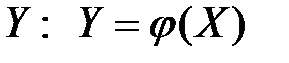

Функциональные связи характеризуются полным соответствием между изменением факторных признаков и изменением результативной величины, то есть каждому конкретному набору значений факторов соответствует определённое значение результативного признака.

Например, при повременной оплате труда размер зарплаты функционально зависит от количества отработанного времени.

Стохастическая связь состоит в том, что одна величина (показатель) реагирует на изменение другой изменением своего закона распределения (рис. 5.1).

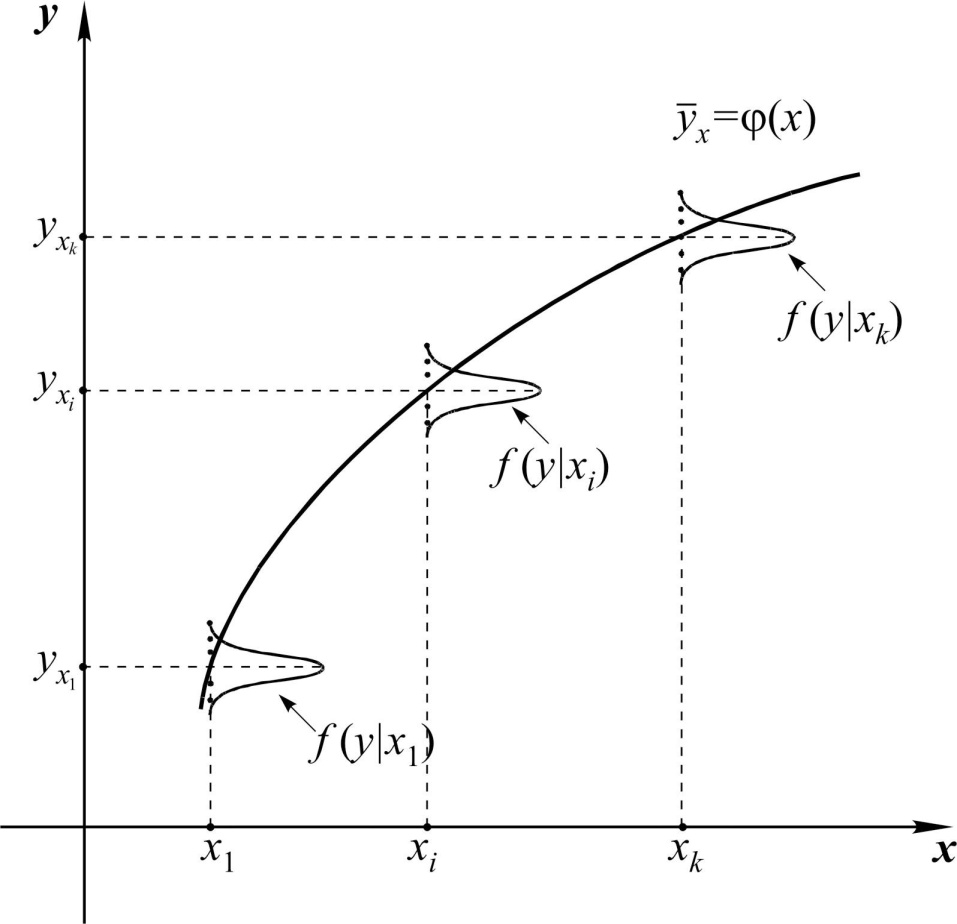
Рис. 5.1. Построение стохастической связи двух переменных

Частный случай стохастической связи – статистическая связь (корреляционная), когда условное математическое ожидание одной величины реагирует на изменение другой величины.

Регрессионный анализ выполняется в 3 этапа (решает задачи).

1. Выбор формы связи между переменными, т.е. модели регрессии.

2. Оценка неизвестных параметров выбранной модели.

3. Оценка качества полученной модели и проверка соответствующих статистических гипотез о регрессии.

1. Форма связи между переменными, т.е. вид уравнения регрессии, выбирается исследователем либо из каких–то теоретических предпосылок, либо из соображений удобства работы с этой формулой (зависимостью), либо из вида и анализа графического изображения имеющихся статистических данных, либо из совокупности возможных математических моделей, выбрав подходящую с помощью соответствующего критерия приближения к имеющимся данным, либо из других каких–либо соображений (предпочтений).

2. Для оценки параметров регрессионного уравнения наиболее часто используют метод наименьших квадратов (МНК).

Основной принцип этого метода заключается в том, чтобы так определить неизвестные параметры модели, чтобы сумма квадратов отклонений имеющихся данных от выбранной модели (уравнения) регрессии была бы минимальной:

.

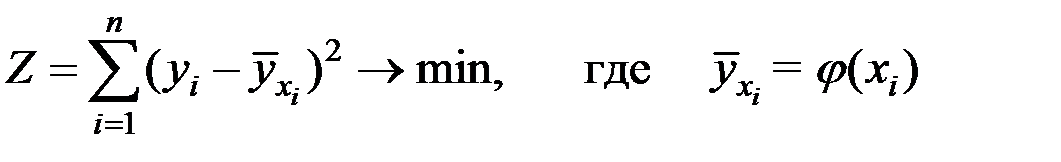МНК удобен тем, что производная от этого критерия даёт линейное уравнение относительно неизвестных параметров модели.

После получения уравнения регрессии производится оценка его качества.

3. Для оценки качества регрессионных моделей целесообразно:

1) вычислить и оценить значимость соответствующего параметра корреляционного анализа (линейного коэффициента корреляции, коэффициента множественной корреляции, индекса корреляции и др.);

2) проверить адекватность (значимость) всей модели регрессии;

3) оценить точность модели, т.е. вычислить среднее квадратическое отклонение остатков ;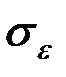

4) проверить значимость каждого параметра модели регрессии;

5) определить доверительные границы всей модели регрессии;

6) определить доверительные границы (интервальные оценки) каждого параметра модели регрессии.

Качество модели обычно оценивается по адекватности и точности на основе анализа остатков регрессии, т.е. разности наблюдаемых и расчётных значений зависимой переменной:

.

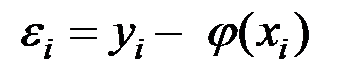Расчётные значения 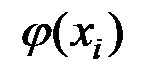 получаются путём подстановки в модель фактических значений всех включённых факторов.

Анализ остатков позволяет получить представление, насколько хорошо подобрана сама модель и насколько правильно выбран метод оценки коэффициентов.

Согласно общим предположениям регрессионного анализа остатки должны вести себя как независимые (почти независимые) одинаково распределённые случайные величины.

В классических методах регрессионного анализа предполагается также нормальный закон распределения остатков.

Независимость остатков проверяется с помощью критерия Дарбина – Уотсона.

Исследование остатков полезно начинать с изучения их графика.

График остатков может показать наличие какой–то зависимости, не учтённой в модели.

При подборе простой линейной зависимости между Y и X график остатков может показать необходимость перехода к нелинейной модели (квадратичной, полиномиальной, экспоненциальной) или включения в модель периодических компонент.

График остатков хорошо показывает и резко отклоняющиеся от модели наблюдения – выбросы.

Подобным аномальным наблюдениям надо уделять пристальное внимание, так как их присутствие может грубо искажать значения оценок.

Устранение эффектов выбросов может проводиться либо с помощью удаления этих точек из анализируемых данных (эта процедура называется цензурированием), либо с помощью применения методов оценивания параметров, устойчивых к подобным грубым отклонениям.

Оценка качества регрессионных моделей часто производится с использованием коэффициента детерминации R² (квадрат коэффициента множественной корреляции, индекса корреляции, линейного коэффициента корреляции).

Коэффициент детерминации показывает долю вариации (дисперсии) результативного признака, находящегося под воздействием изучаемых факторов, т.е. определяет, какая доля дисперсии признака Y учтена в модели и обусловлена влиянием на него других факторов.

Чем ближе R² к 1, тем лучше качество модели.

Оценить значимость всего уравнения регрессии – это означает установить, соответствует ли математическая модель, выражающая зависимость между Y и X, фактическим данным и достаточно ли включённых в уравнение объясняющих переменных X для описания зависимой переменной Y.

Для проверки значимости модели регрессии используется F–критерий Фишера с использованием коэффициента детерминации:

.

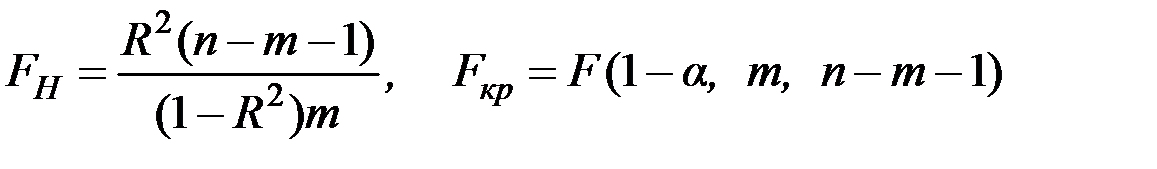Если расчётное значение 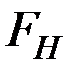  больше табличного (критического) значения  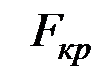 с v₁= m  и  v₂ = (п – m – 1) степенями свободы (где m – количество независимых факторов, включённых в модель) при заданном уровне значимости 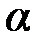, то модель считается значимой.

В качестве меры точности применяют несмещённую оценку дисперсии остаточной компоненты, которая представляет собой отношение суммы квадратов уровней остаточной компоненты к числу степеней свободы, т.е. к величине (п – m – 1), где m – количество факторов, включённых в модель.

Квадратный корень из этой величины 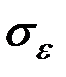 называется стандартной ошибкой оценки:

.

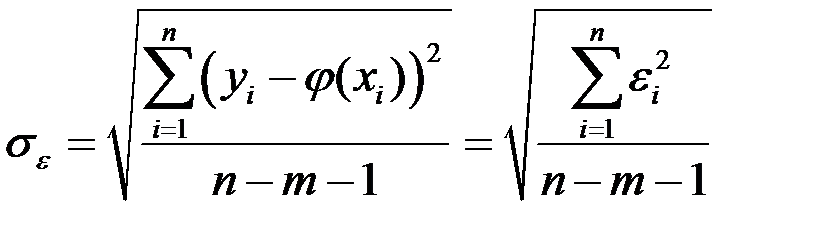где                                              

.

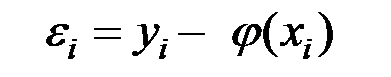Регрессионные модели могут быть использованы для прогнозирования возможных ожидаемых значений зависимой переменной.

Прогнозируемое значение переменной у_пр получается при подстановке в уравнение регрессии ожидаемой величины фактора х_пр.

Данный прогноз называется точечным.

При выборе ожидаемой величины х_пр нельзя подставлять значения независимой переменной х_пр, значительно отличающиеся от входящих в исследуемую выборку, по которой вычислено уравнение регрессии.

Вероятность реализации точечного прогноза практически равна нулю.

Поэтому рассчитывается средняя ошибка прогноза или доверительный интервал прогноза с достаточно большой вероятностью (надёжностью).

Доверительный интервал линии регрессии определяется соотношением:

.

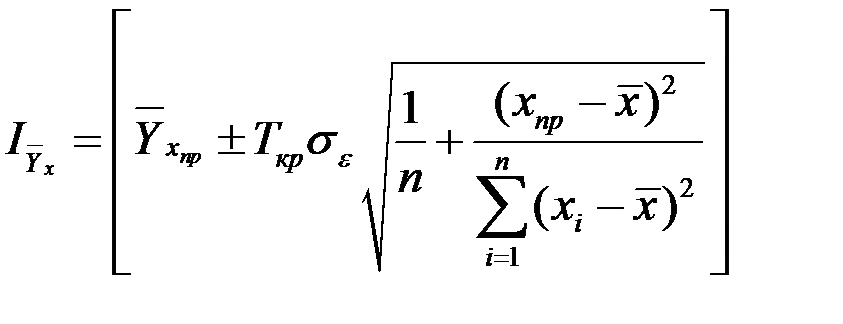Стандартная ошибка линии регрессии определяется соотношением

.

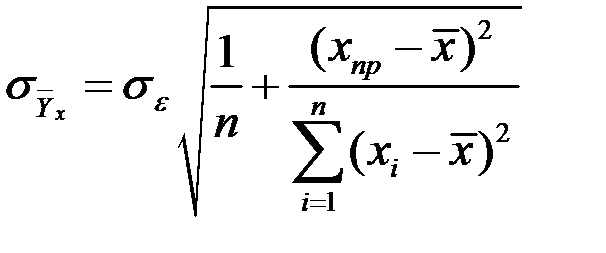Доверительный интервал для прогнозов индивидуальных значений 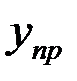 определяется из соотношения:

,

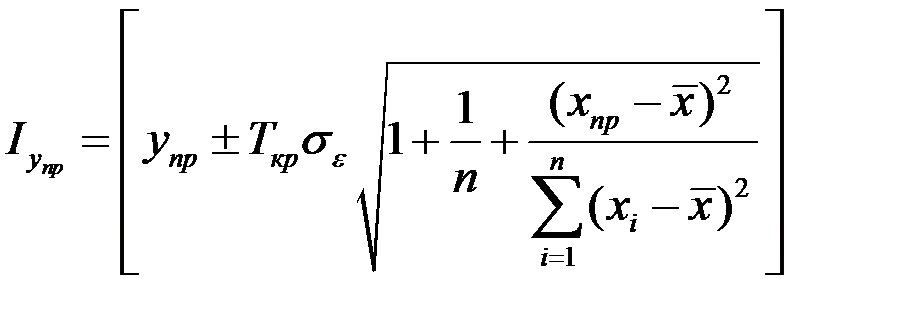где 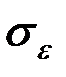 – стандартная ошибка зависимой переменной;

х = х_пр – значение фактора X, используемое для прогноза;

п – число наблюдений.

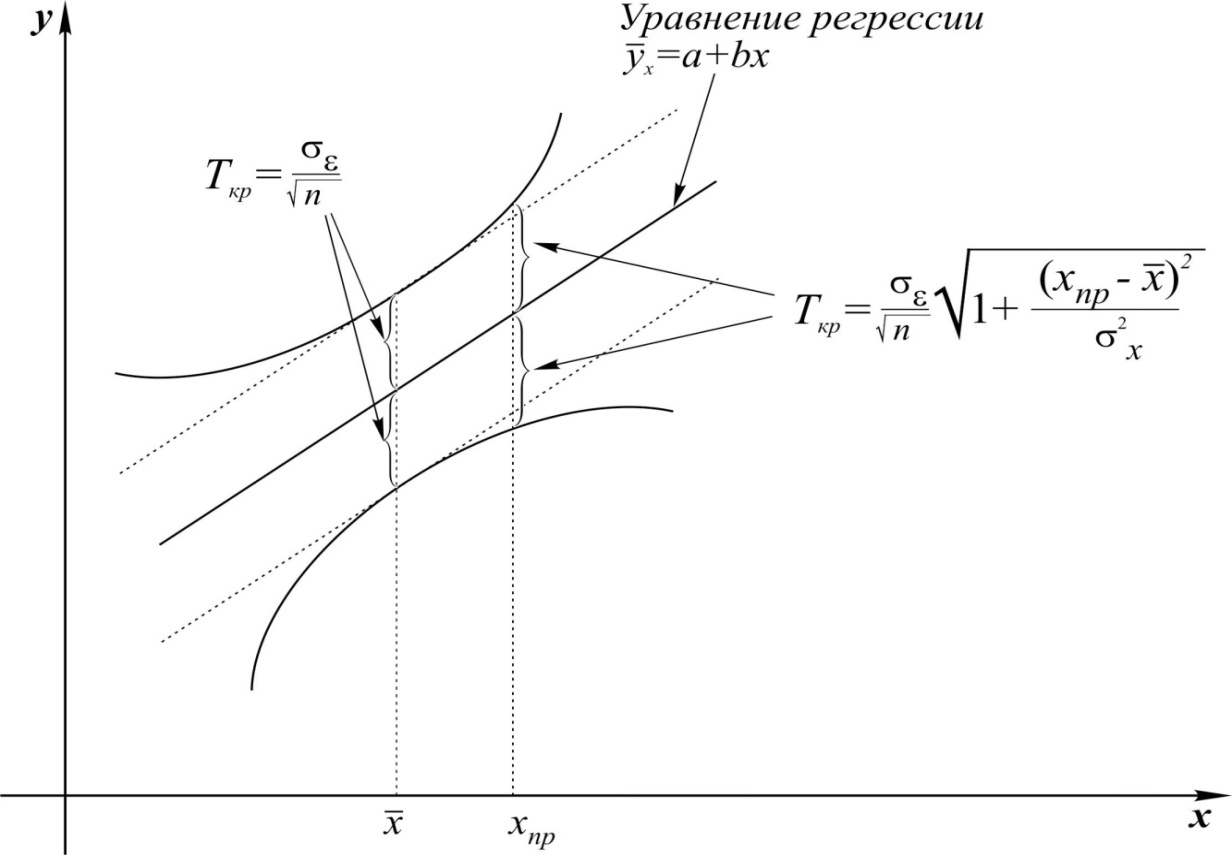
Рис. 5.2. Доверительные границы для уравнения регрессии

Расположение границ доверительного интервала показывает, что прогноз значений зависимой переменной по уравнению регрессии хорош только в случае, если значение фактора Х не выходит за пределы выборки (экстраполяция по уравнению регрессии может привести к значительным погрешностям).

Линейная парная регрессия

Под линейностью здесь имеется в виду, что переменная Y предположительно находится под влиянием переменной X в линейной зависимости:

.

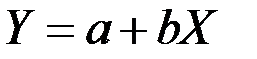Для отдельного наблюдения имеем соотношение:

,

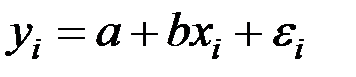где a – постоянная величина (свободный член уравнения);

b – коэффициент регрессии, определяющий наклон линии, вдоль которой рассеяны данные наблюдений. Коэффициент регрессии характеризует изменение переменной Y при изменении значения Х на единицу. Если b > 0 – переменные Х и Y положительно коррелированные, если b < 0 – отрицательно коррелированные;

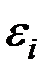 – независимая нормально распределённая СВ – остаток с нулевым математическим ожиданием и постоянной дисперсией. Она отражает тот факт, что изменение Y будет неточно описываться изменением X (присутствуют другие факторы, не учтённые в данной модели).