1. Сравнение двух дисперсий нормальных генеральных совокупностей. 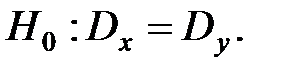
Критерий 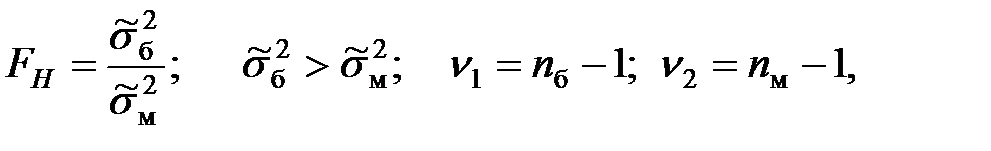
где 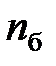 – объём выборки с большей дисперсией,
– объём выборки с большей дисперсией,
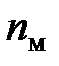 – объём выборки с меньшей дисперсией.
– объём выборки с меньшей дисперсией.
2. Сравнение выборочной дисперсии 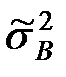 с гипотетической генеральной дисперсией
с гипотетической генеральной дисперсией 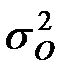 нормальной генеральной совокупности.
нормальной генеральной совокупности. 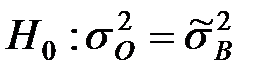 .
.
Критерий 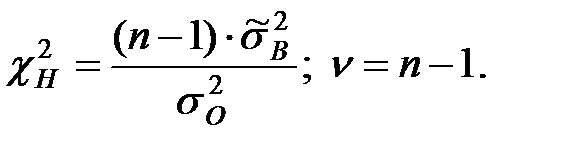
3. Сравнение двух средних генеральных совокупностей, дисперсии которых известны (большие независимые выборки n > 30, m > 30).
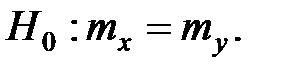
Критерий 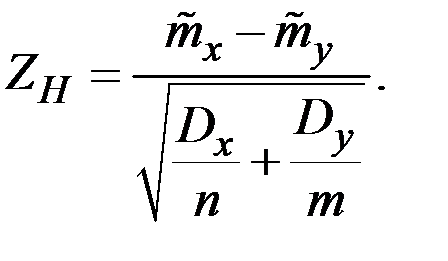
4. Сравнение двух средних нормальных генеральных совокупностей, дисперсии которых неизвестны и одинаковы (малые независимые выборки). 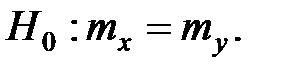
Критерий 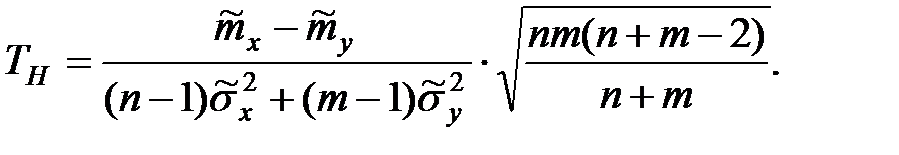
5. Сравнение выборочной средней с гипотетической генеральной средней нормальной совокупности с известной дисперсией. 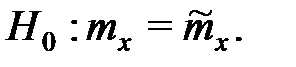
Критерий 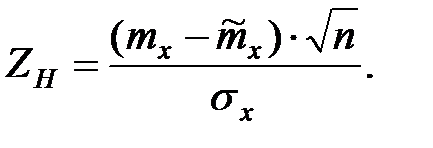
6. Сравнение выборочной средней с гипотетической генеральной средней нормальной совокупности, если дисперсия генеральной совокупности неизвестна. 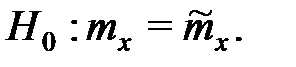
Критерий 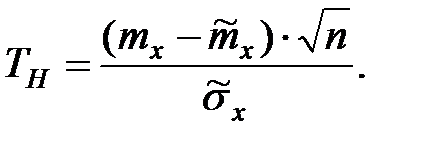
7. Сравнение двух средних нормальных генеральных совокупностей с неизвестными дисперсиями (зависимые выборки).
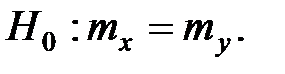
Критерий 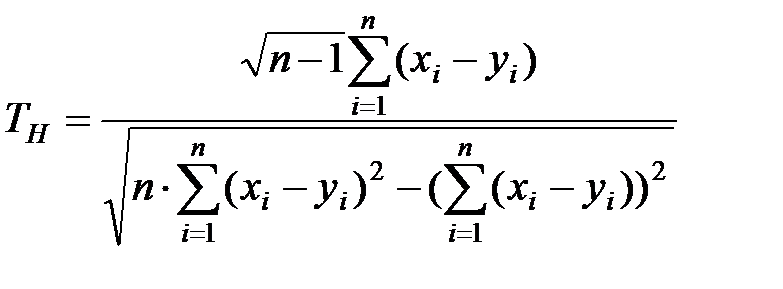 .
.
8. Сравнение наблюдаемой относительной частоты 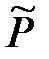 с гипотетической вероятностью появления события
с гипотетической вероятностью появления события 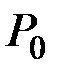 .
.
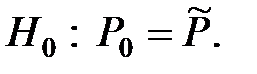
Критерий 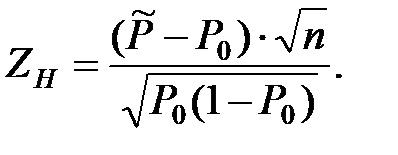
Пример 2.1. Две автоматические линии расфасовывают картофель по упаковкам. Для анализа отобрали по несколько пакетов с каждой линии и взвесили их. Получили следующие результаты (в кг):
1–я линия: 25,1; 24,6; 24,2; 24,8;
2–я линия: 24,3; 25,0; 25,1; 24,1; 24,6.
Обеспечивают ли обе линии одинаковую точность расфасовки?
Решение. Под точностью расфасовки понимается дисперсия измерений веса пакетов.
Необходимо проверить, равны ли дисперсии выборок с 1–й и 2–й линий.
За основную гипотезу примем гипотезу 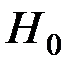 : дисперсии равны, а за конкурирующую –
: дисперсии равны, а за конкурирующую – 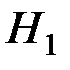 : дисперсии не равны.
: дисперсии не равны.
Зададим уровень значимости 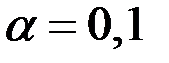 .
.
Для проверки гипотезы воспользуемся соответствующим 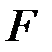 – критерием.
– критерием.
Сначала вычислим оценки величин:
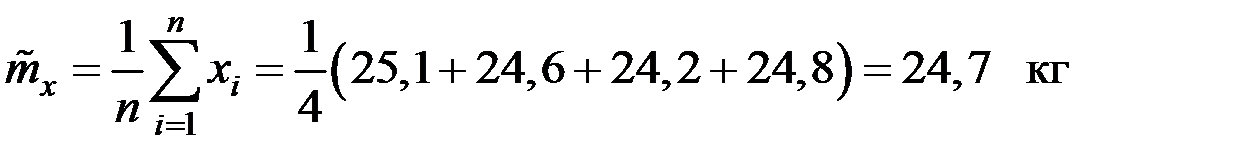 ;
;
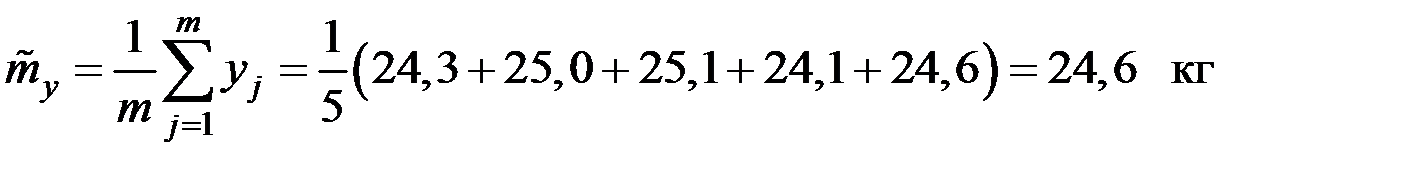 ;
;
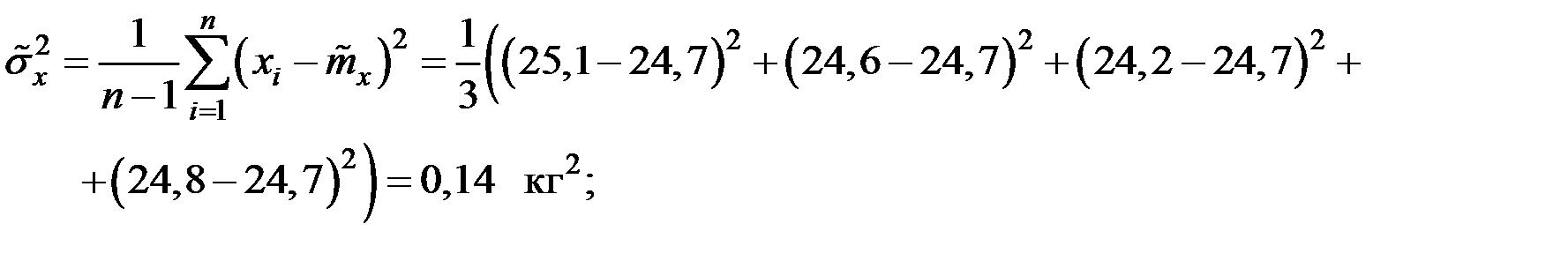
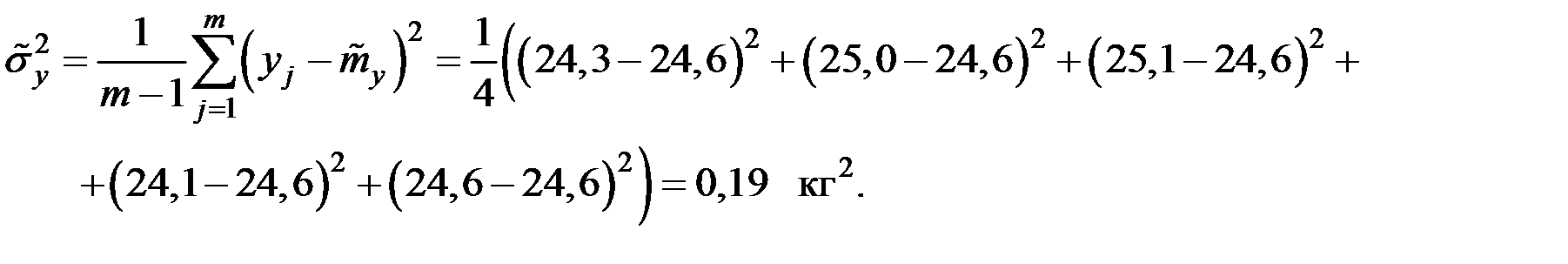
Наблюдаемое значение критерия:
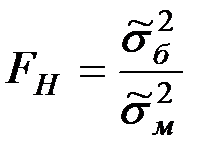 , где
, где 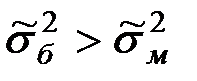 .
.
Тогда
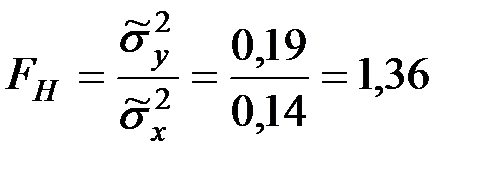 .
.
Критическое значение 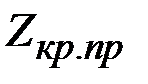 найдём по таблице квантилей
найдём по таблице квантилей 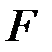 – распределения по заданному уровню значимости
– распределения по заданному уровню значимости 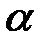 и числу степеней свободы
и числу степеней свободы 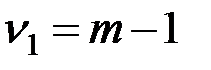 и
и 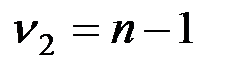 , где
, где 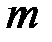 – объём выборки с большей дисперсией,
– объём выборки с большей дисперсией, 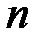 – объём выборки с меньшей дисперсией.
– объём выборки с меньшей дисперсией.
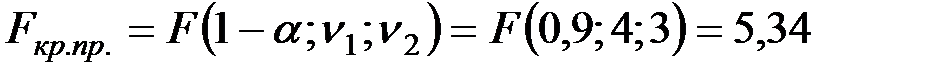 .
.
Так как 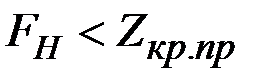 , то нет оснований отвергать гипотезу
, то нет оснований отвергать гипотезу 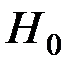 .
.
При значимости 10% исходные данные не противоречат гипотезе о том, что точность расфасовки, измеряемая дисперсией на обеих линиях одинакова.
Пример 2.2. По стандарту длина металлического стержня должна равняться 127 мм. Результаты исследований выборки из 62 стержней показали, что длина металлического стержня является нормальной случайной величиной с характеристиками (в мм): 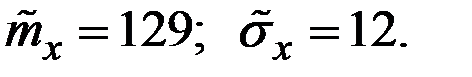
Соответствует ли выборочный результат стандарту?
Решение. Зададим уровень значимости 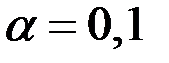 . Для проверки гипотезы воспользуемся соответствующим Т–критерием.
. Для проверки гипотезы воспользуемся соответствующим Т–критерием.
Сравним выборочную среднюю с гипотетической генеральной средней нормальной совокупности, если дисперсия генеральной совокупности неизвестна.
Имеем нулевую гипотезу:
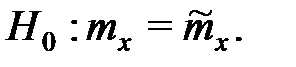
Конкурирующая гипотеза имеет вид: 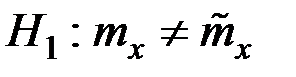 .
.
Критическая область двухсторонняя.
Наблюдаемое значение критерия
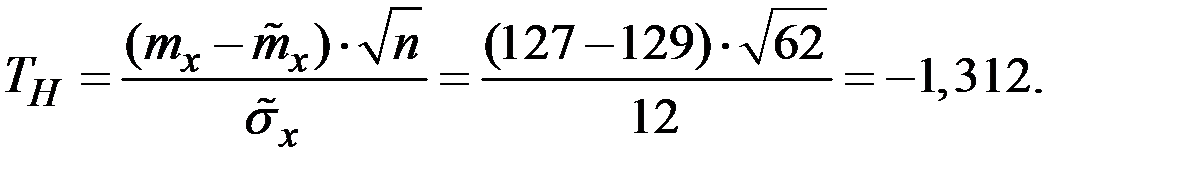
Критическое значение критерия при уровне значимости 0,1:
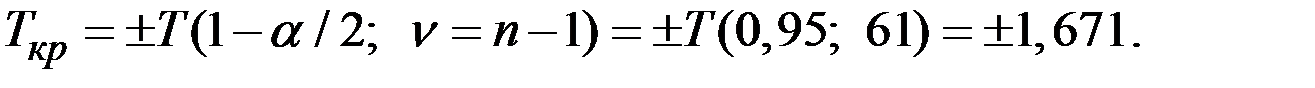
Так как по модулю 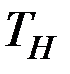 <
< 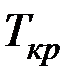 , то нет оснований отвергать нулевую гипотезу, т.е. выборочный результат соответствует стандарту.
, то нет оснований отвергать нулевую гипотезу, т.е. выборочный результат соответствует стандарту.
Пример 2.3. Партия изделий принимается, если вероятность того, что изделие окажется бракованным, не превышает 0,02. Среди случайно отобранных 480 изделий 12 оказались бракованными. Можно ли принять партию деталей?
Решение. За основную примем гипотезу 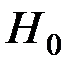 : выборочная вероятность брака равна генеральной вероятности 0,02.
: выборочная вероятность брака равна генеральной вероятности 0,02.
Конкурирующая гипотеза 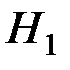 : выборочная вероятность брака больше генеральной вероятности 0,02.
: выборочная вероятность брака больше генеральной вероятности 0,02.
Зададим уровень значимости 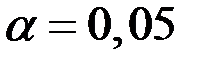 .
.
Для проверки гипотезы воспользуемся соответствующим критерием
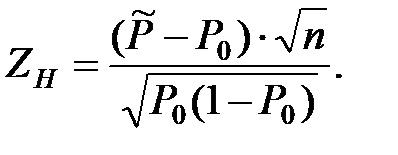
Здесь
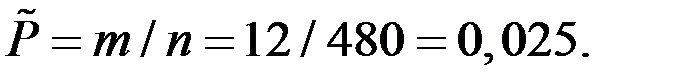
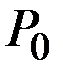 = 0,02.
= 0,02.
Тогда
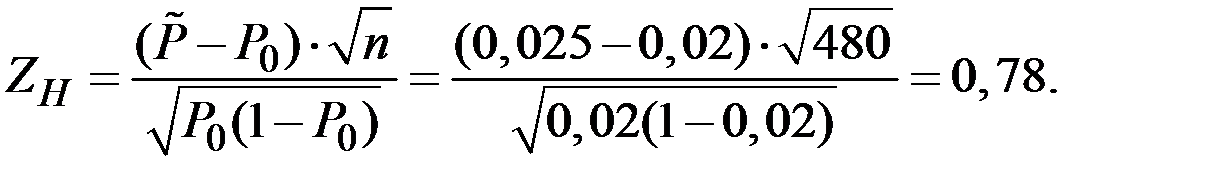
Критическое значение 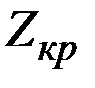 найдём по таблице функции Лапласа:
найдём по таблице функции Лапласа: 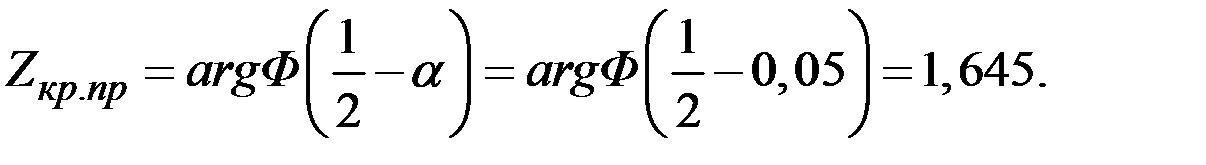
При уровне значимости 5% исходные данные не противоречат гипотезе о том, что выборочная вероятность брака равна генеральной вероятности 0,02.
Можно принять эту партию деталей.
Поставим вопрос: сколько бракованных деталей надо было иметь в выборке из 480 деталей, чтобы не принять эту партию деталей?
Вычислим 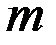 при условии, что
при условии, что 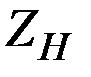 = 1,645.
= 1,645.
Вначале вычислим 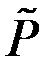 (при условии, что
(при условии, что 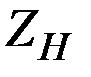 = 1,645) из уравнения:
= 1,645) из уравнения:
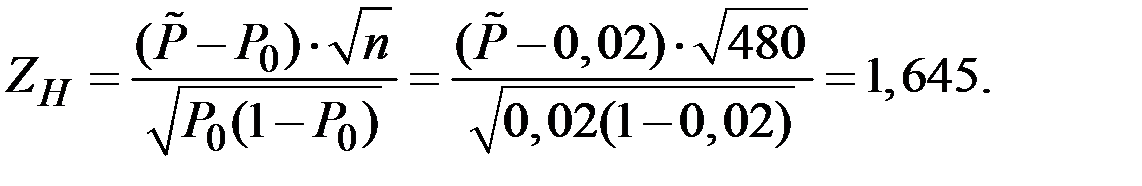
Получаем: 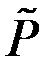 = 0,0305.
= 0,0305.
Тогда
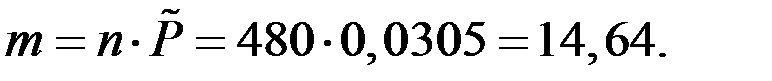
Чтобы не принять рассматриваемую партию деталей необходимо было иметь 15 бракованных деталей из 480.
Пример 2.4. По выборке объёма n, извлечённой из нормальной генеральной совокупности с известной дисперсией s 2, найдена выборочная средняя 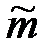 . При уровне значимости a требуется найти функцию мощности критерия проверки гипотезы H0: a = a0 о равенстве генеральной средней a гипотетическому значению a0 при конкурирующей гипотезе H1: a = a1 № a0.
. При уровне значимости a требуется найти функцию мощности критерия проверки гипотезы H0: a = a0 о равенстве генеральной средней a гипотетическому значению a0 при конкурирующей гипотезе H1: a = a1 № a0.
Решение. Сравнение выборочной средней с гипотетической средней для указанных условий производится по критерию
ZН 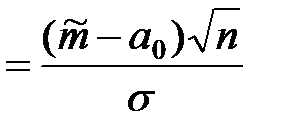 , при этом
, при этом 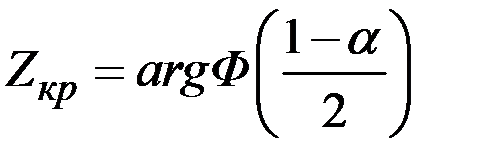 .
.
Двусторонняя критическая область определяется неравенством
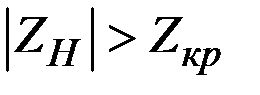 .
.
Мощность 1 – b рассматриваемого критерия, то есть вероятность попадания критерия в критическую область при допущении, что справедлива конкурирующая гипотеза H1 : a = a1 № a0, определяется соотношением :
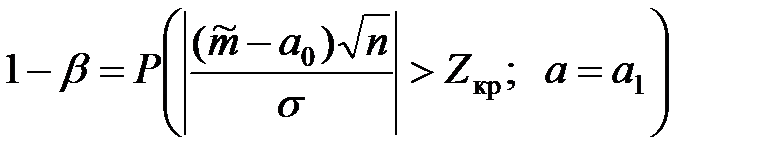 .
.
Преобразуем выражение, стоящее под знаком модуля :
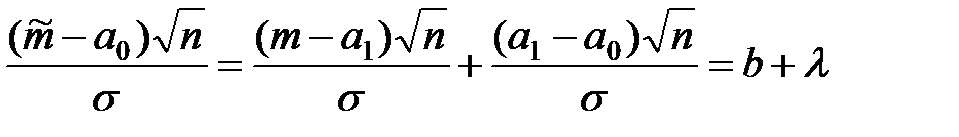 ,
,
где
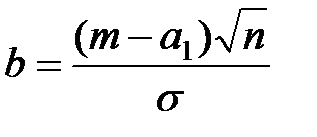 ;
; 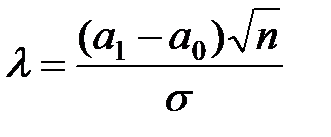 .
.
В этих обозначениях имеем :
1 – b = P(|b + l| > Zкр) = P(b + l > Zкр) + P(b + l < – Zкр) =
= P(b > Zкр – l) + P(b < – Zкр – l) = 1 – P(b < Zкр – l) + P(b < – Zкр – l) =
= 1 – F( Zкр – l) + F(– Zкр – l ) = 1 – F(Zкр – l) – F(Zкр + l).
Искомая мощность двустороннего критерия есть функция от a1:
1 – b = j(a1) = 1 – [F(Zкр – l) + F( Zкр + l)],
где F(x) – функция Лапласа;
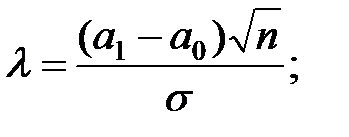
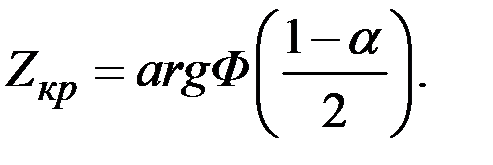
Можно убедиться, что увеличение объёма выборки и уровня значимости влекут увеличение мощности критерия.
Вычислим мощность рассматриваемого критерия для частного случая при: n = 16; s = 5; a = 0,05;
H0: a = a0 = 20; H1 : a = a1 =24.
Имеем 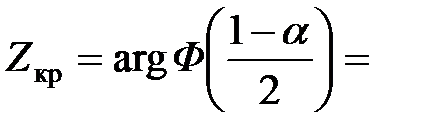 1,96;
1,96; 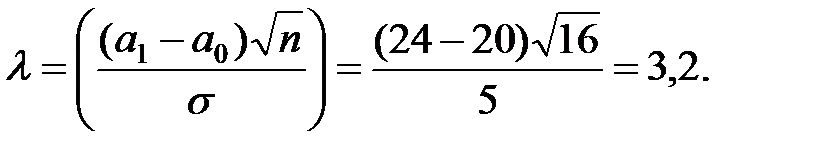
Тогда 1 – b = 1 – [F(1,96 – 3,2) + F(1,96 + 3,2)] = 1 + F(1,24) – F(5,16) =
= 1 + 0,392 – 0,5 = 0,892.
Несложно получить функцию мощности аналогичного критерия при конкурирующей гипотезе H1 : a = a1 > a0.
В этом случае имеем правостороннюю критическую область и тогда
1 – b = 0,5 – F(Zкр – l), где Zкр = arg F(0,5 – a); 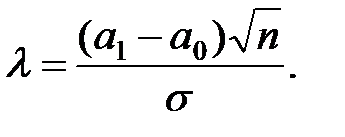
Определим, например, необходимый объём выборки n, при котором мощность одностороннего критерия будет не менее 0,6 , если s = 4; a = 0,05 и проверяется гипотеза H0 : a = a0 = 2 при конкурирующей гипотезе H1: a = a1 = 3 > 2.
Для этого из соотношения 0,6 і 0,5 – F(Zкр – l) найдём вначале параметр l, обеспечивающий это неравенство, а из него величину n.
Имеем:
Zкр = arg F(0,5 – 0,05) = 1,65;
F(l – 1,65) Ј 0,1; l – 1,65 Ј 0,253;
l Ј 1,903; 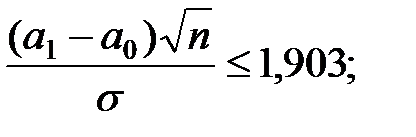
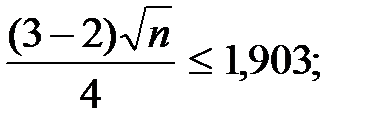
n і 58.
Пример 2.5. Допустимый процент (норматив) штампованных деталей, требующих доработки, составляет 5%. Из 500 взятых для контроля деталей доработка потребовалась для 30 из них. Согласуются ли данные выборочного контроля с нормативом?
Решение. Требуется проверить гипотезу о том, превышает ли сколько–нибудь существенно процент дорабатываемых деталей в 5% или нет.
Для проверки гипотезы
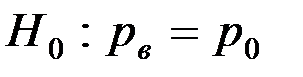
о равенстве выборочной и генеральной вероятностей соответствующего события используем критерий
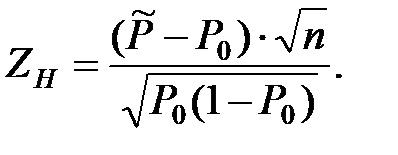 ,
,
где 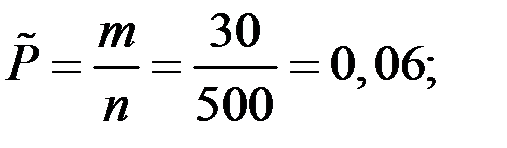
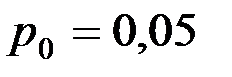 .
.
Вычислим наблюдаемое значение критерия
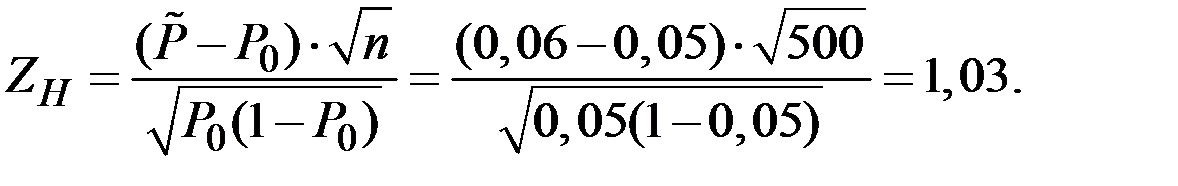
При 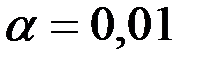 с помощью табличной функции Лапласа найдём критическую точку.
с помощью табличной функции Лапласа найдём критическую точку.
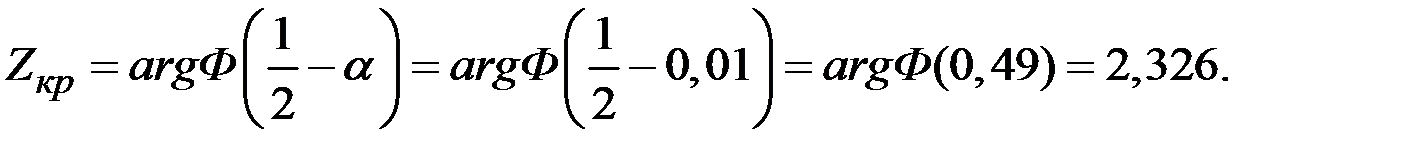
При 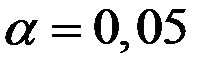
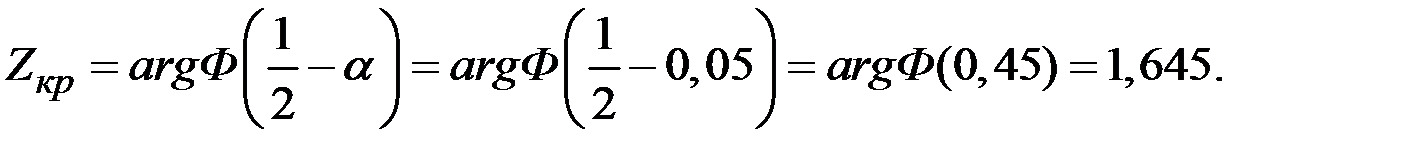
При 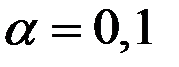
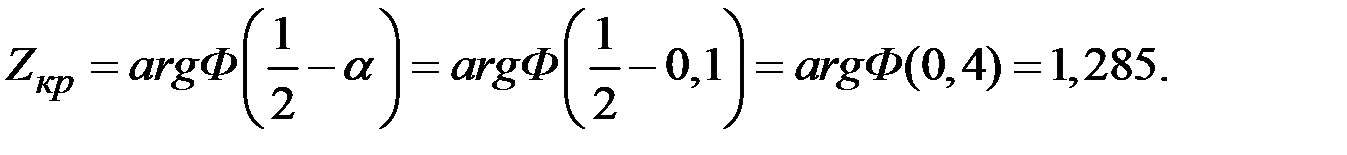
Так как 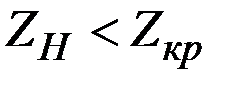 , то результат контроля не противоречит выдвинутой гипотезе, а значит, процент брака в выборке случайно расходится с допустимой величиной 5%.
, то результат контроля не противоречит выдвинутой гипотезе, а значит, процент брака в выборке случайно расходится с допустимой величиной 5%.
Критерий Пирсона
Критерий Пирсона (критерий 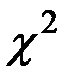 ) широко применяют для проверки гипотез о предполагаемом законе распределения.
) широко применяют для проверки гипотез о предполагаемом законе распределения.
Если эмпирическое распределение задано в виде последовательности равноотстоящих вариант 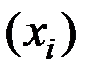 или в виде соседних интервалов
или в виде соседних интервалов 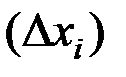 и соответствующих им частот
и соответствующих им частот 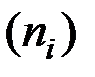 , то наблюдаемое значение критерия Пирсона в этом случае вычисляется по формуле
, то наблюдаемое значение критерия Пирсона в этом случае вычисляется по формуле
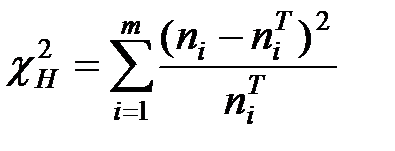 ,
,
где 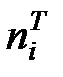 – теоретические частоты для проверяемого закона распределения.
– теоретические частоты для проверяемого закона распределения.
Критическое значение 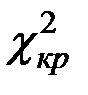 находится по таблице квантилей
находится по таблице квантилей 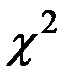 –распределения по заданному уровню значимости
–распределения по заданному уровню значимости 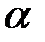 и числу степеней свободы
и числу степеней свободы 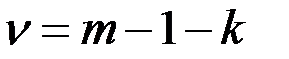 , где k – количество параметров закона распределения, оцениваемых по выборке.
, где k – количество параметров закона распределения, оцениваемых по выборке.
2.3.1. Теоретические частоты 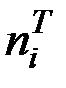 для нормального закона распределения можно получить с использованием функции Лапласа:
для нормального закона распределения можно получить с использованием функции Лапласа:
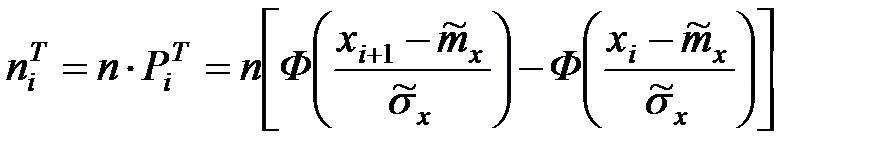 ,
,
где 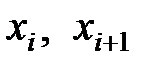 – границы i–го интервала в эмпирическом распределении (в гистограмме);
– границы i–го интервала в эмпирическом распределении (в гистограмме);
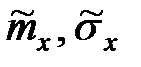 – выборочные оценки математического ожидания и среднего квадратического отклонения СВ Х;
– выборочные оценки математического ожидания и среднего квадратического отклонения СВ Х;
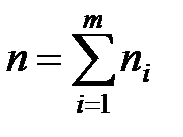 – объём выборки.
– объём выборки.
При этом 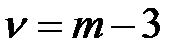 .
.
2.3.2. Для показательного закона теоретические частоты
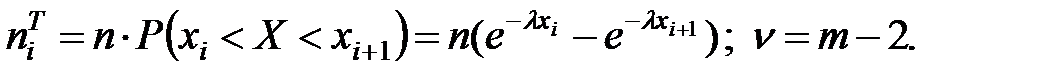
2.3.3. Для биномиального распределения
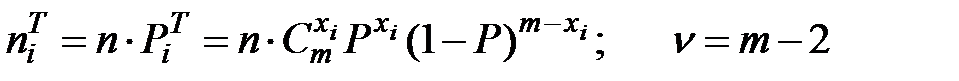 ,
,
где P – вероятность появления события в каждом испытании;
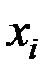 – число появлений события в одном опыте, состоящем из m независимых испытаний
– число появлений события в одном опыте, состоящем из m независимых испытаний 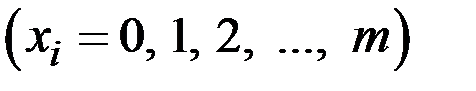 .
.
2.3.4. Для закона Пуассона теоретические частоты
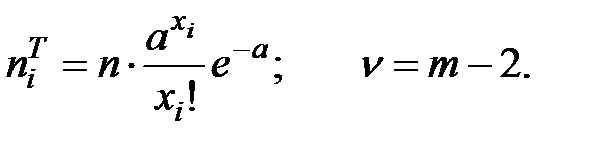
2.3.5. Критерий Пирсона позволяет также проверить гипотезу о независимости двух СВ X и Y по выборке 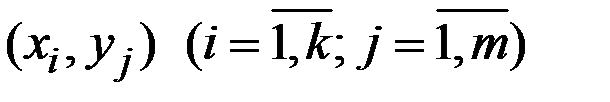 .
.
В этом случае
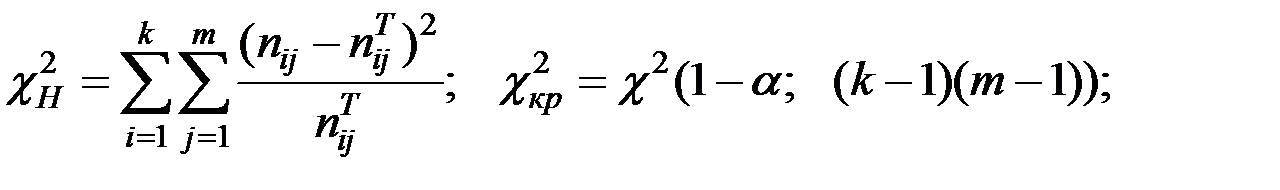
где 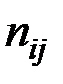 – число случаев, когда одновременно наблюдались значения
– число случаев, когда одновременно наблюдались значения 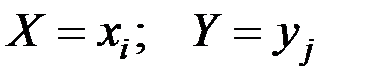 (для непрерывных X и Y i и j – номера соответствующих разрядов);
(для непрерывных X и Y i и j – номера соответствующих разрядов);
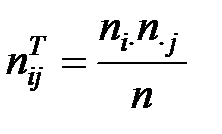 ;
; 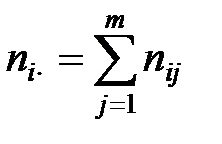 ;
; 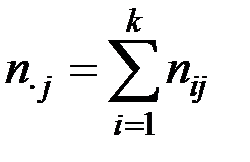 ;
; 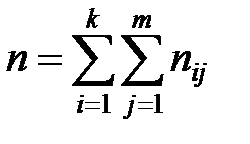 ;
;
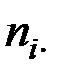 – общее число случаев, когда наблюдалось значение
– общее число случаев, когда наблюдалось значение 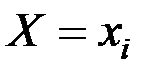 ;
;
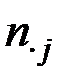 – общее число случаев, когда наблюдалось значение
– общее число случаев, когда наблюдалось значение 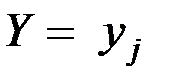 ;
;
n – объём выборки.
2.3.6. Критерий 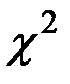 используют и для проверки однородности данных любого числа выборок, имеющих дискретную структуру или сводимых к этому соответствующей группировкой.
используют и для проверки однородности данных любого числа выборок, имеющих дискретную структуру или сводимых к этому соответствующей группировкой.
Пусть осуществлено k серий независимых наблюдений, объёмы которых 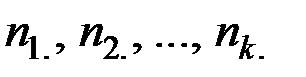 , и в каждой серии наблюдался некоторый признак, принимающий одно из m возможных значений (исходов).
, и в каждой серии наблюдался некоторый признак, принимающий одно из m возможных значений (исходов).
Пусть 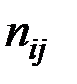 – число реализаций j–го исхода в i–й серии
– число реализаций j–го исхода в i–й серии
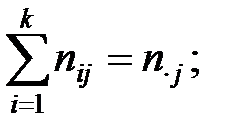
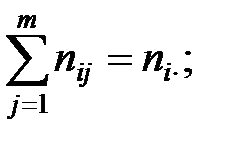
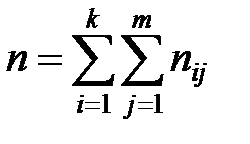 .
.
Требуется проверить гипотезу 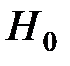 о том, что все наблюдения производились над одной и той же СВ.
о том, что все наблюдения производились над одной и той же СВ.
Статистикой 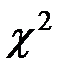 – критерия в данном случае является величина
– критерия в данном случае является величина
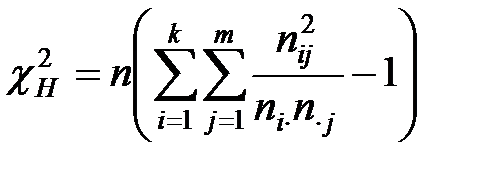 ;
;
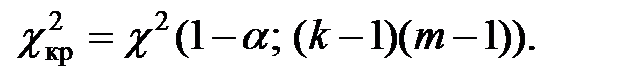
Пример 2.6. Проверили 165 ящиков. Оказалось, что в 94 ящиках все изделия были стандартными, в 46 ящиках было одно бракованное, в 20 – 2 бракованных, в 2 – 3 бракованных, в 3 – 4 бракованных изделия. Подчиняется ли число бракованных изделий в ящиках закону Пуассона?
Решение. Имеем следующую статистику:
Кол. брака 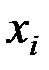
| 0 | 1 | 2 | 3 | 4 |
Частота, 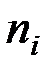
| 94 | 46 | 20 | 2 | 3 |
Выборочная средняя бракованных изделий в ящиках равна
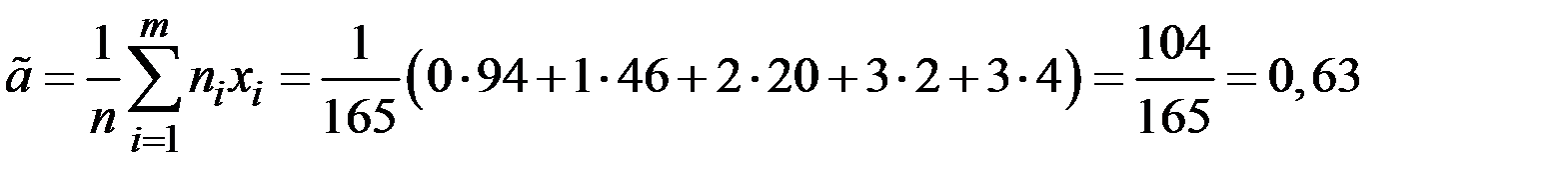 .
.
Предполагаемый закон Пуассона имеет вид
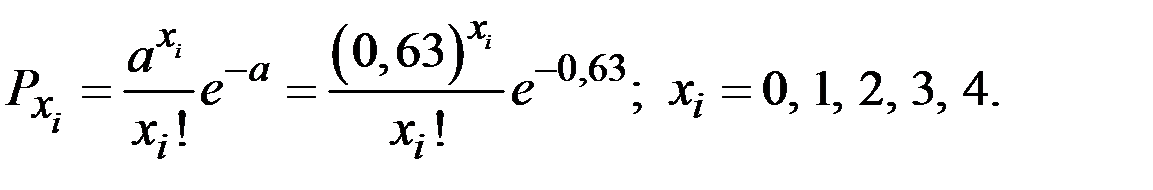
Вычислим теоретические частоты для проверяемого закона распределения:
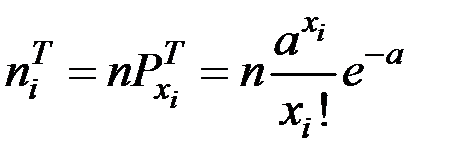 ;
;
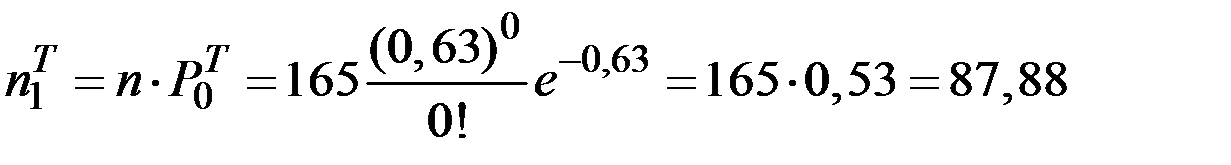 ;
;
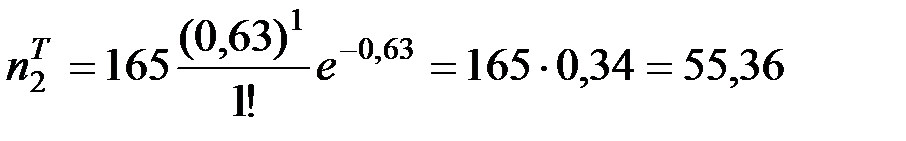 ;
;
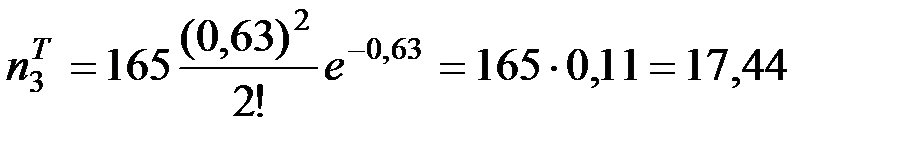 ;
;
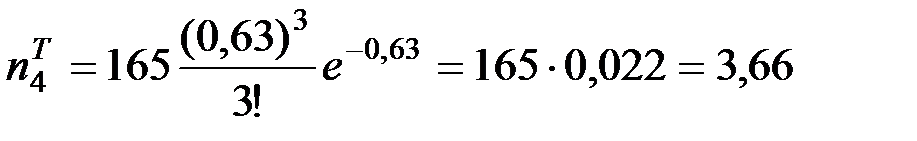 ;
;
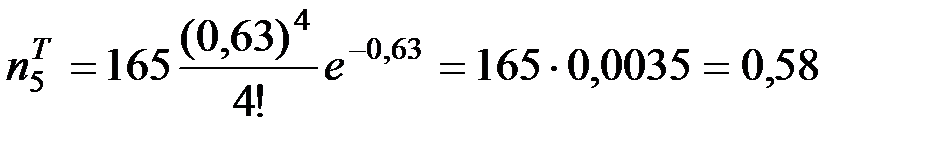 .
.
Вычислим наблюдаемое значение критерия:
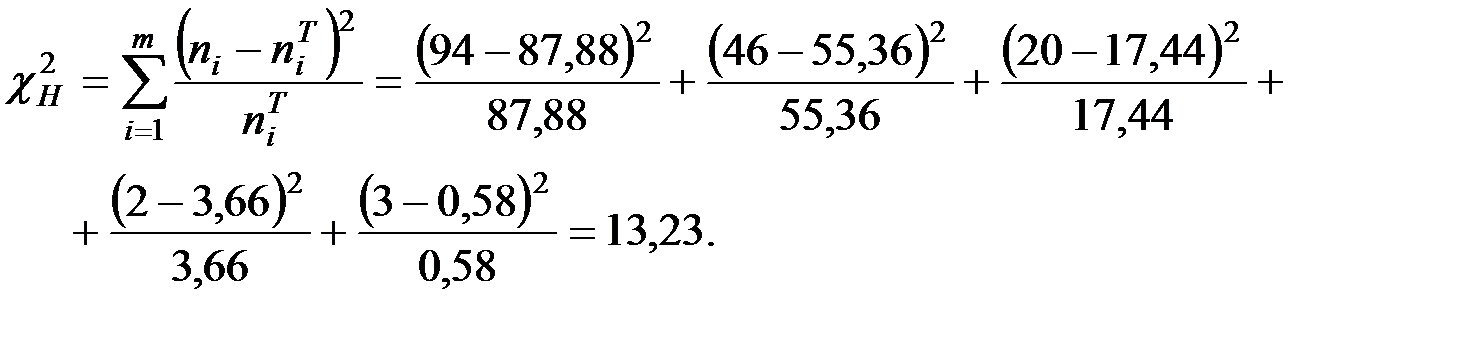
Критическое значение 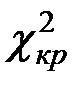 найдём по таблице квантилей
найдём по таблице квантилей 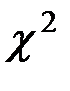 – распределения по заданному уровню значимости
– распределения по заданному уровню значимости 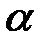 и числу степеней свободы
и числу степеней свободы 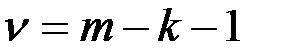 , где
, где 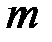 – количество интервалов,
– количество интервалов, 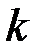 – количество вычисленных параметров закона распределения.
– количество вычисленных параметров закона распределения.
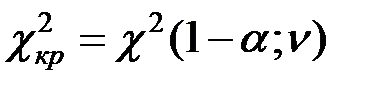 , где
, где 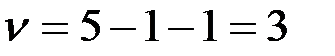 ;
;
При 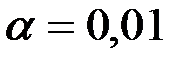
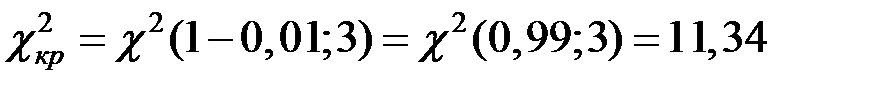 .
.
При 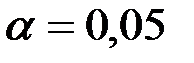
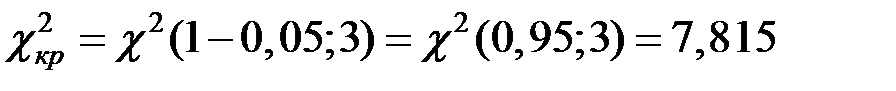 .
.
При 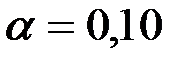
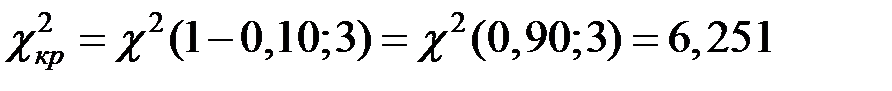 .
.
Так как  , то отвергаем гипотезу о том, что распределение бракованных изделий подчиняется закону Пуассона.
, то отвергаем гипотезу о том, что распределение бракованных изделий подчиняется закону Пуассона.
Пример 2.7. Проведены наблюдения за временем пребывания клиента в автосервисе. Данные по 165 клиентам приведены ниже:
Продолжительность 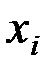 пребывания клиента в фирме, час. пребывания клиента в фирме, час.
| 0 – 1 | 1 – 2 | 2 – 3 | 3 – 4 | 4 и более |
Количество клиентов, 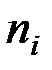
| 94 | 46 | 20 | 2 | 3 |
Подчиняется ли время пребывания клиентов в автосервисе показательному закону?
Решение. Используем критерий Пирсона. Имеем 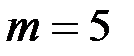 .
.
Определим среднее пребывание клиента в автосервисе, взяв середину интервала в качестве 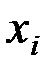
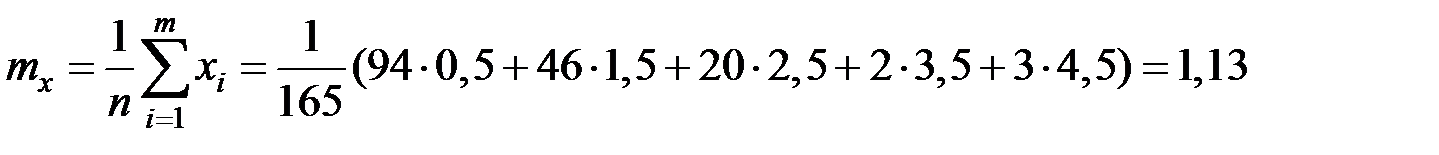 .
.
Тогда 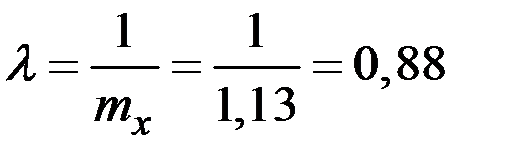 .
.
Показательный закон имеет вид 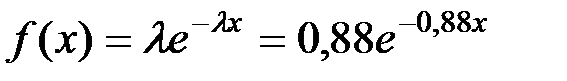 .
.
Вычислим теоретические частоты для проверяемого закона распределения: 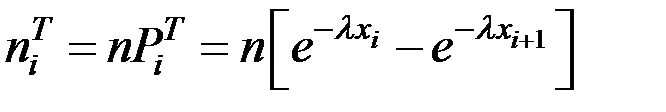 ;
;
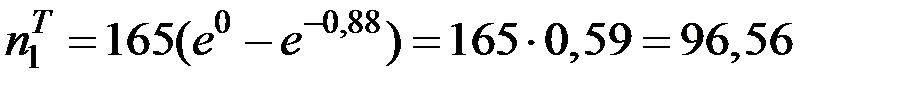 ;
;
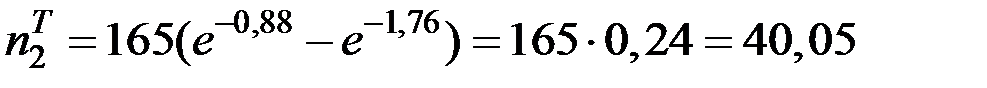 ;
;
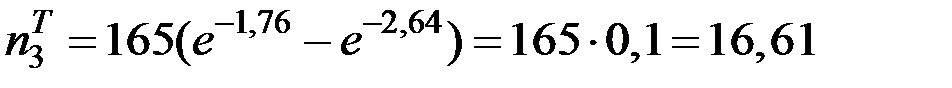 ;
;
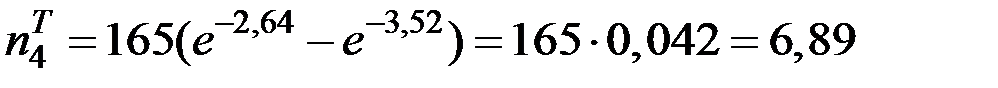 ;
;
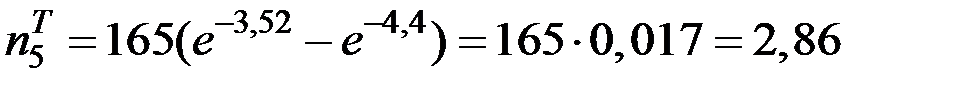 .
.
Вычислим наблюдаемое значение критерия:
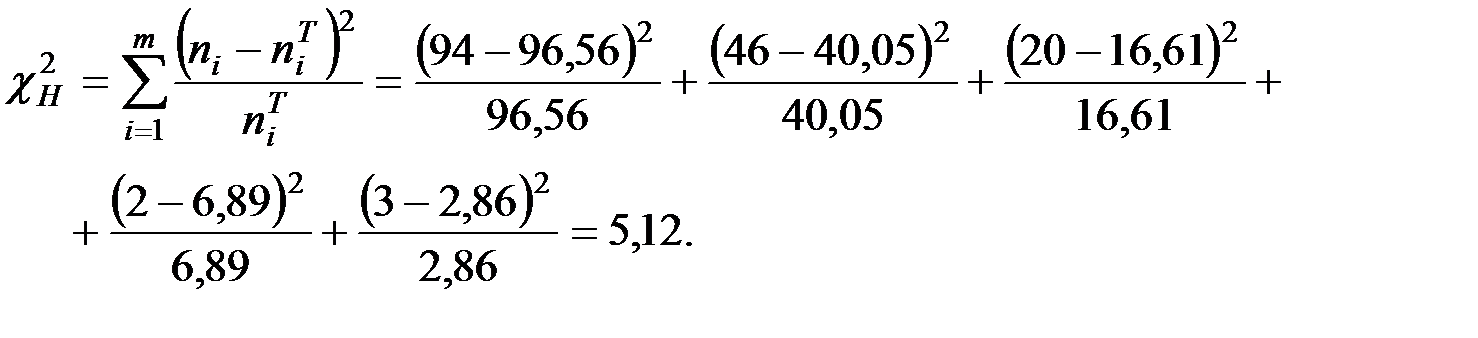
Критическое значение 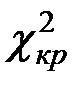 найдём по таблице квантилей
найдём по таблице квантилей 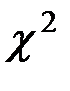 – распределения по заданному уровню значимости
– распределения по заданному уровню значимости 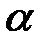 и числу степеней свободы
и числу степеней свободы 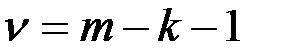 , где
, где 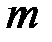 – количество интервалов,
– количество интервалов, 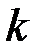 – количество вычисленных параметров закона распределения.
– количество вычисленных параметров закона распределения.
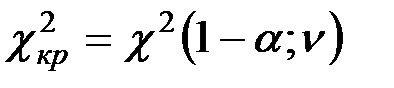 , где
, где 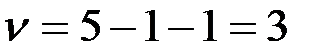 ;
;
При 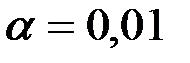
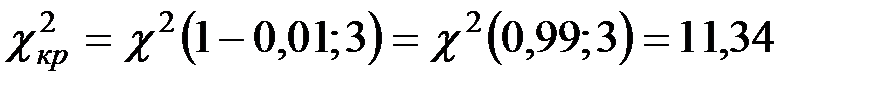 ;
;
При 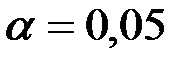
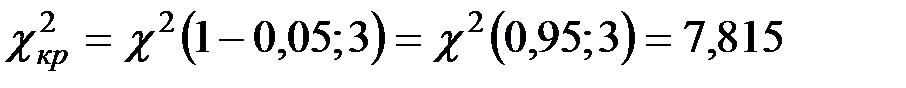 ;
;
При 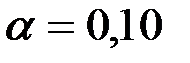
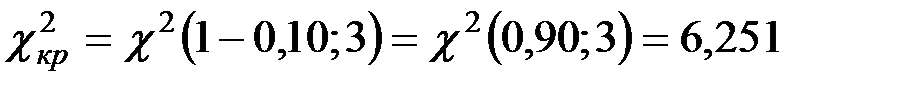 .
.
Так как 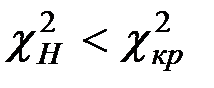 , то нет оснований отвергать гипотезу о показательном распределении времени пребывания клиентов в автосервисе.
, то нет оснований отвергать гипотезу о показательном распределении времени пребывания клиентов в автосервисе.
Пример 2.8. Пятьдесят опрошенных рабочих дали следующую информацию об их недельной зарплате:
Зарплата 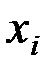 , тыс. р. , тыс. р.
| 2,5 – 4,5 | 4,5 – 6,5 | 6,5 – 8,5 | 8,5 – 10,5 | 10,5 – 12,5 |
Количество человек, 
| 5 | 8 | 19 | 15 | 3 |
Подчиняется ли зарплата на предприятии нормальному закону?
Решение. Определим среднюю зарплату предприятия, взяв середину интервала в качестве 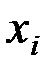
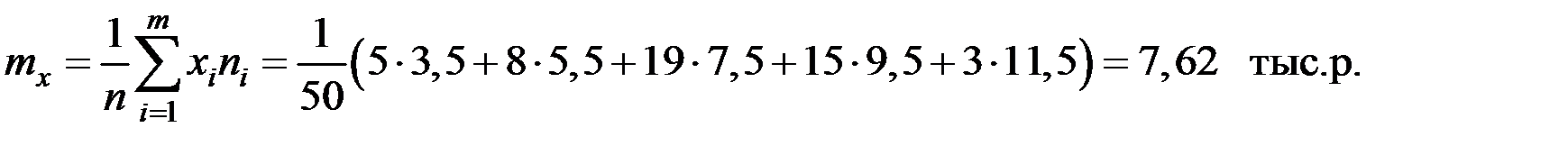
Вычислим дисперсию:
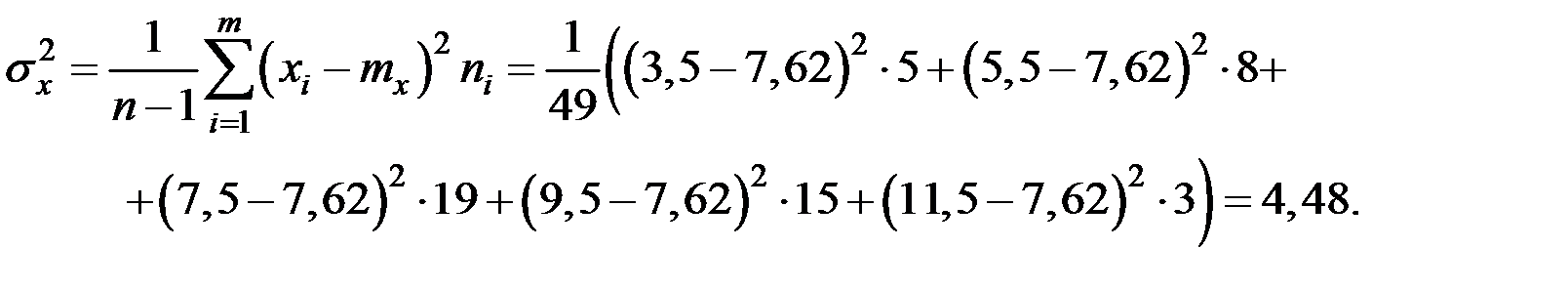
Тогда среднее квадратическое отклонение равно:
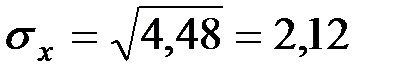 .
.
Получим закон распределения зарплаты на предприятии
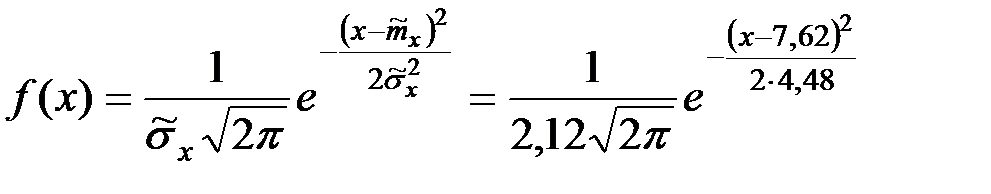 .
.
За основную гипотезу примем гипотезу 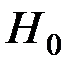 : зарплата на предприятии подчиняется нормальному закону, а за конкурирующую –
: зарплата на предприятии подчиняется нормальному закону, а за конкурирующую – 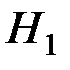 : зарплата на предприятии не подчиняется нормальному закону.
: зарплата на предприятии не подчиняется нормальному закону.
Зададим уровень значимости 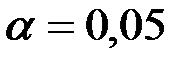 .
.
Для проверки гипотезы воспользуемся критерием Пирсона.
Имеем 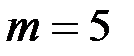 . Вычислим теоретические частоты для проверяемого закона распределения:
. Вычислим теоретические частоты для проверяемого закона распределения:
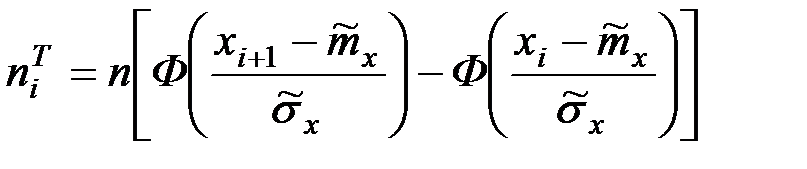 ;
;
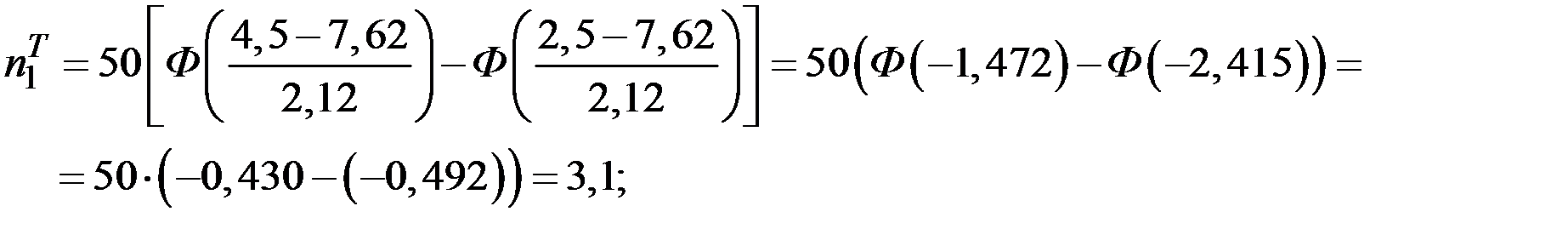
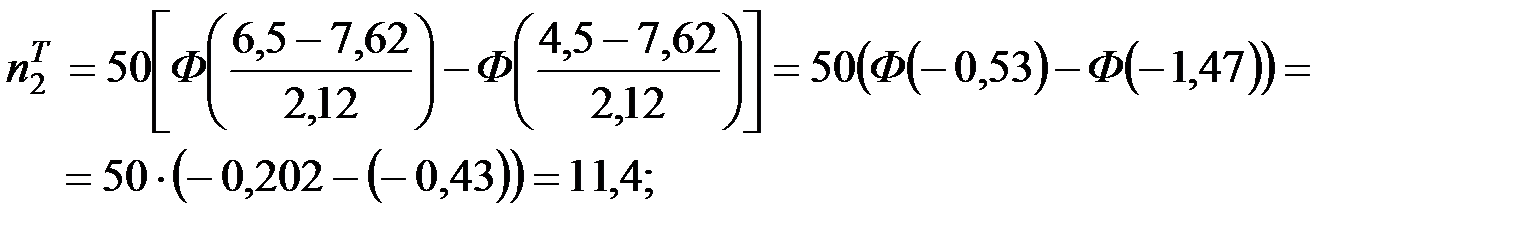
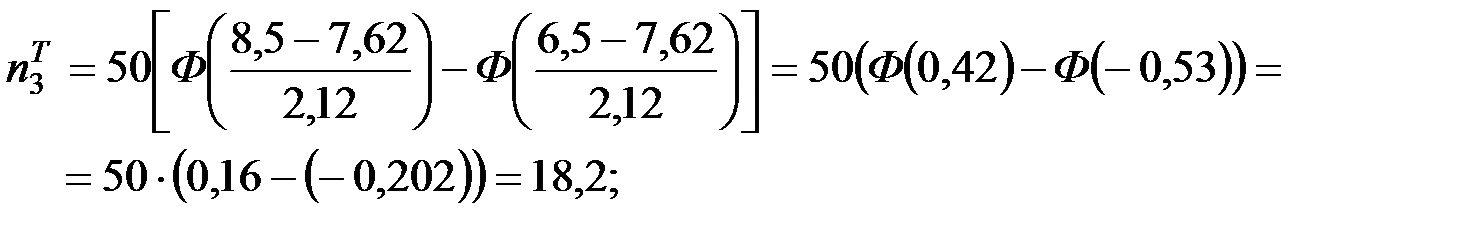
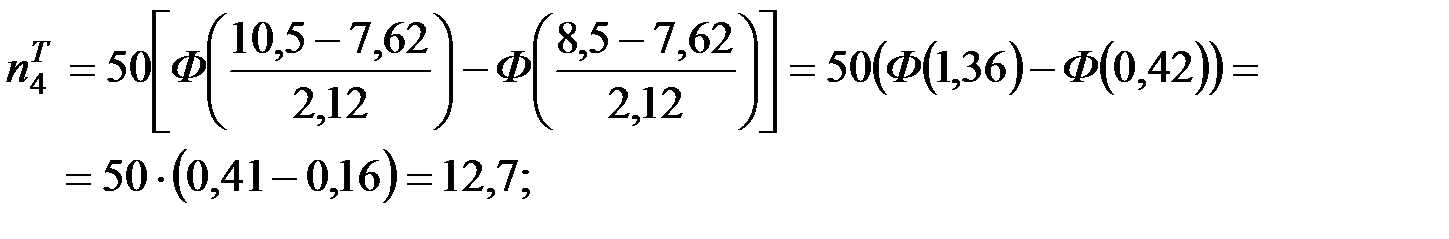
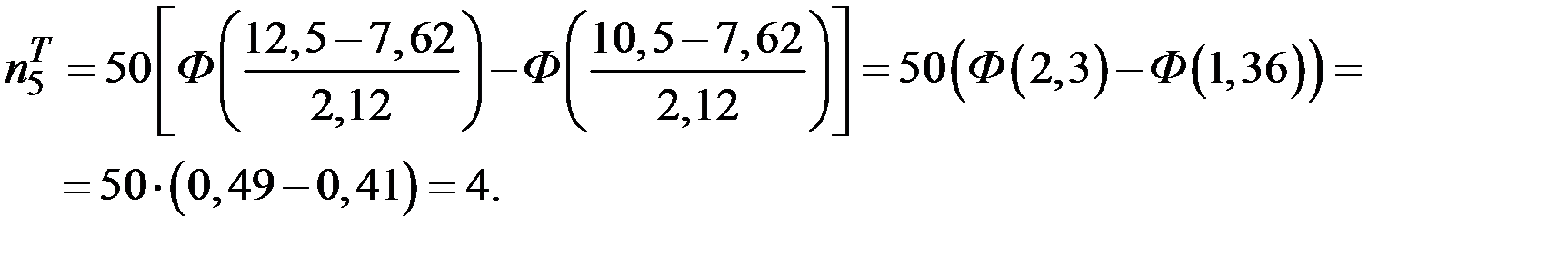
Вычислим наблюдаемое значение критерия:
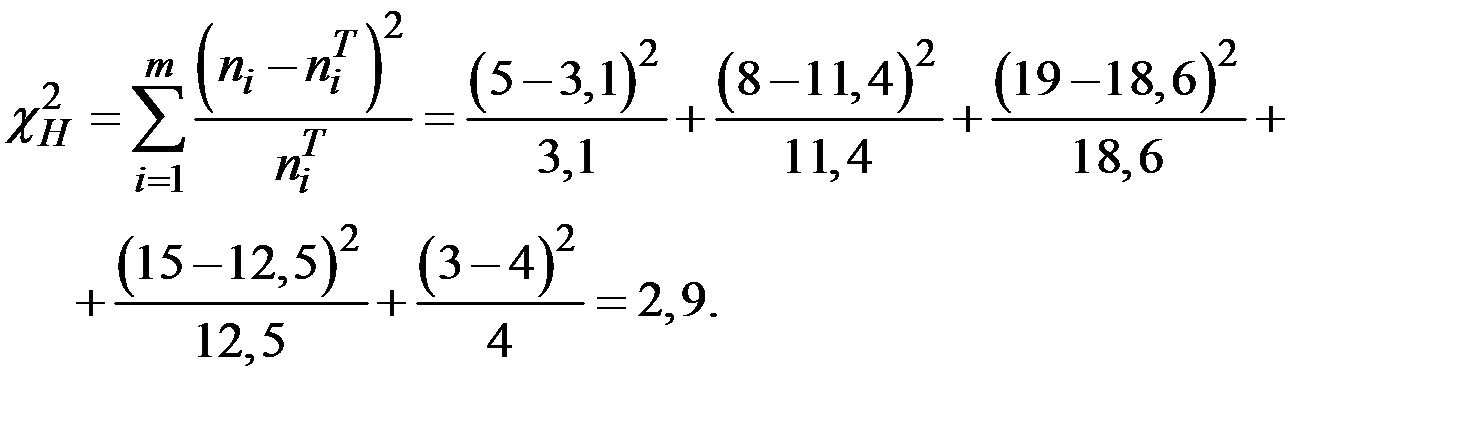
Критическое значение 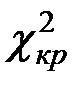 найдём по таблице квантилей
найдём по таблице квантилей 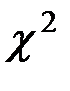 – распределения по заданному уровню значимости
– распределения по заданному уровню значимости 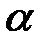 и числу степеней свободы
и числу степеней свободы
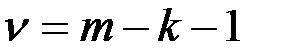 ,
,
где 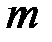 – количество интервалов,
– количество интервалов,
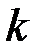 – количество вычисленных параметров закона распределения.
– количество вычисленных параметров закона распределения.
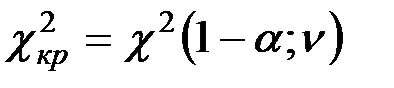 , где
, где 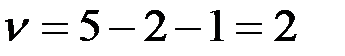 .
.
При 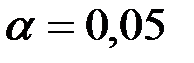
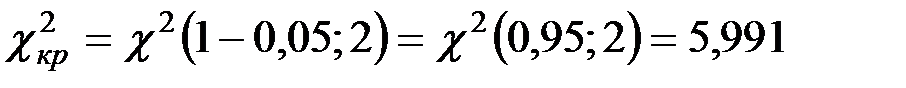 .
.
Так как 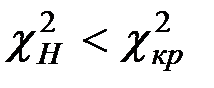 , то нет оснований отвергать гипотезу
, то нет оснований отвергать гипотезу 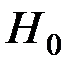 о том, что зарплата на предприятии имеет нормальный закон распределения.
о том, что зарплата на предприятии имеет нормальный закон распределения.
Но это не является доказательством того, что зарплата подчиняется только нормальному закону. Эту переменную можно описать и многими другими законами.
Пример 2.9. Статистика показывает, что в университете по математике 20% студентов получают неудовлетворительные оценки, 25% студентов – тройки, 33% студентов – четвёрки, 22% студентов – отлично. Из 500 студентов некоторого факультета двойки получили 80 человек, тройки – 130 человек, четвёрки – 180 человек, пятёрки – 110 человек. Согласуется ли статистика факультета с общеуниверситетской статистикой?
Решение. Проверим гипотезу 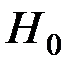 : вероятность получения оценки (2, 3, 4 или 5) на факультете совпадает с вероятностью получения соответствующей оценки (2, 3, 4 или 5) в университете в целом, то есть
: вероятность получения оценки (2, 3, 4 или 5) на факультете совпадает с вероятностью получения соответствующей оценки (2, 3, 4 или 5) в университете в целом, то есть
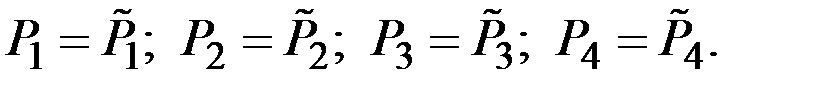
Используем критерий Пирсона: 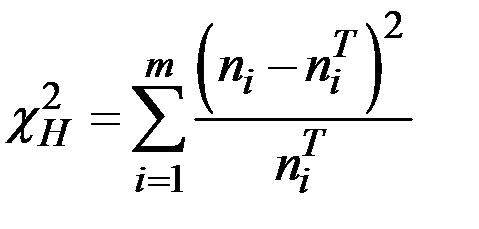 .
.
Здесь 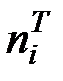 – теоретическая частота (сколько раз) появления признака в i–ом интервале (
– теоретическая частота (сколько раз) появления признака в i–ом интервале ( 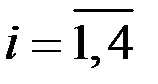 ):
): 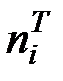 =
= 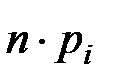 ;
;
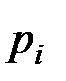 – вероятность попадания величины, распределённой по нормальному закону в i–ый интервал (площадь i–го интервала).
– вероятность попадания величины, распределённой по нормальному закону в i–ый интервал (площадь i–го интервала).
Тогда 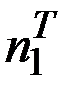 =
= 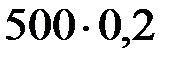 =
= 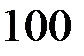 ;
; 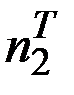 =
= 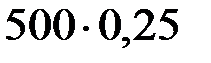 =
= 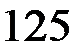 ;
;
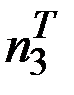 =
= 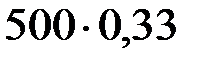 =
= 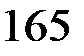 ;
; 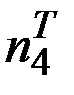 =
= 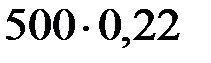 =
= 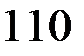 .
.
Имеет сравнительную статистику:
| Оценки | “2” | “3” | “4” | “5” |
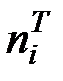
| 100 | 125 | 165 | 110 |
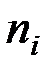
| 80 | 130 | 180 | 110 |
Вычислим наблюдаемое значение критерия ( 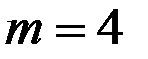 ):
):
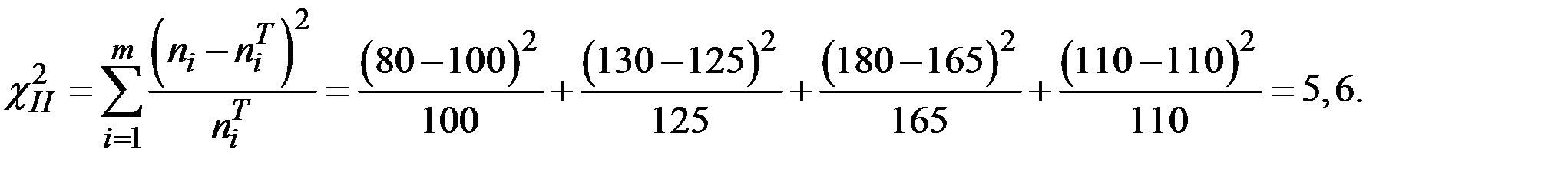
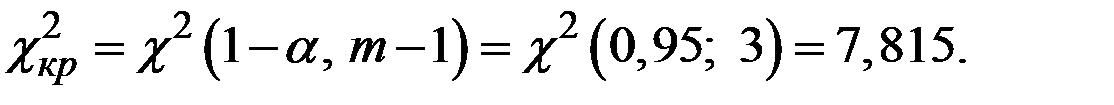
Так как 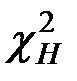 <
< 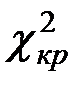 , то нет оснований отвергать гипотезу
, то нет оснований отвергать гипотезу 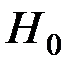 о том, что вероятность получения оценки (2, 3, 4 или 5) на факультете совпадает с вероятностью получения соответствующей оценки (2, 3, 4 или 5) в университете в целом.
о том, что вероятность получения оценки (2, 3, 4 или 5) на факультете совпадает с вероятностью получения соответствующей оценки (2, 3, 4 или 5) в университете в целом.
Пример 2.10. Поступающие в университет абитуриенты разбиты на два потока по 300 человек в каждом. Баллы 2, 3, 4, 5 на экзамене по математике получили соответственно 33, 43, 80, 144 абитуриента, а во втором потоке – 39, 35, 72, 154. Можно ли считать оба потока однородными?
Решение. Имеем k = 2, m = 4;
Первая выборка:
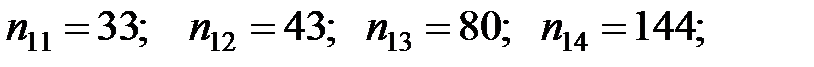
вторая выборка:
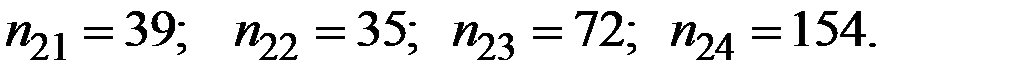
Получаем в итоге:
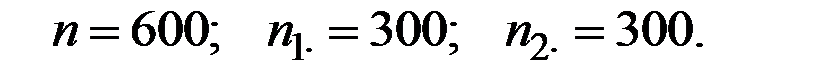
Критическое значение критерия при 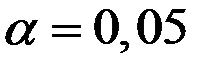 :
:
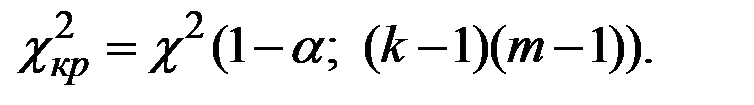
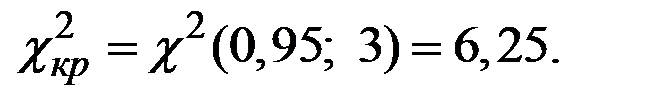
Наблюдаемое значение критерия:
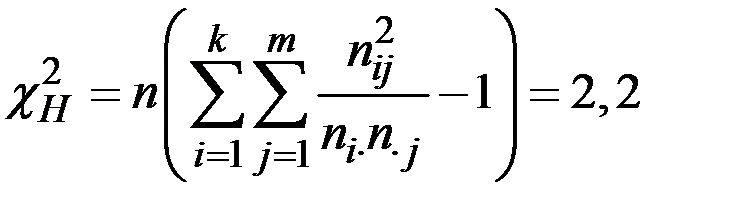 .
.
Так как 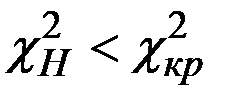 , то следует считать оба потока однородными, т.е. взятыми из одной генеральной совокупности.
, то следует считать оба потока однородными, т.е. взятыми из одной генеральной совокупности.
Пример 2.11. Дана выборка объёмом 30 значений дневной выручки магазина (СВ Х) (в тыс. руб.): 22,417; 21,010; 24,061; 23,238; 20,794; 19,037; 18,377; 22,997; 22,325; 19,141; 20,502; 24,149; 23,042; 20,288; 18,537; 19,220; 22,629; 23,872; 22,729; 18,271; 17,491; 20,544; 19,432; 23,417; 22,506; 20,246; 19,557; 7,844; 20,220; 19,077.
На основании этих данных: построить интервальный статистический ряд и гистограмму; вычислить среднее и среднее квадратическое отклонение СВ Х; получить точечные и интервальные оценки математического ожидания и дисперсии генеральной совокупности для доверительной вероятности 0,95. Проверить гипотезу о нормальности распределении данных по критерию Пирсона при уровне значимости 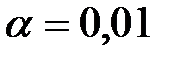 .
.
Решение. Интервальный статистический ряд имеет вид:
| Интервал | 17–18 | 18–19 | 19–20 | 20–21 | 21–22 | 22–23 | 23–24 | 24–25 |
| Середина интервала | 17,5 | 18,5 | 19,5 | 20,5 | 21,5 | 22,5 | 23,5 | 24,5 |
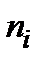 (частота) (частота)
| 2 | 3 | 6 | 6 | 1 | 6 | 4 | 2 |
Гистограмма распределения интервального статистического ряда дневной выручки магазина представлена на рис. 2.3.
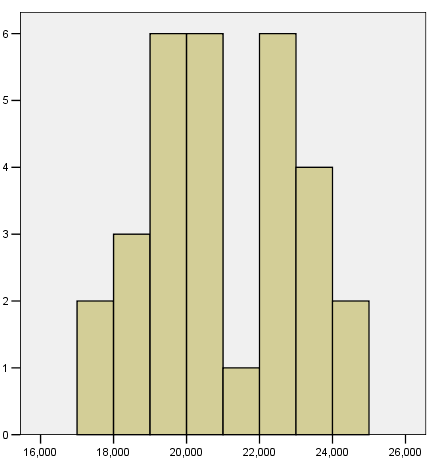
Рис. 2.3. Гистограмма распределения дневной выручки магазина
Вычислим среднее значение, дисперсию и среднее квадратическое отклонение дневной выручки магазина ( 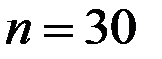 ):
):
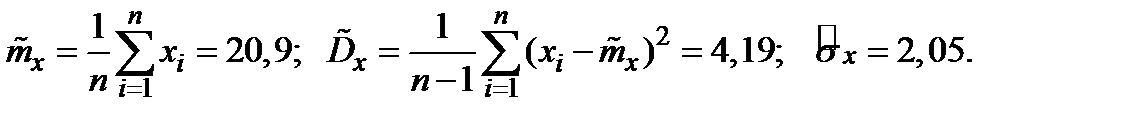
Получим интервальные оценки математического ожидания и дисперсии генеральной совокупности:
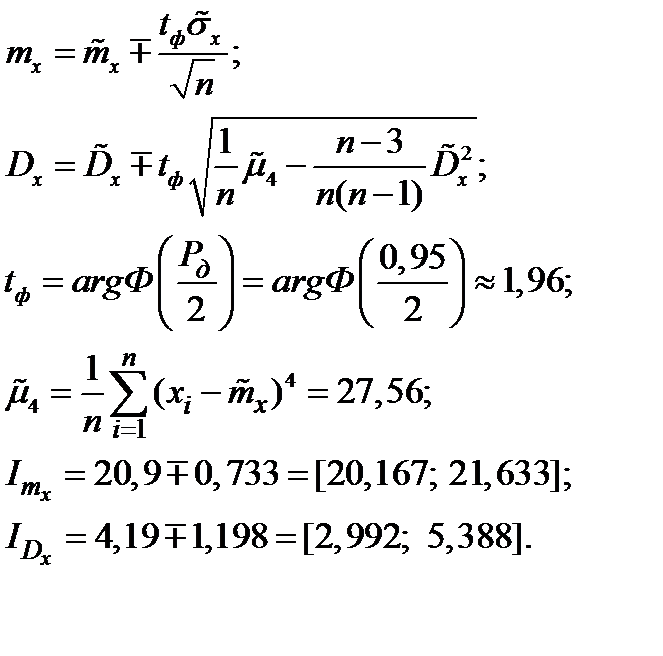
Проверим гипотезу 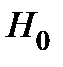 о нормальном распределении генеральной совокупности по критерию Пирсона при уровне значимости
о нормальном распределении генеральной совокупности по критерию Пирсона при уровне значимости 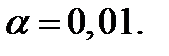
Найдём теоретические частоты по соотношению
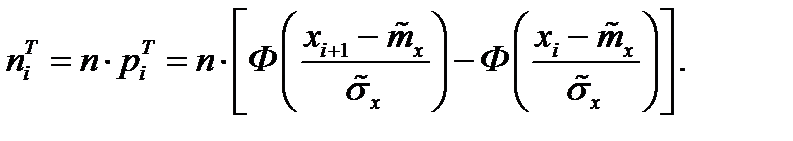
В итоге наблюдаемое значение критерия Пирсона будет равно
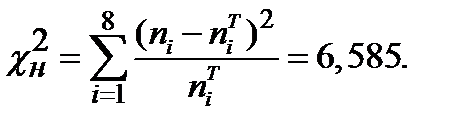
Критическое значение критерия 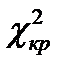 находим по таблице квантилей хи– квадрат распределения:
находим по таблице квантилей хи– квадрат распределения:
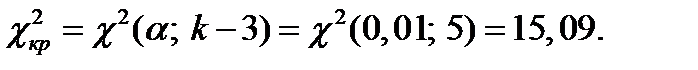
Так как 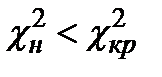 , то нет оснований отвергать проверяемую гипотезу
, то нет оснований отвергать проверяемую гипотезу 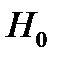 о том, что исходные данные подчиняются нормальному закону распределения.
о том, что исходные данные подчиняются нормальному закону распределения.
Дата: 2019-03-05, просмотров: 1048.