Основные понятия
Гипотезой называют любое предположение о виде или свойствах распределения наблюдаемых в эксперименте случайных величин.
Простой называют гипотезу, содержащую только одно предположение. Сложная гипотеза состоит из нескольких простых гипотез.
Статистическая проверка гипотез осуществляется в 5 этапов по следующей схеме.
Этап 1. Выдвигают предположение – нулевую гипотезу 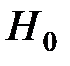 .
.
Этап 2. Задают величину уровня значимости a.
Это вероятность того, что будет допущена ошибка первого рода, т.е. будет отвергаться правильная гипотеза 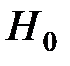 .
.
Этап 3. Для каждой гипотезы 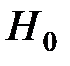 должен быть разработан (обоснован математически) статистический критерий (решающее правило), как функция от результатов наблюдений
должен быть разработан (обоснован математически) статистический критерий (решающее правило), как функция от результатов наблюдений 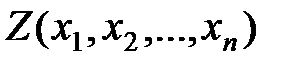 .
.
Функция Z, как и всякая функция от результатов наблюдений, сама является случайной величиной и в предположении о справедливости гипотезы 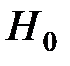 подчинена некоторому хорошо изученному (обычно заданному в форме таблицы) закону распределения с плотностью f(z).
подчинена некоторому хорошо изученному (обычно заданному в форме таблицы) закону распределения с плотностью f(z).
Всю область значений СВ Z можно разбить на три части (рис. 2.1):
1 – область неправдоподобно малых значений критерия ( 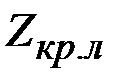 );
);
2 – область естественных (или вероятных) значений, т.е. область принятия гипотезы 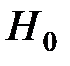 ;
;
3 – область неправдоподобно больших значений ( 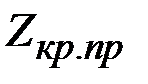 ).
).
Этап 4. Вычисляют критические точки 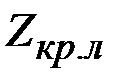 ,
, 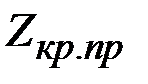 в зависимости от
в зависимости от 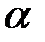 , числа опытов n, вида функции Z, а также с учётом того, какую основную опасность (гипотеза
, числа опытов n, вида функции Z, а также с учётом того, какую основную опасность (гипотеза 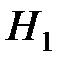 ) для утверждения
) для утверждения 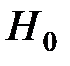 представляют отклонения Z (слишком малые; слишком большие; и те, и другие) – совокупность значений критерия, при которых гипотезу
представляют отклонения Z (слишком малые; слишком большие; и те, и другие) – совокупность значений критерия, при которых гипотезу 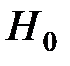 отбрасывают.
отбрасывают.
Суммарная площадь критической (заштрихованной) области равна 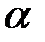 . В случае двухсторонней критической области левую и правую части определяют, исходя из условия равенства их площадей величине
. В случае двухсторонней критической области левую и правую части определяют, исходя из условия равенства их площадей величине 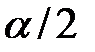 .
.
Наиболее часто используются критерии, приводящие либо к нормальному распределению, либо к распределению 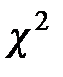 , либо к Т – распределению Стьюдента, либо к F–распределению Фишера.
, либо к Т – распределению Стьюдента, либо к F–распределению Фишера.
В этих случаях критические точки определяются с использованием таблиц квантилей соответствующих распределений следующим образом (табл. 2.1).
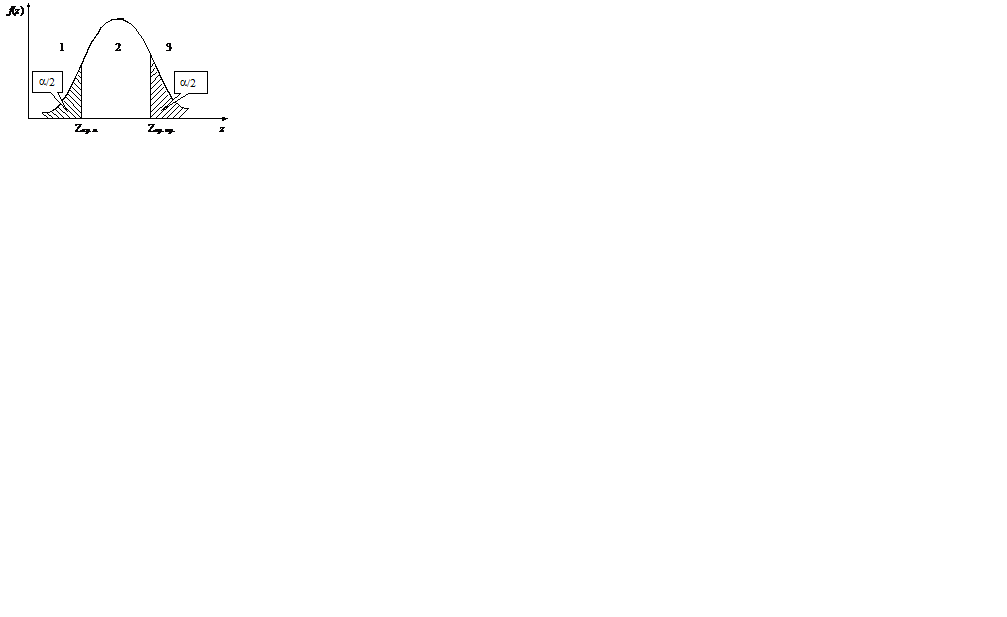
|
Рис. 2.1. Двухсторонняя критическая область критерия
Таблица 2.1
Вычисление критических точек для различных распределений
| Распределение (используемая таблица) | Левосторонняя критическая область | Правосторонняя критическая область | Двухсторонняя критическая область |
| Нормальное (функция Лапласа) | 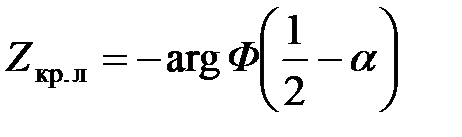
| 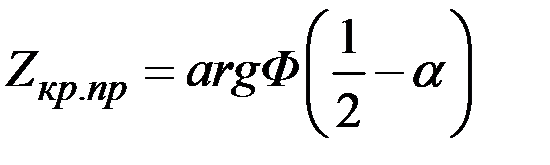
| 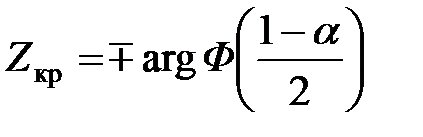
|
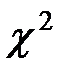 – распределение
(квантили – распределение
(квантили 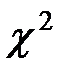 – распределения) – распределения)
|
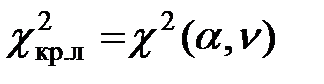
|
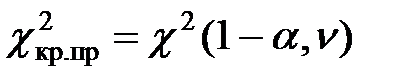
| 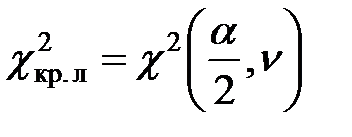 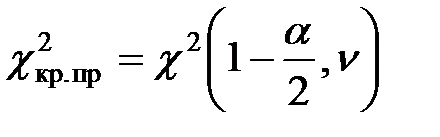
|
| Т–распределение Стьюдента | 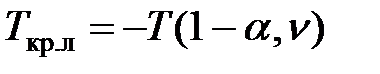
| 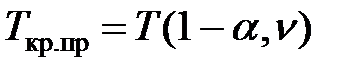
| 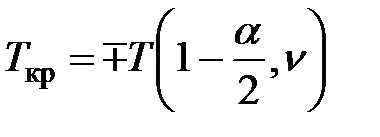
|
| F–распределение Фишера |
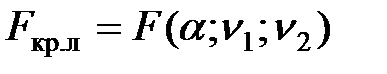
|
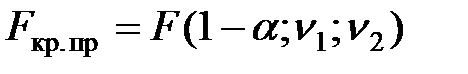
| 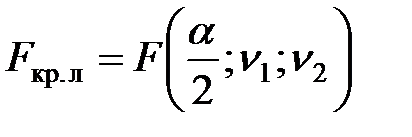 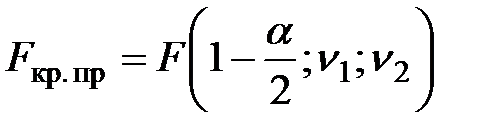
|
Этап 5. В функцию Z подставляют имеющиеся конкретные выборочные данные и подсчитывают численное значение 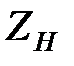 .
.
Если окажется, что это значение 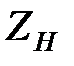 принадлежит области вероятных значений Z (т.е. области 2), то гипотеза
принадлежит области вероятных значений Z (т.е. области 2), то гипотеза 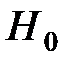 с вероятностью
с вероятностью 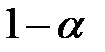 считается не противоречащей исходным данным наблюдения.
считается не противоречащей исходным данным наблюдения.
В противном случае делают вывод, что Z на самом деле не подчиняется закону f(z) (вероятность ошибки этого вывода равна 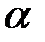 ).
).
Следовательно, гипотеза 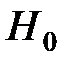 является несостоятельной, её отбрасывают и принимают конкурирующую гипотезу
является несостоятельной, её отбрасывают и принимают конкурирующую гипотезу 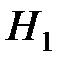 .
.
Можно по наблюдаемому значению критерия 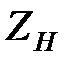 и по соответствующим таблицам f(z) определить вероятность того, что значение
и по соответствующим таблицам f(z) определить вероятность того, что значение 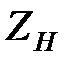 обусловлено за счёт чисто случайных причин.
обусловлено за счёт чисто случайных причин.
Если эта вероятность малой не является, то делается вывод о непротиворечивости исходных данных гипотезе 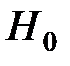 .
.
Примечание. При проверке гипотез могут быть допущены ошибки двух родов (рис.2.2).

Рис.2.2. Ошибки первого и второго рода при проверке гипотезы
Ошибка первого рода (уровень значимости a) – это вероятность того, что будет отвергаться правильная нулевая гипотеза 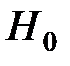 .
.
Ошибка второго рода состоит в том, что будет принята неправильная нулевая гипотеза.
Вероятность ошибки второго рода обычно обозначают через b.
Мощностью критерия называют вероятность попадания критерия в критическую область при условии, что справедлива конкурирующая гипотеза. Это вероятность того, что нулевая гипотеза будет отвергнута, если верна конкурирующая гипотеза 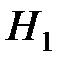 .
.
Смысл параметров α и β при проверке гипотез можно наглядно продемонстрировать на примере заседания суда.
Суд на основании представленных данных должен вынести решение (проверить нулевую гипотезу Н0: обвиняемый не виновен; гипотеза Н1: обвиняемый виновен) о виновности или невиновности подсудимого.
Решение суда и действительность могут не совпадать в зависимости от представленных данных (доказательств):
|
Решение суда | Действительность | |
| Гипотеза Н0 верна | Гипотеза Н0 ложна | |
| Гипотеза Н0 принята (подсудимый освобождён) | β | |
| Гипотеза Н0 отвергнута, принята конкурирующая гипотеза Н1 (подсудимый осуждён) | α | |
Критерии согласия (тесты) бывают двух классов: параметрические и непараметрические.
Непараметрические критерии (критерии, свободные от распределения) используются для статистической проверки гипотез, когда закон распределения исходной генеральной совокупности неизвестен.
Например, при проверке гипотезы о совпадении средних двух выборок можно предположить, что исходная генеральная совокупность имеет нормальное распределение. Тогда соответствующий (параметрический) критерий будет критерием Стьюдента.
Если же закон распределения генеральной совокупности неизвестен, то критерием проверки станет непараметрический критерий Вилкоксона.
Ниже приведены некоторые наиболее часто встречающиеся основные гипотезы и соответствующие критерии их проверки.
Дата: 2019-03-05, просмотров: 375.