Пример 1.10. Имеются следующие данные о распределении населения города по среднедушевому денежному доходу:
| Среднедушевой доход в месяц, у.е., xi | Численность населения, тыс. чел., ni | Середина интервала, xi | xi n i | Кумулятивная частота, nx |
| До 100 | 2,9 | 50 | 145 | 2,9 |
| 100 – 200 | 18,5 | 150 | 2775 | 21,4 |
| 200 – 300 | 25,5 | 250 | 6375 | 46,9 |
| 300 – 400 | 23,4 | 350 | 8190 | 70,3 |
| 400 – 500 | 18,8 | 450 | 8460 | 89,1 |
| 500 – 600 | 14,3 | 550 | 7865 | 103,4 |
| 600 – 700 | 10,7 | 650 | 6955 | 114,1 |
| 700 – 800 | 8 | 750 | 6000 | 122,1 |
| 800 – 900 | 6 | 850 | 5100 | 128,1 |
| 900 – 1000 | 4,5 | 950 | 4275 | 132,6 |
| 1000 – 1100 | 3 | 1050 | 3150 | 135,6 |
| 1100 – 1200 | 3 | 1150 | 3450 | 138,6 |
| 1200 – 1300 | 1,7 | 1250 | 2125 | 140,3 |
| 1300 – 1400 | 1,8 | 1350 | 2430 | 142,1 |
| Свыше 1400 | 6,1 | 1450 | 8845 | 148,2 |
| Итого | 148,2 | 76140 |
Определить: среднедушевой месячный доход; нижний и верхний децили; децильный коэффициент дифференциации доходов населения.
Решение. Среднедушевой месячный денежный доход равен
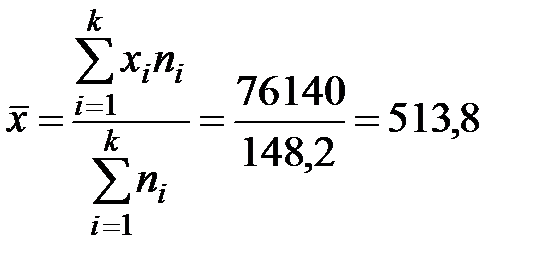у.е.
Нижний и верхний децили исчисляют по формуле медианы.
В этом случае вместо медианного интервала используют интервалы с номером j, в которых находятся варианты, отсекающие по 10% численности частот в разных концах ряда распределения.
Первый дециль (самые низкие доходы) определяется по формуле:
.
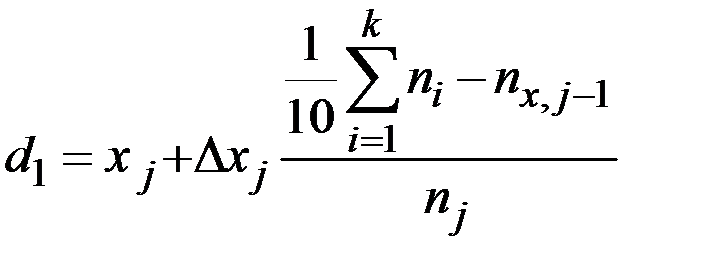Для расчёта первого (нижнего) дециля находим 1/10 численности частот:
.
По накопленным частотам видно, что вариант, соответствующий такой частоте, находится во втором интервале (j = 2) денежных доходов (100 – 200 у.е.).
Тогда
.
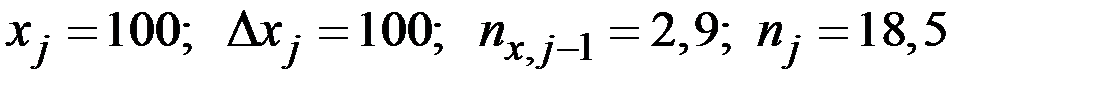Отсюда граница самых низких доходов:
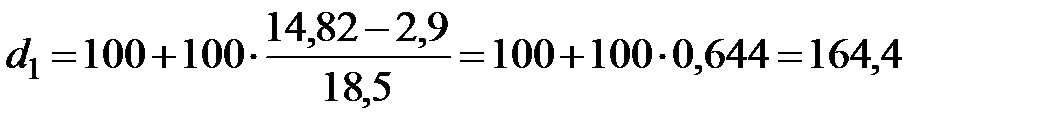у.е.
Верхний дециль определяется по формуле
.
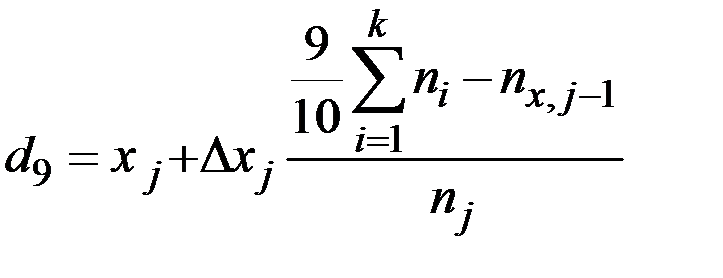Для расчёта девятого (верхнего) дециля находим 9/10 численности частот:
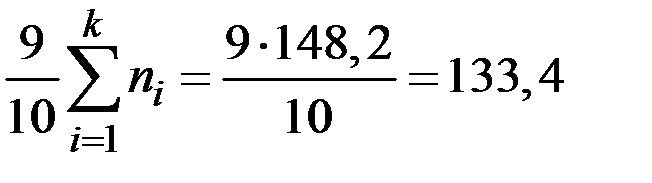тыс. чел.
По накопленным частотам видно, что вариант, соответствующий такой частоте, находится в интервале 1000 – 1100 у.е. (j = 12).
Тогда
.
Отсюда граница самых высоких доходов:
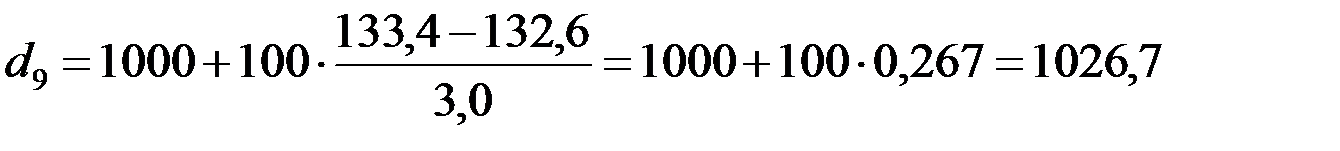у.е.
Децильный коэффициент дифференциации доходов населения составляет величину
.
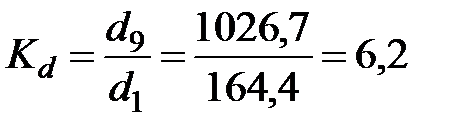Децильный коэффициент дифференциации доходов населения показывает, что среднедушевой доход, выше уровня которого имели доход 10% населения (высокодоходная группа), в анализируемом году превышал в 6,2 раза уровень дохода, ниже которого имели доход 10% населения (низкодоходная группа).
Пример 1.11. По схеме собственно случайной выборки из 1800 изготовленных одинаковых приборов было отобрано 200. Получено следующее распределение их по продолжительности работы (в месяцах):
Продолжительность
работы (месяцы) 
| (33 – 34] | (34 – 35] | (35 – 36] | (36 – 37] | (37 – 38) |
Число приборов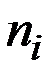 
| 8 | 10 | 89 | 60 | 33 |
Определить:
1) границы, в которых с вероятностью 0,99 заключена средняя продолжительность работы прибора во всей партии;
2) границы, в которых с вероятностью 0,99 заключена продолжительность работы произвольного прибора во всей партии;
3) вероятность того, что доля приборов в выборке с продолжительностью работы до первой поломки не более, чем 35 месяцев, отличается от доли таких приборов во всей партии не больше, чем на 0,01 (по абсолютной величине).
Решение. Пусть случайная величина Х – продолжительность работы прибора. Примем обозначения: Рд – доверительная вероятность; n – объём выборки; N – объём генеральной совокупности; L – количество интервалов группировки исходного показателя Х.
Из условия задачи имеем Pд = 0,99; n = 200; N = 1800.
Вычислим выборочные среднее значение продолжительности работы одного прибора, дисперсию и СКО продолжительности работы.
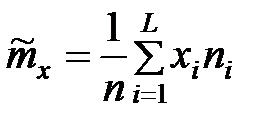= (33,5Ч8 + 34,5Ч10 + 35,5Ч89 + 36,5Ч60 + 37,5Ч33)/200 = 36.
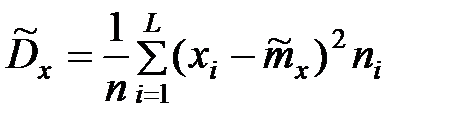=Ч((33,5 – 36)2Ч8 + (34,5 – 36)2Ч10 + (35,5 – 36)2Ч89 +
+ (36,5 – 36)2Ч60 + (37,5 – 36)2Ч33)/200 = 0,92.
.
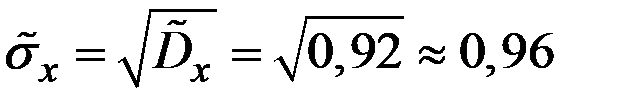Тогда дисперсия средней продолжительности работы одного прибора определяется (с учётом бесповторности выборки) по формуле
.
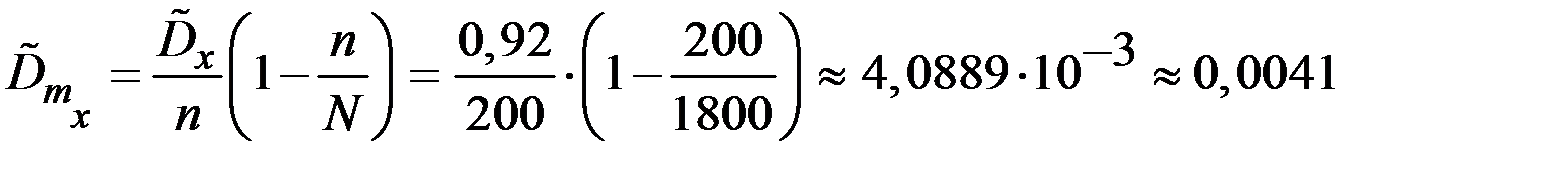Соответствующее среднее квадратичное отклонение имеет значение
.
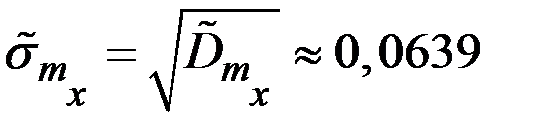1. Доверительные границы, в которых с вероятностью Рд заключено среднее время продолжительности работы одного прибора во всей партии, определяется по соотношению
,
где tф = arg Ф(Рд /2) – аргумент функции Лапласа.
По таблице функции Лапласа находим
tф = argФ(0,99/2) = argФ(0,495) » 2,58.
Тогда границы доверительного интервала будут следующими:
a1 = 36 – 2,58Ч0,0639 = 35,835;
a2 = 36 + 2,58Ч0,0639 = 36,165.
Таким образом, с вероятностью 0,99 можно утверждать, что средняя продолжительность работы прибора во всей партии заключается в пределах от 35,835 до 36,165 месяцев.
2. Доверительные границы, в которых с вероятностью Рд заключено время продолжительности работы одного (произвольно взятого) прибора во всей партии, определяется по соотношению
3. Выборочная доля приборов с продолжительностью работы до первой поломки не более, чем 35 месяцев, составляет величину
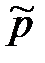= (8 + 10)/200 = 0,09.
Вероятность того, что доля всех таких приборов отличается от выборочной доли не более, чем на величину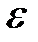 
= 0,01 (по абсолютной величине) определяется также с использованием функции Лапласа:
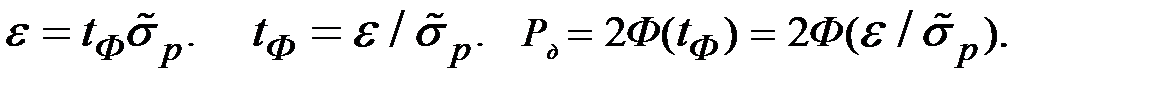
Среднее квадратичное отклонение доли
.
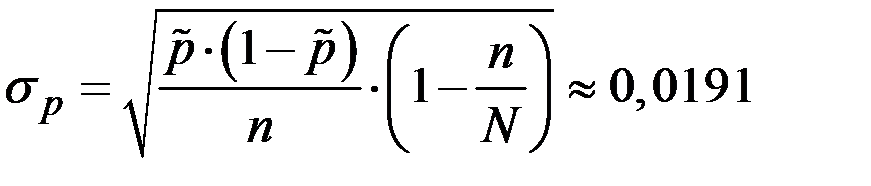Тогда искомая вероятность
Pд = 2ЧФ(0,01/0,0191) = 2ЧФ(0,524) » 2Ч0,1985 = 0,397.
То есть, с вероятностью 0,397 можно утверждать, что доля всех приборов с продолжительностью работы до первой поломки не более 35 месяцев отличается от их доли в выборке не больше, чем на 0,01 (т.е. находится в пределах от 0,08 до 0,1).
Пример 1.12. Рассчитать необходимую численность выборки для определения доли заказных писем, отправляемых на почтамте государственными организациями, если доверительная вероятность равна 0,954, а предельная ошибка доли должна составлять 0,025. Никаких предварительных данных об удельном весе этих писем в общей массе заказной корреспонденции, равной 5000 писем, не имеется. Решить задачу при проведении: а) повторной выборки; б) бесповторной выборки.
Решение. Предельная ошибка выборочной доли повторной выборки выражается формулой
,
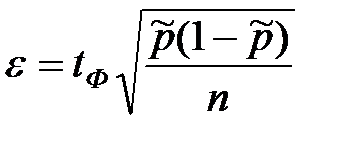а для бесповторной выборки
.
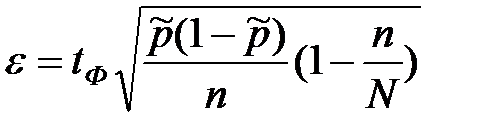Имеем N = 5000, 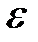= 0,025.
Необходимо найти n.
Значение tФ определим по таблице значений функции Лапласа:
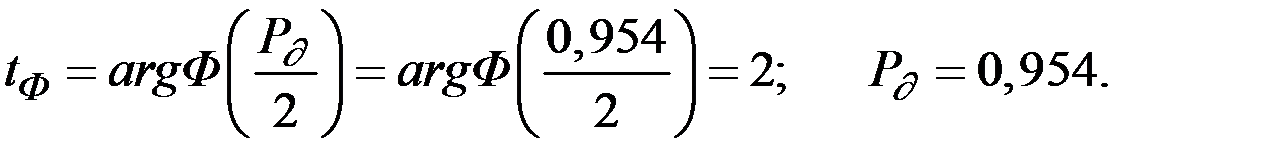
Наша цель – определить n для обоих случаев.
Получим:
а) 
для повторной выборки;
б)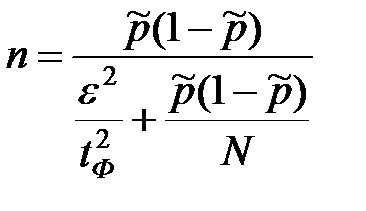 
для бесповторной выборки.
Значение n определим для наихудшего случая (по максимальному значению в зависимости от ).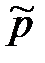
Наибольшее значение выражения 
будет при 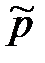= 0,5.
Тогда для повторной выборки:
;
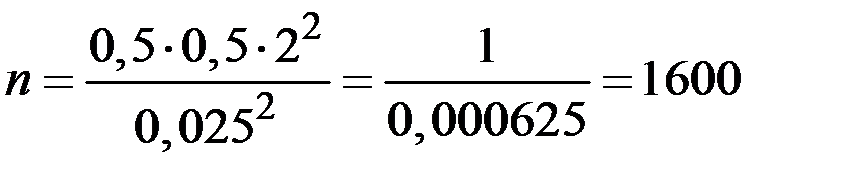для бесповторной выборки:
.
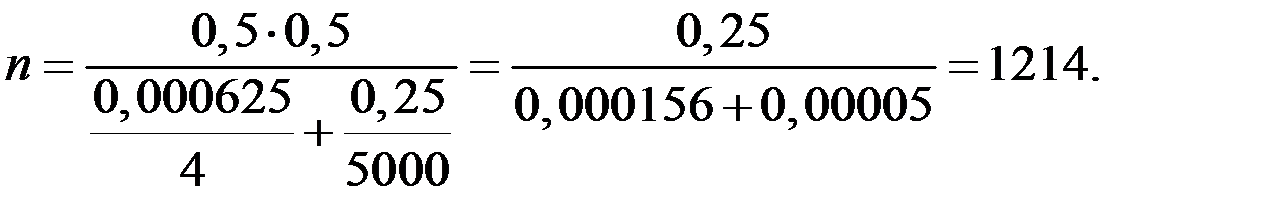Пример 1.13. Определить необходимую численность выборки при обследовании остатков на расчётных счетах у клиентов коммерческого банка, чтобы с вероятностью 0,683 ошибка репрезентативности не превышала 5 тыс. руб., если известно, что среднее квадратическое отклонение остатков составляет 120 тыс. руб.
Решение. Предположим, что выборка повторная.
Находим коэффициент доверия (аргумент функции Лапласа)
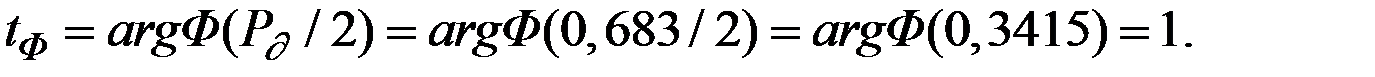
Тогда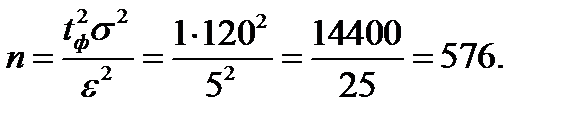 
Пример 1.14. В n независимых опытах событие А произошло m раз. Найти оценку неизвестной вероятности Р появления события А в каждом опыте методом максимального правдоподобия.
Решение. Функция правдоподобия для распределения Бернулли принимает вид:
.
Тогда
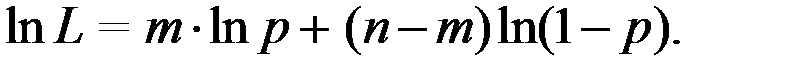
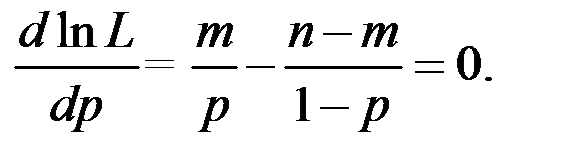
Отсюда
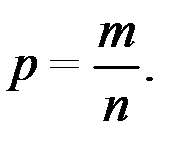
Пример 1.15. Средняя зарплата в фирме составляет 20 тыс. рублей в месяц, а среднее квадратическое отклонение зарплаты равно 5 тыс. рублей в месяц. Каков диапазон зарплаты у 90% работников фирмы?
Решение. Можно предположить нормальный закон у зарплаты.
Найдём предельную ошибку:
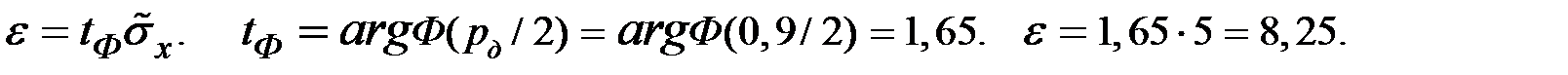
Тогда диапазон зарплаты у 90% работников фирмы:
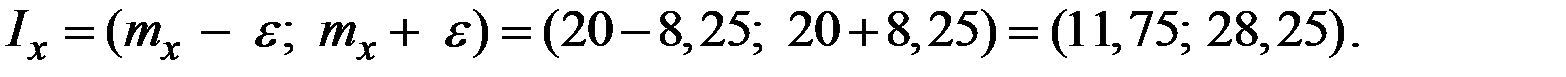
Пример 1.16. Провели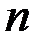 
опытов. Методом максимального правдоподобия найти оценки параметров нормального закона.
Решение. Нормальный закон имеет вид:
.
Функция правдоподобия определяется формулой:
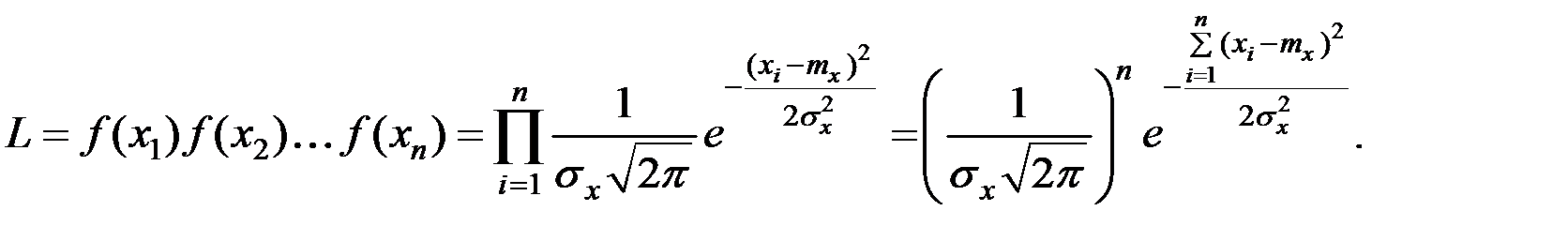
Прологарифмируем функцию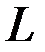 
.
Получим:
Решим систему уравнений:
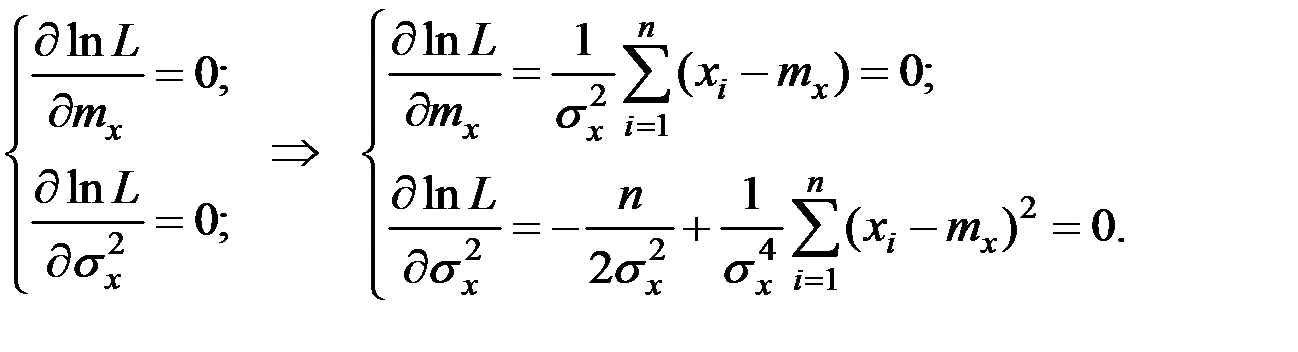
Отсюда получаем:
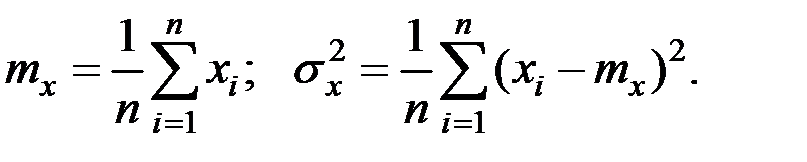
Пример 1.17. Проверили качество изделий в 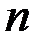упаковках. В 
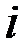–ой упаковке 
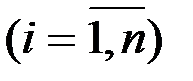было обнаружено 
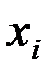бракованных изделий. Предполагая, что число бракованных изделий в упаковке подчиняется закону Пуассона, определить его параметр методом максимального правдоподобия.
Решение. Закон Пуассона запишем в виде:
,
где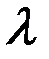 
− параметр закона Пуассона, который необходимо определить,
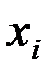
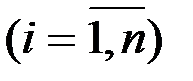− число появлений события в 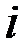– ом опыте.
Составим функцию правдоподобия:
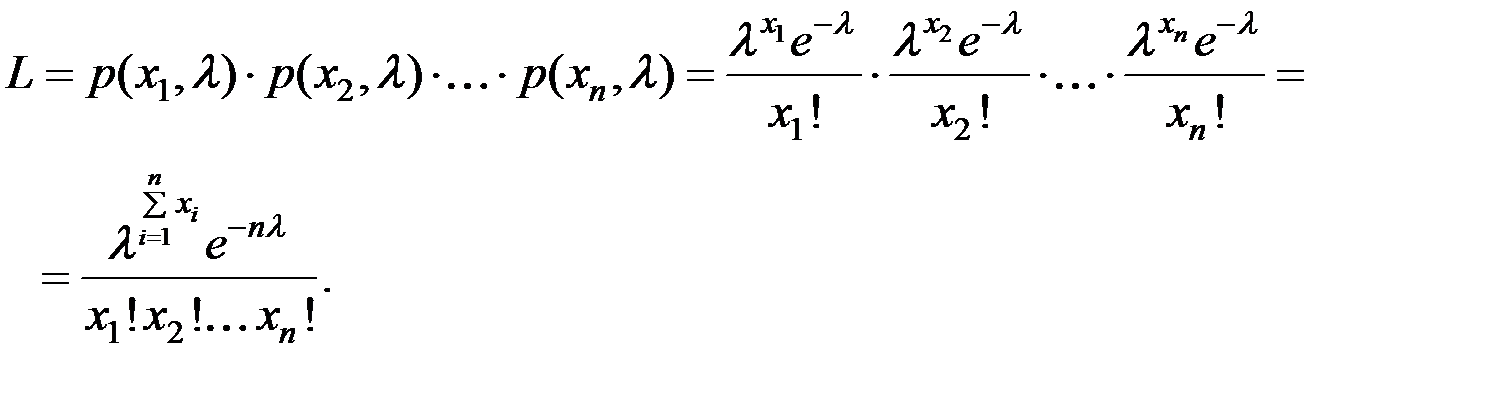
Найдём логарифмическую функцию правдоподобия:
.
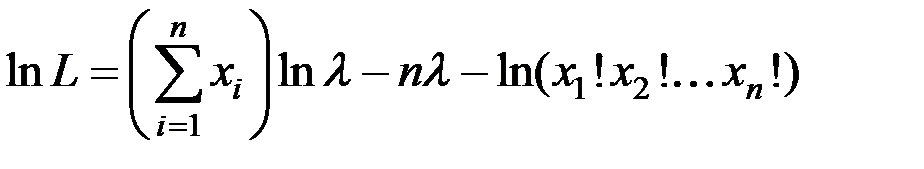Найдём первую производную по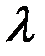 
:
.
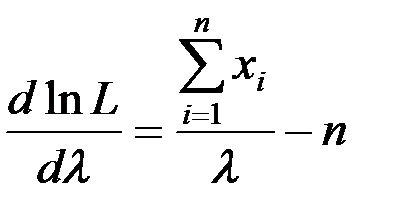Запишем уравнение правдоподобия, для чего приравняем первую производную нулю:
Решим уравнение относительно :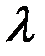
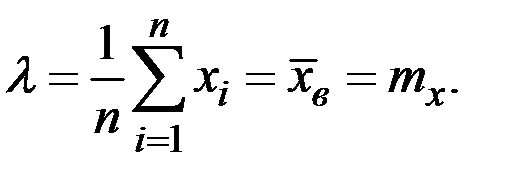
Найдём вторую производную по :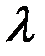
.
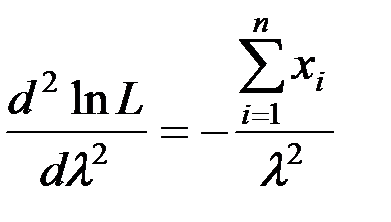Легко видеть, что при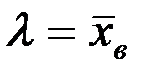 
вторая производная отрицательна; следовательно, 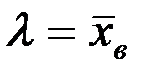есть точка максимума и значит, в качестве оценки наибольшего правдоподобия параметра 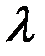распределения Пуассона надо принять выборочную среднюю
.
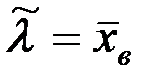Пример 1.18. По выборке из n = 15 студентов группы определены средний рост студента группы, дисперсия и СКО этого роста. Получены следующие результаты:
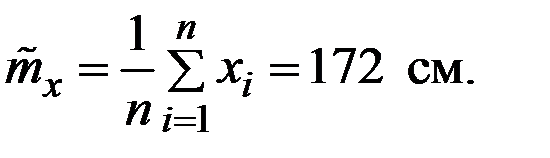
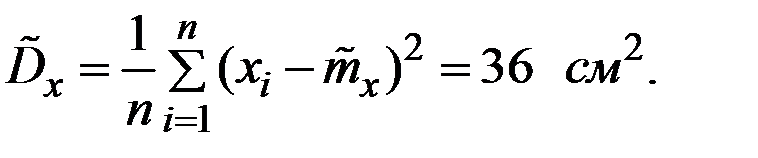
Определить доверительные интервалы для среднего роста студента института (в котором учатся N = 600 студентов) и для произвольно взятого студента института с доверительной вероятностью 0,95.
Решение. Дисперсия среднего роста студента института (с учётом бесповторности выборки) вычисляется по формуле
.
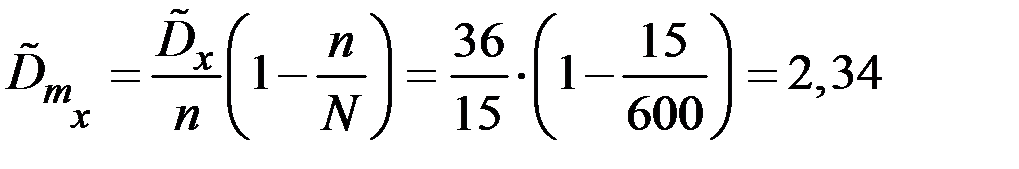Соответствующее среднее квадратичное отклонение равно (см)
.
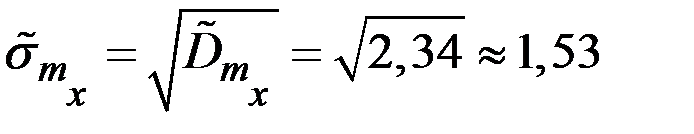Доверительные границы, в которых с вероятностью Рд заключён средний роста студента института, определяется по соотношению
.
По таблице функции Лапласа:
tф = argФ(0,95/2) = argФ(0,475) » 1,96.
Тогда границы доверительного интервала будут следующими:
a1 = 172 – 1,96Ч1,53 = 169 см;
a2 = 172 + 1,96Ч1,53 = 175 см.
Таким образом, с вероятностью 0,95 можно утверждать, что средний рост студента института заключается в пределах от 169 см до 175 см.
Доверительные границы, в которых с вероятностью Рд заключён рост произвольно взятого студента института, определяется по соотношению
.
Тогда границы доверительного интервала будут следующими:
a1 = 172 – 1,96Ч6 = 160,26 см;
a2 = 172 + 1,96Ч6 = 183,76 см.
C вероятностью 0,95 можно утверждать, что рост произвольно взятого студента института заключается в пределах от 160,26 см до 183,76 см.
Пример 1.19. По случайной выборке из 46 студентов института (в котором обучается 680 студентов) подсчитали, что среднее число баллов у выбранных студентов по всем 5 экзаменам сессии составляет 280, среднее квадратическое отклонение баллов составило 53 балла. С вероятностью 0,95 определить доверительные интервалы для среднего количества баллов у студентов всего института и для количества баллов у произвольно взятого студента института.
Решение. Пусть Х – количество баллов у студента института.
Из условия задачи имеем Pд = 0,95; n = 46; N = 680.
Имеем выборочные среднее значение количества баллов студентов из выборки и СКО количества баллов у них.
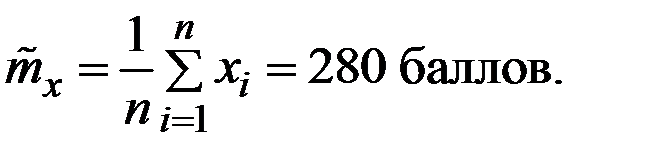
Тогда дисперсия среднего количества баллов у студентов всего института (с учётом бесповторности выборки) вычисляется по формуле
.
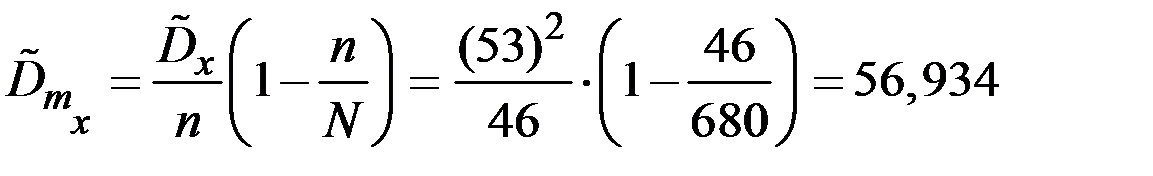Соответствующее среднее квадратичное отклонение
.
Доверительный интервал для среднего количества баллов у студентов всего института определяется по соотношению
,
где tф = arg Ф(Рд /2) – аргумент функции Лапласа.
По таблице функции Лапласа находим
tф = argФ(0,95/2) = argФ(0,475) » 1,96.
Тогда границы доверительного интервала будут следующими:
a1 = 280 – 1,96Ч7,545 = 280 – 14,8 = 265,2.
a2 = 280 + 1,96Ч7,545 = 280 + 14,8 = 294,8.
С вероятностью 0,95 можно утверждать, что среднее количество баллов студента института заключается в пределах от 265,2 до 294,8.
Доверительный интервал для количества баллов у произвольно взятого студента института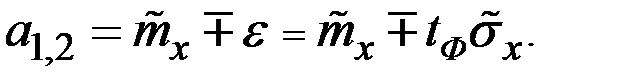 
Получаем: a1 = 280 – 1,96Ч53 = 280 – 103,9 = 176,1.
a2 = 280 + 1,96Ч53 = 280 + 103,9 = 383,9.
С вероятностью 0,95 можно утверждать, что количество баллов произвольно взятого студента института заключается в пределах от 176,1 до 383,9 баллов.
Пример 1.20. Из 40 протестированных деталей с конвейера 4 требовали доработки (обнаружены дефекты по некоторым параметрам). С какой вероятностью можно утверждать, что необходимость доработки произвольно взятой детали с конвейера находится в пределах от 7 до 13 процентов?
Решение. Имеем для точности альтернативного признака параметр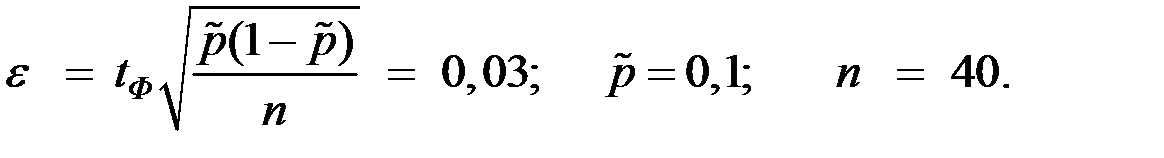 
Найдём сначала значение коэффициента доверия 
а затем и 
.
Получаем
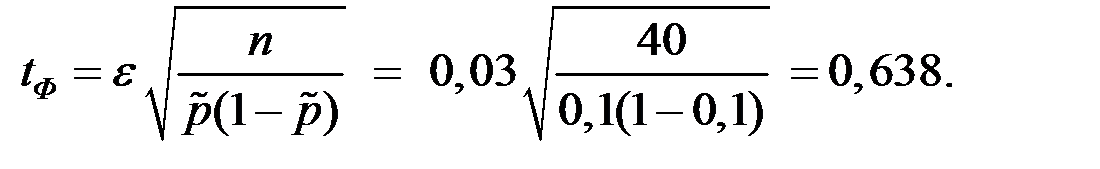
Искомая вероятность
Контрольные вопросы к главе 1
1. Что такое выборочный метод?
2. Охарактеризуйте особенности построения полигона и гистограммы распределения случайной величины по выборке.
3. Как оцениваются ошибки выборочного метода?
4. Поясните условия получения репрезентативной выборки.
5. Что такое вариационный ряд случайной величины?
6. Поясните различие точечных и интервальных оценок параметров.
7. Поясните методику получения закона распределения случайной величины по статистическим данным.
8. Поясните различие и особенности использования методов наименьших квадратов и максимального правдоподобия.
9. Поясните особенности метода моментов и метода квантилей.
10. Укажите виды статистических оценок параметров и их свойства.
11. Поясните смысл доверительных интервалов для параметров.
12. Поясните смысл эффективных, несмещённых и состоятельных оценок неизвестных параметров.
13. Поясните смысл интервальных оценок показателей.
ЗАДАНИЯ ДЛЯ КОНТРОЛЬНОЙ РАБОТЫ № 1
ЗАДАНИЕ 1.1.
По имеющимся данным построить закон распределения заданной случайной величины (см. варианты задания). Необходимо:
1. Получить вариационный ряд исследуемой случайной величины.
2. Произвести табулирование (группировку) данных вариационного ряда на 6 – 8 интервалов (разрядов, групп).
3. Вычислить и представить графически эмпирические функции распределения вероятностей и плотности распределения исследуемой СВ.
4. Выровнять (аппроксимировать) имеющиеся данные подходящим теоретическим законом распределения заданной случайной величины.
5. Проанализировать полученные результаты.
ЗАДАНИЕ 1.2. По имеющимся данным и результатам расчётов, выполненных в работе 1.1, построить доверительные интервалы для математического ожидания, дисперсии и среднего квадратического отклонения заданной случайной величины. Необходимо:
1. Распределение случайной величины взять из задания 1.1.
2. Доверительные интервалы параметров строить с учётом полученного закона распределения случайной величины как точными так и приближёнными методами (там, где это возможно) для различных значений доверительной вероятности (0,9; 0,95; 0,99).
3. Проанализировать полученные результаты.
ЗАДАНИЕ 1.3.
По схеме случайной выборки из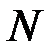 
объектов исследования генеральной совокупности было отобрано 
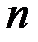. Получено соответствующее распределение анализируемого показателя (см. варианты задания 1).
Необходимо:
1) определить границы, в которых с вероятностью 
заключено среднее значение показателя во всей генеральной совокупности;
2) вычислить вероятность того, что доля объектов исследования в выборке со значением показателя, не меньшим чем среднее значение выборки плюс среднее квадратическое отклонение, отличается от доли таких приборов во всей генеральной совокупности (партии) не больше, чем на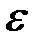 
(по абсолютной величине);
3) рассчитать необходимую численность выборки для определения среднего значения показателя с предельной ошибкой, равной 
;
4) проанализировать полученные результаты.
ВАРИАНТЫ ЗАДАНИЯ
1. Количество сделок (договоров) фирмы по месяцам (ед.): 18, 22, 23, 24, 25, 24, 27, 25, 23, 22, 23, 27, 26, 24, 22, 20, 21, 22, 23, 22, 21, 20, 19, 16, 17, 20, 22, 22, 23, 27, 30, 28, 27, 25, 27, 25, 22, 20, 20, 21, 23, 27, 29, 33, 30, 29, 26, 24, 23, 21, 18, 20, 22, 23, 24, 26.
2. Прибыль фирмы (млн.р./мес.): 8,3; 8,7; 10,3; 10,7; 9,9; 8,6; 8,9; 9,1; 9,9; 9,8; 10,2; 8,9; 9,4; 9,3; 9,2; 9,6; 9,4; 9,3; 9,2; 10,1; 9,1; 10,2; 10,4; 9,0; 8,8; 12,1; 11,3; 10,9; 10,3; 9,8; 10,3; 10,4; 10,9; 10,8; 10,7; 9,3; 11,2; 11,4; 8,2; 12,7; 10,3; 10,8; 10,3; 10,4; 10,9; 10,8, 10,7, 10,5.
3. Рентабельность собственных средств предприятия (%): 22,3; 24,5; 21,8; 19,7; 22,3; 24,1; 22,8; 21,7; 21,5; 20,4; 20,7; 21,5; 21,2; 20,3; 20,8; 21,4; 21,6; 21,9; 22,0; 22,2; 22,8; 19,7; 21,4; 22,9; 22,1; 22,3; 21,6; 21,3; 21,7; 21,1; 22,1.
4. Отклонение от плана нормы выработки рабочего по неделям (%): 0,2; 0,3; 0,1; 0; 0; –0,1; –0,3; –0,1; 0; 0; 0,3; 0,2; 0,1; –0,1; –0,2; –0,3; –0,1; 0; 0,2; 0,1; 0; 0,1; 0; 0; 0; 0,4; 0,3; 0,2; –0,1; 0,1; –0,1; 0,2; 0,3; 0,8; 0,9; 0,5; 0; 0,3; –0,5; –0,6; 0,1; 0; 0,6; 1,5; 0,7; 0,2; 0,1.
5. Выпуск изделий по месяцам (шт.): 32, 30, 28, 27, 24, 25, 27, 32, 29, 28, 27, 22, 20, 22, 25, 24, 26, 25, 20, 18, 19, 26, 25, 24, 26, 25, 33, 35, 30, 28, 27, 27, 23, 19, 20, 27, 28, 30.
6. Валовые издержки предприятия (тыс. р./мес.): 30, 40, 52, 44, 37, 38, 42, 41, 44, 33, 38, 41, 39, 37, 30, 37, 42, 53, 50, 49, 51, 46, 45, 40, 42, 51, 52, 47, 46, 54, 38, 61, 57, 50, 44, 47, 45,46, 45.
7. Месячная прибыль фирмы (тыс.р.): 3,4; 2,8; 7,1; 6,2; 4,4; 4,7; 4,8; 4,9; 5,0; 5,1; 3,8; 3,9; 4,7; 4,6; 4,5; 5,7; 5,8; 6,3; 6,4; 5,9; 7,7; 6,2; 4,4; 5,6; 5,0; 6,0; 7,0; 5,8; 6,1; 5,8; 6,4; 6,3; 6,0; 6,9; 6,1; 6,2; 4,8; 4,7.
8. Величина основных фондов предприятия (млн. р.): 60, 70, 82, 91, 99, 103, 100, 85, 74, 63, 84, 76, 87, 88, 89, 90, 93, 96, 91, 99, 81, 77, 67, 71, 68, 70, 76, 81, 96, 96, 93, 84, 96, 99, 102, 105, 100, 98, 84, 77, 85, 83.
9. Урожайность пшеницы (ц/га): 21,3; 21,4; 20,6; 20,8; 22,4; 23,8; 19,3; 17,4; 18,9; 21,4; 22,8; 22,6; 23,1; 22,9; 19,4; 19,7; 20,5; 20,6; 20,7; 21,0; 22,0; 21,8; 20,9; 20,0; 21,4; 23,0.
10. Прибыль фирмы от активов (% за квартал): 3,1; 3,7; 6,4; 3,8; 4,2; 3,0; 3,2; 3,7; 3,0; 3,1; 3,6; 4,1; 4,8; 5,5; 3,0; 3,1; 3,2; 3,0; 3,7; 3,5; 3,1; 3,2; 3,0; 3,1; 3,0; 3,4; 3,5; 3,6; 4,1; 3,7; 4,2; 3,8; 4,6; 4,7; 5,1; 5,8; 3,1; 3,0; 5,4; 6,0; 6,2; 3,0; 3,2; 3,4; 3,5; 3,3; 3,3; 3,0; 4,0.
11. Месячная рентабельность предприятия (%): 19,7; 20,4; 22,8; 20,7; 21,2; 20,3; 20,4; 20,3; 20,7; 22,1; 22,7; 19,1; 21,2; 21,7; 21,2; 21,4; 21,6; 20,4; 20,5; 21,7; 21,0; 20,6; 20,8; 20,9; 22,0; 19,7; 20,1; 23,0; 20,4; 22,3; 22,7; 21,4; 21,5.
12. Валовая продукция цеха (тыс. р./мес.): 160, 172, 168, 173, 174, 169, 171, 172, 170, 171, 168, 164, 158, 172, 171, 170, 166, 164, 162, 161, 161, 168, 170, 170, 163, 162, 161, 167, 164, 167, 158, 159, 171, 170, 164, 160, 163, 165, 166, 166, 156, 170, 164.
13. Месячные объёмы продаж продукции (тыс. р.): 770, 692, 614, 781, 680, 730, 654, 642, 686, 672, 791, 703, 574, 688, 608, 630, 650, 644, 666, 682, 599, 704, 710, 720, 656, 642, 610, 670, 594, 600, 700, 680, 676, 647, 662, 641, 634, 690.
14. Средняя выработка на одного рабочего в фирме по месяцам (тыс. долл.): 66, 60, 64, 69, 72, 80, 84, 78, 74, 70, 53, 58, 60, 66, 67, 60, 64, 33, 47, 65, 64, 77, 56, 54, 65, 55, 51, 48, 66, 67, 60, 55, 52, 57, 43.
15. Товарооборот на душу населения (тыс. р.): 0,9; 0,8; 0,6; 0,4; 0,5; 0,6; 0,7; 0,8; 0,4; 0,9; 0,8; 0,7; 0,9; 1,2; 1,1; 1,0; 0,7; 1,0; 1,4; 1,3; 1,2; 1,4; 0,8; 0,7; 0,9; 0,3, 0,9, 0,8, 0,7.
16. Месячный процент премии на предприятии (%): 15, 16, 18, 20, 20, 25, 27, 28, 22, 18, 16, 15, 23, 26, 28, 15, 23, 26, 28, 16, 18, 21, 23, 25, 25, 22, 18, 16, 20, 19, 18, 16, 21, 23, 26, 28, 30, 32.
17. Запасы продукции на складе по месяцам (тыс.р.): 10,8; 10,4; 17,3; 20,1; 15,3; 23,7; 14,2; 12,1; 11,3; 12,0; 18,4; 13,4; 18,3; 14,7; 16,0; 17,9; 16,2; 16,4; 15,8; 19,3; 18,6; 8,8; 10,1; 9,4; 9,7; 19,4; 20,2; 25,4; 24,3; 20,9; 23,1; 9,1; 9,4; 20,8; 21,2; 22,1; 11,4.
18. Коэффициент ритмичности работы цеха по сменам: 0,62; 0,71; 0,64; 0,79; 0,54; 0,59; 0,64; 0,70; 0,82; 0,67; 0,69; 0,71; 0,81; 0,74; 0,70; 0,72; 0,60; 0,84; 0,76; 0,78; 0,69; 0,66; 0,60; 0,80; 0,58; 0,56.
19. Себестоимость добычи одной тонны руды по месяцам (руб.): 10,5; 10,2; 10,7; 10,4; 10,3; 10,7; 10,6; 10,2; 10,3; 10,5; 10,4; 10,7; 10,4; 10,5; 10,6; 10,4; 10,1; 10,3; 10,2; 10,1; 10,5; 10,5; 10,4; 10,3; 10,7; 10,6; 11,0; 10,8; 10,7; 10,0; 10,5; 11,1; 10,3; 10,4; 10,6; 10,5; 10,5; 10,6; 10,7; 10,5; 10,4; 10,2.
20. Средняя выработка на одного рабочего в фирме по декадам (тыс. р.): 83, 70, 64, 69, 72, 80, 84, 78, 74, 70, 53, 58, 60, 66, 67, 60, 64, 33, 47, 65, 84, 77, 56, 54, 55, 51, 48, 66, 67, 60, 40.
21. Месячная выручка от реализации продукции (тыс. р.): 570, 592, 604, 581, 680, 730, 654, 642, 686, 672, 591, 703, 574, 688, 608, 630, 650, 644, 666, 682, 599, 704, 710, 520, 656, 642, 610, 670, 594, 600, 700, 680, 676, 647, 662, 641, 634, 690.
22. Себестоимость производства детали по месяцам (руб.): 11,4; 11,3; 10,7; 10,6; 10,4; 10,7; 10,4; 10,5; 10,6; 10,4; 10,1; 10,3; 10,2; 10,1; 11,5; 10,5; 11,4; 10,3; 10,7; 10,6; 11,0; 10,8; 10,7; 10,0; 10,5; 11,1; 10,3; 10,4; 10,6; 11,5; 10,5; 10,6; 10,7; 11,5; 10,4; 11,2.
23. Месячное потребление электроэнергии (квт. час): 171, 183, 199, 185, 183, 177, 179, 181, 188, 179, 177, 179, 180, 182, 190, 179, 174, 172, 166, 167, 170, 171, 172, 175, 178, 181, 188, 180, 174, 175, 175, 166, 168, 171, 176, 175, 174, 171, 173, 186, 180, 178, 197, 193, 185, 176.
24. Себестоимость производства детали по месяцам (руб.): 11,4; 11,3; 10,7; 10,6; 10,4; 10,7; 10,4; 10,5; 10,6; 10,4; 10,1; 10,3; 10,2; 10,1; 11,5; 10,5; 11,4; 10,3; 10,7; 10,6; 11,0; 10,8; 10,7; 10,0; 10,5; 11,1; 10,3; 10,4; 10,6; 11,5; 10,5; 10,6; 10,7; 11,5; 10,4; 11,2.
Дата: 2019-03-05, просмотров: 440.
