Пусть 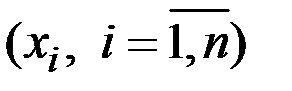 – выборка из значений случайной величины X;

f(x, a) – плотность распределения СВ с параметром а (для непрерывных величин);

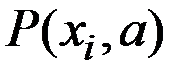– вероятность того, что величина примет значение  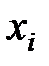(для дискретных СВ).

Функция правдоподобия для непрерывной случайной величины определяется формулой

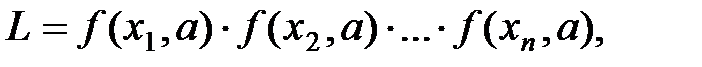
а для дискретной СВ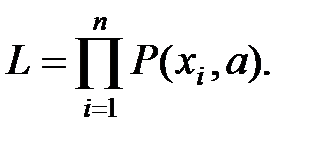

Сущность метода максимального правдоподобия состоит в том, что в качестве оценки параметра a берётся значение, обращающее функцию L в максимум.

Для нахождения оценки a нужно решить уравнение

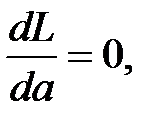
принимая 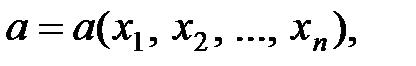 которое обращает L в максимум.

В ряде случаев вместо L удобнее рассматривать функцию ln(L) и решать уравнение     .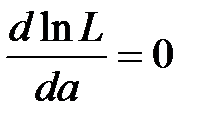

В случае двух параметров ( 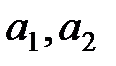) их оценки находятся решением системы двух уравнений         

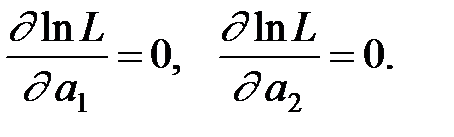
Пример 1.8. Провели n наблюдений за временем обслуживания одного клиента в фирме. Получили n значений СВ: 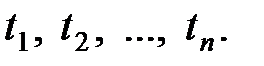 Определить закон распределения времени обслуживания одного клиента в данной фирме, используя метод максимального правдоподобия.

Решение. Из физической сути явления следует (можно предположить), что время обслуживания одного клиента t подчинено экспоненциальному закону: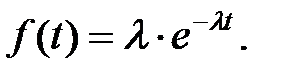

Необходимо определить параметр .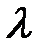

Для этого составим функцию правдоподобия

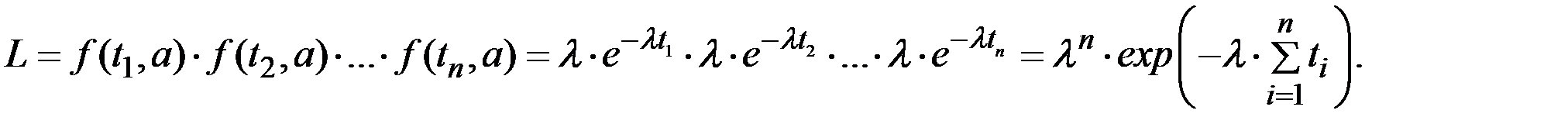
Для удобства рассмотрим логарифмическую функцию правдоподобия экспоненциального закона распределения

.

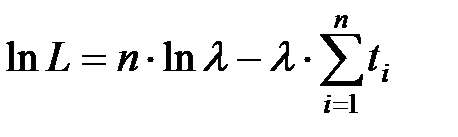Параметр 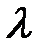 найдём из уравнения:  

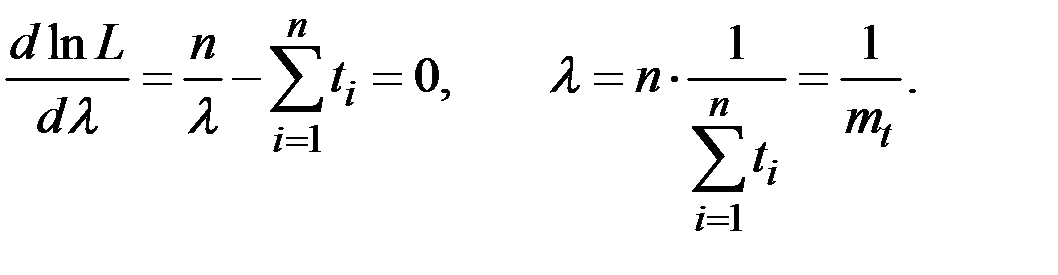
Пример 1.9. Для определения неизвестной вероятности Р появления события А в каждом опыте производится две серии из n₁ и n₂ независимых опытов, причём в первой серии событие А произошло m₁ раз, а во второй серии – m₂ раза. Определить искомую вероятность Р методом максимального правдоподобия.

Решение. Вероятность того, что в серии из n₁ опытов событие А произойдёт ровно m₁ раз определяется по биномиальному закону

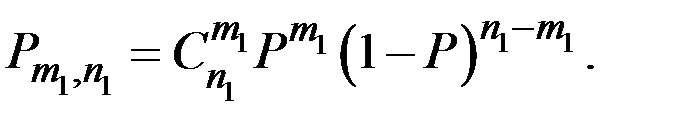
Аналогично, вероятность того, что в серии из n₂ опытов событие А произойдёт ровно m₂ раза определяется по закону

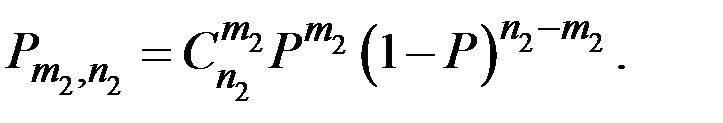
Тогда функция правдоподобия для задачи принимает вид:

.

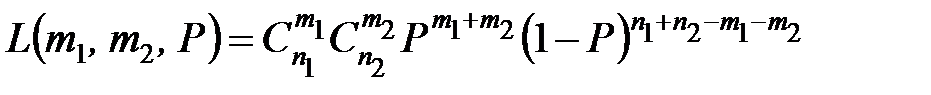Логарифмируя эту функцию и приравнивая к нулю производную по неизвестному параметру получим :

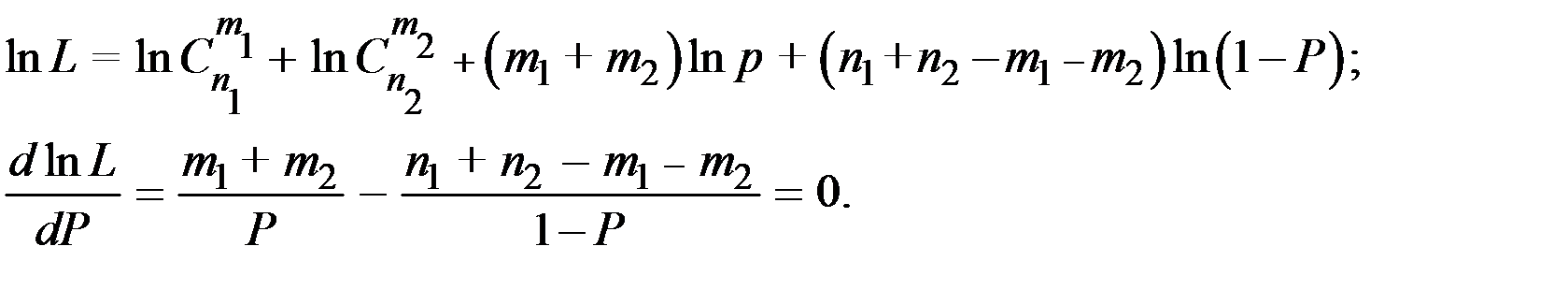
Отсюда .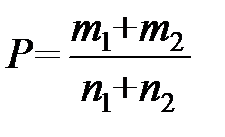

4. Метод наименьших квадратов.

Согласно этому методу наилучшим приближением оценок будут такие, которые обращают в минимум функционал

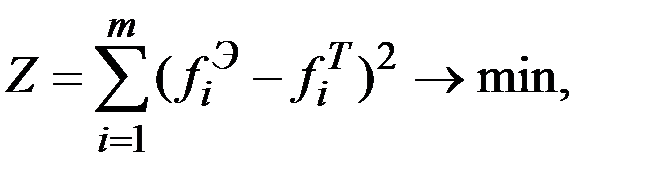
где 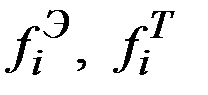 – соответственно статистические (эмпирические) и теоретические значения закона распределения для i–го интервала (для i–го значения дискретной СВ).

Приравнивая к нулю частные производные функционала Z по каждому неизвестному параметру, получают систему уравнений (по числу неизвестных параметров закона распределения случайной величины), из которой определяют требуемые параметры.

Обычно такие вычисления производятся с использованием ЭВМ.