Для точного нахождения доверительных интервалов необходимо знать заранее вид закона распределения СВ Х, тогда как для приближённых методов это не обязательно.

Идея точных методов нахождения доверительных интервалов сводится к следующему.

Любой доверительный интервал находится из условия, выражающего вероятность выполнения некоторых неравенств, в которые входит интересующая нас оценка.

Закон распределения оценки в общем случае зависит от самих неизвестных параметров СВ Х. Однако иногда удаётся перейти в неравенствах от случайной величины 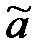 к какой–либо другой функции имеющихся значений 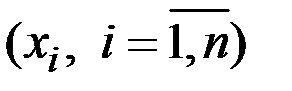, закон которой зависит только от числа опытов n и от вида закона распределения СВ Х.

Такого рода СВ играют большую роль в математической статистике.

Наиболее подробно они изучены для некоторых параметров нормального распределения случайной величины Х.

Например, доказано, при нормальном распределении случайной величины Х величина 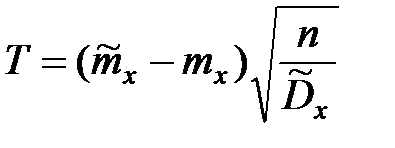 подчиняется закону Т – распределения Стьюдента с (n – 1) степенями свободы.

Доказано также, что при нормальном распределении СВ Х величина 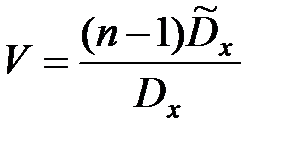 подчиняется закону c ²– распределения с (n – 1) степенями свободы.

Покажем, как можно использовать эти особенности при построении доверительных интервалов для математического ожидания 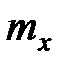 и дисперсии .

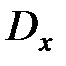Выберем e так, чтобы выполнялось условие для математического ожидания

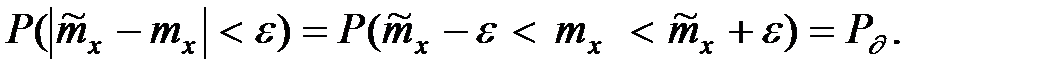
Перейдём в левой части этого соотношения от случайной величины 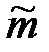 к величине Т, подчиняющейся закону Стьюдента.

Для этого умножим обе части неравенства 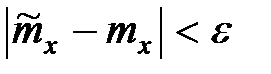 на положительную величину .

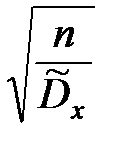Получим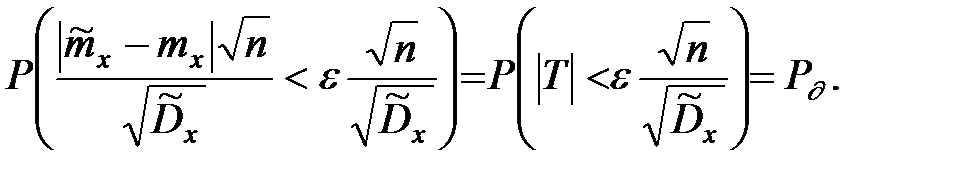      

С учётом чётности распределения Стьюдента и обозначения

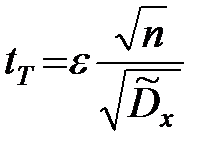
можно заключить, что  

.

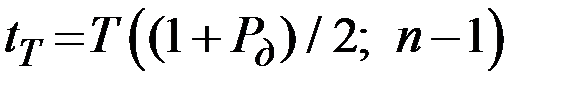Параметр 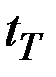 определяется по таблице квантилей Т–распределения Стьюдента.

Окончательно для математического ожидания 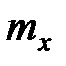 получаем доверительные границы (доверительный интервал):    

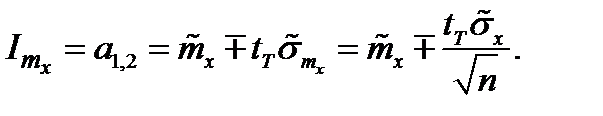
Получим доверительные границы для дисперсии.

Выразим величину 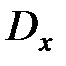 через величину

.

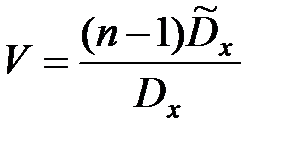Зная закон распределения величины V (c ² – распределение с (n–1) степенями свободы), можно найти интервал I_v, в который она попадает с вероятностью Р_д.

В силу несимметричности закона c ² – распределения выбирают интервал I_v так, чтобы вероятности выхода величины V за пределы доверительного интервала вправо и влево были одинаковы и равны (1 – Р_д)/2.

Доверительные границы такого интервала можно определить с помощью таблиц квантилей c ² – распределения:

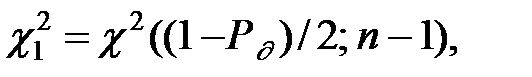
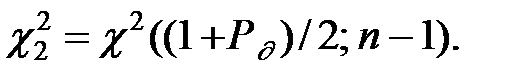
Имеем соотношения

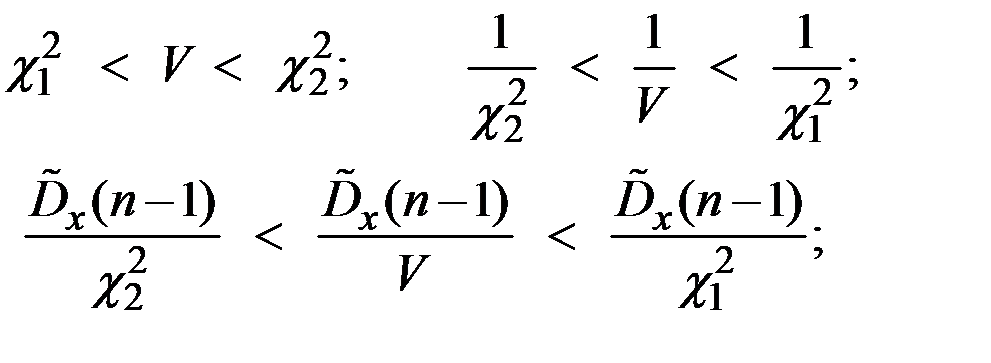
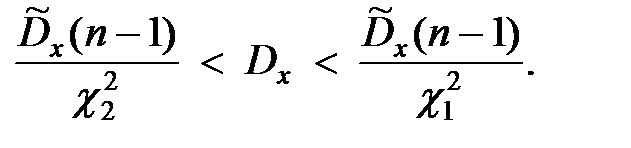
Окончательно получаем доверительные границы для дисперсии :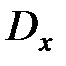

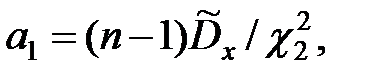
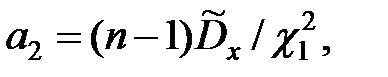
где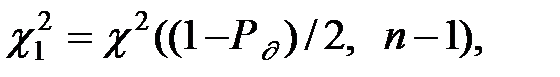                                         

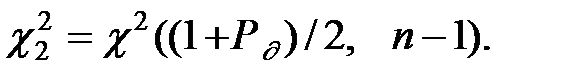
Пример 1.6. Провели 20 замеров диаметров изготавливаемых штамповкой втулок. Получили следующие значения (в мм): 10,85; 10,41; 11,05; 10,52; 10,43; 11,02; 10,56; 10,73; 10,85; 10,94; 11,00; 10,52; 10,55; 10,79; 11,04; 11,07; 10,84; 10,77; 10,65; 10,92. Требуется найти точечные оценки для математического ожидания и среднего квадратичного отклонения величины X и построить для них доверительные интервалы, соответствующие доверительной вероятности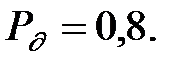

Решение.

1. Вычислим точечные оценки требующихся параметров

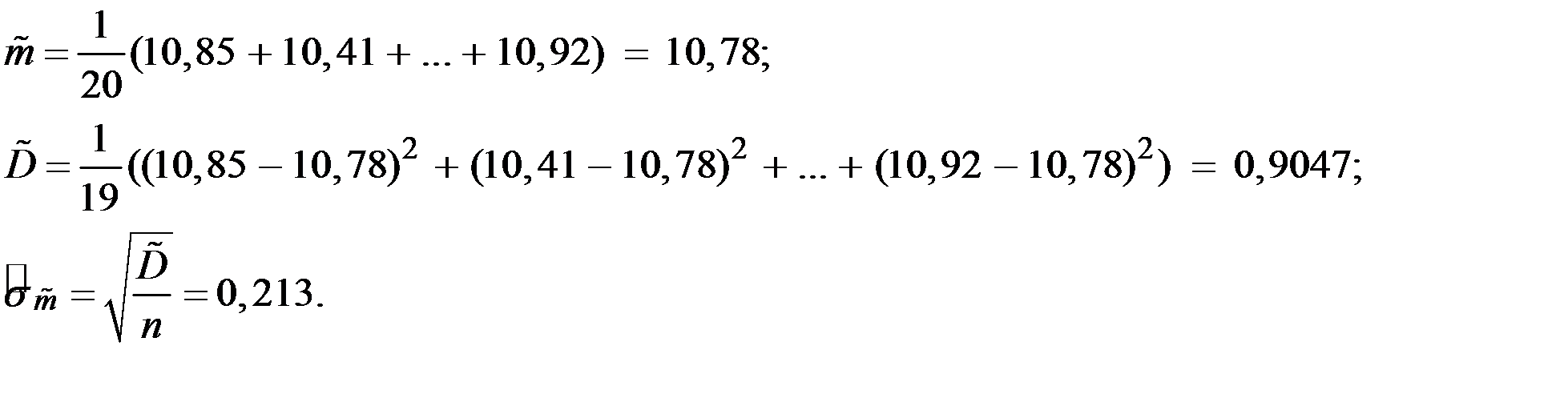
2. По таблице функции Лапласа для 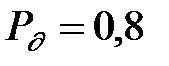 находим 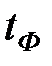= 1,282.

Тогда            

.

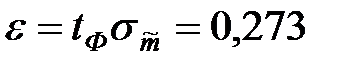Доверительные границы для математического ожидания:

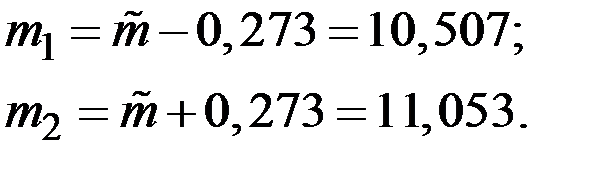
Доверительный интервал для математического ожидания:

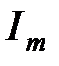= (10,507; 11,053).

3. Найдём приближённо 80% – й доверительный интервал для дисперсии, считая, что величина X распределена по нормальному закону.

Имеем:

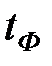= 1,282.

.

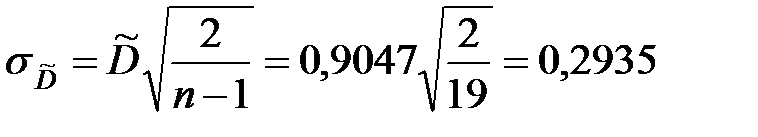Тогда доверительный интервал для дисперсии будет равен

.

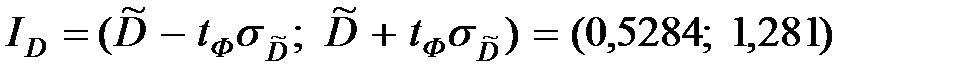Граница интервала для среднего квадратического отклонения получаются как квадратные корни из соответствующих границ доверительного интервала для дисперсии:

 = (0,727; 1,132).

4. Найдём точный доверительный интервал для математического ожидания, считая X нормальной величиной.

Имеем

n = n – 1 = 19;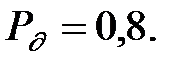

По таблице квантилей Т–распределения Стьюдента при n = 19, 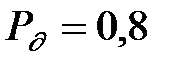 находим  

.

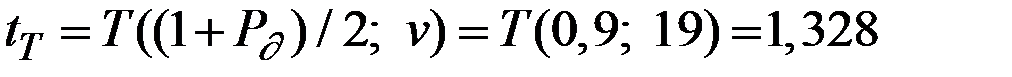Отсюда предельная ошибка выборки (точность) для математического ожидания составит величину      

.

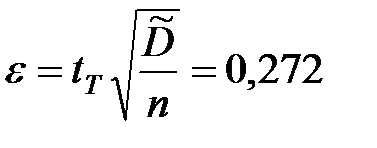Доверительный интервал для математического ожидания:

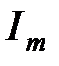= (10,508; 11,052).

Расхождение точного и приближённого доверительных интервалов незначительное.

Если сохранить точность до второго знака после запятой, то доверительные интервалы, найденные точным и приближённым методами, совпадают:             

 = (10,51; 11,05).

5. Найдём точный доверительный интервал для дисперсии, считая X нормальной величиной.

Имеем           

.

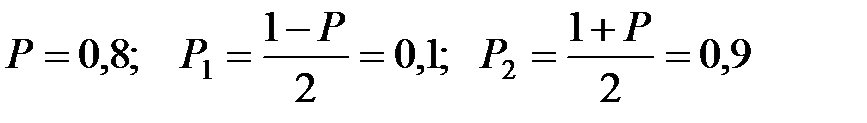Для 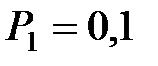 и 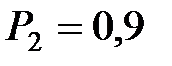 при n = n – 1 = 19 по таблице квантилей хи–квадрат распределения находим, соответственно:

;    

.

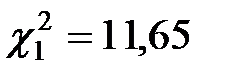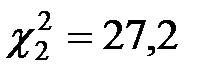Тогда              

.

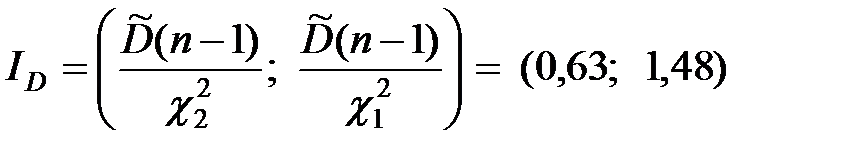6. Соответствующий доверительный интервал для среднего квадратического отклонения:      

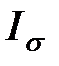 = (0,794; 1,217).