1. При некоторых условиях перевозки груза из определённого пункта отправления Ai в пункт назначения Bj не могут быть осуществлены.
Для определения оптимальных планов таких задач предполагают, что тариф перевозки единицы груза из пункта Ai в пункт В j является сколь угодно большой величиной М, и при этом условии известными методами находят решение новой транспортной задачи. При таком предположении исключается возможность (при оптимальном плане транспортной задачи) перевозить груз из пункта Ai в пункт В j.
Такой подход называют запрещением перевозок или блокированием соответствующей клетки таблицы данных транспортной задачи.
2. В отдельных транспортных задачах дополнительным условием является обеспечение перевозки по соответствующим маршрутам определённого количества груза.
Пусть, например, из пункта отправления Ai в пункт назначения В j требуется обязательно перевести dij единиц груза. Тогда в клетку таблицы данных транспортной задачи, находящуюся на пересечении строки Ai и столбца В j, записывает указанное число a ij и в дальнейшем эту клетку считают свободной со сколь угодно большим тарифом перевозок М.
Для полученной новой транспортной задачи находят оптимальный план, который определяет оптимальный план исходной задачи.
3. Иногда требуется найти решение транспортной задачи, при котором из пункта отправления Ai в пункт назначения В j должно быть завезено не менее заданного количества груза a ij. Для определения оптимального плана такой задачи считают, что запасы пункта Ai и потребности пункта В j меньше фактических на a ij единиц.
После этого находят оптимальный план новой транспортной задачи, на основании которого и определяют решение исходной задачи.
4. В некоторых транспортных задачах требуется найти оптимальный план перевозок при условии, что из пункта отправления Ai в пункт назначения В j перевозится не более чем a ij единиц груза, т.е.
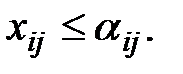(7.13)
Сформулированную задачу можно решить так.
В таблице исходных данных задачи для каждого j–го ограничения (7.13) предусматривают дополнительный столбец, т.е. вводят дополнительный пункт назначения. В данном столбце записывают те же тарифы, что и в столбце В j, за исключением тарифа, находящегося в i–й строке.
В дополнительном столбце в этой строке тариф считают равным некоторому сколь угодно большому числу М.
При этом потребности пункта В j считают равными a i j, а потребности вновь введённого пункта назначения полагают равными bj – a ij.
Решение полученной транспортной задачи может быть найдено методом потенциалов, и тем самым будет определён оптимальный план или установлена неразрешимость исходной задачи.
Заметим, что исходная транспортная задача разрешима лишь в том случае, когда для неё существует хотя бы один опорный план.
Если в результате составления плана поставок все имеющиеся запасы пунктов отправления распределены и потребности в пунктах назначения удовлетворены, то получен опорный план транспортной задачи.
Если в какой–то строке (а следовательно, и в столбце) остался нераспределённый остаток, равный d, то вводят дополнительный пункт назначения и дополнительный пункт отправления с потребностями и запасами, равными d. В клетке, находящейся на пересечении столбца дополнительного пункта назначения и строки дополнительного пункта отправления, тариф считают равным нулю.
Во всех остальных клетках данной строки и столбца тарифы полагают равными некоторому сколь угодно большому числу М. Полученную в результате этого транспортную задачу решают методом потенциалов.
После конечного числа шагов либо устанавливают, что исходная задача не имеет опорного плана, либо находят её оптимальный план.
При этом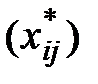 
– оптимальный план исходной задачи, если
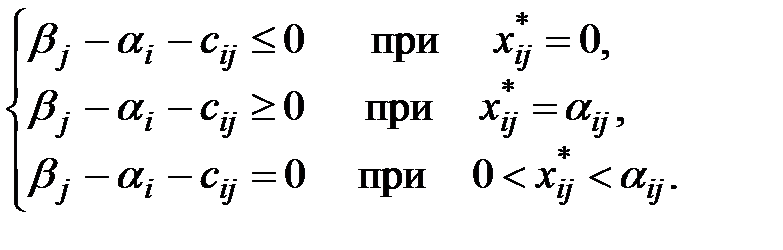
КОНТРОЛЬНЫЕ ВОПРОСЫ ПО ТЕМЕ 7
1. Поясните классы моделей математического программирования.
2. Какие приёмы используются для приведения задачи линейного программирования к каноническому виду?
3. Каким образом задача максимизации может быть сведена к задаче минимизации и наоборот?
4. Охарактеризуйте особенности решения транспортной задачи.
5. Укажите пути нахождения оптимального плана транспортных задач, имеющих некоторые усложнения в их постановке.
8. Поясните механизм использования метода северо–западного угла.
9. Поясните методику использования метода потенциалов.
Задание 7.1. Объём производства определяется производственной функцией Кобба–Дугласа в виде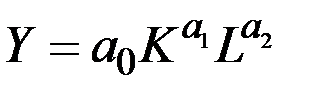 
, стоимость единицы капитальных 
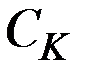и трудовых ресурсов 
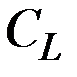известны (см. табл. исходных данных, все величины измеряются в условных единицах). Производство имеет ресурсное ограничение 
.
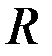Определить оптимальное распределение ресурсов, обеспечивающее максимальный выпуск продукции.
Определить параметр (множитель) Лагранжа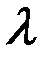 
.
Дать физическую интерпретацию всех величин.
Исходные данные
| № варианта | Параметры модели | Ресурсное ограничение | Стоимость единицы капитала | Стоимость единицы труда | ||
| 
| 
| ||||
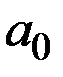
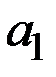
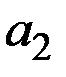
| 1 | 3,7 | 0,24 | 0,89 | 947 | 3,3 | 2,4 |
| 2 | 12,8 | 0,39 | 0,81 | 6500 | 5,2 | 3,1 |
| 3 | 4,7 | 0,17 | 0,52 | 1000 | 5,3 | 2,4 |
| 4 | 5,8 | 0,35 | 0,71 | 1653 | 8,4 | 5,0 |
| 5 | 0,7 | 0,29 | 0,66 | 2407 | 3,7 | 4,7 |
| 6 | 7,8 | 0,39 | 0,81 | 985 | 2,8 | 5,8 |
| 7 | 0,8 | 0,17 | 0,82 | 3349 | 4,7 | 3,7 |
| 8 | 5,8 | 0,35 | 0,71 | 883 | 5,0 | 2,8 |
| 9 | 13,7 | 0,24 | 0,69 | 1247 | 3,1 | 4,7 |
| 10 | 2,8 | 0,55 | 0,85 | 653 | 2,8 | 5,8 |
| 11 | 0,7 | 0,31 | 0,81 | 1349 | 4,4 | 6,7 |
| 12 | 5,8 | 0,42 | 0,82 | 6530 | 2,2 | 3,8 |
| 13 | 9,7 | 0,31 | 0,71 | 2247 | 4,7 | 7,7 |
| 14 | 2,8 | 1,24 | 0,12 | 320 | 9,4 | 15,8 |
| 15 | 4,7 | 0,39 | 0,85 | 1653 | 5,1 | 3,3 |
| 16 | 5,8 | 0,27 | 0,80 | 2350 | 4,9 | 5,6 |
| 17 | 3,7 | 0,35 | 0,82 | 6500 | 5,8 | 1,3 |
| 18 | 8,8 | 0,24 | 0,71 | 2400 | 3,7 | 8,4 |
| 19 | 0,7 | 0,34 | 0,85 | 2653 | 2,8 | 3,7 |
| 20 | 5,8 | 0,27 | 0,81 | 3049 | 4,3 | 3,8 |
| 21 | 3,7 | 0,35 | 0,82 | 4500 | 5,8 | 4,7 |
| 22 | 7,8 | 0,54 | 0,71 | 870 | 3,7 | 5,1 |
| 23 | 4,7 | 0,24 | 0,86 | 2400 | 6,4 | 3,0 |
| 24 | 6,5 | 0,39 | 0,77 | 6500 | 5,1 | 5,2 |
| 25 | 4,4 | 0,19 | 0,76 | 1560 | 3,1 | 5,8 |
Задание 7.2. Четыре предприятия данного экономического района для производства продукции используют три вида сырья. Известны потребности в сырье каждого из предприятий. Сырьё сосредоточено в трёх местах его получения, запасы которых известны. На каждое из предприятий сырьё может завозиться из любого пункта его получения. Тарифы перевозок являются известными величинами и задаются соответствующей матрицей (см. варианты задания). Составить план перевозок, при котором общая стоимость перевозок является минимальной.
Вариант 1.
| Пункты отправления | Пункты назначения | Запасы | |||
| B1 | B2 | B3 | B4 | ||
| A1 A2 A3 | 7 4 3 | 4 2 8 | 17 12 18 | 5 8 2 | 120 280 160 |
| Потребности | 130 | 220 | 60 | 70 | |
Вариант 2.
| Пункты отправления | Пункты назначения | Запасы | |||
| B1 | B2 | B3 | B4 | ||
| A1 A2 A3 | 4 6 3 | 8 2 11 | 4 6 5 | 5 8 12 | 420 230 560 |
| Потребности | 230 | 320 | 160 | 170 | |
Вариант 3.
| Пункты отправления | Пункты назначения | Запасы | |||
| B1 | B2 | B3 | B4 | ||
| A1 A2 A3 | 8 12 11 | 57 62 68 | 35 34 33 | 27 32 11 | 200 280 320 |
| Потребности | 300 | 220 | 130 | 200 | |
Вариант 4.
| Пункты отправления | Пункты назначения | Запасы | |||
| B1 | B2 | B3 | B4 | ||
| A1 A2 A3 | 24 36 43 | 8 22 11 | 34 16 25 | 5 8 12 | 520 300 600 |
| Потребности | 200 | 320 | 400 | 170 | |
Вариант 5.
| Пункты отправления | Пункты назначения | Запасы | |||
| B1 | B2 | B3 | B4 | ||
| A1 A2 A3 | 2 5 7 | 4 6 2 | 7 8 4 | 3 9 8 | 510 90 120 |
| Потребности | 270 | 140 | 200 | 110 | |
Вариант 6.
| Пункты отправления | Пункты назначения | Запасы | |||
| B1 | B2 | B3 | B4 | ||
| A1 A2 A3 | 4 6 3 | 8 22 11 | 4 6 5 | 15 17 12 | 420 400 560 |
| Потребности | 230 | 350 | 160 | 270 | |
Вариант 7.
| Пункты отправления | Пункты назначения | Запасы | |||
| B1 | B2 | B3 | B4 | ||
| A1 A2 A3 | 8 12 11 | 14 16 13 | 17 12 18 | 27 32 11 | 220 280 320 |
| Потребности | 300 | 180 | 130 | 200 | |
Вариант 8.
| Пункты отправления | Пункты назначения | Запасы | |||
| B1 | B2 | B3 | B4 | ||
| A1 A2 A3 | 6 5 11 | 4 1 6 | 7 8 4 | 9 12 3 | 200 270 130 |
| Потребности | 120 | 80 | 240 | 160 | |
Вариант 9.
| Пункты отправления | Пункты назначения | Запасы | |||
| B1 | B2 | B3 | B4 | ||
| A1 A2 A3 | 31 34 43 | 7 2 8 | 29 26 17 | 5 8 2 | 120 280 160 |
| Потребности | 130 | 220 | 60 | 70 | |
Вариант 10.
| Пункты отправления | Пункты назначения | Запасы | |||
| B1 | B2 | B3 | B4 | ||
| A1 A2 A3 | 14 16 13 | 8 2 11 | 17 12 18 | 35 38 12 | 420 230 560 |
| Потребности | 230 | 320 | 160 | 170 | |
Вариант 11.
| Пункты отправления | Пункты назначения | Запасы | |||
| B1 | B2 | B3 | B4 | ||
| A1 A2 A3 | 12 5 7 | 4 16 2 | 7 8 14 | 13 9 18 | 510 90 120 |
| Потребности | 270 | 140 | 200 | 110 | 720 |
Вариант 12.
| Пункты отправления | Пункты назначения | Запасы | |||
| B1 | B2 | B3 | B4 | ||
| A1 A2 A3 | 14 6 13 | 8 22 15 | 34 16 25 | 15 18 12 | 500 400 550 |
| Потребности | 200 | 390 | 400 | 170 | |
Вариант 13.
| Пункты отправления | Пункты назначения | Запасы | |||
| B1 | B2 | B3 | B4 | ||
| A1 A2 A3 | 14 16 13 | 7 2 8 | 9 6 21 | 5 8 12 | 180 280 460 |
| Потребности | 180 | 420 | 60 | 70 | |
Вариант 14.
| Пункты отправления | Пункты назначения | Запасы | |||
| B1 | B2 | B3 | B4 | ||
| A1 A2 A3 | 4 6 3 | 8 22 11 | 4 11 5 | 7 4 3 | 520 400 560 |
| Потребности | 230 | 350 | 160 | 270 | |
Вариант 15.
| Пункты отправления | Пункты назначения | Запасы | |||
| B1 | B2 | B3 | B4 | ||
| A1 A2 A3 | 8 2 11 | 14 6 13 | 5 14 3 | 7 32 11 | 120 280 320 |
| Потребности | 200 | 280 | 130 | 200 | |
Вариант 16.
| Пункты отправления | Пункты назначения | Запасы | |||
| B1 | B2 | B3 | B4 | ||
| A1 A2 A3 | 14 11 13 | 8 6 11 | 7 4 3 | 5 8 12 | 520 300 600 |
| Потребности | 180 | 320 | 400 | 170 | |
Вариант 17.
| Пункты отправления | Пункты назначения | Запасы | |||
| B1 | B2 | B3 | B4 | ||
| A1 A2 A3 | 7 4 3 | 4 2 8 | 9 6 5 | 5 8 2 | 120 280 160 |
| Потребности | 130 | 220 | 60 | 70 | |
Вариант 18.
| Пункты отправления | Пункты назначения | Запасы | |||
| B1 | B2 | B3 | B4 | ||
| A1 A2 A3 | 8 7 10 | 8 2 11 | 4 6 5 | 5 8 12 | 420 230 560 |
| Потребности | 230 | 320 | 160 | 170 | |
Вариант 19.
| Пункты отправления | Пункты назначения | Запасы | |||
| B1 | B2 | B3 | B4 | ||
| A1 A2 A3 | 8 12 11 | 57 62 68 | 35 34 33 | 27 32 20 | 400 280 320 |
| Потребности | 300 | 220 | 130 | 200 | |
Вариант 20.
| Пункты отправления | Пункты назначения | Запасы | |||
| B1 | B2 | B3 | B4 | ||
| A1 A2 A3 | 27 32 20 | 14 16 13 | 34 16 25 | 5 8 12 | 520 300 600 |
| Потребности | 200 | 320 | 400 | 170 | |
Вариант 21.
| Пункты отправления | Пункты назначения | Запасы | |||
| B1 | B2 | B3 | B4 | ||
| A1 A2 A3 | 4 6 3 | 8 22 11 | 4 11 5 | 7 4 3 | 490 410 560 |
| Потребности | 250 | 340 | 160 | 270 | |
Вариант 22.
| Пункты отправления | Пункты назначения | Запасы | |||
| B1 | B2 | B3 | B4 | ||
| A1 A2 A3 | 8 2 11 | 14 6 13 | 5 14 3 | 7 32 11 | 220 380 420 |
| Потребности | 270 | 290 | 230 | 200 | |
Вариант 23.
| Пункты отправления | Пункты назначения | Запасы | |||
| B1 | B2 | B3 | B4 | ||
| A1 A2 A3 | 14 11 13 | 8 6 11 | 7 4 3 | 5 8 12 | 330 350 580 |
| Потребности | 280 | 320 | 370 | 190 | |
ИГРОВЫЕ МОДЕЛИ В ЭКОНОМИКЕ
Основные понятия и классификация игр
В теории игр исследуются математические модели, интересы участников которых различны, причём игроки (участники) достигают своей цели различными путями. Столкновения противоположных интересов участников приводит к возникновению конфликтных ситуаций.
Задачей теории игр и является выработка рекомендаций по рациональному поведению действия участников конфликта.
Сложные конфликтные ситуации возникают, если имеются объединения или коалиции лиц, участвующих в столкновении интересов, например, в том случае, когда ставки заработной платы определяются союзами или объединениями рабочих и предпринимателей, при анализе результатов голосования в парламенте и т.п.
Конфликт может возникнуть также из различия целей, которые отражают не только несовпадающие интересы различных сторон, но и многосторонние интересы одного и того же лица. Например, разработчик экономической политики обычно преследует разнообразные цели, согласуя противоречивые требования, предъявляемые к ситуации (рост объёмов производства, повышение доходов, снижение экологической нагрузки и т.п.). Конфликт может проявляться не только в результате сознательных действий различных участников, но и как результат действия тех или иных "стихийных сил" (случай так называемых "игр с Природой").
В теории игр предполагается, что функции выигрыша и множество стратегий, доступных каждому из игроков, общеизвестны, т.е. каждый игрок знает свою функцию выигрыша и набор имеющихся в его распоряжении стратегий, а также функции выигрыша и стратегии всех остальных игроков, и в соответствии с этой информацией организует своё поведение.
Формализация содержательного описания конфликта представляет собой его математическую модель, которую называют игрой.
Различные виды игр можно классифицировать: 1) по числу игроков, 2) по числу стратегий, 3) по свойствам функций выигрыша, 4) по возможности предварительных переговоров и взаимодействия между игроками в ходе игры, 5) по источникам неопределённости результата, 5) по количеству этапов принятия решений ЛПР.
1. В зависимости от числа игроков различают игры с двумя, тремя и более участниками (табл. 8.1). Задачи теории оптимизации можно рассматривать как теорию игр с одним игроком.
Возможны также игры с бесконечным числом игроков.
2. По количеству стратегий различают конечные и бесконечные игры. В конечных играх игроки располагают конечным числом возможных стратегий. Соответственно, в бесконечных играх игроки имеют бесконечное число возможных стратегий. Так, в ситуации «Продавец–Покупатель» каждый из игроков может назвать любую устраивающую его цену и количество продаваемого (покупаемого) товара.
Таблица 8.1
Классификация игр
| № | Критерий классификации | Разновидности игр |
| 1. | Число игроков | Игры с одним (задачи оптимизации), двумя, тремя и более участниками |
| 2. | Число стратегий | 1) конечные; 2) бесконечные |
| 3. | Свойства функции выигрыша | 1) антогонистические (с нулевой суммой); 2) игры с постоянной разностью выигрыша; 3) игры с ненулевой суммой |
| 4. | Возможности переговоров и взаимодействия игроков | 1) кооперативные; 2) некооперативные |
| 5. | Источники неопределённости результата | 1) комбинаторные (многовариантные: шахматы, карты и др.); 2) азартные (случайные факторы: рулетка, кости); 3) стратегические (нет информации о действиях противника); 4) статистические (с частичной неопределённостью, игры с «Природой») |
| 6. | Количество этапов принятия решений | 1) одношаговые; 2) позиционные (многоэтапные) |
3. По свойствам функций выигрыша (платёжных функций) различают игры с нулевой суммой (антагонистические игры) и игры с постоянной разностью, в которых игроки и выигрывают, и проигрывают одновременно (так что им выгодно действовать сообща).
В антагонистических играх выигрыш одного из игроков равен проигрышу другого, т.е. налицо прямой конфликт между игроками.
Между этими двумя крайними случаями имеется множество игр с ненулевой суммой, где имеются и конфликты, и согласованные действия игроков.
По виду функции выигрышей игры можно разделить на матричные, биматричные, непрерывные, сепарабельные и т.д.
Матричными играми называются конечные игры двух игроков с нулевой суммой.
Биматричная игра – это конечная игра двух игроков с ненулевой суммой. Здесь для каждой игровой ситуации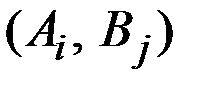 
каждый из игроков имеет свой выигрыш 
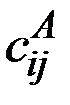для первого игрока и 
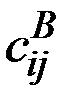– для второго игрока.
К биматричной игре сводится, например, поведение производителей на рынках несовершенной конкуренции (дуополия).
4. В зависимости от возможности предварительных переговоров между игроками различают кооперативные и некооперативные игры.
Игра называется кооперативной, если до начала игры игроки образуют коалиции и принимают взаимообязывающие соглашения о своих стратегиях. Игра, в которой игроки не могут координировать свои стратегии подобным образом, называется некооперативной. Очевидно, что все антагонистические игры могут служить примером некооперативных игр.
Примером кооперативной игры может служить ситуация образования коалиций в парламенте для принятия путём голосования решения, так или иначе затрагивающего интересы участников голосования.
5. Неопределённость результата игры вызывается различными причинами, которые можно разбить на четыре основные группы.
1). Особенности правил игры вызывают такое разнообразие в её развитии, что предсказать результат игры заранее невозможно. Источники неопределённости такого вида (как и сами игры) называются комбинаторными (шахматы, карты и др.). Однако комбинаторная сложность игр носит исторически преходящий характер благодаря использованию соответствующего математического аппарата и вычислительной техники. Для целого ряда комбинаторных игр найдены выигрышные комбинации путём решения логических задач ограниченного объёма.
2). Игры, в которых исход оказывается неопределённым исключительно в результате случайных причин, называются азартными (игры в кости, рулетка).
3). При отсутствии информации о действиях противника, о его стратегии игры называются стратегическими. Стратегические игры – это игры в условиях полной неопределённости.
4). Статистические игры характеризуются частичной неопределённостью (игры с «Природой»). В статистической игре всегда имеется один активный игрок, имеющий свои стратегии и цели. Другим игроком (пассивным, не преследующим своих целей) является «Природа». Этот игрок реализует свои стратегии (состояния природы) случайным образом, причём вероятность реализации того или иного состояния можно оценить с помощью статистического эксперимента.
6. По количеству этапов принятия решений ЛПР различают 1) одношаговые; и 2) позиционные (многоэтапные) игры.
Дата: 2019-03-05, просмотров: 339.
