Математическое программирование занимается изучением экстремальных задач и разработкой методов их решения.
В общем виде математическая постановка экстремальной задачи состоит в определении наибольшего или наименьшего значения целевой функции
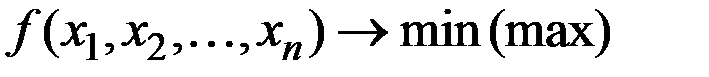
при условиях
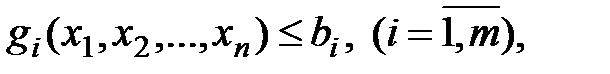
где 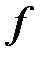 и
и 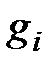 – заданные функции, а
– заданные функции, а 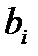 – некоторые действительные числа.
– некоторые действительные числа.
В зависимости от свойств функций 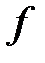 и
и 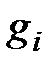 можно рассматривать ряд самостоятельных дисциплин, занимающихся изучением и разработкой методов решения определённых классов задач.
можно рассматривать ряд самостоятельных дисциплин, занимающихся изучением и разработкой методов решения определённых классов задач.
Прежде всего, задачи математического программирования делятся на задачи линейного и нелинейного программирования.
При этом если все функции 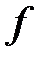 и
и 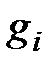 линейные, то соответствующая задача является задачей линейного программирования.
линейные, то соответствующая задача является задачей линейного программирования.
Если же хотя бы одна из указанных функций нелинейная, то соответствующая задача является задачей нелинейного программирования.
Наиболее изученным разделом математического программирования является линейное программирование. Для решения задач линейного программирования разработан целый ряд эффективных методов (например, симплексный метод), алгоритмов и программ.
Среди задач нелинейного программирования наиболее глубоко изучены задачи выпуклого программирования. Это задачи, в результате решения которых определяется минимум выпуклой (или максимум вогнутой) функции, заданной на выпуклом замкнутом множестве.
В свою очередь, среди задач выпуклого программирования более подробно исследованы задачи квадратичного программирования.
В результате решения таких задач требуется в общем случае найти максимум (или минимум) квадратичной функции при условии, что её переменные удовлетворяют некоторой системе линейных неравенств или линейных уравнений либо некоторой системе, содержащей как линейные неравенства, так и линейные уравнения.
Отдельными классами задач математического программирования являются задачи целочисленного, параметрического и дробно–линейного программирования.
В задачах целочисленного программирования неизвестные могут принимать только целочисленные значения.
В задачах параметрического программирования целевая функция или функции, определяющие область возможных изменений переменных, либо то и другое зависят от некоторых параметров.
В задачах дробно–линейного программирования целевая функция представляет собой отношение двух линейных функций, а функции, определяющие область возможных изменений переменных, также являются линейными.
Выделяют отдельные классы задач стохастического и динамического программирования. Если в целевой функции или в функциях, определяющих область возможных изменений переменных, содержатся случайные величины, то такая задача относится к задаче стохастического программирования. Задача, процесс нахождения решения которой является многоэтапным, относится к задаче динамического программирования.
Пример 7.1. На швейной фабрике ткань может быть раскроена несколькими способами для изготовления нужных деталей швейных изделий. Пусть при j–м варианте раскроя 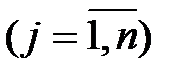 100 м2 ткани изготовляется
100 м2 ткани изготовляется 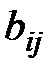 деталей i–го вида
деталей i–го вида 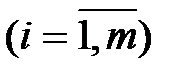 , а величина отходов при данном варианте раскроя равна cj м2. Зная, что деталей i–го вида следует изготовлять B i штук, требуется раскроить ткань так, чтобы было получено необходимое количество деталей каждого вида при минимальных общих отходах.
, а величина отходов при данном варианте раскроя равна cj м2. Зная, что деталей i–го вида следует изготовлять B i штук, требуется раскроить ткань так, чтобы было получено необходимое количество деталей каждого вида при минимальных общих отходах.
Составить математическую модель задачи.
Решение. Предположим, что по j–му варианту раскраивается x j сотен м2 ткани. Поскольку при раскрое 100 м2 ткани по j–му варианту получается b ij деталей i–го вида, по всем вариантам раскроя из используемых тканей будет получено 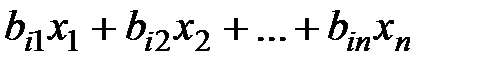 деталей j–го вида.
деталей j–го вида.
Так как должно быть изготовлено B i деталей данного вида, то
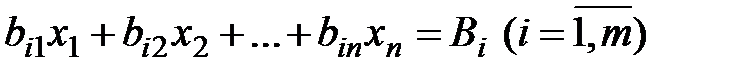 .
.
Общая величина отходов по всем вариантам раскроя ткани составит
F = с1 x 1 + с2х2 +…+ cnxn .
Таким образом, приходим к следующей математической задаче: найти минимум функции 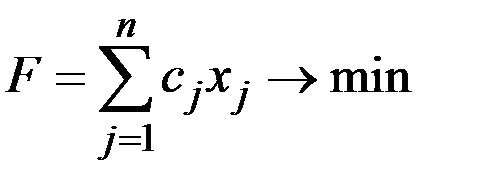
при условии, что её переменные удовлетворяют системе уравнений
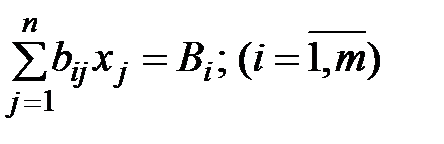
и условию неотрицательности переменных 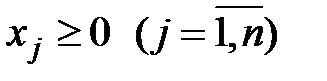 .
.
Сформулированная задача является задачей линейного программирования, так как целевая функция линейная, а система ограничений содержит только лишь линейные уравнения.
Общей задачей линейного программирования называется задача, которая состоит в определении максимального (минимального) значения функции
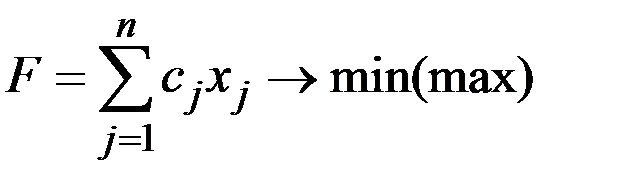 (7.1)
(7.1)
при условиях
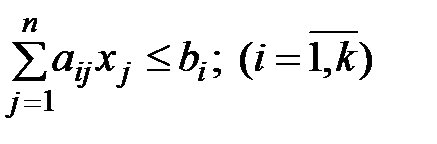 (7.2)
(7.2)
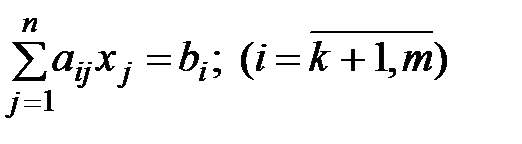 ; (7.3)
; (7.3)
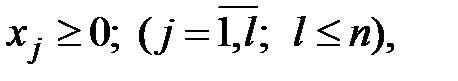 (7.4)
(7.4)
где 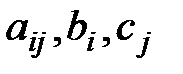 – заданные постоянные величины и
– заданные постоянные величины и 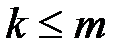 .
.
Функция (7.1) называется целевой функцией (или линейной формой) задачи (7.1) – (7.4), а условия (7.2) – (7.4) – ограничениями данной задачи.
Стандартной (или симметричной) задачей линейного программирования называется задача, которая состоит в определении максимального значения функции (7.1) при выполнении условий (7.2) и (7.4), где 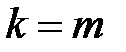 и
и 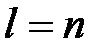 .
.
Канонической (или основной) задачей линейного программирования называется задача, которая состоит в определении максимального значения функции (7.1) при выполнении условий (7.3) и (7.4), где 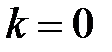 и
и 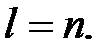
Совокупность чисел 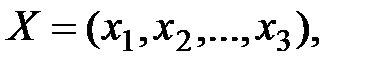 удовлетворяющих ограничениям задачи (7.2) – (7.4), называется допустимым решением (или планом).
удовлетворяющих ограничениям задачи (7.2) – (7.4), называется допустимым решением (или планом).
План X* = (x1*, x2*,…, x n*), при котором целевая функция задачи (7.1) принимает своё максимальное (минимальное) значение, называется оптимальным.
Указанные выше три формы задачи линейного программирования эквивалентны в том смысле, что каждая из них с помощью несложных преобразований может быть переписана в форме другой задачи.
Это означает, что если имеется способ нахождения решения одной из указанных задач, то тем самым может быть определён оптимальный план любой из трёх задач.
Чтобы перейти от одной формы записи задачи линейного программирования к другой, нужно уметь: 1) сводить задачу минимизации функции к задаче максимизации; 2) переходить от ограничений–неравенств к ограничениям–равенствам и наоборот; 3) заменять переменные, которые не подчинены условию неотрицательности.
Если требуется найти минимум функции 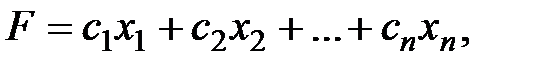 то можно перейти к нахождению максимума противоположной функции
то можно перейти к нахождению максимума противоположной функции 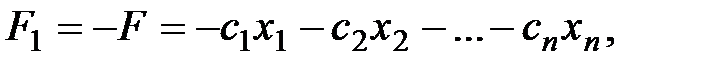 поскольку
поскольку 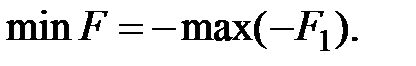
Ограничение–неравенство исходной задачи линейного программирования, имеющее вид “ £ ”, можно преобразовать в ограничение–равенство добавлением к его левой части дополнительной неотрицательной переменной, а ограничение–неравенство вида “ ³ ” – в ограничение–равенство вычитанием из его левой части дополнительной неотрицательной переменной.
Таким образом, ограничение–неравенство
a i 1 x1 + a i 2 x2 +…+ ain xn £ bi
преобразуется в ограничение–равенство
ai 1 x 1 + ai 2 x 2 +…+ ain xn + xn +1 = bi ( xn +1 ³ 0 ),
а ограничение–неравенство
a i 1 x1 + а i 2 х2 +…+ а in х n ³ bi
– в ограничение–равенство
ai 1 x 1 + ai 2 x 2 +…+ ain xn – xn +1 = bi ( xn +1 ³ 0 ) .
В то же время каждое уравнение вида
ai1 x1 + ai2x2 +…+ ain xn = bi
можно записать в виде неравенств:
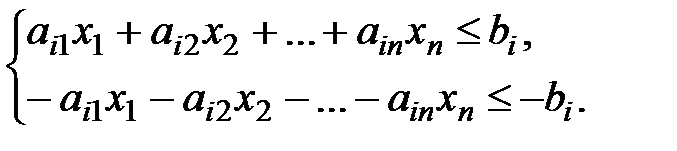
Число вводимых дополнительных неотрицательных переменных при преобразовании ограничений–неравенств в ограничения–равенства равно числу преобразуемых неравенств.
Вводимые дополнительные переменные имеют вполне определённый экономический смысл. Так, если в ограничениях исходной задачи линейного программирования отражается расход и наличие производственных ресурсов, то числовое значение дополнительной переменной в плане задачи, записанной в форме основной, равно объёму неиспользуемого соответствующего ресурса.
Отметим, наконец, что если переменная x k не подчинена условию неотрицательности, то её следует заменить двумя неотрицательными переменными u k и vk , приняв x k = u k – vk .
Дата: 2019-03-05, просмотров: 751.