В равновесии по Вальрасу совокупный спрос на каждый товар должен быть равен предложению этого товара. В экономике обмена производство отсутствует, и предложение товара равно его запасу.
Можно найти спрос каждого потребителя (участника рынка) на каждый товар из решения соответствующей задачи максимизации полезности при бюджетном ограничении. При этом доход равен запасам, умноженным на соответствующие цены.
Пример 6.4. В экономике обмена имеется два товара x и y и два потребителя, А и В, предпочтения которых представлены функциями полезности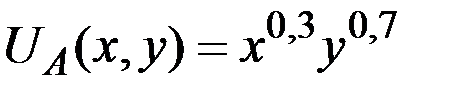 
и 
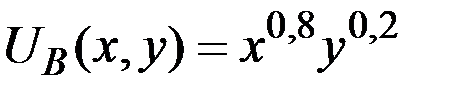, соответственно. Первоначальные запасы потребителей заданы векторам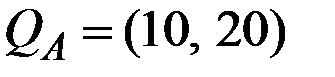и 
и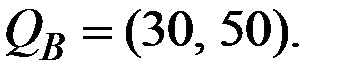 
Найдите равновесие по Вальрасу и множество Парето–оптимальных распределений благ (товаров).
Решение. Найдём спрос каждого потребителя (участника рынка) на каждый товар из решения соответствующей задачи максимизации полезности при бюджетном ограничении. При этом доход равен запасам, умноженным на соответствующие цены:
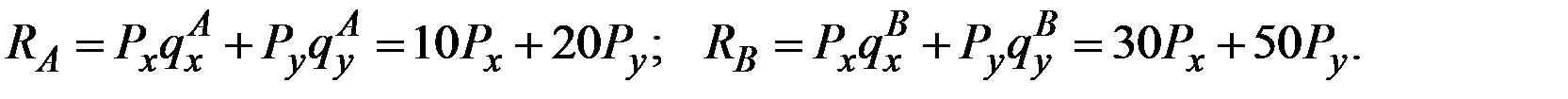
Поскольку предпочтения обоих участников представлены функциями полезности Стоуна вида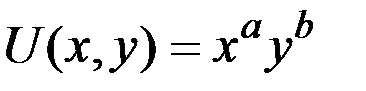 
, то расходы на каждый товар будут представлять фиксированную долю дохода участников обмена.
Соответственно, функции спроса примут вид:
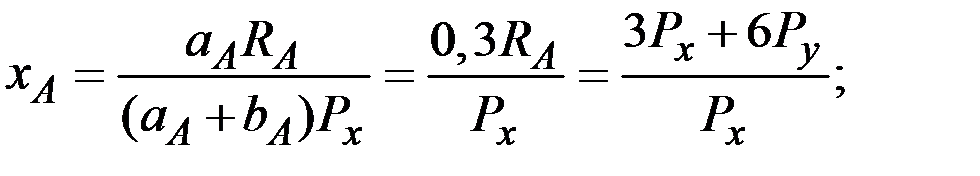
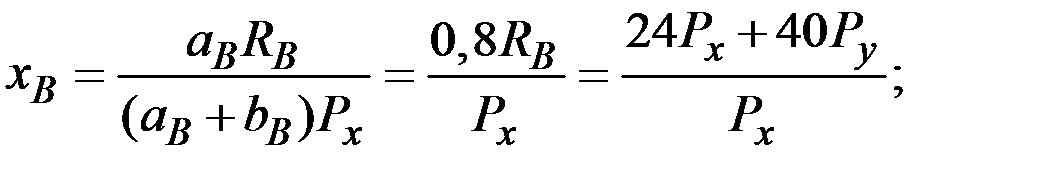
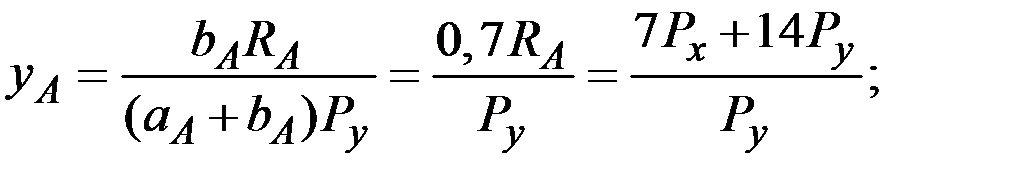
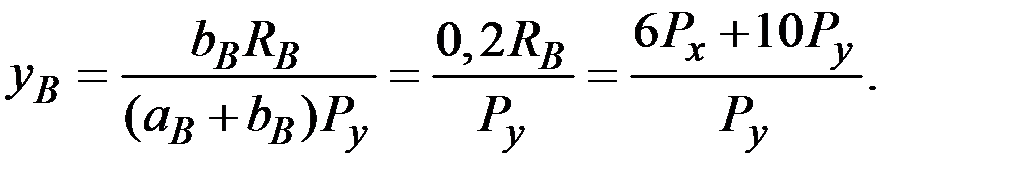
Найдём совокупный спрос на товар x и приравняем его к запасу этого товара в экономике:
Отсюда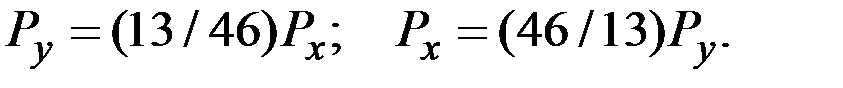 
В силу закона Вальраса эти же цены автоматически уравновесят и рынок товара у. Подставляя найденные цены в функции спроса, находим равновесное распределение
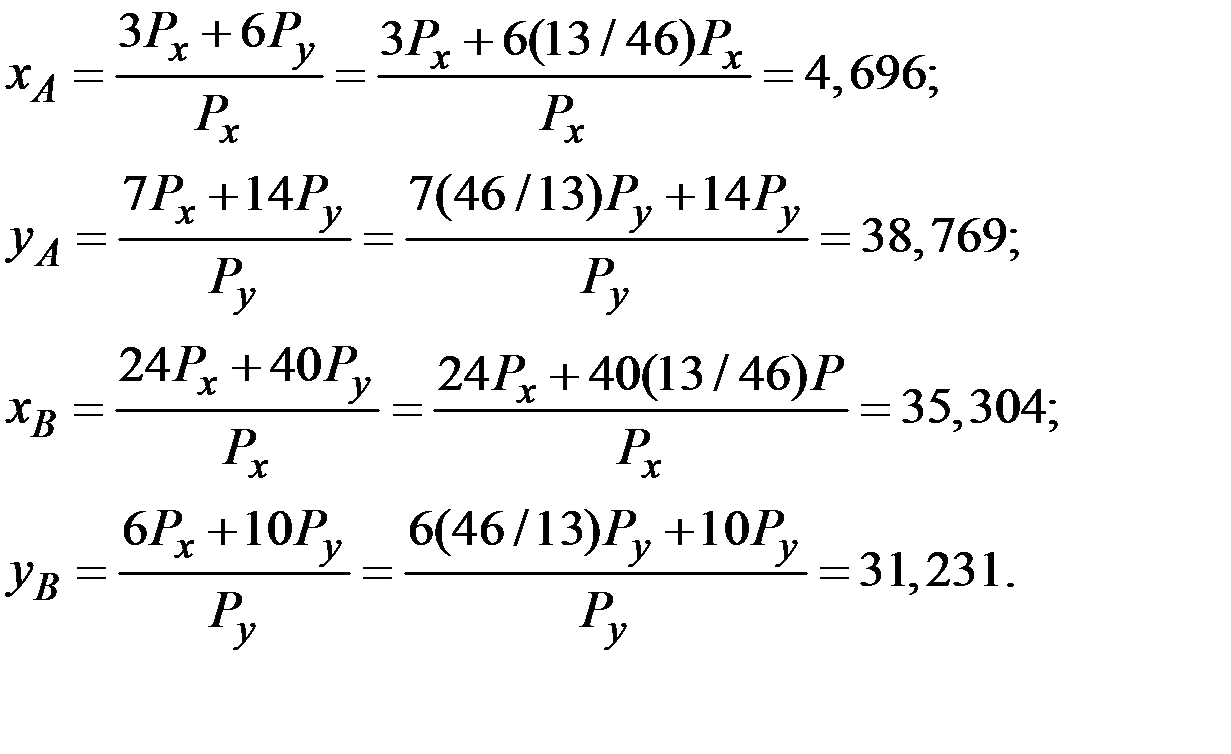
Функции полезности потребителей при равновесии будут равны: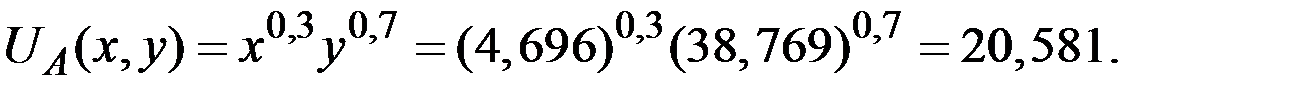 
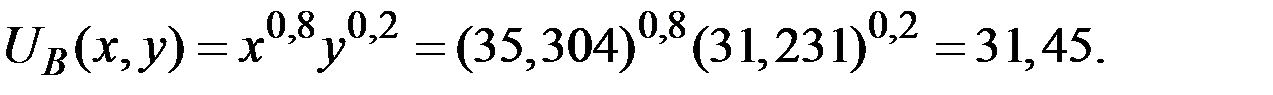
Допустимое распределение благ (товаров) называется Парето–оптимальным, если не существует другого допустимого распределения, которое для всех потребителей было бы не хуже и хотя бы для одного строго лучше.
Из условия допустимости имеем соотношения
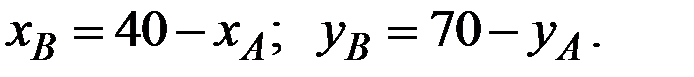
Необходимым (и достаточным при убывании предельной нормы замещения) условием принадлежности распределения (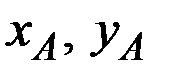 
) множеству Парето является равенство норм замещения благ потребителей:
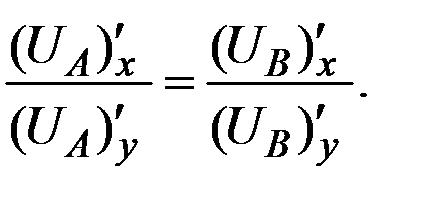
Так как
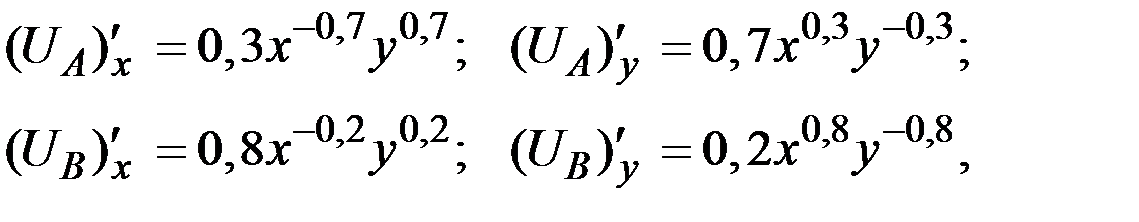
то
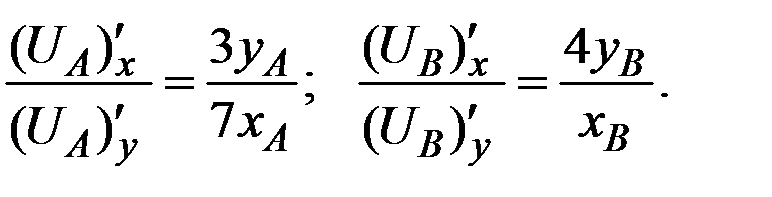
Тогда
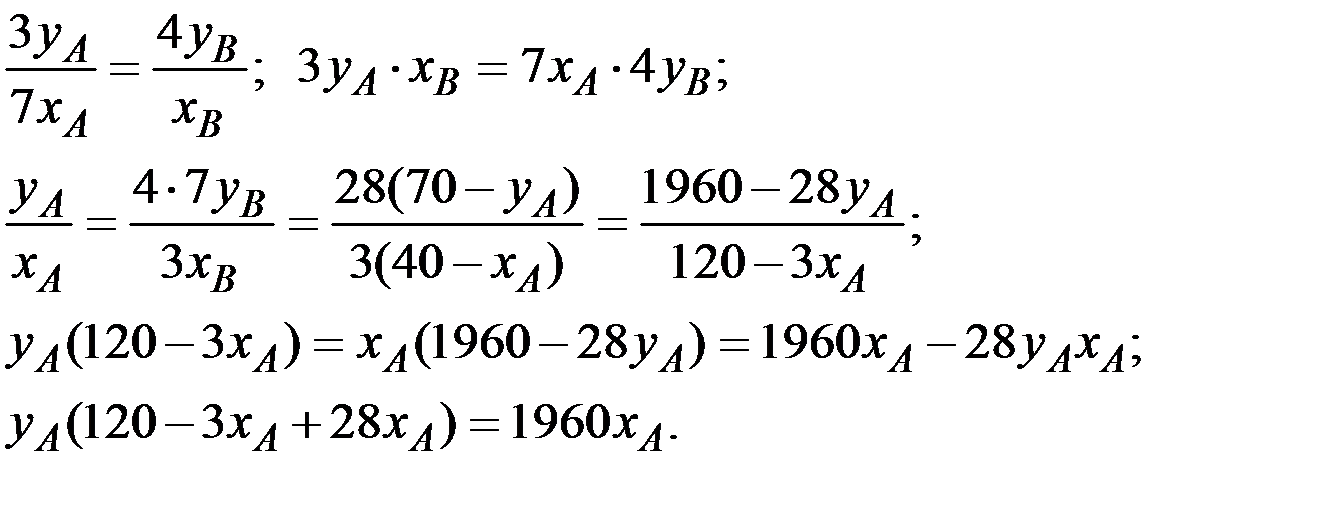
Получаем Парето–оптимальное распределение благ (товаров) для первого участника обмена:
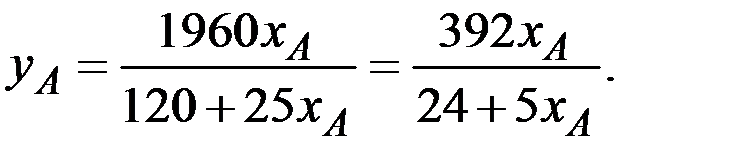
Заметим, что в данной экономике граничные распределения, где у участника отсутствует запас одного из благ, но имеется запас другого блага, не является Парето оптимальным.
Действительно, отдав имеющееся благо другому участнику, агент сохранит нулевой уровень полезности, но при этом второй агент, получив данный товар, улучшит своё благосостояние.
Из граничных распределений Парето–оптимальными будут лишь два, где запасы обоих благ принадлежат лишь одному из потребителей.
Заметим, что эти распределения удовлетворяют уравнению
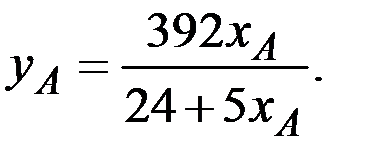
Эта формула описывает все Парето–оптимальные распределения.
В частности, для отдельных значений количества благ получаем:
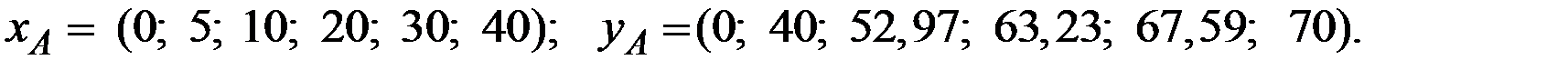
Аналогично получаем Парето–оптимальное распределение благ (товаров) для второго участника обмена:
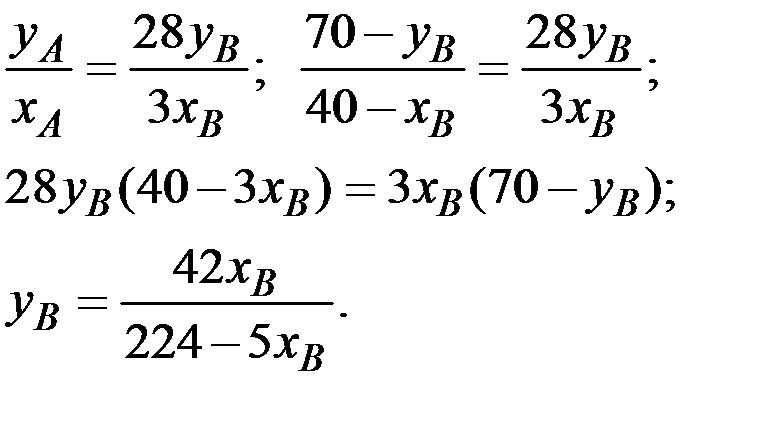
Для отдельных значений количества благ получаем Парето–оптимальное распределение благ для второго участника обмена:
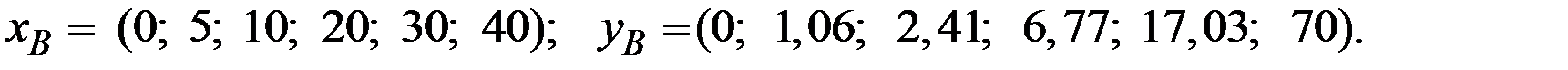
Пример 6.5. На основании данных о потреблении взаимозаменяемых и взаимодополняемых продуктов x1 и x2 в различном сочетании i, их цене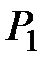 
и 
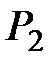, полезности U и бюджете (доходах) потребителя R построить кривую безразличия и определить оптимальный план потребления названных продуктов. Исходные данные задачи имеют вид:
| № набл. i | Продукт х1i | Продукт х2i |
| 1 | 2,9 | 13,5 |
| 2 | 3,0 | 12,0 |
| 3 | 5,0 | 7,5 |
| 4 | 7,0 | 6,0 |
| 5 | 10,0 | 5,0 |
| 6 | 12,0 | 4,5 |
| 7 | 12,3 | 4,6 |
U = 18; P1 = 5; P2 = 10,3; R = 100.
Решение. В нашей задаче продукты х1 и х2 являются взаимозаменяемыми и взаимодополняемыми, т.е. функция смешанная.
Поэтому можно воспользоваться моделью неоклассической функции полезности, которая имеет вид
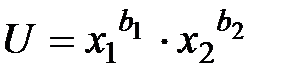, где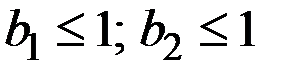 
.
Чтобы убедиться в правильности предположения о форме связи, следует графически изобразить изучаемую зависимость в системе координат по данным о потреблении продуктов х1 и х2.
По виду графика можно предположить, что зависимость между x1 и x2 имеет вид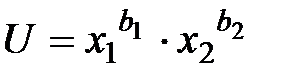 
при .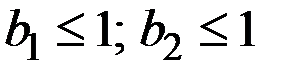
Решение задачи по построению кривой безразличия заключается в определении параметров функции b1 и b2.
Параметры кривой безразличия b1 и b2 отражают степень полезности каждого из продуктов x1 и x2.
Определив параметры b1 и b2, зная одну из переменных – количество потребления продукта x1, всегда можно определить вторую переменную x2 так, чтобы обеспечить максимум полезности от потребления продуктов
.
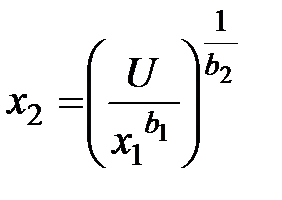Для расчёта параметров функции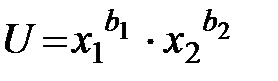 
целесообразно её линеаризовать посредством логарифмирования.
Имеем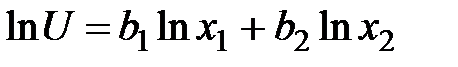 
.
Обозначим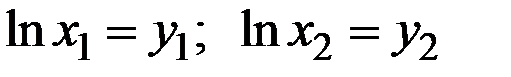 
и запишем
.
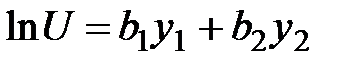Отсюда
.
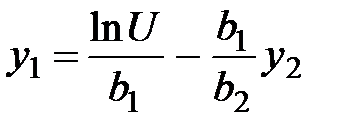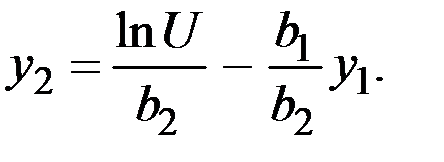
Обозначив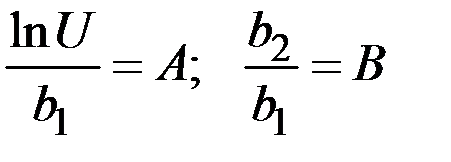 
, можно записать
.
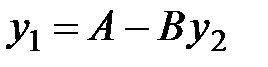Для определения коэффициентов A и B применим МНК:
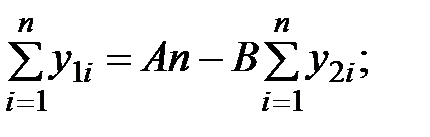
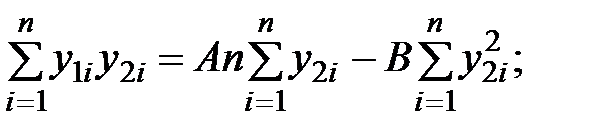
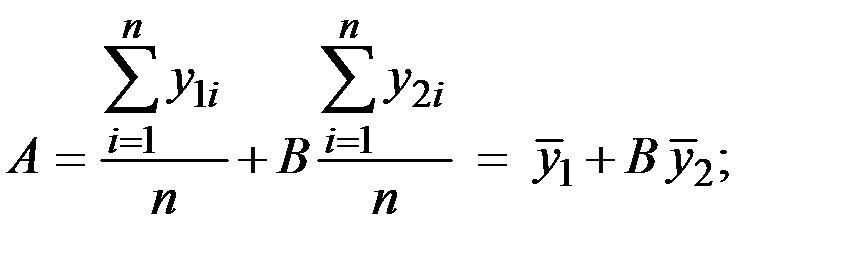
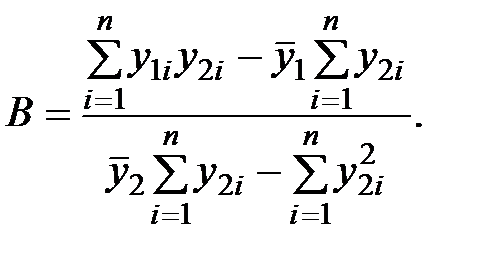
Учитывая, что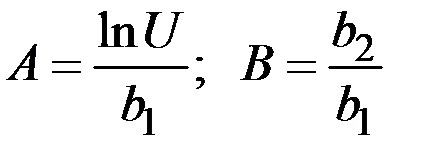 
определим
.
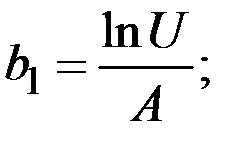
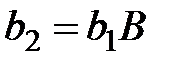Проверим правильность расчётов исследуемых зависимостей
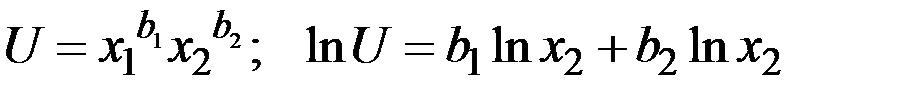
и определим расчётную кривую безразличия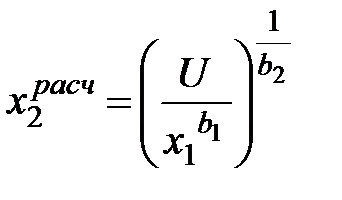 
,
отражающую отношения предпочтения, характерные для отдельного индивидуума.
На графике оптимальный план потребления соответствует точке касания бюджетной прямой и кривой безразличия.
Её координаты, т.е. значения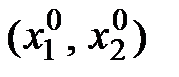 
, определяются путём нахождения частных производных функций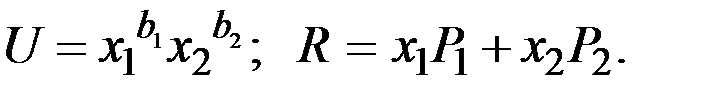 
После преобразований из модели Стоуна имеем функции спроса:
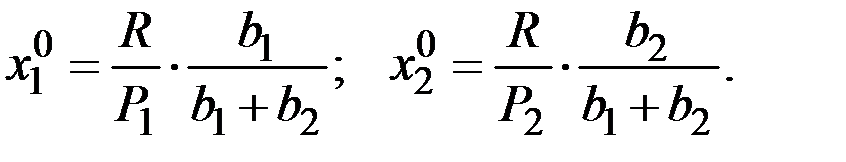
Они отражают оптимальный размер потребления продуктов, обеспечивающий максимум полезности в рамках бюджетного ограничения при заданных ценах.
При расчёте величин A и B можно воспользоваться таблицей вспомогательных расчётов.
Ниже приводятся расчёты для имеющихся данных (табл. 6.1).
Таблица 6.1
Расчёт функции безразличия
| i | х1i |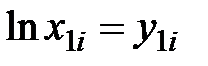 
| х2i |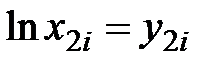 
| y1i y 2 i | y 2 i 2 |
| 1 | 2,9 | 1,065 | 13,5 | 2,603 | 2,772 | 6,776 |
| 2 | 3,0 | 1,099 | 12,0 | 2,485 | 2,731 | 6,175 |
| 3 | 5,0 | 1,609 | 7,5 | 2,015 | 3,242 | 4,060 |
| 4 | 7,0 | 1,946 | 6,0 | 1,792 | 3,487 | 3,211 |
| 5 | 10,0 | 2,303 | 5,0 | 1,609 | 3,706 | 2,589 |
| 6 | 12,0 | 2,485 | 4,5 | 1,504 | 3,737 | 2,262 |
| 7 | 12,3 | 2,509 | 4,6 | 1,526 | 3,829 | 2,329 |
| 
| 
| 
|
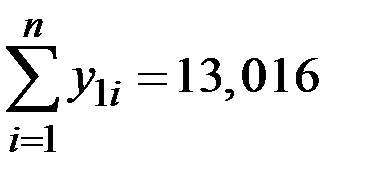
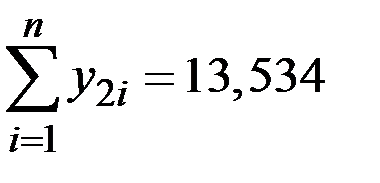
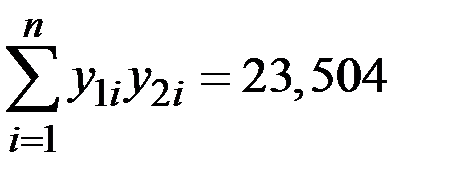
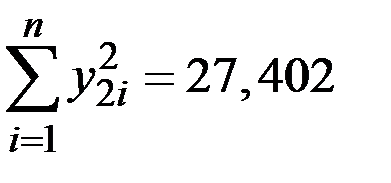
Определим коэффициенты A и B с использованием МНК:
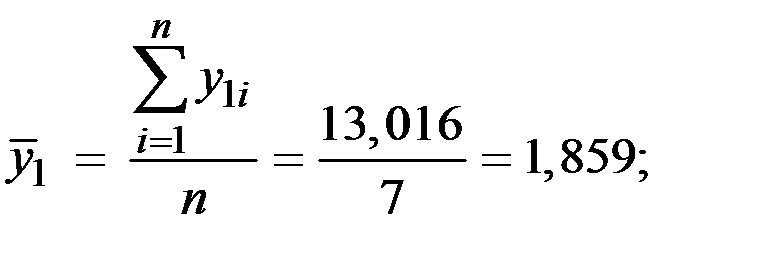
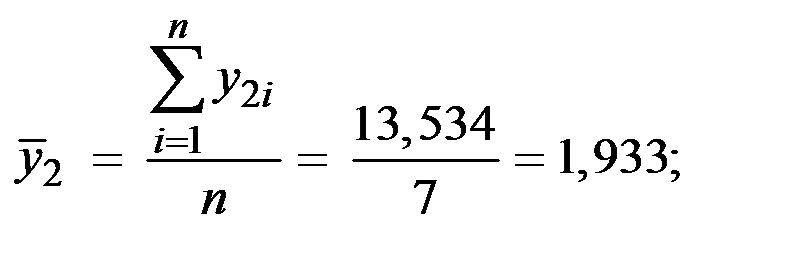
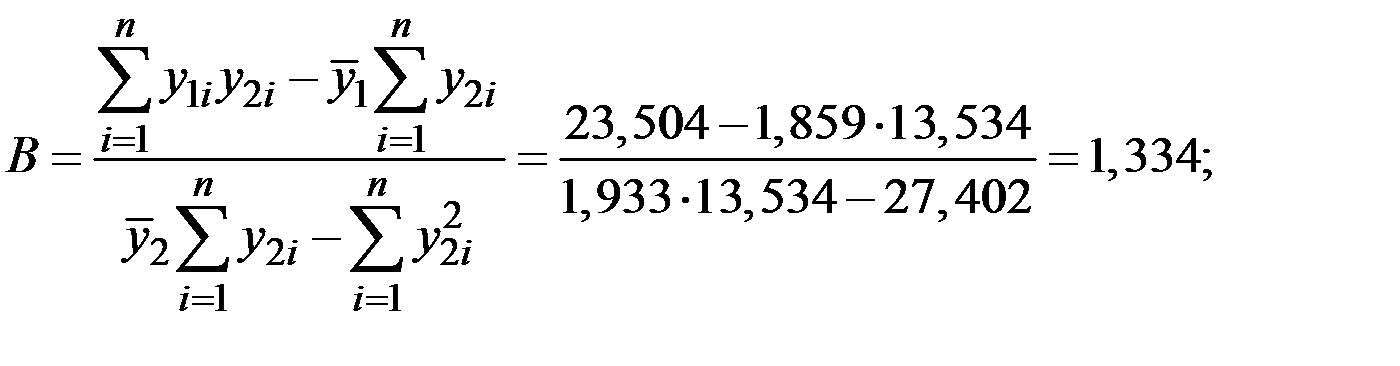
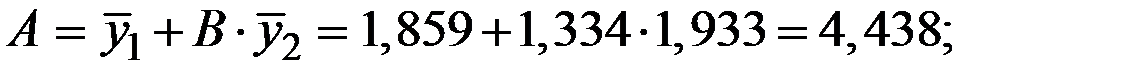
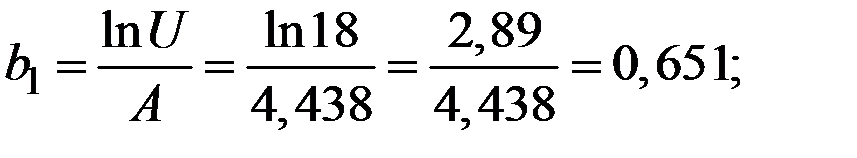
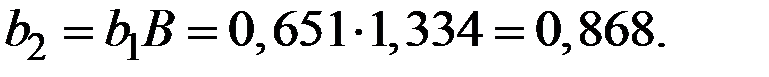
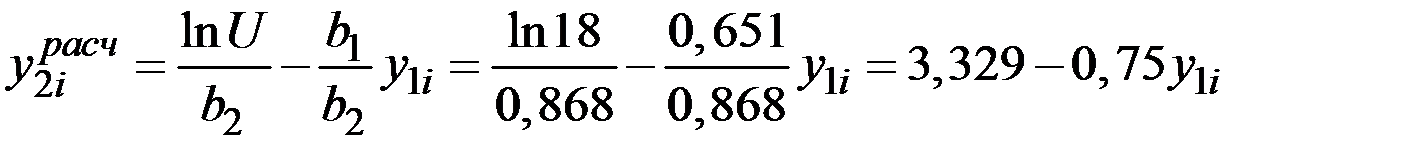
Таблица 6.2
Определение расчётной кривой безразличия
| i |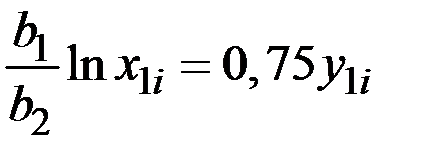 
| 
| 
| 
|
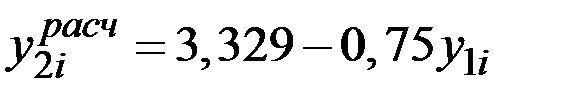
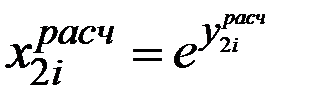
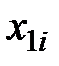
| 1 | 0,799 | 2,53 | 12,569 | 2,9 |
| 2 | 0,824 | 2,505 | 12,253 | 3,0 |
| 3 | 1,207 | 2,122 | 8,354 | 5,0 |
| 4 | 1,459 | 1,87 | 6,491 | 7,0 |
| 5 | 1,727 | 1,602 | 4,967 | 10,0 |
| 6 | 1,864 | 1,465 | 4,333 | 12,0 |
| 7 | 1,882 | 1,447 | 4,253 | 12,3 |
Окончательно получаем функцию спроса:
КОНТРОЛЬНЫЕ ВОПРОСЫ ПО ТЕМЕ 6
1. Что означает отношение предпочтения?
2. Каким свойствам должна удовлетворять функция полезности?
3. Каков экономический смысл свойств функции полезности? Приведите пример функции полезности.
4. Сформулируйте задачу потребительского выбора. Что такое целевая функция потребителя?
5. Что такое предельная полезность и предельная норма замещения?
6. Поясните графическое определение предельной полезности.
7. Сравните модели Стоуна и Слуцкого.
8. Что такое линии безразличия потребительского выбора?
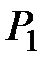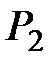Задание 6.1. На основании данных о потреблении взаимозаменяемых и взаимодополняемых продуктов x1 и x2 в различном сочетании i (табл. 6.3), их цене и , полезности U и бюджете (доходах) потребителя R (табл. 6.4) построить кривую безразличия и определить оптимальный план потребления названных продуктов.
Варианты заданий приведены в табл. 6.3 и табл. 6.4.
Таблица 6.3
Исходные данные о потреблении продуктов x1 и x2
|
№ n/n | ПРОДУКТЫ | |||||||||||||
| x1i | x2i | |||||||||||||
| i | i | |||||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| 1 | 1,9 | 2,0 | 3,0 | 6,0 | 13,0 | 13,5 | 14,0 | 13,4 | 12,5 | 4,0 | 2,5 | 2,0 | 1,9 | 1,7 |
| 2 | 5,9 | 6,0 | 9,9 | 14,0 | 20,0 | 24 | 25 | 13,6 | 12,0 | 7,5 | 6,0 | 5,0 | 4,5 | 4,6 |
| 3 | 4,9 | 5,0 | 7,0 | 10,0 | 14,0 | 17,0 | 17,2 | 18,0 | 17,0 | 12 | 7,5 | 5,0 | 4,5 | 4,4 |
| 4 | 1,1 | 1,2 | 1,5 | 3,0 | 8,0 | 10 | 14,0 | 14,0 | 12,0 | 8,0 | 3,0 | 1,2 | 1,1 | 1,1 |
| 5 | 2,1 | 2,2 | 2,4 | 4,0 | 9,0 | 11,0 | 13,0 | 14,0 | 12,0 | 8,0 | 4,0 | 2,0 | 1,3 | 1,2 |
| 6 | 1,3 | 1,4 | 1,7 | 4,0 | 8,5 | 10,0 | 15,0 | 14,0 | 11,0 | 9,0 | 4,0 | 1,3 | 1,2 | 1,1 |
| 7 | 2,2 | 2,5 | 3,0 | 5,0 | 7,0 | 11,0 | 14,0 | 13,0 | 11,0 | 9,0 | 5,0 | 4,0 | 2,5 | 2,1 |
| 8 | 1,1 | 1,2 | 2,0 | 6,0 | 8,0 | 12,0 | 14,0 | 13,0 | 11,0 | 7,0 | 2,8 | 2,0 | 1,5 | 1,3 |
| 9 | 1,1 | 1,2 | 1,5 | 3,0 | 8,0 | 11,0 | 14,2 | 14,0 | 12,0 | 8,0 | 4,0 | 2,0 | 1,3 | 1,2 |
| 10 | 22,0 | 28,0 | 32,0 | 42,0 | 47,4 | 47,6 | 47,8 | 24,4 | 24,3 | 24 | 23 | 20,8 | 20 | 17 |
| 11 | 2,2 | 2,3 | 3,3 | 6,2 | 13,3 | 13,8 | 14,2 | 13,7 | 12,8 | 4,0 | 2,8 | 2,3 | 2,2 | 2,0 |
| 12 | 3,9 | 4,0 | 6,0 | 8,0 | 11,0 | 13,0 | 13,3 | 14,5 | 13,0 | 8,5 | 7,0 | 6,0 | 5,5 | 5,6 |
| 13 | 5,4 | 5,5 | 7,5 | 10,5 | 14,5 | 17,5 | 17,7 | 18,5 | 17,5 | 12 | 8,0 | 5,5 | 5,0 | 4,9 |
| 14 | 1,4 | 1,5 | 1,8 | 3,3 | 8,3 | 10,3 | 14,3 | 14,3 | 12,3 | 8,3 | 3,3 | 1,5 | 1,4 | 1,4 |
| 15 | 1,9 | 2,0 | 2,2 | 3,8 | 8,8 | 10,8 | 12,8 | 13,8 | 11,8 | 7,8 | 3,8 | 1,8 | 1,1 | 1,0 |
| 16 | 1,4 | 1,5 | 1,8 | 4,1 | 8,6 | 10,1 | 15,1 | 14,1 | 11,1 | 9,1 | 4,1 | 1,4 | 1,3 | 1,2 |
| 17 | 2,1 | 2,4 | 2,9 | 4,9 | 6,9 | 10,9 | 13,8 | 13,9 | 11,7 | 9,2 | 5,2 | 3,8 | 2,5 | 2,3 |
| 18 | 21,8 | 27,8 | 32,7 | 40,9 | 45,4 | 46,5 | 46,6 | 23,6 | 23,3 | 23 | 22 | 21 | 20 | 17 |
| 19 | 1,6 | 1,9 | 2,3 | 6,4 | 8,1 | 12,0 | 14,1 | 13,0 | 11,5 | 7,2 | 3,2 | 2,0 | 1,9 | 1,7 |
| 20 | 2,1 | 2,2 | 2,5 | 4,0 | 9,0 | 11,0 | 15,0 | 15,0 | 13,0 | 9,0 | 5,0 | 3,0 | 2,3 | 2,2 |
| 21 | 2,9 | 3,0 | 4,0 | 7,0 | 14,0 | 14,5 | 15,0 | 14,4 | 13,5 | 5,0 | 3,5 | 3,0 | 2,9 | 2,7 |
| 22 | 2,5 | 2,6 | 5,6 | 7,4 | 9,5 | 11,4 | 11,8 | 12,0 | 11,6 | 7,0 | 5,4 | 4,0 | 4,1 | 4,0 |
| 23 | 3,9 | 4,0 | 6,0 | 9,0 | 13,0 | 16,0 | 16,2 | 17,0 | 16,0 | 11 | 6,5 | 4,0 | 3,5 | 3,4 |
| 24 | 1,0 | 1,1 | 1,4 | 3,0 | 8,0 | 10,0 | 14,0 | 14,0 | 12,0 | 8,0 | 3,0 | 1,1 | 1,0 | 1,0 |
| 25 | 1,1 | 1,2 | 1,4 | 3,0 | 8,0 | 10,0 | 12,0 | 13,0 | 11,0 | 7,0 | 3,0 | 1,3 | 1,1 | 1,1 |
| 26 | 1,5 | 1,6 | 1,9 | 4,2 | 8,8 | 10,2 | 15,2 | 14,2 | 11,2 | 9,2 | 4,2 | 1,5 | 1,4 | 1,3 |
Таблица 6.4
Цены и полезность продуктов. Доход потребителей
| № | ПОКАЗАТЕЛИ | |||
| варианта | U | P1 | P2 | R |
| 1 | 15 | 4 | 4,9 | 37 |
| 2 | 18 | 5 | 10,3 | 100 |
| 3 | 13 | 8 | 1,9 | 72 |
| 4 | 12 | 2 | 1,8 | 14 |
| 5 | 11 | 5 | 2,6 | 14 |
| 6 | 15 | 30 | 8,2 | 150 |
| 7 | 30 | 4 | 30,4 | 80 |
| 8 | 14 | 15 | 4,8 | 90 |
| 9 | 12 | 20 | 0,9 | 80 |
| 10 | 22 | 6 | 1,5 | 120 |
| 11 | 17 | 6 | 6,9 | 39 |
| 12 | 20 | 7 | 12,3 | 102 |
| 13 | 15 | 10 | 3,8 | 74 |
| 14 | 14 | 4 | 3,2 | 16 |
| 15 | 13 | 6 | 2,6 | 16 |
| 16 | 17 | 32 | 10,2 | 152 |
| 17 | 32 | 6 | 32,4 | 82 |
| 18 | 16 | 17 | 6,6 | 92 |
| 19 | 14 | 22 | 2,9 | 82 |
| 20 | 14 | 8 | 3,5 | 122 |
| 21 | 16 | 5 | 5,9 | 38 |
| 22 | 19 | 6 | 11,3 | 101 |
| 23 | 12 | 3 | 2,6 | 15 |
| 24 | 14 | 9 | 2,8 | 73 |
| 25 | 13 | 3 | 2,5 | 15 |
| 26 | 18 | 4 | 4,9 | 37 |
Задание 6.2. Дана функция полезности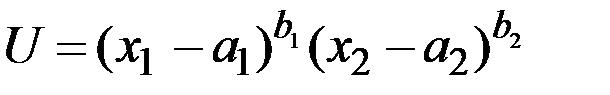 
, цены 
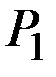и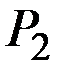 
, доход 
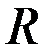. Найти точку локального рыночного равновесия потребителя. Пусть цена 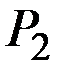увеличилось на 
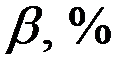. Найти новую точку локального равновесия. Сколько денег надо доплатить для того, чтобы не снизился уровень потребления (полезности, благосостояния). Найти структуру новый точки равновесия.
Исходные данные
| № Вар. | Параметры функции предпочтения | Цены продуктов | Доход
| Увеличение цены | ||||
| 
| 
| 
|
|
| |||
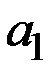
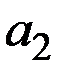
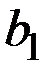
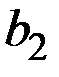
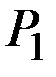
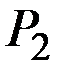
| 1 | 1,3 | 0,65 | 0,32 | 0,2 | 7,1 | 2,85 | 850 | 136 |
| 2 | 4,6 | 0,38 | 0,65 | 0,32 | 6,5 | 4,2 | 426 | 41 |
| 3 | 2,3 | 0,55 | 0,45 | 0,25 | 5,5 | 6,2 | 750 | 150 |
| 4 | 1,4 | 0,96 | 0,42 | 0,3 | 6,1 | 2,75 | 530 | 96 |
| 5 | 5,2 | 0,78 | 0,52 | 0,4 | 8,2 | 3,26 | 824 | 152 |
| 6 | 3,4 | 0,58 | 0,47 | 0,42 | 2,5 | 5,5 | 520 | 95 |
| 7 | 2,4 | 0,57 | 0,42 | 0,43 | 5,6 | 6,3 | 556 | 26 |
| 8 | 3,2 | 0,65 | 0,33 | 0,17 | 8,2 | 1,23 | 920 | 150 |
| 9 | 2,2 | 0,55 | 0,41 | 0,19 | 6,5 | 1,05 | 450 | 147 |
| 10 | 1,5 | 0,25 | 0,22 | 0,11 | 6,2 | 2,03 | 511 | 44 |
| 11 | 5,5 | 0,39 | 0,33 | 0,28 | 8,8 | 5,85 | 700 | 53 |
| 12 | 1,7 | 0,42 | 0,66 | 0,14 | 7,3 | 5,41 | 850 | 26 |
| 13 | 2,9 | 0,23 | 0,36 | 0,19 | 6,3 | 3,21 | 530 | 54 |
| 14 | 6,2 | 0,96 | 0,45 | 0,16 | 4,3 | 4,26 | 532 | 236 |
| 15 | 4,6 | 0,84 | 0,94 | 0,34 | 8,2 | 5,42 | 651 | 197 |
| 16 | 2,7 | 0,95 | 0,41 | 0,21 | 7,7 | 2,13 | 750 | 195 |
| 17 | 3,5 | 0,34 | 0,45 | 0,22 | 6,4 | 3,12 | 987 | 178 |
| 18 | 1,9 | 0,63 | 0,44 | 0,26 | 7,5 | 2,56 | 855 | 65 |
| 19 | 2,8 | 1,1 | 0,64 | 0,15 | 6,6 | 4,96 | 864 | 32 |
| 20 | 2,2 | 0,97 | 0,53 | 0,32 | 7,9 | 3,86 | 900 | 142 |
Задание 6.3. Целевая функция потребителя зависит от двух благ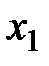 
и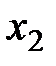 
следующим образом: 
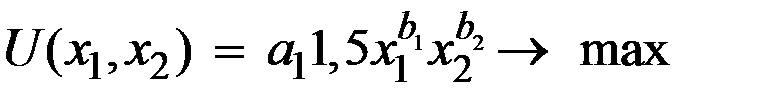. Известны цены благ ( 
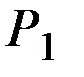и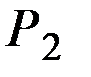 
) и доход потребителя 
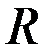. Найти точку локального рыночного равновесия потребителя. Пусть цена 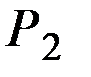становится равной 
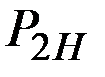. Каков необходимый размер компенсации? Какова новая структура потребительского набора?
Исходные данные
| № вар. | Параметры функции предпочтения | Цены продуктов | Доход
| Новая цена | |||
|
|
|
|
|
| |||
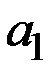
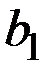
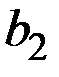
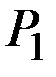
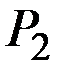
| 1 | 2,85 | 0,7 | 0,9 | 28 | 42 | 460 | 53 |
| 2 | 3,1 | 0,5 | 0,7 | 40 | 70 | 800 | 90 |
| 3 | 4,5 | 0,6 | 0,8 | 25 | 34 | 505 | 55 |
| 4 | 1,7 | 0,4 | 0,8 | 100 | 120 | 685 | 135 |
| 5 | 4 | 0,2 | 0,6 | 115 | 145 | 745 | 175 |
| 6 | 0,5 | 0,3 | 0,5 | 11 | 19 | 400 | 25 |
| 7 | 1,75 | 0,4 | 0,8 | 25 | 40 | 550 | 55 |
| 8 | 3 | 0,1 | 0,2 | 35 | 45 | 602 | 65 |
| 9 | 2,5 | 0,3 | 0,6 | 40 | 50 | 500 | 60 |
| 10 | 1,5 | 0,2 | 0,4 | 20 | 30 | 450 | 45 |
| 11 | 2,8 | 0,7 | 0,9 | 63 | 85 | 950 | 100 |
| 12 | 3,2 | 0,2 | 0,6 | 81 | 100 | 995 | 125 |
| 13 | 1,1 | 0,1 | 0,3 | 79 | 95 | 960 | 125 |
| 14 | 4,7 | 0,4 | 0,8 | 64 | 74 | 850 | 86 |
| 15 | 2,3 | 0,6 | 0,8 | 87 | 99 | 950 | 113 |
| 16 | 2 | 0,1 | 0,4 | 94 | 102 | 900 | 125 |
| 17 | 1,9 | 0,2 | 0,5 | 229 | 250 | 999 | 265 |
| 18 | 5 | 0,3 | 0,6 | 34 | 49 | 465 | 70 |
| 19 | 3,2 | 0,4 | 0,6 | 65 | 76 | 888 | 90 |
| 20 | 4,2 | 0,5 | 0,8 | 86 | 93 | 950 | 110 |
| 21 | 2,4 | 0,7 | 0,9 | 75 | 90 | 800 | 100 |
| 22 | 3,6 | 0,4 | 0,5 | 46 | 77 | 750 | 99 |
| 23 | 3,3 | 0,5 | 0,9 | 29 | 55 | 650 | 66 |
| 24 | 1 | 0,3 | 0,5 | 15 | 35 | 500 | 55 |
Дата: 2019-03-05, просмотров: 320.
