Основные понятия
Пусть потребитель располагает доходом R, который он полностью тратит на приобретение определённого количества благ (продуктов)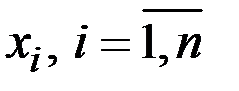 
. Цены благ ( 
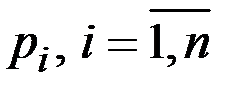) считаются заданными.
Потребитель приобретает определённые количества благ, учитывая структуру цен, доход и собственные предпочтения.
Математическая модель поведения потребителя в такой ситуации называется моделью потребительского выбора.
Потребитель решает статическую задачу, то есть в модели не учитываются его межвременные предпочтения и возможности делать или расходовать сбережения.
Рассмотрим модель с двумя видами благ.
Такая модель удобна возможностью графической интерпретации, сохраняя при этом все принципиальные свойства общей модели.
Потребительский набор – это вектор (x1, x2), координата x1 которого равна количеству единиц первого блага, а координата x2 равна количеству единиц второго блага.
Выбор потребителя (индивидуума) характеризуется отношением предпочтения. Считается, что потребитель про каждые 2 набора может сказать, что либо один из них более желателен, чем другой, либо потребитель не видит между ними разницы.
Отношение предпочтения транзитивно, т.е. если набор A = (a1, a2), предпочтительнее набора B = (b1, b2), а набор B предпочтительнее набора C = (c1, c2), то набор A предпочтительнее набора C.
На множестве потребительских наборов (x1, x2) определена функция U(x1,x2) (называемая функцией полезности потребителя), значение которой на потребительском наборе (x1, x2) равно потребительской оценке полезности для индивидуума этого набора.
Потребительскую оценку U(x1, x2) набора (x1, x2) принято называть уровнем (степенью) удовлетворения потребностей индивидуума, если он приобретает или потребляет данный набор (x1, x2).
Каждый потребитель имеет свою функцию полезности.
Если набор A предпочтительнее набора В, то U(A) > U(B).
Функция полезности удовлетворяет следующим свойствам.
1. Возрастание потребления одного продукта при постоянном потреблении другого продукта ведёт к росту потребительской оценки, т.е. первые частные производные функции полезности по своим аргументам положительны:
,
.
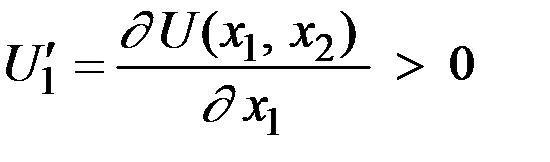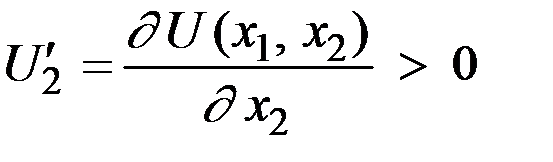Это свойство должно выполняться всегда.
Первые частные производные называются предельными полезностями продуктов:
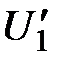называется предельной полезностью первого продукта,
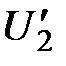– предельной полезностью второго продукта.
2. Закон убывания предельной полезности: предельная полезность каждого продукта уменьшается, если объём его потребления растёт.
Математически это означает отрицательность вторых производных:
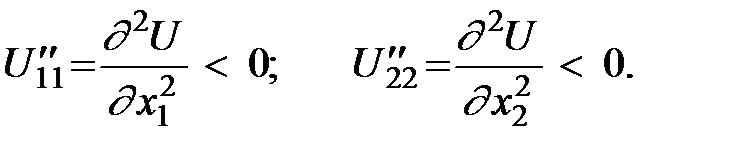
3. Предельная полезность каждого продукта увеличивается, если растёт количество другого продукта.
В этом случае продукт, количество которого фиксировано, оказывается относительно дефицитным.
Поэтому дополнительная его единица приобретает большую ценность и может быть потреблена более эффективно.
Данное свойство не столь очевидно, как первые два, и справедливо не для всех благ. Если блага могут полностью замещать друг друга в потреблении, то свойство 3 не выполняется.
Предположение 3 вводится не всегда, но оно гарантирует выпуклость вниз линий безразличия, т.е.
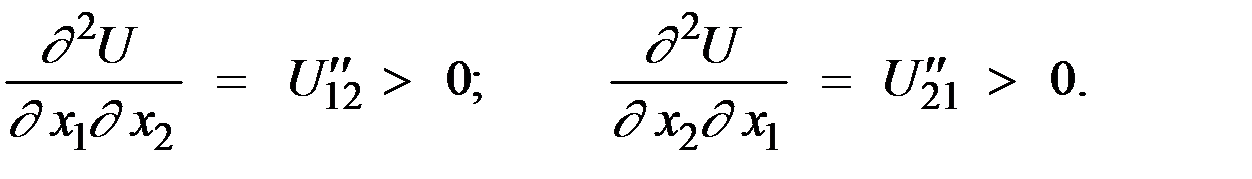
Линия, соединяющая потребительские наборы (x1, x2), имеющие один и тот же уровень удовлетворения потребностей индивидуума, называется линией безразличия.
Это и есть линия уровня функции полезности.
Множество линий безразличия называется картой линий безразличия. Линии безразличия, соответствующие разным уровням удовлетворения потребностей, не касаются и не пересекаются.
Если линия безразличия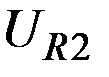 
, соответствующая полезности (тратам) 
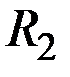, расположена выше и правее ("северо–восточнее") линии безразличия 
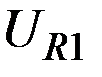, то 
.
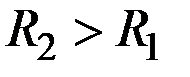Верно и обратное.
Иными словами. чем "северо–восточнее" расположена линия безразличия, тем большему уровню удовлетворения потребности она соответствует.
Линия безразличия убывает (является нисходящей) и строго выпукла к началу координат.
Рассмотрим фиксированную линию безразличия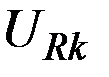 
.
Пусть потребительский набор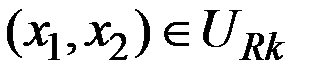 
.
При выполнении ряда естественных предположений (непрерывность первых частных производных ,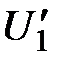 
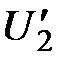и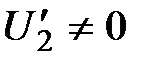 
) справедлива формула:
.
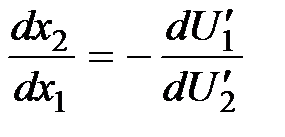Имеем приближённое равенство (рис. 6.1)
.
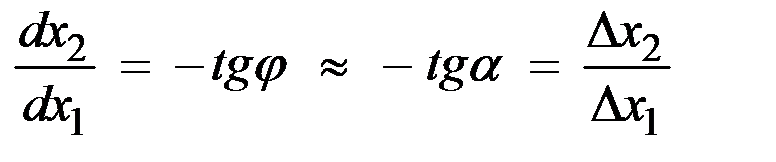Следовательно: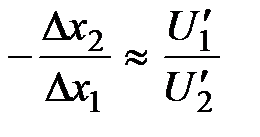 
.
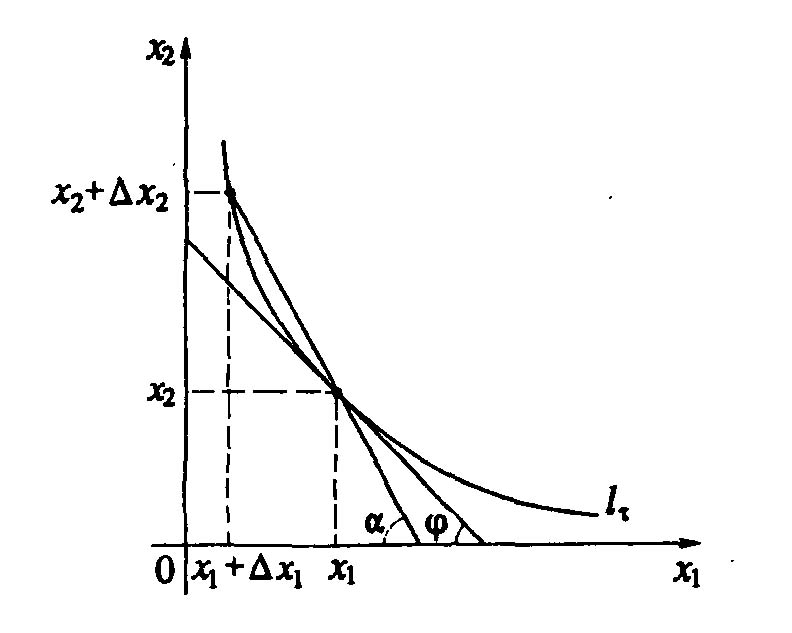
Рис. 6.1. Графическая интерпретация свойств линии безразличия
Отношение (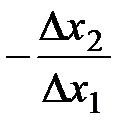 
) показывает, на сколько должен индивидуум увеличить (уменьшить) потребление второго продукта, если он уменьшил (увеличил) потребление первого продукта на одну единицу без изменения уровня удовлетворения своих потребностей.
Геометрически это означает, что точки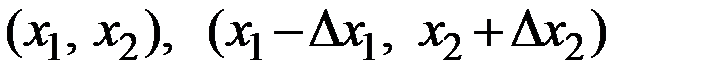 
принадлежат одной и той же линии безразличия .
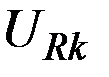Дробь ( 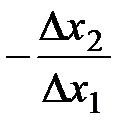) принято называть нормой замены первого продукта вторым на потребительском наборе (x1, x2).
Производную (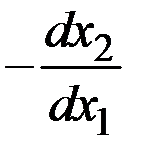 
) (которая равна предельному значению дроб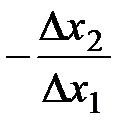и при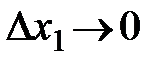 
) принято называть предельной нормой замены первого продукта вторым.
Предельная норма замещения набора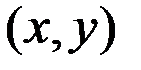 
часто обозначается 
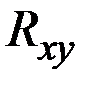или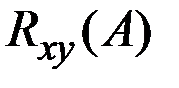 
, если необходимо явно указать её зависимость от точки А.
Примером функции полезности может служить функция
,
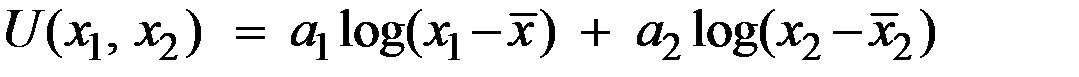где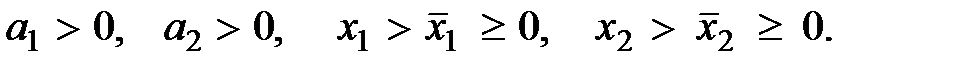 
Для неё справедливы свойства 1 и 2 функции полезности.
Свойство 3 не выполнено, так как смешанные вторые частные производные функции U(x1,x2) равны нулю.
Пример 6.1. Найти предельную норму замещения х на у для функции полезности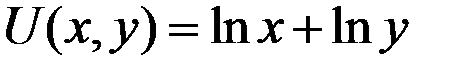 
в точках: 1) А(3;12), 2) В(2;1).
Решение.
1) В первой точке А получаем
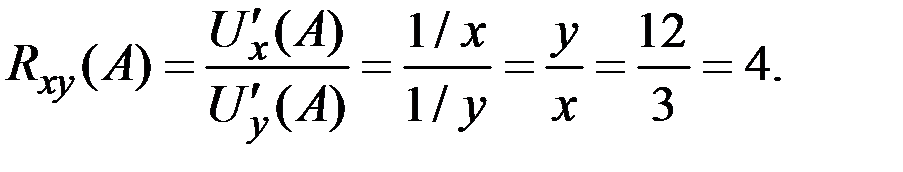
2) Аналогично во второй точке В находим
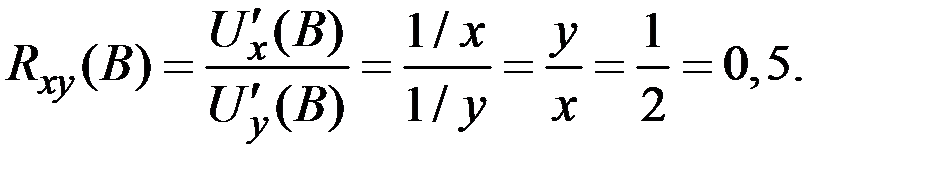
Задача потребительского выбора (задача рационального поведения потребителя на рынке) заключается в выборе такого потребительского набора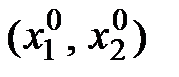 
, который максимизирует его функцию полезности при заданном бюджетном ограничении.
Бюджетное ограничение означает, что денежные расходы на продукты не могут превышать денежного дохода, т.е.
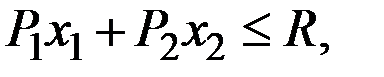
где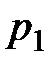 
и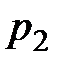 
– рыночные цены одной единицы первого и второго продуктов соответственно,
R – доход индивидуума, который он готов потратить на приобретение первого и второго продуктов.
Величины 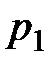, 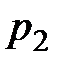и R считаются заданными.
Формально задача потребительского выбора имеет вид:
;
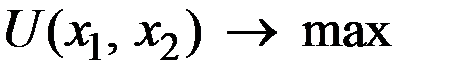при условиях
; 
.
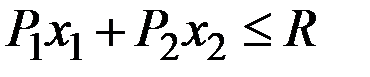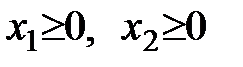Допустимое множество (множество наборов благ x1 и x2, доступных для потребителя) представляет собой треугольник, ограниченный осями координат и бюджетной прямой (рис. 6.2).
На этом множестве требуется найти точку, принадлежащую кривой безразличия с максимальным уровнем полезности.
Поиск этой точки можно интерпретировать графически как последовательный переход на линии всё более высокого уровня полезности (вправо вверх) до тех пор, пока эти линии ещё имеют общие точки с допустимым множеством.
Рис. 6.2. Определение оптимального набора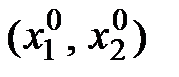
Набор 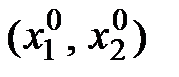, который является решением задачи потребительского выбора, принято называть оптимальным для потребителя, или локальным рыночным равновесием потребителя.
Отметим свойства задачи потребительского выбора.
1. Решение задачи 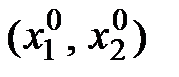сохраняется при любом монотонном преобразовании функции полезности U(x1, x2).
Таким монотонным преобразованием может быть умножение функции полезности на некоторое положительное число, возведение её в положительную степень, логарифмирование по основанию, большему единицы. Поскольку значение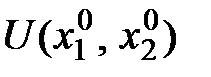 
было максимальным на всём допустимом множестве, оно остаётся таковым и после монотонного преобразования функции полезности (допустимое множество, определяемое бюджетным ограничением, остаётся неизменным).
2. Решение задачи выбора не изменится, если все цены и доход увеличиваются (уменьшаются) в одно и то же число раз l .
Это равнозначно умножению на положительное число l обеих частей бюджетного ограничения 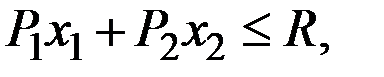что даёт неравенство, эквивалентное исходному. Поскольку ни цены, ни доход R не входят в функцию полезности, задача остаётся той же, что и первоначально.
В приведённой постановке задача потребительского выбора является задачей нелинейного программирования.
Однако, если на каком–то потребительском наборе (x1, x2) бюджетное ограничение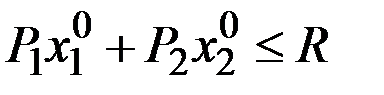 
будет выполняться в виде строгого неравенства, то мы можем увеличить потребление какого–либо из продуктов и тем самым увеличить функцию полезности.
Следовательно, набор 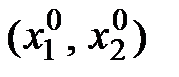, максимизирующий функцию полезности, должен обращать бюджетное ограничение в равенство, т.е.
.
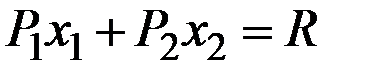Графически (рис. 6.2) это означает, что решение 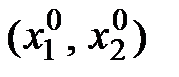задачи потребительского выбора должно лежать на бюджетной прямой, которую удобнее всего провести через точки пересечения с осями координат, где весь доход тратится на один продукт: 
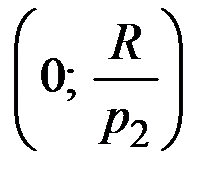и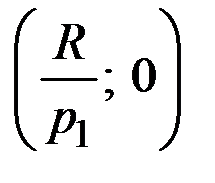 
.
Будем также считать, что в оптимальной точке 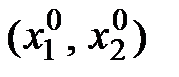условия положительности величин x1 и x2 выполняются автоматически, вытекая из свойств функции 
.
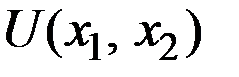В то же время, если условия неотрицательности переменных не включать в явном виде в условие задачи, то она становится существенно проще с математической точки зрения.
Задачу потребительского выбора можно заменить задачей на условный экстремум, так как решение 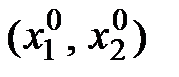этих двух задач одно и то же:
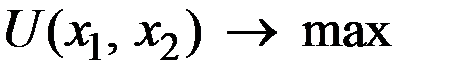
при условиях ;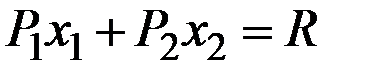 
.
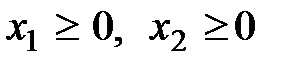Для решения задачи на условный экстремум применим метод Лагранжа.
1) Выписываем функцию Лагранжа
.
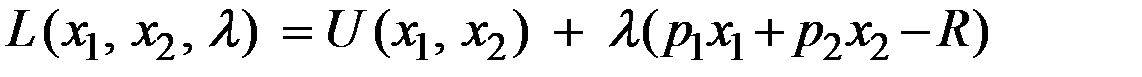2) Находим её первые частные производные по переменным x1, x2, l и приравниваем эти частные производные к нулю:
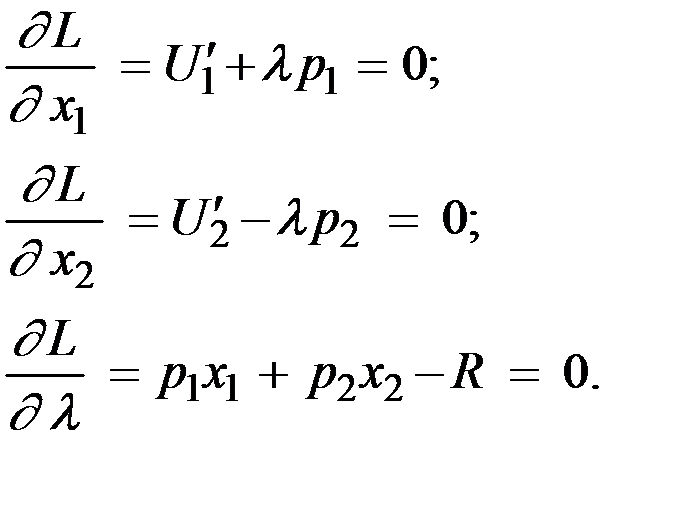
Исключив из полученной системы трёх уравнений с тремя неизвестными величину l (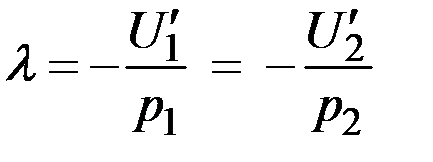 
), получим систему двух уравнений с двумя неизвестными 
: 
;
.
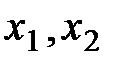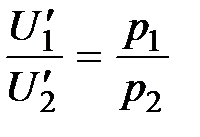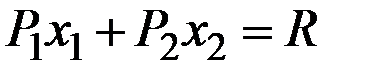Решение 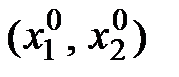этой системы есть решение задачи потребительского выбора. Подставив решение 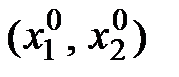в левую часть равенства
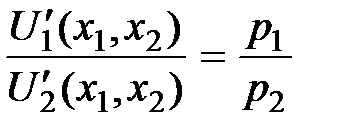
получим, что в точке 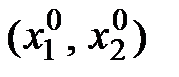локального рыночного равновесия индивидуума отношение предельных полезностей продуктов равно отношению рыночных цен 
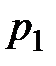и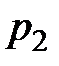 
на эти продукты:
.
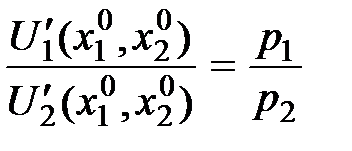В связи с тем, что отношение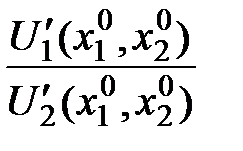 
равно предельной норме замены первого продукта вторым в точке локального рыночного равновесия 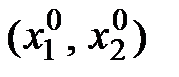, то следует, что эта предельная норма равна отношению рыночных цен 
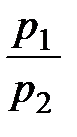на продукты.
Геометрически решение 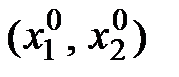можно интерпретировать как точку касания линии безразличия функции полезности 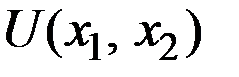с бюджетной прямой .
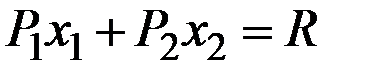Это определяется тем, что отношение
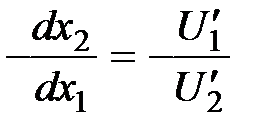
показывает тангенс угла наклона линии уровня функции полезности, а отношение (–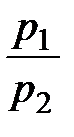 
) представляет тангенс угла наклона бюджетной прямой.
Поскольку в точке оптимального потребительского выбора (или локального рыночного равновесия) они равны, в этой точке происходит касание данных двух линий.
Следовательно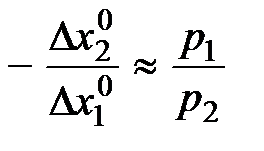 
.
Отношение (со знаком минус) конечных (относительно небольших) изменени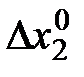й 
и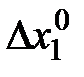 
объёмов продуктов в локальном рыночном равновесии 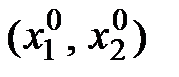приближённо равно отношению рыночных цен p1, p2 на продукты.
Последнее равенство позволяет давать приближённые оценки отношению рыночных цен, если известны конечные изменения объёмов продуктов относительно потребительского набора, приобретённого потребителем, т.е. набора, который естественно следует толковать в качестве оптимального для потребителя.
Координаты решения 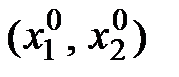задачи потребительского выбора есть функции параметров p1, p2 и R:
,
.
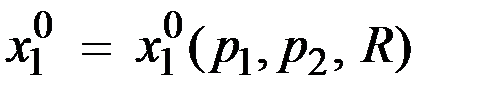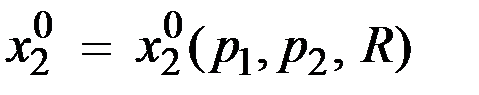Полученные функции называются функциями спроса на первый и второй продукты.
Важным свойством функций спроса является их однородность нулевой степени относительно цен и дохода, т.е. значения функций спроса инвариантны по отношению к пропорциональным изменениям цен и дохода (для любого числа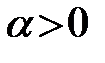 
):
;
.
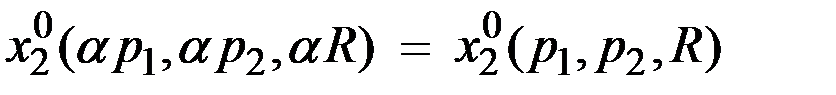Это означает, что если все цены и доход изменятся в одно и то же число раз, величина спроса на продукт (первый или второй – безразлично) останется неизменной.
Дата: 2019-03-05, просмотров: 492.
