Рассмотрим эту модель на примере.
Пример 5.4. Пусть имеются три конкурирующих изделия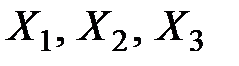 
.
С целью определения спроса на эти изделия произведён опрос 100 человек. Оказалось, что изделие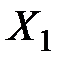 
покупает 50 человек, изделие 
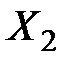– 20 человек, а 
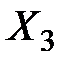– 30 человек.
Предположим, что поведение покупателей в каждый следующий месяц обусловлено только их поведением в предыдущий месяц (таким образом, исследуется простая цепь Маркова).
По истечении месяца оказалось, что из 50 человек, покупавших изделие 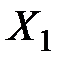, 45 человек продолжают его покупать, 4 человека стали покупать изделие 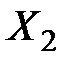и 1 – изделие 
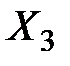. Из 20 человек, покупавших изделие 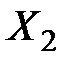, 6 человек продолжают его покупать, 8 стали покупать изделие 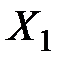, 6 – изделие 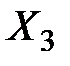. Из 30 человек, покупавших изделие 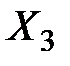, 6 человек продолжают его покупать, 21 человек стал покупать изделие 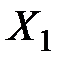, 3 – изделие .
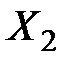Требуется определить, какое изделие будет пользоваться наибольшим спросом по истечении месяца? Через 2 месяца? Через год?
Решение. Если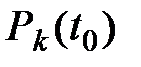 
– вероятности потребности в изделии 
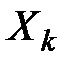в момент 
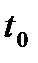, то из условий задачи 
.
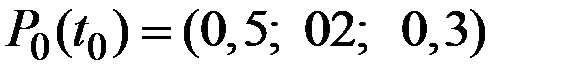Переходные вероятности определяются из условия задачи (рис. 5.2):
;
;
.
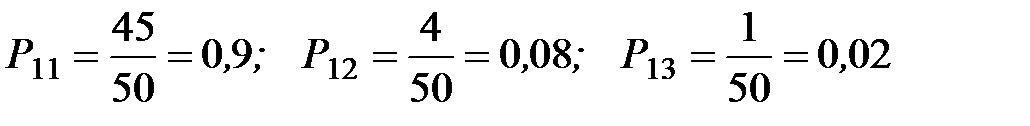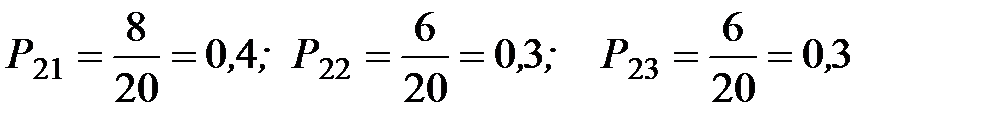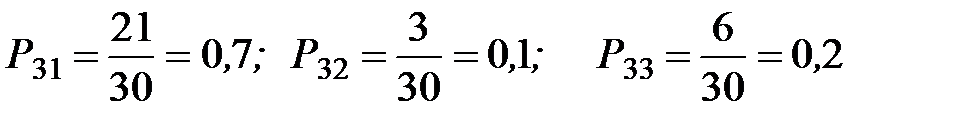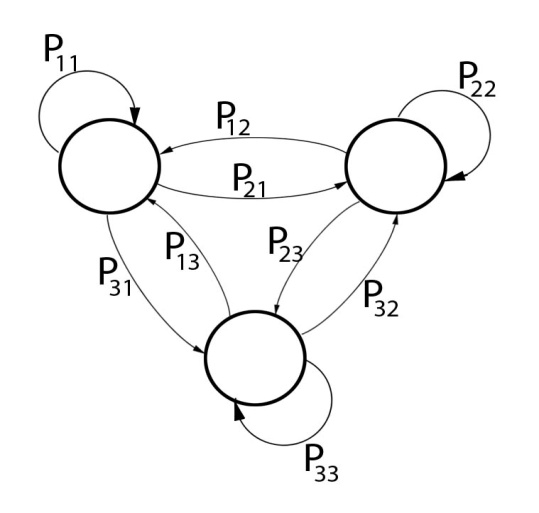
Рис. 5.2. Граф переходов и состояний системы
Искомые вероятности получаются умножением вектора вероятностей состояния цепи Маркова на переходную матрицу вероятностей:
,
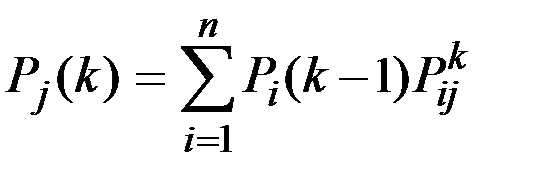где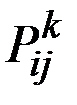 
– вероятность перехода системы из i–го состояния в j–е на k–м шаге.
Получаем вероятности спроса изделий для первого месяца:
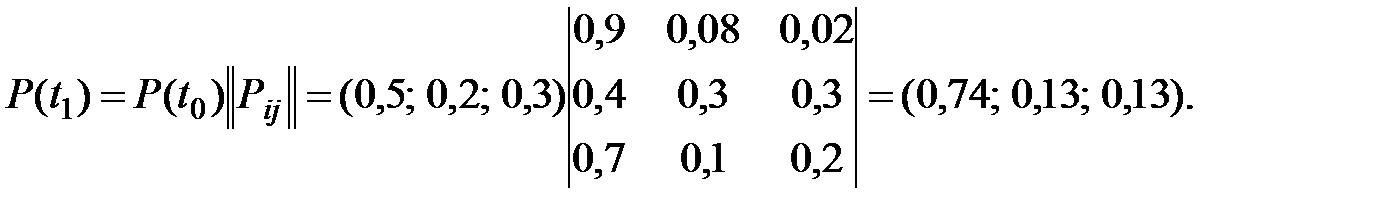
Через месяц наибольшим спросом будет пользоваться изделие .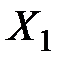
Если предположить, что поведение покупателей со временем не меняется, т.е. что цепь однородна по времени, то аналогично можно определить, какое изделие будет пользоваться наибольшим спросом по истечении двух, трёх т.д. месяцев. Вероятности спроса изделий через два месяца:
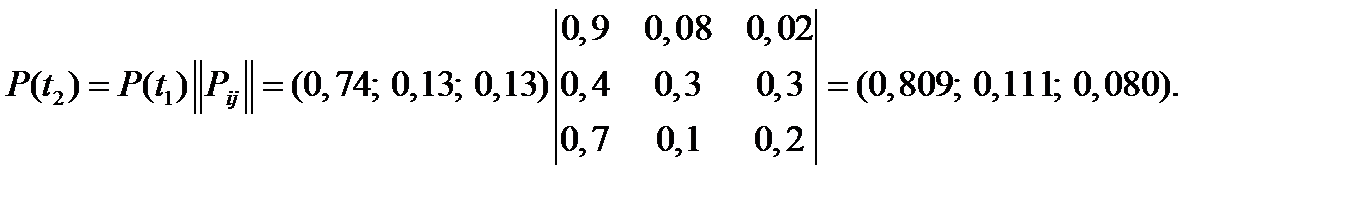
Определим, какое изделие будет пользоваться наибольшим спросом по истечении достаточно продолжительного периода (год).
Все элементы матрицы перехода положительны, т.е. условие эргодичности выполняется, следовательно, предельные вероятности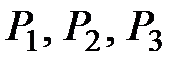 
потребления изделий 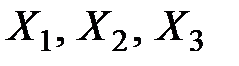существуют.
Система уравнений в данном случае имеет вид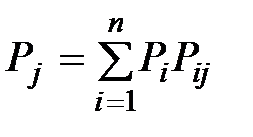 
, т.е.
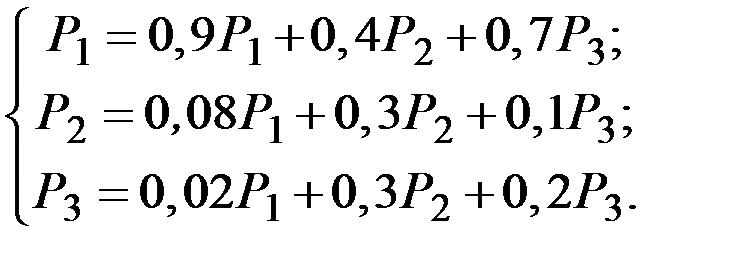
Система линейно зависима. Заменяя третье уравнение системы уравнением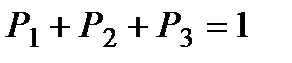 
, получим систему
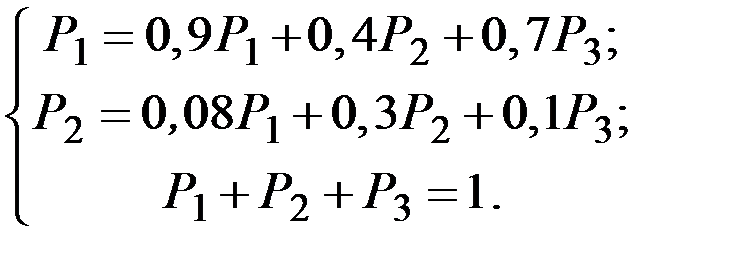
Решение системы:
.
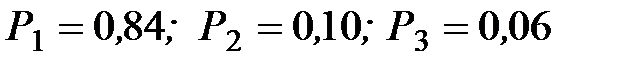Моделирование потребления
Экономико–математические построения, описывающие взаимосвязи и зависимости между потреблением и определяющими его факторами, относятся к моделям потребления.
Модели потребления используются для анализа динамики потребления за прошедший период, построения его прогнозов на перспективу разной продолжительности.
Наибольшее распространение в практике аналитических и прогнозных расчётов получили модели потребления, построенные на основе регрессионного анализа: в уравнении регрессии в качестве функции выступает объём потребления, а в качестве независимых переменных – определяющие его факторы.
Модели потребления для случая линейной связи между потреблением и определяющими его факторами имеют вид
,
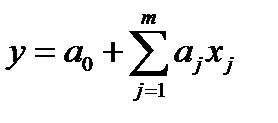где у – потребление конкретного вида товара или агрегата товаров;
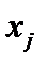– учтённые в модели факторы;
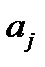– параметры модели.
Если анализу подлежит общий объём потребления населением товаров и услуг, то в качестве определяющих факторов в модель могут быть включены: общий объём валового внутреннего продукта; величина денежных доходов населения; индекс розничных цен на потребительские товары и индекс тарифов на платные услуги.
Если же моделируется потребление отдельных товаров, то в модель достаточно включать факторы, характеризующие доходы населения, цены соответствующих товаров, и, возможно, ещё некоторые факторы, отбираемые в соответствии с особенностями данного товара.
Свою специфику имеет построение моделей потребления технически сложных товаров длительного пользования.
Она зависит от того, в каких показателях исчисляется их потребление.
Если используются показатели годового объёма продажи товаров, то в обычную регрессионную модель потребления достаточно ввести дополнительно фактор научно–технического качества, который оказывает ощутимое влияние на уровень продажи этих товаров.
Этот фактор может выражаться с помощью различных показателей, но чаще всего используется доля новых марок технически сложных товаров длительного пользования определённого вида (например, телевизоров, холодильников, стиральных машин) в общем объёме производства.
Чаще всего (в том числе и в международных сопоставлениях) потребление товаров длительного пользования характеризуется показателем обеспеченности населения ими в расчёте на каждые 100 семей или 1000 человек.
В этом случае для анализа и прогнозирования потребления товаров длительного пользования применяются модели, в основе которых лежат логистические функции вида:
,
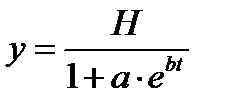где у – уровень обеспеченности населения данным товаром;
H – верхний предел уровня обеспеченности этим товаром;
t – время;
е – основание натуральных алгоритмов;
a, b – параметры модели.
В конкретных случаях в формулу логистической функции вводятся различные дополнительные переменные и параметры в соответствии со спецификой задачи.
При выполнении практических прогнозных расчётов уровня обеспеченности с помощью логистических функций важную роль играет определение верхнего предела обеспеченности H.
Обычно в качестве значения H берутся либо рациональные нормативы обеспеченности, либо точки насыщения, после достижения которых дальнейший рост обеспеченности семей данным видом товаров длительного пользования не происходит.
КОНТРОЛЬНЫЕ ВОПРОСЫ ПО ТЕМЕ 5
1. Охарактеризуйте этапы построения прогнозных моделей.
2. Как оценить точность прогнозных моделей?
3. Как оценить адекватность прогнозных моделей?
4. Как проверить на значимость коэффициенты модели?
5. Поясните особенности адаптивных методов прогнозирования.
6. Поясните суть метода наименьших квадратов.
7. Сравните разновидности адаптивных методов прогнозирования.
8. Как сравнить влияние различных факторов на результирующую переменную?
9. В чём заключаются задачи моделирования изучения спроса?
10. В чём заключаются особенности моделирования спроса на основе марковских процессов?
11. Поясните виды спроса и факторы влияния на них.
12. Приведите примеры использования однофакторных и многофакторных моделей спроса.
Задание 5.1. Фирма выпустила на рынок три конкурирующих (взаимозаменяемых) изделия. С целью определения спроса на эти изделия произведён опрос покупателей. Оказалось, что из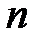 
человек 
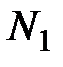покупает первое изделие, 
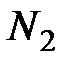– второе, 
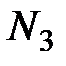– третье ( 
).
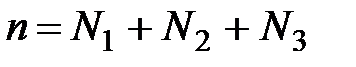Повторный опрос этих же покупателей через неделю показал, что из 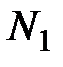человек, покупавших первое изделие 
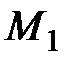продолжают его покупать, 
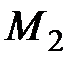стали покупать второе изделие, остальные – третье.
Из 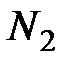человек, покупавших второе изделие, продолжают его покупать 
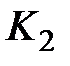человек, 
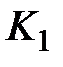стали покупать первое изделие, остальные – третье.
Из 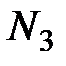человек, покупавших третье изделие, 
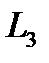человек продолжают его покупать, 
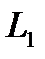и 
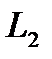– стали покупать соответственно первое и второе (табл. 5.15). Определить, какое изделие будет пользоваться наибольшим спросом: 1) через неделю; 2) через две недели; 3) через год.
Варианты значений параметров задачи приведены в табл. 5.15.
Таблица 5.15
Варианты значений параметров
| № вар. |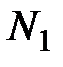
|
|
|
|
|
|
| 
| 
|
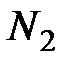
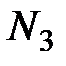
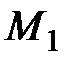
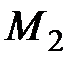
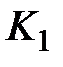
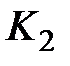
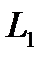
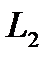
| 1 | 80 | 8 | 12 | 65 | 8 | 5 | 2 | 6 | 4 |
| 2 | 60 | 10 | 15 | 35 | 25 | 4 | 5 | 5 | 8 |
| 3 | 50 | 40 | 10 | 20 | 30 | 10 | 15 | 4 | 5 |
| 4 | 40 | 70 | 90 | 10 | 30 | 15 | 45 | 40 | 20 |
| 5 | 30 | 80 | 190 | 10 | 15 | 30 | 40 | 10 | 15 |
| 6 | 50 | 20 | 30 | 20 | 25 | 8 | 10 | 4 | 6 |
| 7 | 60 | 30 | 110 | 50 | 6 | 8 | 15 | 20 | 30 |
| 8 | 70 | 20 | 60 | 35 | 15 | 4 | 13 | 15 | 25 |
| 9 | 80 | 45 | 180 | 70 | 4 | 16 | 20 | 40 | 60 |
| 10 | 90 | 20 | 60 | 80 | 6 | 7 | 11 | 10 | 20 |
| 11 | 120 | 100 | 40 | 70 | 30 | 15 | 80 | 15 | 5 |
| 12 | 150 | 50 | 20 | 100 | 35 | 3 | 40 | 7 | 8 |
| 13 | 130 | 70 | 100 | 90 | 25 | 7 | 60 | 15 | 40 |
| 14 | 140 | 85 | 75 | 75 | 45 | 10 | 70 | 20 | 30 |
| 15 | 160 | 40 | 100 | 105 | 35 | 8 | 30 | 35 | 5 |
| 16 | 170 | 200 | 130 | 100 | 40 | 40 | 150 | 30 | 40 |
| 17 | 180 | 400 | 120 | 95 | 45 | 80 | 230 | 25 | 60 |
| 18 | 200 | 40 | 160 | 110 | 60 | 4 | 32 | 65 | 70 |
| 19 | 80 | 70 | 50 | 30 | 20 | 40 | 25 | 14 | 16 |
| 20 | 30 | 40 | 130 | 25 | 2 | 10 | 20 | 20 | 100 |
| 21 | 35 | 80 | 15 | 30 | 3 | 16 | 50 | 4 | 9 |
| 22 | 70 | 50 | 80 | 40 | 10 | 10 | 32 | 20 | 50 |
| 23 | 150 | 40 | 70 | 105 | 25 | 14 | 20 | 40 | 20 |
| 24 | 40 | 200 | 160 | 25 | 5 | 40 | 120 | 40 | 100 |
| 25 | 170 | 150 | 180 | 140 | 10 | 110 | 32 | 20 | 50 |
| 26 | 72 | 20 | 60 | 35 | 15 | 4 | 13 | 15 | 25 |
| 27 | 80 | 47 | 180 | 70 | 4 | 16 | 20 | 40 | 60 |
Задание 5.2. По имеющемуся тренд–сезонному временному ряду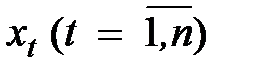 
получить прогнозную мультипликативную модель Хольта–Уинтерса и выполнить прогноз ряда на один временной шаг. Необходимо:
1. Методом наименьших квадратов или графически по первым l значениям временного ряда оценить начальные значения параметров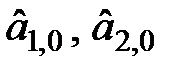 
.
2. Начальное значение коэффициентов сезонности получить делением первых l фактических значений ряда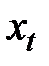 
на их оценки, вычисленные по линейной модели 
; 
.
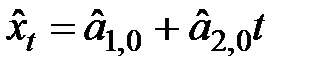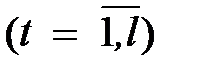3. Параметры сглаживания принять равными: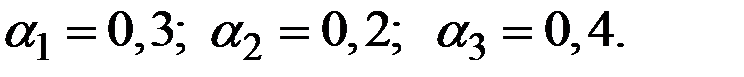 
4. По формулам мультипликативной модели Хольта–Уинтерса произвести расчёт параметров и значений показателя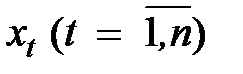 
, начиная с 
.
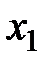5. Составить таблицу и графики динамики изменения параметров:
.
6. Вычислить ошибки расчётов: среднюю арифметическую, среднюю квадратическую, среднюю по модулю.
7. Сделать прогноз ряда на один шаг вперёд; т.е. получить значение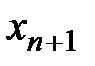 
.
8.Составить ретропрогноз на последний цикл ряда.
9. Исследовать адекватность полученной модели.
10. Исходным данным дать физическое толкование и проанализировать полученные результаты.
Ниже приведены варианты значений экономических рядов.
Вариант № 1: 12,6; 24,1; 40,4; 12,8; 13,7; 24,7; 42,7; 12,6; 13,4; 25,2; 50,1; 15,2; 14,4; 27,3; 53,6; 15,7; 15,9; 29,4; 58,8; 16,4.
Вариант № 2: 28; 22; 20; 24; 27; 29; 27; 25; 30; 32; 33; 27; 26; 28; 32; 34; 29; 30; 33; 35; 36; 31; 30; 37; 38.
Вариант № 3: 8,3; 8,7; 10,3; 10,7; 9,9; 8,6; 8,9; 9,1; 10,9; 10,8; 10,2; 8,9; 9,4; 9,7; 11,2; 11; 9,4; 9,3; 10,2; 10,1; 11,1; 12,2; 10,4; 9,7.
Вариант № 4: 10,7; 9,9; 8,6; 8,9; 9,1; 10,9; 10,8; 10,2; 8,9; 9,4; 9,7; 11,2; 11; 9,4; 9,3; 10,2; 10,1; 11,1; 12,2; 10,4; 9,7.
Вариант № 5: 62,03; 69,9; 78,11; 89,14; 99,29; 111,06; 114,89; 130,13; 144,04; 166,13; 176,97; 185,06; 195,42; 202,34; 207,92; 214,57; 242,96.
Вариант № 6: 7,9; 9,2; 10,2; 10,8; 9,9; 8,8; 8,3; 8,7; 10,3; 10,7; 9,9; 8,6; 8,9; 9,1; 10,9; 10,8; 10,2; 8,9; 9,4; 9,7; 11,2.
Вариант № 7: 3; 3,8; 3,1; 3,2; 3,4; 4,7; 4,2; 4,9; 5; 5,7; 5,2; 5,1.
Вариант № 8: 19,7; 20,4; 22,8; 20,7; 21,2; 22,3; 23,4; 20,3; 20,7; 22,1; 22,7; 21,1; 21,2; 23,7; 24,2; 21,4; 21,6; 25,4; 26,5; 22,7.
Вариант № 9: 160; 130; 159; 165; 156; 141; 157; 172; 157; 145; 163; 177; 163; 150; 160; 180; 159.
Вариант № 10: 18; 17; 16; 15; 16; 14; 13; 12; 14; 13; 10; 10; 11; 10; 9; 8.
Вариант № 11: 55; 51; 50; 57; 54; 53; 59; 56; 54; 60; 58; 55.
Вариант № 12: 60,9; 60,8; 60,6; 60,4; 61,5; 65,6; 64,7; 63,8; 62,4; 67; 70,8; 68,7; 67,9; 65,2; 71,1; 74,6; 72,1; 69,4; 69,5; 72,5; 77,5; 72,8.
Вариант № 13: 10,8; 10,4; 10,3; 10,1; 11,3; 10,7; 10,5; 10,4; 12,3; 12; 11,4; 11; 13,3; 12,7; 12; 11,9.
Вариант № 14: 0,62; 0,61; 0,6; 0,63; 0,62; 0,61; 0,65; 0,64; 0,62; 0,67; 0,66; 0,65; 0,71; 0,7; 0,68.
Вариант № 15: 37,5; 37,1; 86,9; 101,5; 35,7; 47,1; 99,2; 102; 39; 35,5; 99,2; 90,5; 46,1; 45,4; 92; 92,7.
Вариант № 16: 3; 5; 6; 7; 6; 4; 6; 9; 10; 7; 5; 10; 11; 12; 9; 7; 10; 14; 12; 10; 11; 15; 13.
Вариант № 17: 8,4; 8,6; 8,8; 9,5; 8,5; 9,1; 9,2; 9,9; 9,7; 9,9; 10,1; 10,8; 10,5; 10,7; 12,2; 11,9; 12,3; 12,5; 13,2.
Вариант № 18: 15; 16; 18; 20; 17; 18; 20; 22; 19; 21; 23; 25; 20; 26; 28; 29.
Вариант № 19: 73; 75; 76; 76; 74; 73; 74; 78; 79; 77; 76; 75; 77; 80; 82; 83; 80; 79; 81; 85; 83; 81; 84.
Вариант № 20: 57; 59; 60; 58; 60; 63; 64; 62; 66; 67; 69; 68; 67; 68; 71; 69.
Вариант № 21: 13,7; 24,7; 42,7; 12,6; 13,4; 25,2; 50,1; 15,2; 14,4; 27,3; 53,6; 15,7; 15,9; 29,4; 58,8; 16,4.
Вариант № 22: 29; 27; 25; 30; 32; 33; 27; 26; 28; 32; 34; 29; 30; 33; 35; 36; 31; 30; 37; 38.
Вариант № 23: 8,3; 8,7; 10,3; 10,7; 9,9; 8,6; 8,9; 9,1; 10,9; 10,8; 10,2; 8,9; 10,2; 10,1; 11,1; 12,2; 10,4; 9,7; 9,2; 9,6; 10,8; 11,4.
Вариант № 24: 8,3; 8,7; 10,3; 10,7; 9,9; 8,6; 9,4; 9,7; 11,2; 11; 9,4; 9,3; 10,2; 10,1; 11,1; 12,2; 10,4; 9,7; 9,2; 9,6; 10,8; 11,4.
Вариант № 25: 128; 130; 132; 131; 130; 129; 129; 132; 133; 132; 131; 132; 135; 136; 135; 133; 132; 135; 137; 136; 133.
Вариант № 26: 8,9; 9,1; 10,9; 10,8; 10,2; 8,9; 9,4; 9,7; 11,2; 11; 9,4; 9,3; 10,2; 10,1; 11,1; 12,2; 10,4; 9,7; 9,2; 9,6; 10,8; 11,4.
Задание 5.3. По имеющемуся тренд–сезонному временному ряду 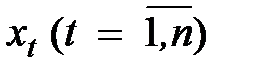получить прогнозную аддитивную и мультипликативную модели ряда и выполнить прогноз этого ряда на два временных шага. Необходимо:
1. Определить значение периода L по максимальное значение автокорреляционной функции ряда.
2. Определить значения коэффициентов сезонности.
3. Определить коэффициенты линейного тренда.
4. Выполнить прогноз этого ряда на два временных шага.
5. Оценить качество модели: вычислить коэффициент детерминации и среднюю ошибку прогноза. Исследовать адекватность полученной модели.
6. Исходным данным дать физическое толкование (интерпретацию) и проанализировать полученные результаты.
Исходные данные взять из задания 5.2.
Дата: 2019-03-05, просмотров: 381.
