Пусть заданы:
1) целевая функция предпочтения потребителя
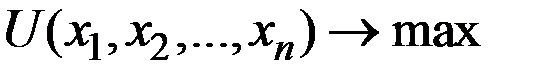
(где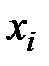 
– количество 
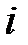–го блага);
2) вектор – столбец цен 
;
3) доход R.
Записав бюджетное ограничение и ограничения на неотрицательность переменных, получаем задачу: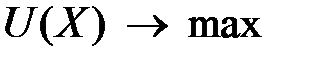 
;
при условиях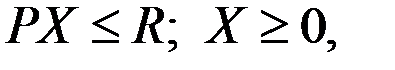 
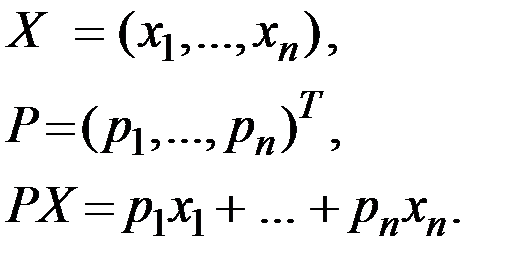
Будем, как и ранее, считать, что неотрицательность переменных обеспечивается свойствами целевой функции и бюджетного ограничения.
В этом случае можно записать функцию Лагранжа и исследовать её на безусловный экстремум.
Функция Лагранжа будет иметь матричный вид
.
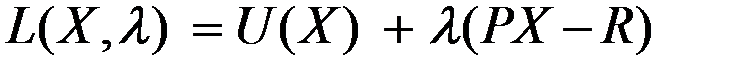Необходимые условия экстремума – равенство нулю частных производных: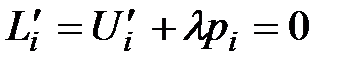 
, 
;
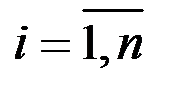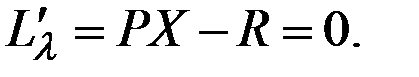
Отсюда следует, что для всех i и j в точке локального равновесия выполняется равенство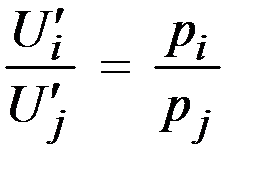 
.
Или в другой форме: 
.
Дополнительная полезность, приходящаяся на дополнительную единицу денежных затрат, в точке оптимума одинакова по всем видам благ.
Пример 6.2. Найти функции спроса в случае функции полезности
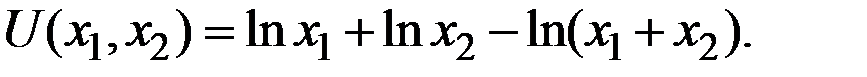
Решение. Для заданной функции полезности частные производные первого порядка таковы:
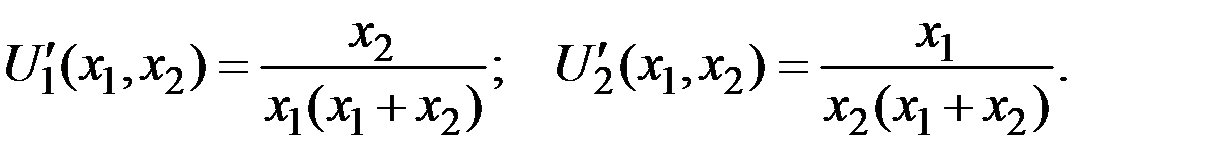
Система уравнений имеет вид
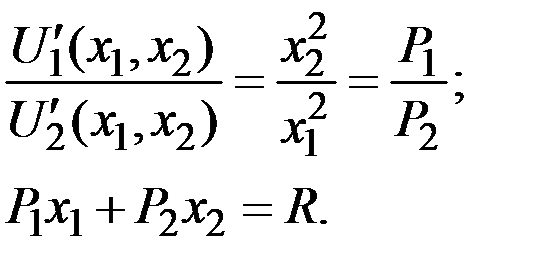
Функция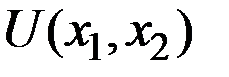 
является строго вогнутой в области 
поскольку при положительных х и у выполняются неравенства:
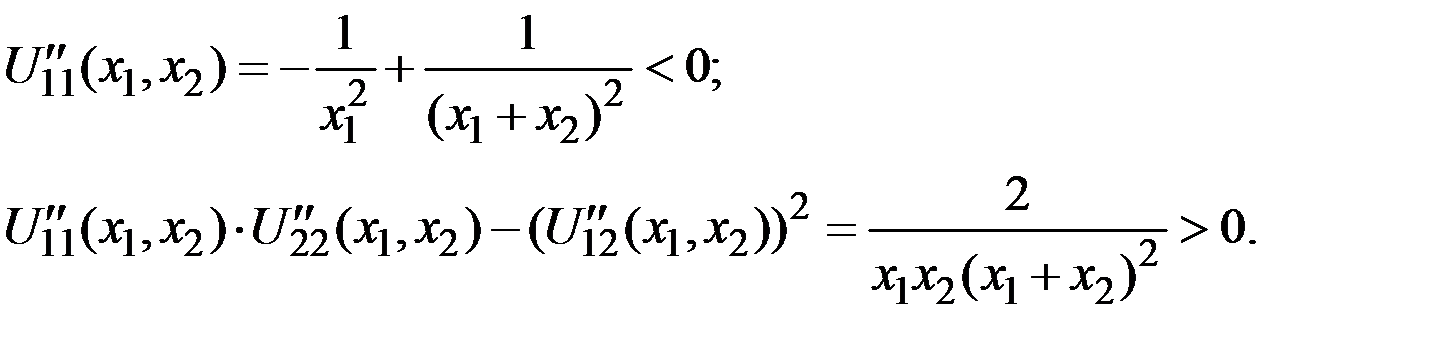
Кроме того,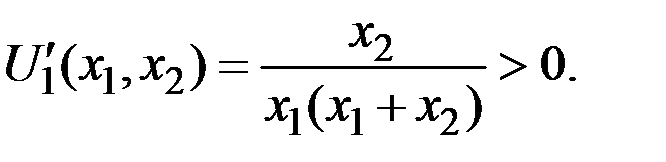 
Поэтому функции спроса таковы:
Если значение R = 100 – фиксировано, то имеем функцию спроса
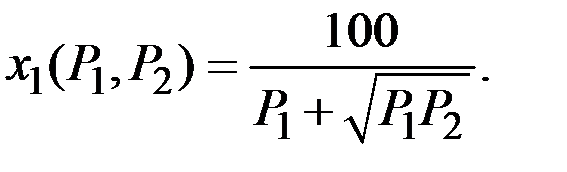
Если зафиксировать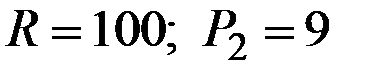 
, то получим функцию спроса вида 
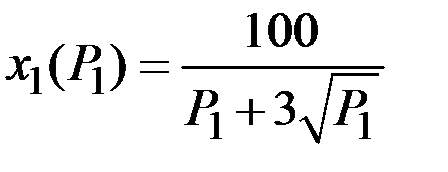и т.д.
Модель Стоуна
Получим функции спроса 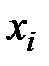на примере конкретной функции потребительского предпочтения, называемой функцией Р.Стоуна и имеющей вид:
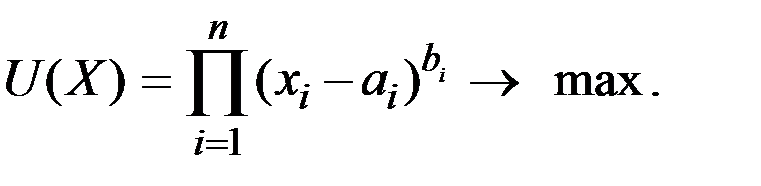
Здесь ai – минимально необходимое количество i–го блага, которое приобретается в любом случае и не является предметом выбора.
Для того чтобы набор (ai) мог быть полностью приобретён, необходимо, чтобы доход был больше количества денег, требуемого для покупки этого набора: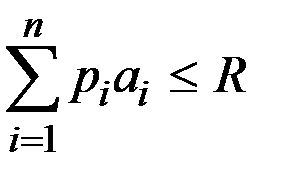 
.
Коэффициенты степени bi > 0 характеризуют «ценность» благ для потребителя.
Модель Р.Стоуна имеет вид:
;
; 
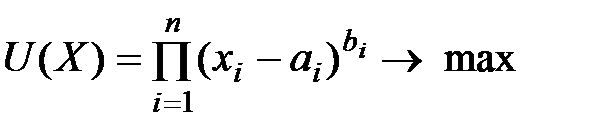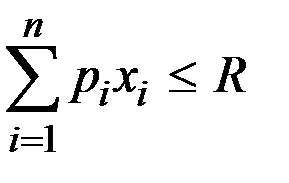Решение модели находим методом Лагранжа.
Функция Лагранжа будет иметь матричный вид
.
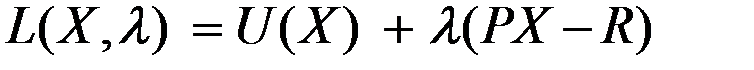Приравняв нулю частные производные функции Лагранжа по переменным х i, получаем для всех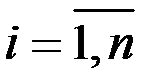 
:
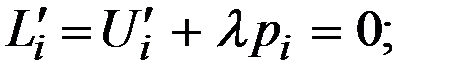
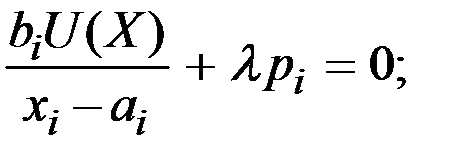
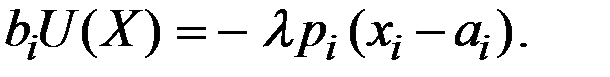
Отсюда получаем: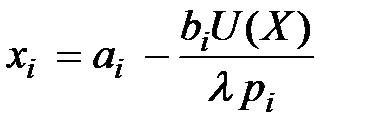 
.
К этим условиям добавляется равенство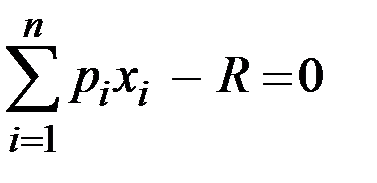 
, выполнение которого эквивалентно равенству нулю частной производной функции Лагранжа по переменной l.
Умножив каждое i–ое условие спроса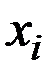 
на l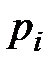 
и просуммировав их по i, получим:
.
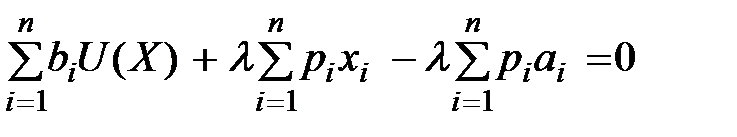Поскольку в точке оптимума бюджетное ограничение выполняется как равенство, заменим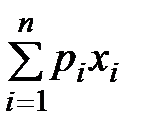 
на 
.
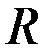Получим
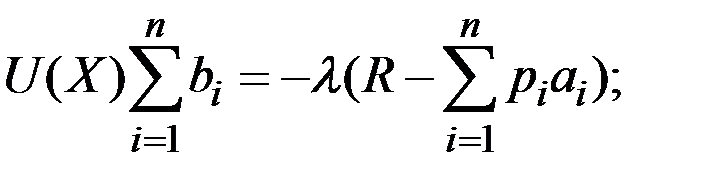
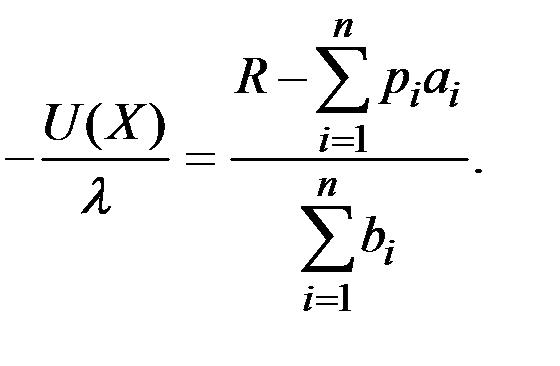
Отсюда имеем функцию спроса
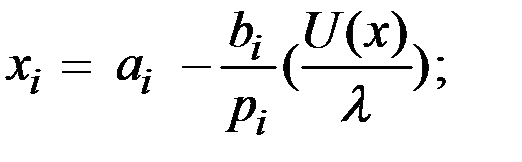
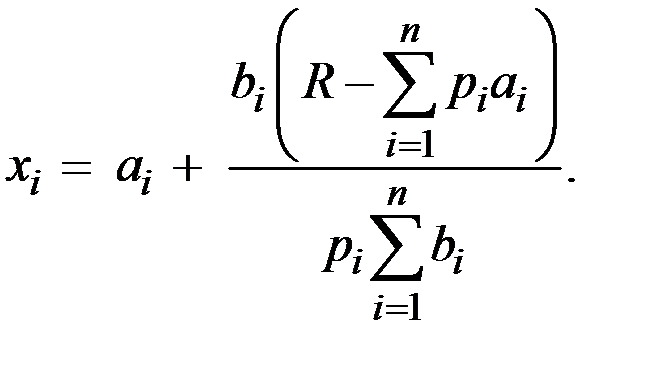
Дата: 2019-03-05, просмотров: 281.
