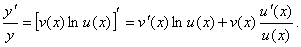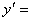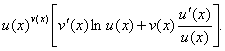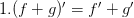
Производная суммы двух любых выражений равна сумме производных этих выражений (производная суммы равна сумме производных)
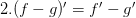
Производная разности двух любых выражений равна разности производных этих слагаемых (производная разности равна разности производных).
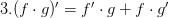
Производная от произведения двух множителей равна произведению производной первого множителя на второй плюс произведение первого множителя на производную второго (сумма поочередно взятых производных от множителей).
Комментарий репетитора по математике: когда я короткими фразами напоминаю ученику о правиле вычисления производной от произведения, я говорю так: производная первого множителя на второй плюс обмен штрихами!
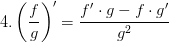
Производная от частного двух выражений равна частному разности поочередно взятых производных от множителей и квадрата знаменателя.
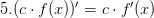
Производная от произведения числа на функцию. Чтобы найти производную от произведения числа на буквенное выражение (на функцию) нужно умножить это число на производную этого буквенного выражения.
Производная сложной функции:
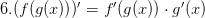
Для вычисления производной сложной функции необходимо найти производную внешней функции и умножить ее на производную внутренней функции.
| Производная сложной и обратной функций | 
| 
| 
|
Пусть функция 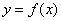 удовлетворяет условиям теоремы о непрерывности сложной функции и функция удовлетворяет условиям теоремы о непрерывности сложной функции и функция 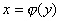 является для нее Обратной.
Теорема (о производной обратной функции)
Пусть функция является для нее Обратной.
Теорема (о производной обратной функции)
Пусть функция 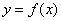 является непрерывной и строго монотонной в некоторой окрестности точки является непрерывной и строго монотонной в некоторой окрестности точки 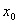 и имеет в этой точке производную и имеет в этой точке производную 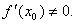 Тогда Обратная функция Тогда Обратная функция 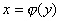 также имеет в соответствующей точке также имеет в соответствующей точке 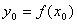 производную, причем производную, причем
Теорема (о производной сложной функции). Пусть функция
В данной теореме рассмотрена суперпозиция двух функций, где
Пример: Найти производную функции Решение Эту функцию можно представить через промежуточную переменную Производная неявной функции Пусть дифференцируемая функция Пример Найти производную функции Решение Дифференцируя обе части равенства и учитывая, что
Значение производной при Производная показательно–степенной функции (логарифмическая производная) Пусть функция
Это выражение называется логарифмической производной функции
Где
С учетом вида функции
|
Дата: 2019-03-05, просмотров: 344.
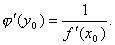
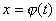 имеет производную в точке
имеет производную в точке 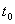 , а функция
, а функция 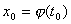 . Тогда сложная функция
. Тогда сложная функция 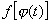 имеет Производную в точке
имеет Производную в точке 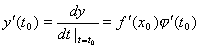
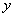 зависит от
зависит от 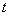 через промежуточную переменную
через промежуточную переменную 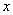 . Возможна и более сложная зависимость с несколькими промежуточными переменными, однако правило дифференцирования сложной функции остается тем же. Например, если
. Возможна и более сложная зависимость с несколькими промежуточными переменными, однако правило дифференцирования сложной функции остается тем же. Например, если 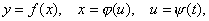 то производная
то производная 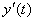 вычисляется по формуле
вычисляется по формуле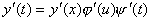
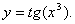
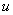 как
как 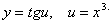 Тогда по формуле (5.3.2)
Тогда по формуле (5.3.2) 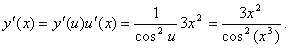
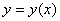 удовлетворяет уравнению
удовлетворяет уравнению 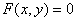 , т. е. задана неявно. Чтобы найти производную функции
, т. е. задана неявно. Чтобы найти производную функции 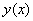 , заданную неявно, необходимо продифференцировать обе части уравнения по переменной
, заданную неявно, необходимо продифференцировать обе части уравнения по переменной 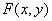 как сложную функцию от
как сложную функцию от 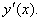
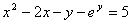 , и вычислить ее значение в точке (2;0).
, и вычислить ее значение в точке (2;0).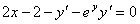 , откуда
, откуда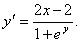
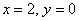 равно
равно 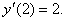
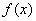 положительна и дифференцируема в точке
положительна и дифференцируема в точке 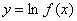 . По правилу дифференцирования сложной функции получаем
. По правилу дифференцирования сложной функции получаем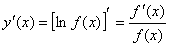 .
.
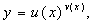
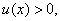 и
и 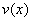 – некоторые функции от аргумента
– некоторые функции от аргумента 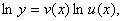 то использование формулы (5.3.5) приводит к равенству
то использование формулы (5.3.5) приводит к равенству