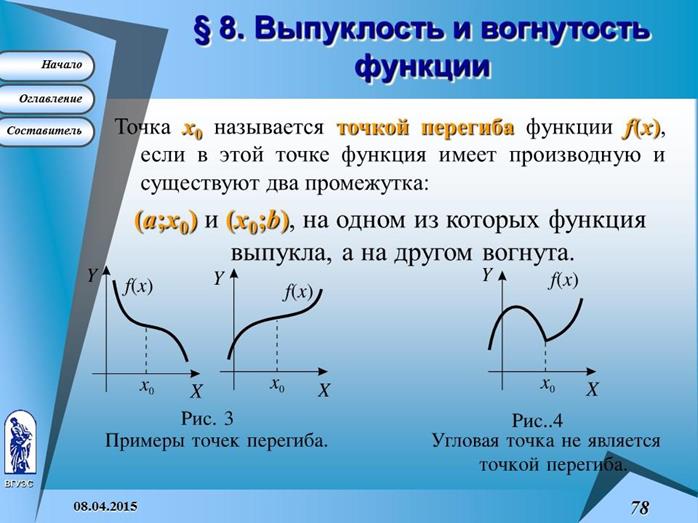
Нахождение интервалов выпуклости функции.

Сформулируем теорему, которая позволяет определять промежутки выпуклости функции.

Теорема.

Если функция y=f(x) имеет конечную вторую производную на интервале Х и если выполняется неравенство 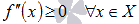( 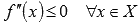), то график функции имеет выпуклость направленную вниз (вверх) на Х.

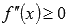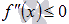Эта теорема позволяет находитьть промежутки вогнутости и выпуклости функции, нужно лишь на области определения исходной функции решить неравенства и соответственно.

Следует отметить, что точки, в которых функция y=f(x) определена, а вторая производная не существует, будем включать в интервалы вогнутости и выпуклости.

Разберемся с этим на примере.

Пример.

Выяснить промежутки, на которых график функции 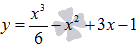имеет выпуклость направленную вверх и выпуклость направленную вниз.

Решение.

Область определения функции 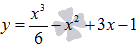- это все множество действительных чисел.

Найдем вторую производную.

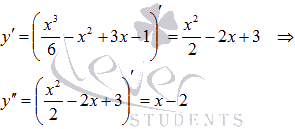
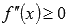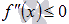Область определения второй производной совпадает с областью определения исходной функции, поэтому, чтобы выяснить интервалы вогнутости и выпуклости, достаточно решить и соответственно.

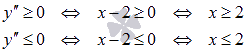
Следовательно, функция выпуклая вниз на интервале 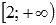и выпуклая вверх на интервале .

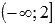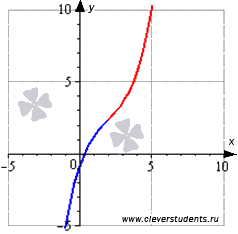
Графическая иллюстрация.

Часть графика функции на интервале выпуклости изображена синим цветом, на интервале вогнутости – красным цветом.

Сейчас рассмотрим пример, когда область определения второй производной не совпадает с областью определения функции. В этом случае, как мы уже отмечали, точки области определения, в которых не существует конечная вторая производная, следует включать в интервалы выпуклости и (или) вогнутости.

Пример.

Найти промежутки выпуклости и вогнутости графика функции .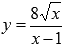

Решение.

Начнем с области определения функции:

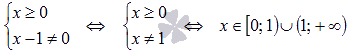
Найдем вторую производную:

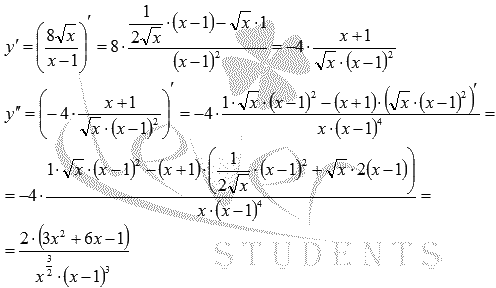
Областью определения второй производной является множество 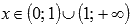. Как видите, x=0 принадлежит области определения исходной функции, но не принадлежит области определения второй производной. Не забывайте про эту точку, ее нужно будет включить в интервал выпуклости и (или) вогнутости.

Теперь решаем неравенства 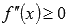и 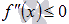на области определения исходной функции. Применим метод интервалов. Числитель выражения 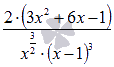обращается в ноль пр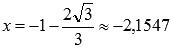и или 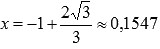, знаменатель – при x = 0 или x = 1. Схематично наносим эти точки на числовую прямую и выясняем знак выражения на каждом из интервалов, входящих в область определения исходной функции (она показана заштрихованной областью на нижней числовой прямой). При положительном значении ставим знак «плюс», при отрицательном – знак «минус».

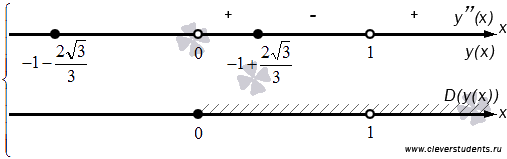
Таким образом,

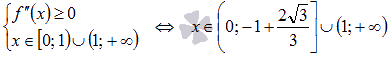
и

Следовательно, включив точку x=0, получаем ответ.

При 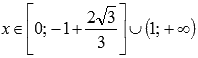график функции имеет выпуклость направленную вниз, при 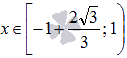- выпуклость направленную вверх.

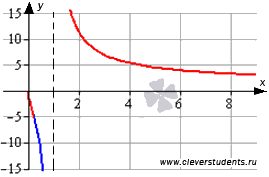
Графическая иллюстрация.

Часть графика функции на интервале выпуклости изображена синим цветом, на интервалах вогнутости – красным цветом, черной пунктирной прямой является вертикальная асимптота.

К началу страницы