Находим все абсциссы  возможных точек перегиба графика функции (
возможных точек перегиба графика функции ( 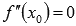 или
или 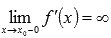 и
и  ) и выясняем, проходя через какие
) и выясняем, проходя через какие  вторая производная меняет знак. Такие значения и будут абсциссами точек перегиба, а соответствующие им точки
вторая производная меняет знак. Такие значения и будут абсциссами точек перегиба, а соответствующие им точки 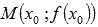 будут точками перегиба графика функции.
будут точками перегиба графика функции.
Рассмотрим два примера нахождения точек перегиба для разъяснения.
Пример.
Найти точки перегиба и интервалы выпуклости и вогнутости графика функции 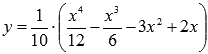 .
.
Решение.
Областью определения функции является все множество действительных чисел.
Найдем первую производную:
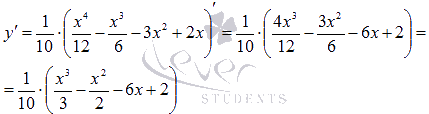
Областью определения первой производной также является все множество действительных чисел, поэтому равенства 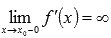 и
и  не выполняется ни для каких
не выполняется ни для каких  .
.
Найдем вторую производную:
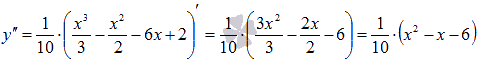
Выясним при каких значениях аргумента x вторая производная обращается в ноль:
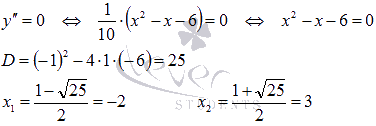
Таким образом, абсциссами возможных точек перегиба являются x=-2 и x=3.
Теперь осталось проверить по достаточному признаку перегиба, в каких из этих точек вторая производная меняет знак. Для этого нанесем точки x=-2 и x=3 на числовую ось и, как в обобщенном методе интервалов, расставим знаки второй производной над каждым промежутком. Под каждым интервалом схематично дугами показано направление выпуклости графика функции.
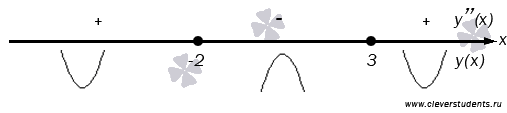
Вторая производная меняет знак с плюса на минус, проходя через точку x=-2слева направо, и меняет знак с минуса на плюс, проходя через x=3. Следовательно, и x=-2 и x=3 являются абсциссами точек перегиба графика функции. Им соответствуют точки графика 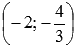 и
и 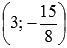 .
.
Взглянув еще раз на числовую ось и знаки второй производной на ее промежутках, можно делать вывод об интервалах выпуклости и вогнутости. График функции выпуклый на интервале 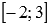 и вогнутый на интервалах
и вогнутый на интервалах 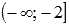 и
и 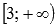 .
.
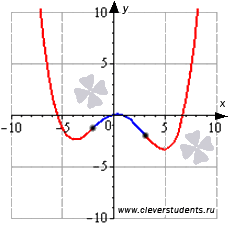
Графическая иллюстрация.
Часть графика функции на интервале выпуклости изображена синим цветом, на интервалах вогнутости – красным цветом, точки перегиба показаны черными точками.
Пример.
Найдите абсциссы всех точек перегиба графика функции 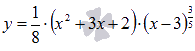 .
.
Решение.
Областью определения данной функции является все множество действительных чисел.
Найдем производную.
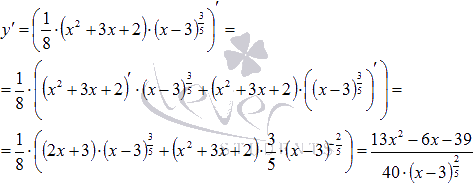
Первая производная, в отличии от исходной функции, не определена при x=3. Но 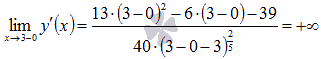 и
и 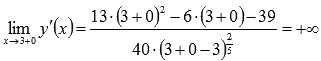 . Следовательно, в точке с абсциссой x=3существует вертикальная касательная к графику исходной функции. Таким образом, x=3 может быть абсциссой точки перегиба графика функции.
. Следовательно, в точке с абсциссой x=3существует вертикальная касательная к графику исходной функции. Таким образом, x=3 может быть абсциссой точки перегиба графика функции.
Находим вторую производную, область ее определения и точки, в которых она обращается в ноль:
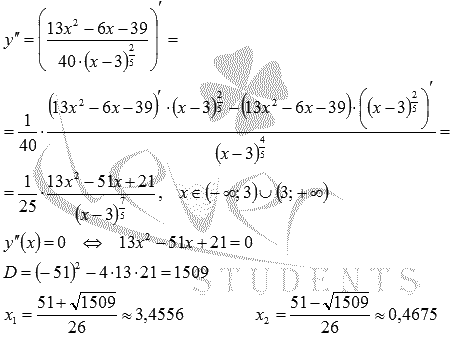
Получили еще две возможные абсциссы точек перегиба. Отмечаем все три точки на числовой прямой и определяем знак второй производной на каждом из полученных интервалов.
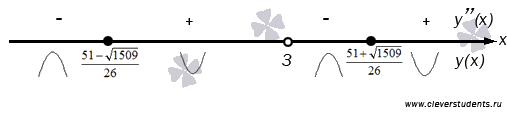
Вторая производная меняет знак, проходя через каждую из точек, следовательно, все они являются абсциссами точек перегиба.
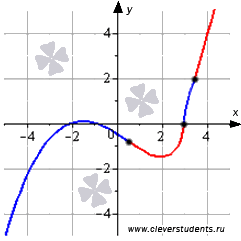
Графическая иллюстрация.
Части графика функции на интервалах выпуклости изображены синим цветом, на интервалах вогнутости – красным цветом, точки перегиба показаны черными точками.
Первое достаточное условие перегиба графика функции позволяет определять точки перегиба и не требуют существования второй производной в них. Поэтому, первое достаточное условие можно считать универсальным и самым используемым.
Сейчас сформулируем еще два достаточных условия перегиба, но они применимы лишь при существовании конечной производной в точке перегиба до некоторого порядка.
Дата: 2019-03-05, просмотров: 463.