Условия задач, в которых приходится отыскивать угол между прямой и плоскостью, достаточно разнообразны. В зависимости от исходных данных, приходится подбирать соответствующий метод решения. Часто справиться с задачей нахождения угла между прямой и плоскостью помогают признаки равенства или подобия фигур, теорема косинусов и определения синуса, косинуса и тангенса угла. Также можно найти угол между прямой и плоскостью методом координат. Остановимся на нем подробнее.
Пусть в трехмерном пространстве введена прямоугольная система координат Oxyz , в ней задана прямая a, которая пересекает плоскость 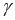 в точке M и не перпендикулярна плоскости
в точке M и не перпендикулярна плоскости 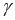 , и требуется найти угол
, и требуется найти угол 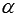 между прямой a и плоскостью
между прямой a и плоскостью 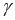 .
.
Начнем с начальных данных, от которых мы будем отталкиваться при определении угла между прямой и плоскостью методом координат.
Прямой a в заданной прямоугольной системе координат Oxyz соответствуют некоторые уравнения прямой в пространстве и направляющий вектор прямой в пространстве, а плоскости  - уравнение плоскости некоторого вида и нормальный вектор плоскости. Пусть
- уравнение плоскости некоторого вида и нормальный вектор плоскости. Пусть 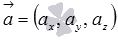 - направляющий вектор прямой a,
- направляющий вектор прямой a, 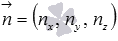 - нормальный вектор плоскости
- нормальный вектор плоскости  . Итак, будем считать, что нам известны координаты направляющего вектора прямой a и координаты нормального вектора плоскости
. Итак, будем считать, что нам известны координаты направляющего вектора прямой a и координаты нормального вектора плоскости 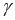 (если известны уравнения прямой a и плоскости
(если известны уравнения прямой a и плоскости 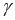 , то координаты векторов
, то координаты векторов 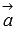 и
и 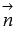 определяются по этим уравнениям).
определяются по этим уравнениям).
Осталось получить формулу, которая позволят вычислять угол между прямой и плоскостью по известным координатам направляющего вектора прямой и нормального вектора плоскости.
Отложим векторы 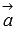 и
и 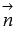 от точки пересечения прямой a и плоскости
от точки пересечения прямой a и плоскости 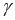 . В зависимости от координат векторов
. В зависимости от координат векторов 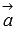 и
и 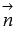 возможны четыре варианта расположения этих векторов относительно заданных прямой и плоскости. Изобразим их на чертеже.
возможны четыре варианта расположения этих векторов относительно заданных прямой и плоскости. Изобразим их на чертеже.
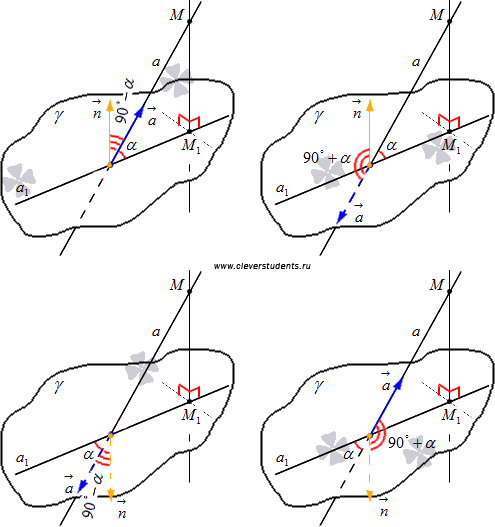
Очевидно, если угол между векторами 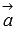 и
и 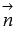 (обозначим его
(обозначим его 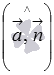 ) острый, то он дополняет искомый угол
) острый, то он дополняет искомый угол 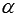 между прямой и плоскостью до прямого угла, то есть,
между прямой и плоскостью до прямого угла, то есть, 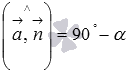 . Если же
. Если же 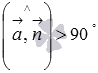 , то
, то 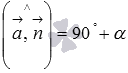 .
.
Так как косинусы равных углов равны, то последние равенства можно записать следующим образом:
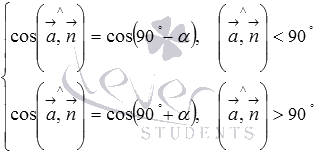
Формулы приведения приводят нас к равенствам 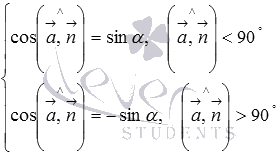 , которые после преобразований принимают вид
, которые после преобразований принимают вид
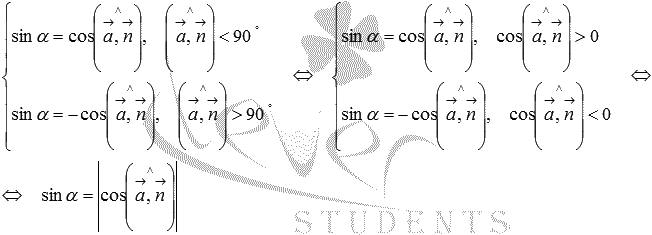
То есть, синус угла между прямой и плоскостью равен модулю косинуса угла между направляющим вектором прямой и нормальным вектором плоскости.
В разделе нахождение угла между двумя векторами мы выяснили, что угол между векторами равен отношению скалярного произведения векторов и произведения длин этих векторов, тогда для вычисления синуса угла между прямой и плоскостью справедлива формула  .
.
Следовательно, формула для вычисления угла между прямой и плоскостью по координатам направляющего вектора прямой и нормального вектора плоскости имеет вид 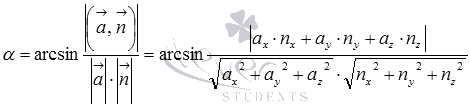 .
.
Основное тригонометрическое тождество позволяет найти косинус угла при известном синусе. Так как угол между прямой и плоскостью острый, то косинус этого угла является положительным числом и вычисляется по формуле 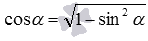 .
.
Дата: 2019-03-05, просмотров: 355.