Предел функции - основные понятия.

Бесконечность обозначают символом 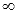. По сути, бесконечность 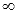это есть либо бесконечно большое положительное число 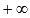, либо бесконечно большое отрицательное число .

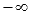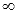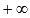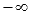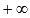Что это означает: когда Вы видите , то не имеет разницы это или . Но лучше не заменять на 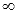, равно как и 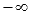лучше не заменять на .

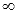Записывать предел функции f(x) принято в виде 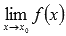, снизу указывается аргумент x и через стрелочку к какому значению 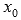он стремится.

Если 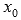представляет из себя конкретное действительное число, то говорят о пределе функции в точке.

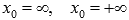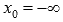Если или . то говорят о пределе функции на бесконечности.

Сам предел может быть равен конкретному действительному числу 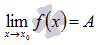, в этом случае говорят, что предел конечен.

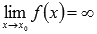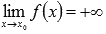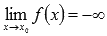Если , или , то говорят, что предел бесконечен.

Еще говорят, что предел не существует, если нельзя определить конкретное значение предела или его бесконечное значение ( 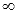, 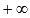или 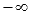). Например, предел от синуса на бесконечности не существует.

Предел функции - основные определения.

Пришло время заняться нахождением значений пределов функций на бесконечности и в точке. В этом нам помогут несколько определений. Эти определения опираются на числовые последовательности и их сходимость или расходимость.

Определение (нахождение предела функции на бесконечности).

Число А называется пределом функции f(x) при 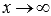, если для любой бесконечно большой последовательности аргументов функции (бесконечно большой положительной или отрицательной), последовательность значений этой функции сходится к А. Обозначается .

Замечание.

Предел функции f(x) при 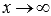бесконечен, если для любой бесконечно большой последовательности аргументов функции (бесконечно большой положительной или отрицательной), последовательность значений этой функции является бесконечно большой положительной или бесконечно большой отрицательной. Обозначается .

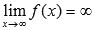Пример.

Используя определение предела при 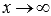доказать равенство .

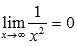Решение.

Запишем последовательность значений функции 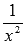для бесконечно большой положительной последовательности значений аргумента .

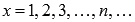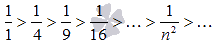
Очевидно, что члены этой последовательности монотонно убывают к нулю.

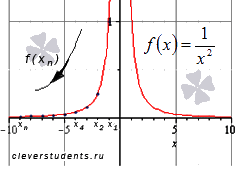
Графическая иллюстрация.

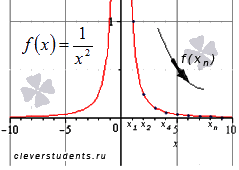
Теперь запишем последовательность значений функции 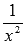для бесконечно большой отрицательной последовательности значений аргумента .

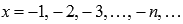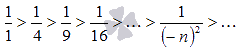
Члены этой последовательности также монотонно убывают к нулю, что доказывает исходное равенство.

Графическая иллюстрация.

Пример.

Найти предел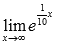

Решение.

Запишем последовательность значений функции 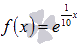для бесконечно большой положительной последовательности значений аргумента. К примеру, возьмем .

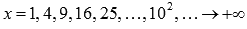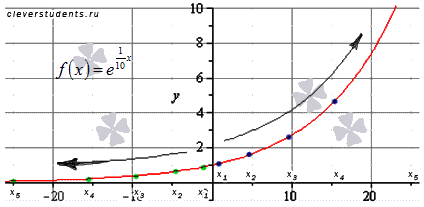
Последовательность значений функции при этом будет (синие точки на графике)

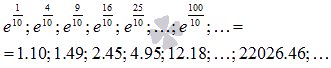
Очевидно, что эта последовательность является бесконечно большой положительной, следовательно,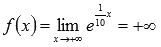

А сейчас запишем последовательность значений функции 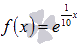для бесконечно большой отрицательной последовательности значений аргумента. К примеру, возьмем .

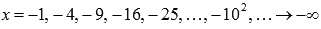Последовательность значений функции при этом будет (зеленые точки на графике)

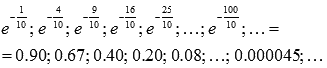
Очевидно, что эта последовательность сходится к нулю, следовательно,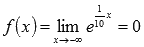

Графическая иллюстрация

Ответ:

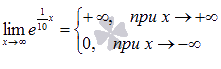
Сейчас поговорим о существовании и нахождении предела функции в точке. Все основывается на определении односторонних пределов. Без вычисления односторонних пределов не обойтись при нахождении вертикальных асимптот графика функции.

Определение (нахождение предела функции слева).

Число В называется пределом функции f(x) слева при 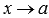, если для любой сходящейся к а последовательности аргументов функции 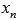, значения которых остаются меньше а ( 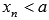), последовательность значений этой функции сходится к В.

Обозначается .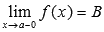

Определение (нахождение предела функции справа).

Число В называется пределом функции f(x) справа при 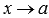, если для любой сходящейся к а последовательности аргументов функции 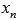, значения которых остаются больше а ( 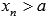), последовательность значений этой функции сходится к В.

Обозначается .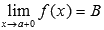

Определение (существование предела функции в точке).

Предел функции f(x) в точке а существует, если существуют пределы слева и справа а и они равны между собой.

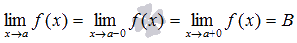
Замечание.

Предел функции f(x) в точке а бесконечен, если пределы слева и справа абесконечны.

Поясним эти определения на примере.

Пример.

Доказать существование конечного предела функции 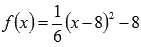в точке 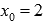. Найти его значение.

Решение.

Будем отталкиваться от определения существования предела функции в точке.

Во-первых, покажем существование предела слева. Для этого возьмем последовательность аргументов 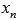, сходящуюся к 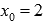, причем 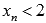. Примером такой последовательности может являться

Соответствующая последовательность значений функции будет иметь вид

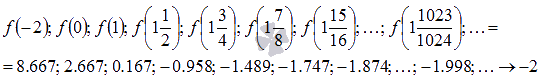
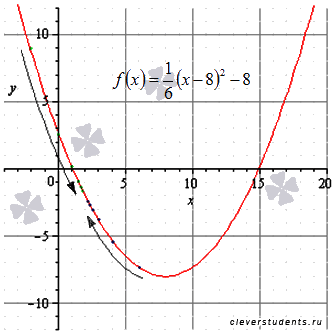
На рисунке соответствующие значения показаны зелеными точками.

Легко видеть, что эта последовательность сходится к -2, поэтому .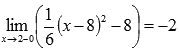

Во-вторых, покажем существование предела справа. Для этого возьмем последовательность аргументов 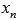, сходящуюся к 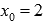, причем 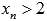. Примером такой последовательности может являться

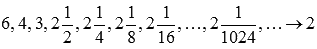
Соответствующая последовательность значений функции будет иметь вид

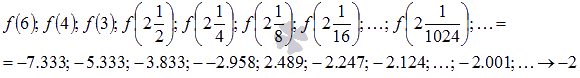
На рисунке соответствующие значения показаны синими точками.

Легко видеть, что эта последовательность также сходится к -2, поэтому .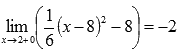

Этим мы показали, что пределы слева и справа равны, следовательно, по определению существует предел функции 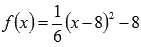в точке 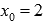, причем

Графическая иллюстрация.