Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

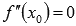Если , а 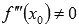, тогда является абсциссой точки перегиба графика функции y=f(x).

Пример.

Выяснить, является ли точка 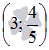точкой перегиба графика функции .

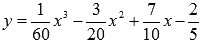Решение.

Для начала убедимся, что точка 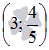принадлежит графику функции:

Функция определена для всех действительных значений аргумента. Найдем первую и вторую производные.

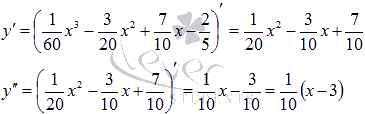
Вторая производная обращается в ноль при x=3, то есть необходимое условие перегиба графика функции в точке 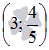выполнено, и эта точка может быть точкой перегиба. Воспользуемся вторым достаточным условием перегиба. Для этого найдем третью производную и убедимся, что ее значение при x=3отлично от нуля.

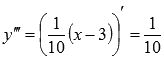
Очевидно, что значение третьей производной отлично от нуля для любых x, в том числе и для x=3. Поэтому, по второму достаточному условию перегиба графика функции, точка 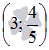является точкой перегиба.

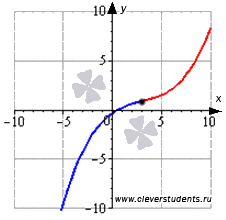
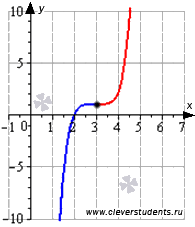
Графическая иллюстрация.

Часть графика функции на интервале выпуклости изображена синим цветом, на интервале вогнутости – красным цветом, точка перегиба показана черной точкой.

Третье достаточное условие перегиба.

Пусть 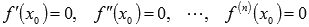, а 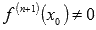, тогда если n – четное число, то является абсциссой точки перегиба графика функции y=f(x).

Пример.

Найдите точки перегиба графика функции .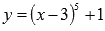

Решение.

Функция определена на всем множестве действительных чисел.

Найдем ее производную: 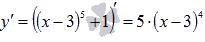. Очевидно, что она также определена для всех действительных x, поэтому, в любой из точек ее графика существует невертикальная касательная.

Определим значения х, при которых вторая производная обращается в ноль.

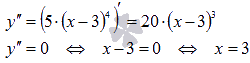
Таким образом, в точке с абсциссой x=3 может быть перегиб графика функции. Чтобы убедиться в том, что х=3 действительно абсцисса точки перегиба, воспользуемся третьим достаточным условием.

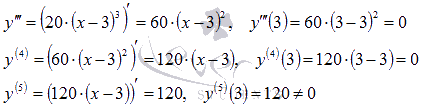
По третьему достаточному условию перегиба графика функции имеем n=4(пятая производная обращается в ноль) – четное, поэтому x=3 является абсциссой точки перегиба и ей соответствует точка графика функции (3;1).

Графическая иллюстрация.

Часть графика функции на интервале выпуклости изображена синим цветом, на интервале вогнутости – красным цветом, точка перегиба показана черной точкой.

 

 

Асимптоты кривой

Прямая называется асимптотой кривой y = f (x), если расстояние от точки М кривой до этой прямой стремится к нулю при удалении точки М вдоль кривой в бесконечность от начала координат (рис. 1.7).

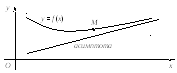
Рис. 1.7

Различают вертикальные и наклонные асимптоты. Вертикальная асимптота имеет уравнение вида x = x₀ и является прямой, параллельной оси Оy. Наклонная асимптота имеет уравнение вида y = k x + b. В частном случае при k = 0 асимптота называется горизонтальной, так как ее уравнение y = bесть прямая, параллельная оси Ох.

В ертикальные асимптоты.

Пусть дана кривая y = f (x). Для нахождения вертикальной асимптоты этой кривой находят точки ее бесконечного разрыва (точки разрыва второго рода).

Если, например,

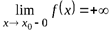и ,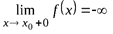

то прямая x = x₀ ─ вертикальная асимптота кривой y = f (x) (рис. 1.8).

Наклонные и горизонтальные асимптоты.

Пусть задана кривая y = f (x). Для нахождения наклонной асимптоты, уравнение которой y = k x + b, находят коэффициенты k и b, вычисляя пределы: 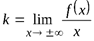, 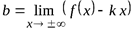. Эти пределы вычисляются отдельно для случаев 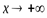и 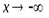. Если хотя бы один из пределов для вычисленияk и bравен ∞ или не существует, то кривая наклонных и горизонтальных асимптот не имеет.

В частном случае, когда k = 0, а b ─ конечное число, кривая имеет горизонтальную асимптоту, уравнение которой y = b.

Пример. Найти асимптоты кривой .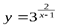

Решение. Функция 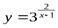определена на всем множестве действительных чиселR, кроме точки x = 1. Определим характер разрыва, для чего вычислим пределы функции при x → 1 слева (x < 1) и справа (x > 1):

, .

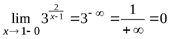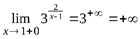Так как один из пределов бесконечен, то x = 1 является точкой разрыва второго рода, и, следовательно, кривая имеет вертикальную асимптоту x = 1.

Определим, имеет ли кривая наклонную или горизонтальную асимптоту. Для этого вычисляем соответствующие пределы:

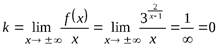
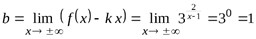, Уравнение асимптотыy = k x + b принимает вид y = 1 (горизонтальная асимптота).

С

Рис. 1.9

хематический график функции представлен на рис. 1.9.

1.14. Схема полного исследования функции и построение ее графика

Литература: [3], гл. V, § 11

[5], Ч.1, гл. 6, § 6.6

1. Находим область определения функции.

2. Устанавливаем четность, нечетность функции, периодичность. Находим характерные точки, например, точки пересечения с осями координат.

3.Находим точки разрыва функции, определяем их характер. При наличии точек разрыва второго рода (точек бесконечного разрыва) устанавливаем наличие вертикальных асимптот графика функции.

4. Находим производную функции, критические точки, промежутки монотонности, точки экстремума и значения функции в этих точках.

5. Находим вторую производную функции, интервалы выпуклости и вогнутости кривой и точки перегиба графика функции.

6.Устанавливаем наличие у исследуемой кривой наклонных и горизонтальных асимптот.

7. По полученным данным строим график функции.

Замечание. Если функция является четной или нечетной, то исследование проводят не на всей числовой оси, а на промежутке [0, +∞). Затем график продолжают симметрично относительно оси ординат на промежуток (-∞, 0), если функция четная, и относительно центра системы координат, если функция нечетная.

Если функция периодическая, то ее график строят для одного периода, а затем периодически продолжают на всю числовую ось.

Пример. Провести полное исследование функции 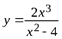и построить ее график.

Решение.

1. Функция определена и непрерывна на всей числовой оси, кроме точек x = ± 2.

2. Функция нечетная, так как для нее выполняется условие 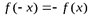. Поэтому достаточно провести исследование на промежутке [0, +∞).

3. В промежутке [0, +∞) имеется одна точка разрыва x = 2. Исследуем характер точки разрыва, для чего вычислим следующие пределы:

,

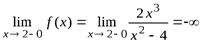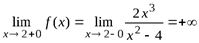
Так как односторонние пределы бесконечные, то прямая x = 2 является вертикальной асимптотой.

4. Находим первую производную:

.

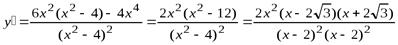Находим критические точки на промежутке [0, +∞): 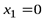, 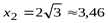. В точке 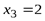производная не существует, но эта точка не является критической, так как функция в ней не определена.

5. Находим вторую производную:

.

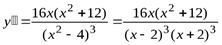Вторая производная на промежутке [0, +∞) обращается в ноль в точке x₁ = 0 и не существует в точке x₃ = 2, которая не входит в область определения функции.

По полученным данным строим таблицу:

x	0	(0, 2)	2	(2, )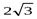
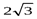
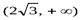
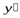
	0	−	Не существует	–	0	+
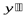
	0	−	Не существует	+	+	+
y	0		Не существует		min

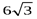
В первой строке таблицы указаны интервалы, на которые критические точки и точки, где вторая производная равна нулю или не существует, разбивают промежуток [0, +∞). Во второй строке указан знак первой производной в этих интервалах, в третьей − знак второй производной. В четвертой строке условно изображено возрастание или убывание функции на промежутке (по знаку первой производной), и выпуклость или вогнутость кривой (по знаку второй производной).

6. Ищем наклонную асимптоту:

,

.

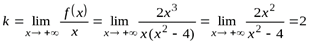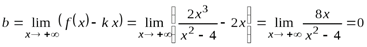Кривая на промежутке [0, +∞) имеет наклонную асимптоту .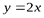

Строим вертикальную x = 2 и наклонную y = 2x асимптоты, а затем по данным таблицы строим график исследуемой функции на промежутке [0, +∞), который затем продолжаем на промежуток (-∞, 0) симметрично относительно центра системы координат.

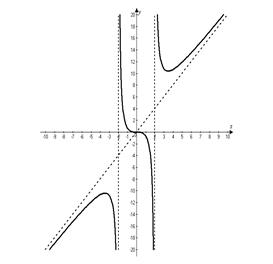
15. понятие первообразной и неопределенного интеграла таблица неопределенных интегралов

Определение первообразной.

Первообразной функции f(x) на промежутке (a; b) называется такая функция F(x), что выполняется равенство 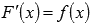для любого х из заданного промежутка.

Если принять во внимание тот факт, что производная от константы С равна нулю, то справедливо равенство 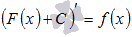. Таким образом, функция f(x) имеет множество первообразных F(x)+C, для произвольной константы С, причем эти первообразные отличаются друг от друга на произвольную постоянную величину.