Непрерывная функция — функция, которая меняется без «скачков», то есть такая, у которой малые изменения аргумента приводят к малым изменениям значения функции. График непрерывной функции является непрерывной линией.

Непрерывность функции в точке, разрывы первого и второго рода.

Исследование функции на непрерывность связано с нахождением односторонних пределов функции. Так что рекомендуем ознакомится с разделом Предел функции, основные определения и понятия, прежде чем двигаться дальше.

Определение непрерывности функции в точке.

Функция f(x) называется непрерывной в точке 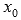, если предел слева равен пределу справа и совпадает со значением функции в точке 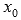, то есть .

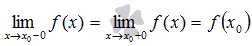Следствие.

ЗНАЧЕНИЕ ПРЕДЕЛА ФУНКЦИИ В ТОЧКАХ НЕПРЕРЫВНОСТИ СОВПАДАЕТ СО ЗНАЧЕНИЕМ ФУНКЦИИ В ЭТИХ ТОЧКАХ.

Пример.

Доказать непрерывность функции 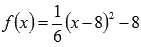в точке .

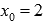Решение.

Во-первых, покажем существование предела слева. Для этого возьмем последовательность аргументов 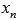, сходящуюся к 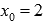, причем 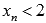. Примером такой последовательности может являться

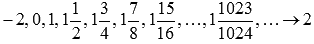
Соответствующая последовательность значений функции будет иметь вид

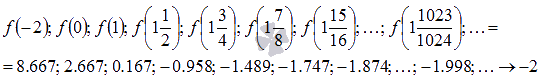
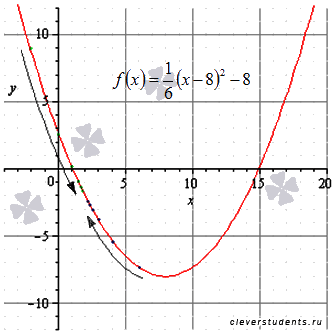
На рисунке соответствующие значения показаны зелеными точками.

Легко видеть, что эта последовательность сходится к -2, поэтому .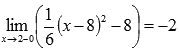

Во-вторых, покажем существование предела справа. Для этого возьмем последовательность аргументов 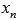, сходящуюся к 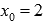, причем 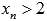. Примером такой последовательности может являться

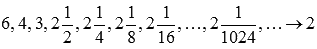
Соответствующая последовательность значений функции будет иметь вид

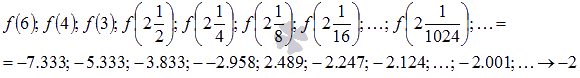
На рисунке соответствующие значения показаны синими точками.

Легко видеть, что эта последовательность также сходится к -2, поэтому .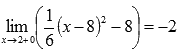

Этим мы показали, что пределы слева и справа равны, следовательно, существует предел функции 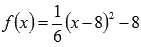в точке 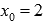, причем

Вычислив значение функции в точке 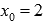можно говорить о выполнении равенства 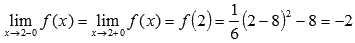, это доказывает непрерывность исходной функции в точке.

Графическая иллюстрация.

Определение устранимого разрыва первого рода.

В точке 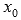функция имеет устранимый разрыв первого рода, если предел слева равен пределу справа, но они не равны значению функции в точке ,то есть .

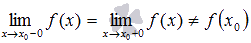Пример.

Найти точки разрыва функции и определить их тип .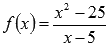

Решение.

Находим область определения функции:

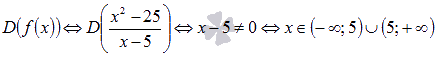
Точкой разрыва нашей функции может быть только граничная точка области определения, то есть 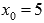. Проверим функцию на непрерывность в этой точке.

На области определения выражение 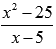можно упростить:

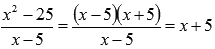
Находим пределы слева и справа. Так как функция 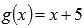непрерывна при любом действительном х, то

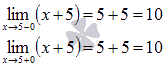
Следовательно, пределы слева и справа равны, а сама функция 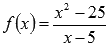в точке 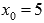не определена, поэтому, в точке 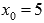функция имеет устранимый разрыв первого рода.

Определение неустранимого разрыва первого рода (точка скачка функции).

В точке 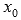функция имеет неустранимый разрыв первого рода, если пределы слева и справа НЕ равны, то есть 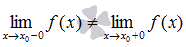. Точку 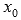в этом случае называют точкой скачка функции.

Пример.

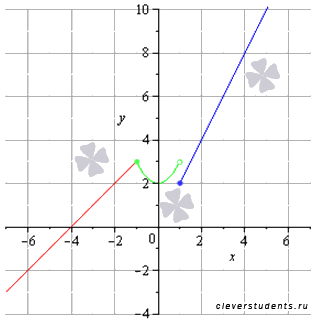
Исследовать кусочно-непрерывную функцию 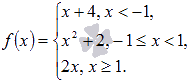на непрерывность, определить вид точек разрыва, сделать чертеж.

Решение.

Разрывы могут быть лишь в точках 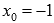или .

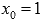Найдем пределы слева и справа от этих точек, а также значения исходной функции в этих точках.

Слева от точки 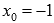наша функция есть 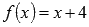и в силу непрерывности линейной функции .

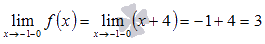В самой точке 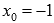наша функция есть 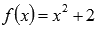, поэтому .

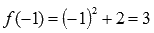На промежутке 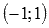наша функция есть 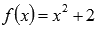и в силу непрерывности квадратичной функции

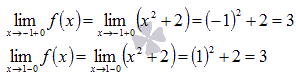
В точке 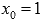наша функция есть 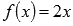, поэтому .

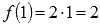Справа от 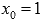наша функция есть 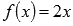и в силу непрерывности линейной функции

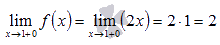
В итоге имеем:

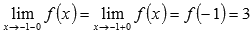· следовательно, в точке 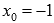исходная кусочная функция непрерывна,

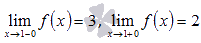· , то есть 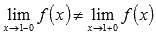, следовательно, в точке 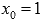неустранимый разрыв первого рода (скачок).

Графическая иллюстрация.

Определение разрыва второго рода (бесконечный разрыв).

В точке 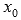функция имеет разрыв второго рода, если либо предел слева 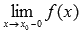, либо предел справа 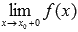, не существует или бесконечен.

Пример.

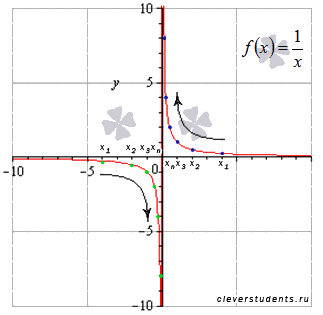
Исследовать функцию 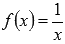на непрерывность, определить вид точек разрыва, сделать чертеж.

Решение.

Областю определения функции является интервал .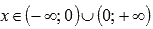

Найдем пределы функции слева и справа от точки .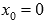

Рассмотрим произвольную последовательность значений аргумента, сходящуюся к 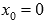слева. Например, 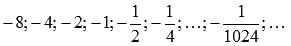и соответствующую ей последовательность значений функции

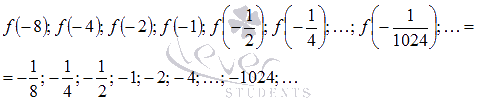
Легко показать, что эта последовательность бесконечно большая отрицательная, поэтому, .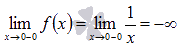

Рассмотрим произвольную последовательность значений аргумента, сходящуюся к 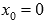справа. Например, 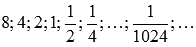и соответствующую ей последовательность значений функции

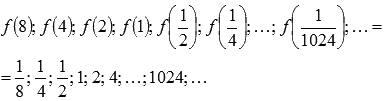
Легко показать, что эта последовательность бесконечно большая положительная, поэтому, .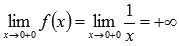

Следовательно, в точке 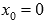функция имеет разрыв второго рода.

Графическая иллюстрация.