Сумма векторов определяется единственным способом 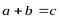(и только 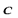). Обратная же операция – разложение вектора на несколько составляющих, неоднозначна: 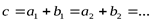. Для того, что бы сделать её однозначной, необходимо указать направления, по которым происходит разложение рассматриваемого вектора, или, как говорят, необходимо указать базис.

• Базисом в пространстве называют совокупность любых трёх некомпланарных векторов, взятых в определённом порядке .
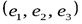• Базис на плоскости- совокупность любых двух неколлинеарных векторов, взятых в определённом порядке .
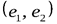• Базис на прямой– любой ненулевой вектор на этой прямой.

При определении базиса существенным является требование некомпланарности и неколлинеарности векторов. Чтобы понять смысл этого требования, необходимо рассмотреть понятие линейной зависимости и линейной независимости векторов.

Произвольное выражение вида: 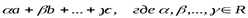, называют линейной комбинацией векторов .

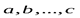Линейная комбинация нескольких векторов называется тривиальной, если все её коэффициенты равны нулю.

Векторы 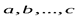называются линейно зависимыми, если существует нетривиальная линейная комбинация этих векторов равная нулю: 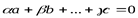(1), при условии 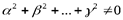. Если равенство (1) имеет место только при всех 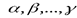одновременно равных нулю, то ненулевые векторы 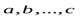будут линейно независимыми.

Легко доказать: любые два коллинеарных вектора линейно зависимы, а два неколлинеарных вектора линейно независимы.

Доказательство начнём с первого утверждения.

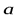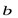Пусть векторы и коллинеарны. Покажем, что они линейно зависимы. Действительно, если они коллинеарны, то они отличаются друг от друга только на числовой множитель, т.е. 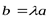, следовательно 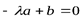. Поскольку полученная линейная комбинация явно нетривиальная и равна «0», то векторы 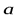и 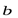линейно зависимы.

Рассмотрим теперь два неколлинеарных векторы 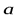и 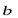. Докажем, что они линейно независимы. Доказательство построим от противного.

Предположим, что они линейно зависимы. Тогда должна существовать нетривиальная линейная комбинация 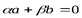. Предположим, что 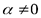, тогда 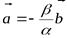. Полученное равенство означает, что векторы 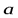и 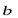коллинеарны вопреки нашему исходному предположению.

Аналогично можно доказать: любые три компланарных вектора линейно зависимы, а два некомпланарных вектора линейно независимы.

Возвращаясь к понятию базиса и к задаче разложения вектора в определённом базисе, можно сказать, что базис на плоскости и в пространстве образуется из совокупности линейно независимых векторов. Такое понятие базиса является общим, т.к. оно применимо к пространству любого числа измерений.

Выражение вида: 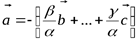, называется разложением вектора 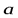по векторам ,…, .

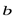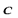Если мы будем рассматривать базис в трехмерном пространстве, то разложение вектора 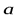по базису 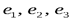будет 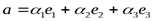, где 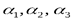-координаты вектора .

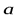В задаче разложения произвольного вектора в некотором базисе весьма важным является следующее утверждение: любой вектор 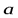может быть единственным образом разложен в данном базисе 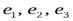.Иными словами, координаты 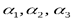для любого вектора 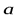относительно базиса 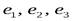определяется однозначно.

Введение базиса в пространстве и на плоскости позволяет поставить в соответствие каждому вектору 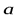упорядоченную тройку (пару) чисел – его координаты. Этот очень важный результат, позволяющий установить связь между геометрическими объектами и числами, делает возможным аналитически описывать и исследовать положение и движение физических объектов.

Совокупность точки и базиса называют системой координат.

Если векторы, образующие базис единичны и попарно перпендикулярны, то система координат называется прямоугольной, а базис ортонормированным.