Две плоскости относительно друг друга могут располагаться следующим образом:

1) быть параллельными между собой;

2) пересекаться.

Параллельные плоскости

       Если две пересекающиеся прямые одной плоскости параллельны двум пересекающимся прямым другой плоскости, то эти плоскости параллельны между собой.

Рис. 43 Плоскости, параллельные между собой

Например,  плоскость задана треугольником АВС. Через точку М провести плоскость β,  параллельную заданной. Через заданную точку М проведем две пересекающиеся прямые (рис.43), которые определяют собой искомую плоскость β, параллельные сторонам треугольника АВС:  MN║АВ, МК║ВС.

Если два пересекающихся между собой следа одной плоскости параллельны двум пересекающимся следам другой плоскости, то эти плоскости параллельны (рис.44).

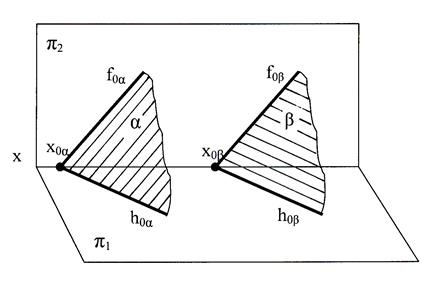
Рис. 44 Параллельные плоскости общего положения,

 заданные следами

Как построить на эпюре плоскость параллельную заданной (следами) через конкретную заданную точку? Рассмотрим эту задачу на следующем примере (рис. 45). Заданная плоскость альфа является плоскостью общего положения. Через точку А построим плоскость β , параллельную  α . Для этого через точку А проведем горизонталь будущей плоскости ( через фронтальную проекцию точки A” проведем фронтальную проекцию горизонтали  h" параллельно оси  х, а через горизонтальную А' – горизонтальную проекцию горизонтали h' параллельно горизонтальному следу заданной плоскости альфа h_{0 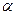.} Затем найдем фронтальный след построенной горизонтали F_h. Через F_h проведем фронтальный след искомой плоскости f_0β параллельно фронтальному следу заданной f_{0 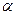.} В точке пересечения его с осью х будет находиться точка схода следов плоскости β точка x _ob. Через точку схода проведем горизонтальный след плоскости бэтта h _oβ параллельно горизонтальному следу плоскости альфа h_{0 .}                

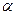Таким  образом плоскости α и β параллельны , так как их одноименные следы параллельны между собой, и плоскость β проходит через точку  А, так как точка А принадлежит горизонтали плоскости.  А как известно, точка принадлежит плоскости, если она лежит на прямой, принадлежащей этой плоскости (в нашем случае эта прямая – горизонталь).

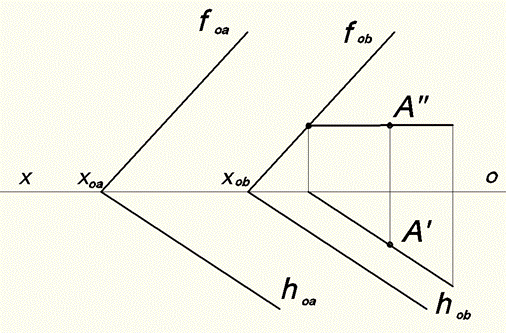
Рис. 45.Эпюр параллельных плоскостей общего положения, заданных следами.

Если параллельны не пересекающиеся следы плоскостей, то судить об их взаимном положении без дополнительного построения мы не можем. Например,  на рисунке 46 приведены профильно-проецирующие плоскости β и α, у которых фронтальные следы параллельны между собой

 f₀ 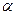║ f_0β, и горизонтальные следы  тоже - h₀ 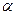║ h _oβ. Для того, чтобы определить их взаимное положение, необходимо построить  профильные следы заданных плоскостей  и по их  положению определить взаимное положение плоскостей. Так. На рисунке 46 а) плоскости β и α параллельны между собой, а на рисунке 46 б) они пересекаются

а)                                                               б)

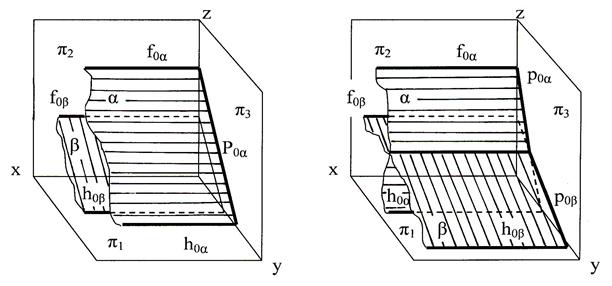
Рис. 46 Профильно-проецирующие плоскости:

а) параллельные; б) пересекающиеся

Пересекающиеся плоскости

Если хотя бы одна пара следов пересекается, то плоскости пересекаются.

Линия пересечения двух плоскостей вполне определяется двумя точками, каждая из которых принадлежит обеим плоскостям (рис.47).  MN – линия пересечения плоскостей общего положения α и β, где точки  М и N являются следами линии пересечения.

Если одна из плоскостей проецирующая (в данном случае плоскость α – горизонтально-проецирующая), то линия пересечения очевидна – это линия 1-2 (рис.48).

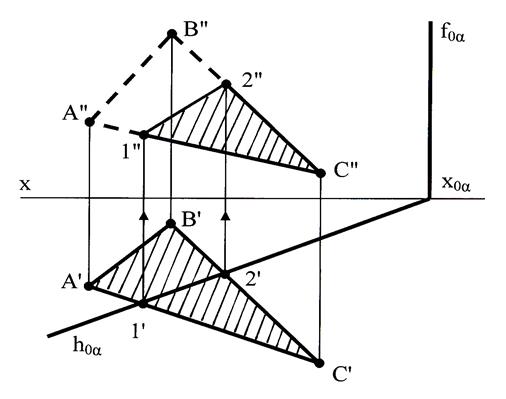
Рис.48 Пересечение треугольника горизонтально-проецирующей плоскостью

Если одна из плоскостей (плоскость β) параллельна плоскости 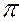₁ (рис.49),  т.е. горизонтальная,  а вторая  - плоскость общего положения (плоскость α), то линией их пересечения будет горизонталь МN.

а)                                                         б)

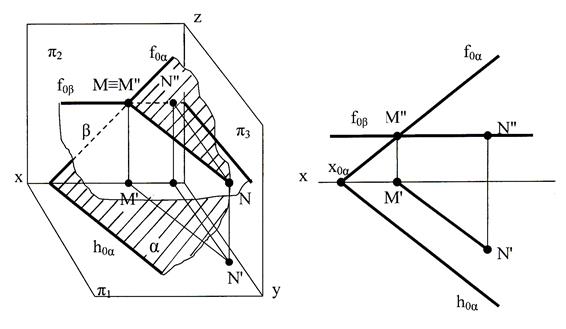
Рис. 49 Пересечение плоскости общего положения с горизонтальной плоскостью: а) в аксонометрической проекции; б) на эпюре

Теперь рассмотрим случай построения линии пересечения двух плоскостей, когда одна из плоскостей α задана следами, а другая β – треугольником АВС. Построение показано на рис.50. Для определения положения линии пересечения К₁  и К₂  заданных плоскостей возьмём две вспомогательные горизонтальные плоскости (γ₁ и γ₂), пересекающие каждую из плоскостей α и β. При пересечении заданных плоскостей плоскостью γ₁ получаем прямые с проекциями А'1', А"1", и h₁' , h₁^".

Эти прямые, расположенные в плоскости γ₁, в своём пересечении определяют первую точку К₁ линии пересечения плоскостей α и β.

Введя далее плоскость γ₂ , получаем в её пересечении с плоскостями α и β прямые с проекциями 2^'3', 2"3" и h₂', h₂". Эти прямые, расположенные в плоскости γ₂, в своём пересечении определяют вторую точку К₂, общую для α и β. Таким образом определена линия пересечения (К₁^'К₂^' – её горизонтальная проекция, К₁^"К₂^" – её фронтальная проекция) заданных плоскостей α и β.

Рис. 50 Построение линии пересечения плоскостей

Построение линии пересечения двух плоскостей по точкам пересечения прямых линий с плоскостью приведено на рис. 51. В качестве плоскостей фигурируют треугольники АВС и DEF.

Прямая К₁К₂ построена по точкам пересечения сторон АС и ВС треугольника АВС с плоскостью треугольника DEF. Вспомогательная фронтально-проецирующая плоскость α, проведённая через АС, пересекает треугольник DEF по прямой с проекциями 1"2" и 1'2'. В пересечении проекций 1'2' и А'С' получена горизонтальная проекция К₁^'. Затем построена К₁^". Аналогичным образом, используя вспомогательную

Рис. 51 Пересечение треугольников

фронтально-проецирующую плоскость β, найдены проекции точки К₂^', К₂^". Видимость треугольников определена методом конкурирующих точек.