Поскольку мы живём в трёхмерном пространстве, и на практике выполнение технических чертежей требует не два, а большее число изображений, введём в систему 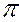 1 и
1 и 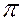 2 ещё одну плоскость проекций
2 ещё одну плоскость проекций 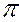 3, которая перпендикулярна к
3, которая перпендикулярна к 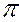 1 и к
1 и к 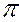 2. Её называют профильной плоскостью проекций. Помимо оси ОХ появляются оси ОY┴
2. Её называют профильной плоскостью проекций. Помимо оси ОХ появляются оси ОY┴ 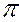 2 и ОZ┴
2 и ОZ┴ 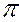 1.
1.
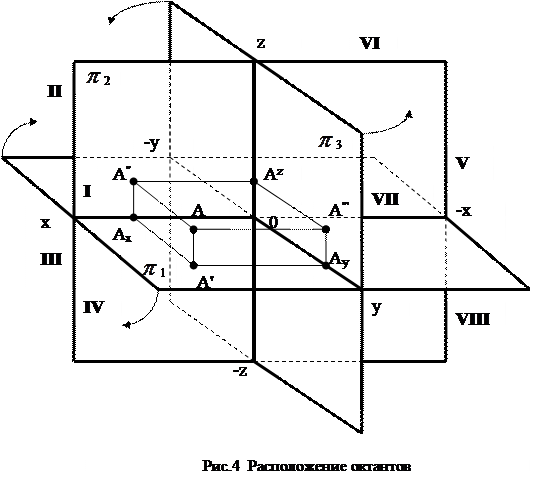 |
Три взаимно перпендикулярные пересекающиеся плоскости образуют восемь трёхгранных углов, называемых октантами и обозначаемых римскими цифрами (Рис.4). Используя систему знаков, приведённую на этом рисунке, получим таблицу:
| Октант | Х | Y | Z |
| I | + | + | + |
| II | + | − | + |
| III | + | − | − |
| IV | + | + | − |
| V | − | + | + |
| VI | − | − | + |
| VII | − | − | − |
| VIII | − | + | − |
Поворачивая плоскость 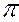 3 вокруг оси ZO (−Z) до совмещения с плоскостью
3 вокруг оси ZO (−Z) до совмещения с плоскостью 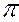 2 в направлении, указанном на рис.4, получим плоский чертеж (эпюр Монжа, рис.5) для системы трёх плоскостей проекций (вращение плоскости
2 в направлении, указанном на рис.4, получим плоский чертеж (эпюр Монжа, рис.5) для системы трёх плоскостей проекций (вращение плоскости 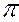 2 см. выше).
2 см. выше).


Как видно из рис.5, положение точек определяется следующими координатами (с учётом знаков):
А'(х,у), А"(х, z), А"'(у, z)
2. Проекции отрезка прямой линии. Прямые общего
и частного положения
Из геометрии известно, что однозначно положение прямой в пространстве определяют две точки. Предположим, что даны горизонтальные, фронтальные и профильные проекции точек А и В. Проведя через них одноименные проекции линии, получим горизонтальную А'В', фронтальную А"В" и профильную А"'В"' проекции прямой АВ (рис.6).
 |
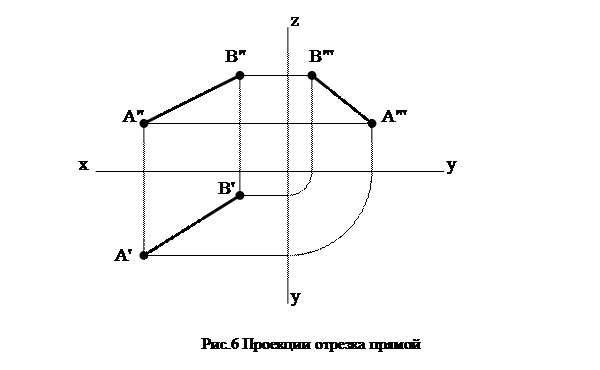

Можно ли утверждать, что этот чертеж выражает именно отрезок прямой? Если через А'В' и А"В" провести проецирующие плоскости 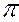 1 и
1 и 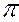 2 соответственно, то в их пересечении получается прямая и её отрезок АВ (рис.7).
2 соответственно, то в их пересечении получается прямая и её отрезок АВ (рис.7).
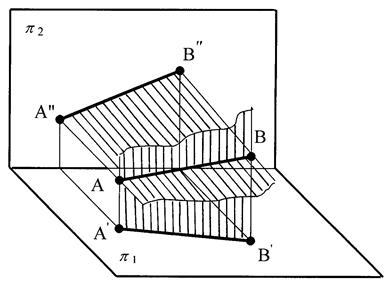
Рис.7 Отрезок прямой АВ и его проекции
Точки А и В находятся на разных расстояниях от плоскостей 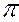 1,
1, 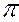 2 и
2 и 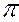 3. Таким образом очевидно, что прямая АВ не параллельна ни одной из плоскостей проекций. При этом её проекции не параллельны и не перпендикулярны ни одной из осей. Такая прямая называется прямой общего положения.
3. Таким образом очевидно, что прямая АВ не параллельна ни одной из плоскостей проекций. При этом её проекции не параллельны и не перпендикулярны ни одной из осей. Такая прямая называется прямой общего положения.
Прямые частного положения
Наряду с прямыми общего положения существуют прямые, расположенные особым образом относительно плоскостей проекций. Их называют прямыми частного положения и подразделяют на следующие виды:
Прямые, параллельные одной из плоскостей проекций:
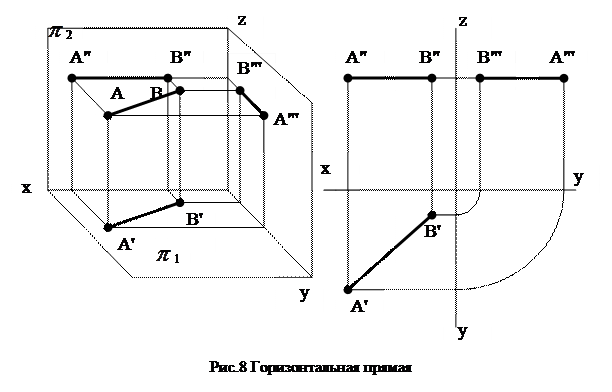
Горизонтальная прямая (рис.8) – это прямая, параллельная горизонтальной плоскости проекций 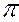 1. Её фронтальная проекция всегда параллельна оси ОХ, а горизонтальная представляет собой натуральную величину отрезка.
1. Её фронтальная проекция всегда параллельна оси ОХ, а горизонтальная представляет собой натуральную величину отрезка.

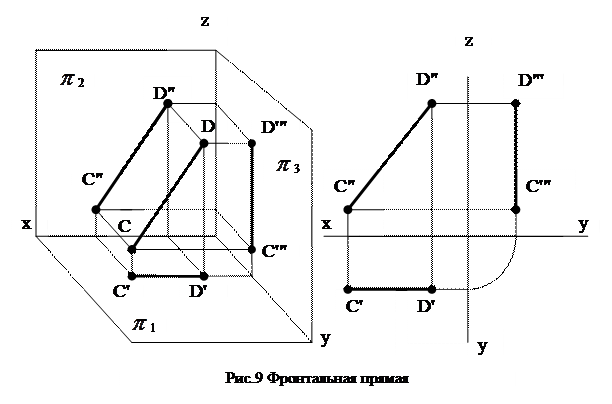
Фронтальная прямая (рис.9) – это прямая, параллельная фронтальной плоскости проекций. Её горизонтальная проекция всегда параллельна оси ОХ, а фронтальная равна натуральной величине заданного отрезка.

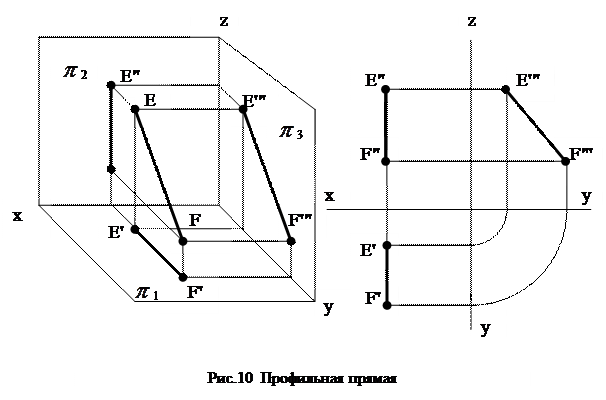
Профильная прямая (рис.10) – это прямая, параллельная профильной плоскости проекций. Её профильная проекция представляет собой натуральную величину, а горизонтальная и фронтальная всегда перпендикулярны оси ОХ.

Прямые, параллельные двум плоскостям проекций:
Горизонтально-проецирующая прямая (рис.11) – это прямая, параллельная фронтальной 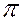 2 и профильной
2 и профильной 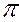 3 плоскостям проекций и перпендикулярная горизонтальной плоскости проекций. При этом на плоскость
3 плоскостям проекций и перпендикулярная горизонтальной плоскости проекций. При этом на плоскость 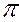 1 она проецируется в точку. Фронтальная и профильная проекции прямой являются натуральной величиной отрезка прямой.
1 она проецируется в точку. Фронтальная и профильная проекции прямой являются натуральной величиной отрезка прямой.
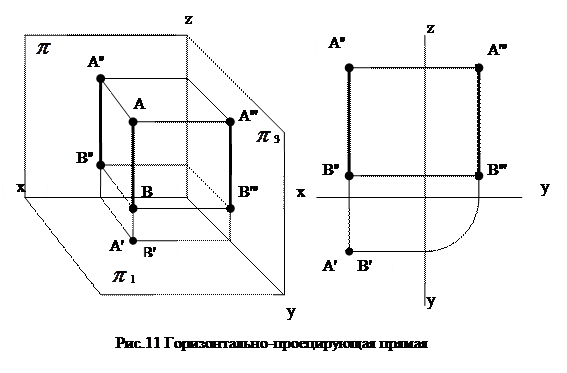

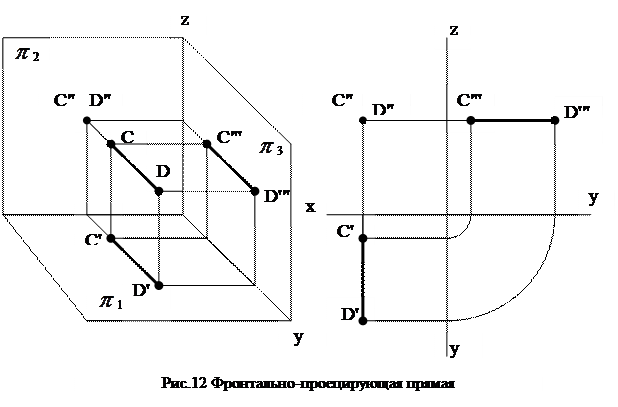
Фронтально-проецирующей прямой (рис.12) называется прямая, параллельная горизонтальной 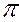 1 и профильной
1 и профильной 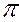 3 плоскостям проекций и перпендикулярная фронтальной плоскости проекций
3 плоскостям проекций и перпендикулярная фронтальной плоскости проекций  2. При этом её горизонтальная и профильная проекции представляют собой натуральную величину отрезка, а фронтальная является точкой.
2. При этом её горизонтальная и профильная проекции представляют собой натуральную величину отрезка, а фронтальная является точкой.

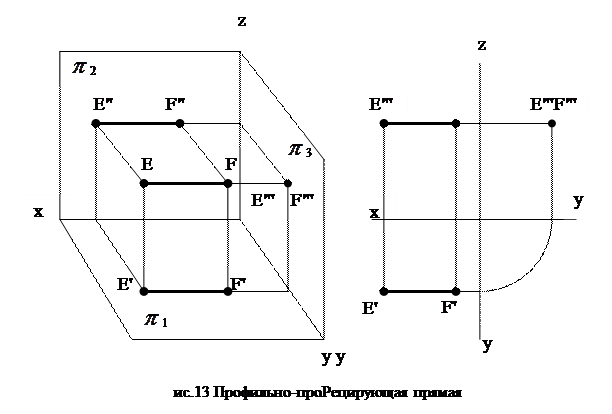
Профильно-проецирующая прямая (рис.13) – это прямая, перпендикулярная профильной плоскости проекций  3 и параллельная горизонтальной
3 и параллельная горизонтальной  1 и фронтальной
1 и фронтальной 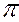 2 плоскостям проекций. При этом на профильную плоскость проекций она проецируется в точку, а на две другие – в свою натуральную величину.
2 плоскостям проекций. При этом на профильную плоскость проекций она проецируется в точку, а на две другие – в свою натуральную величину.
Дата: 2019-03-05, просмотров: 398.