Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

 

Две прямые в пространстве относительно друг друга могут располагаться следующим образом:

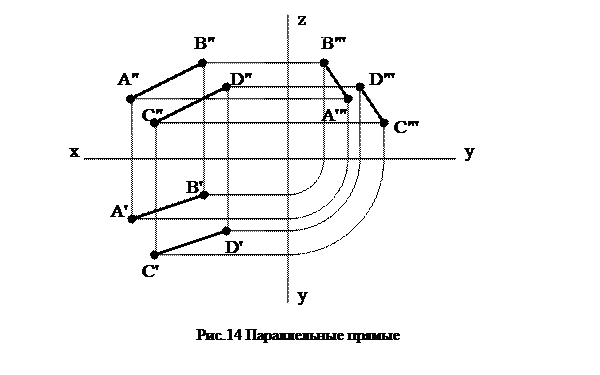
· Быть параллельными друг другу. Если две прямые в пространстве параллельны друг другу, то их одноимённые проекции параллельны между собой (рис.14).

 

 

· Пересекаться. Если две прямые линии пересекаются, то их одноимённые проекции пересекаются в точке (точка 1 на рис.15), которая является проекцией точки пересечения прямых.

 

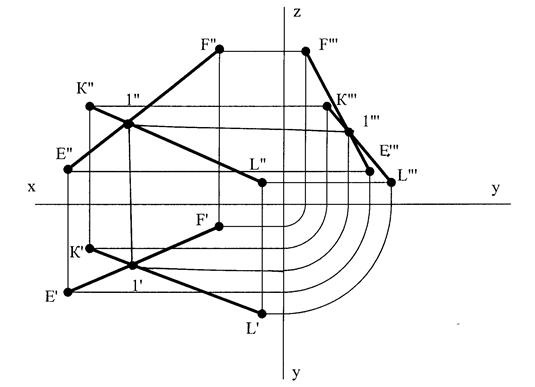
Рис.15 Пересекающиеся прямые

·

 

· Скрещиваться. Скрещивающиеся прямые не параллельны между собой и не пересекаются.

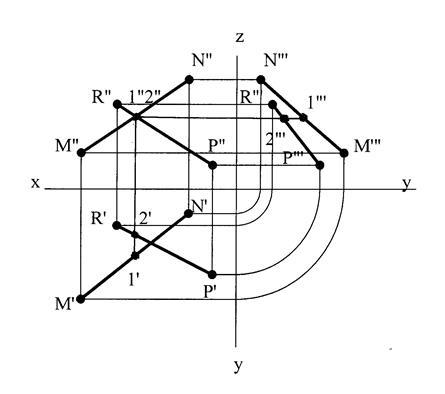
Рис.16 Скрещивающиеся прямые

 

Несмотря на то, что фронтальные проекции проекции скрещивающихся прямых M"N" и Р"R" пересекаются, на самом деле эти прямые не являются пересекающимися. 1 и 2 – это две точки, одна из которых (точка1) лежит на прямой MN, а вторая (точка2) – на прямой РR. Это ясно видно на горизонтальной и профильной проекциях прямых (1'Є M'N',  2'Є Р'R',  1'"Є M"'N"',  2"'Є Р"'R"'). Т.е. эти прямые не пересекаются между собой. Эти прямые также и не параллельны между собой, так как ни одна пара одноименных проекций не параллельна.

 

Следы прямой

Горизонтальным (фронтальным, профильным) следом прямой называется точка пересечения прямой с горизонтальной (фронтальной, профильной) плоскостью проекций (рис.17).

 

 

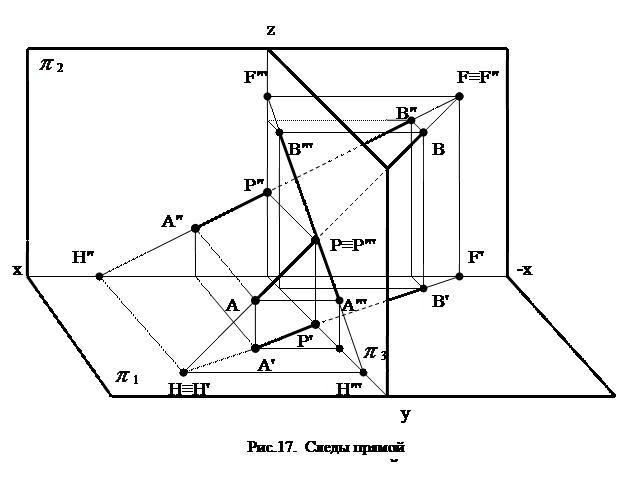
На рис. 17 изображен отрезок прямой общего положения АВ и три его проекции А'В', А"В", А"'В"'. Продолжив отрезок до пересечения с горизонтальной плоскостью проекций 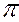₁, получим точку пересечения Н, которая является горизонтальным следом прямой АВ. Как любая точка в системе ортогонального параллельного проецирования, она будет иметь три проекции. Найдем их, помня о том, что точка Н помимо всего прочего лежит на прямой АВ, а, следовательно, каждая её проекция должна находиться на одноимённой проекции прямой. Таким образом получим Н"ЄА"В" и ЄОХ, Н"'ЄА"'В"' и ЄОY. Горизонтальная проекция Н' совпадает с самим следом Н, так как по определению НЄ плоскости 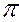₁.

 

 

Аналогичным образом рассуждаем при построении фронтального и профильного следов и их проекций.

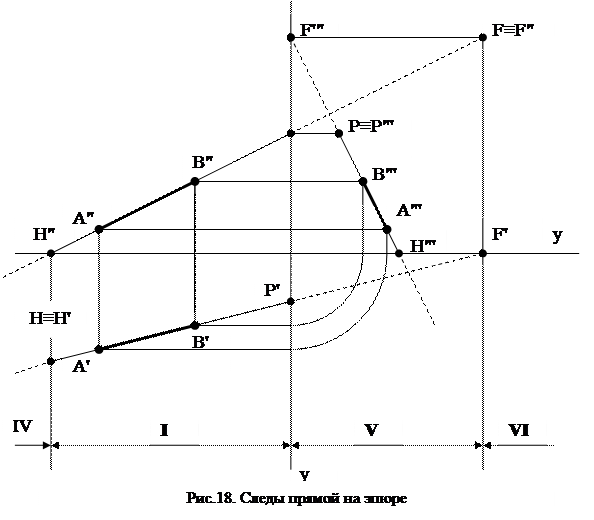
Алгоритм построения следов прямой (рис.18):

1. Находим точку пересечения фронтальной проекции прямой (или её продолжения) с осью Х. В этой точке находится фронтальная проекция горизонтального следа Н".

2. Из точки Н" восстанавливаем перпендикуляр к оси Х до пересечения с горизонтальной проекцией прямой. В точке пересечения получим горизонтальный след прямой Н и его горизонтальную проекцию Н'.

3. Находим точку пересечения горизонтальной проекции прямой с осью Х, получив в этой точке горизонтальную проекцию фронтального следа F'.

4. Из точки F' восстанавливаем перпендикуляр к оси Х до пересечения с фронтальной проекцией прямой. В точке пересечения получаем фронтальный след прямой F и его фронтальную проекцию F".

5. Находим точку пересечения фронтальной проекции прямой с осью Z. В этой точке будет находиться фронтальная проекция профильного следа Р".

6. Из точки Р" восстанавливаем перпендикуляр к оси Z до пересечения с профильной проекцией прямой. В точке пересечения получим профильный след прямой Р и его профильную проекцию Р"'.

7. Находим недостающие проекции следов Н"', F"', Р', помня о том, что это точки, лежащие на прямой АВ, а следовательно каждая их проекция находится на соответствующей проекции прямой.

8. Определяем октанты, через которые проходит прямая и устанавливаем её видимость (прямая считается видимой только в I октанте).

     Прямая общего положения имеет три следа (точки пересечения с каждой из трех плоскостей проекций).

Прямая не будет иметь следа на плоскости проекций в том случае, когда она параллельна этой плоскости. Поэтому прямая может иметь два следа в случае, если она параллельна одной из плоскостей проекций, и один след в том случае, когда она параллельна сразу двум плоскостям проекций, при этом по отношению к третьей она будет располагаться перпендикулярно и проецироваться на нее в точку.

Рассмотрим случай,  когда прямая занимает в пространстве частное положение, например, является профильной прямой, т.е. расположена параллельно профильной плоскости проекций. Такая  прямая будет иметь только горизонтальный и фронтальный следы.

 На рисунке  19 приведено пространственное изображение такой прямой и ее следов:  горизонтального Н и фронтального F, а так же их проекций  (горизонтальная проекция горизонтального следа Н', фронтальная проекция горизонтального следа Н", профильная проекция горизонтального следа Н"', горизонтальная проекция фронтального следа F', фронтальная проекция фронтального следа F", профильная проекция фронтального следа F"').

 

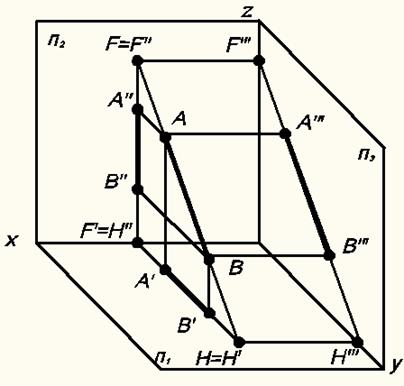
Рис.19. Следы профильной прямой в аксонометрии.

 

   

   На рисунке 20 показано построение следов профильной прямой. Построение начинается с определения профильных проекций следов H''' (горизонтального) и F''' (фронтального). Профильная проекция горизонтального H''' следа находится там, где профильная проекция прямой  А'''B''' пересекает ось y, а профильная проекция фронтального F''' следа находится в пересечении профильной проекции прямой A'''B''' с осью z.  Затем  находим положение остальных проекций следов и самих следов, помня о том, что след прямой это точка,  причем принадлежащая заданной прямой. Поэтому она подчиняется всем законам принадлежности точки заданной прямой, а именно – соответствующая проекция точки лежит на соответствующей проекции прямой по линиям связи (F" Є А"В", Н' Є А'В').

 

 

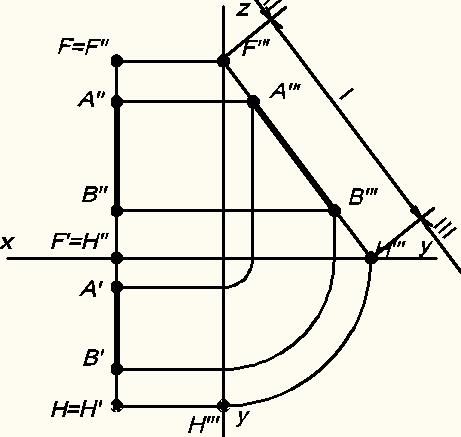
Рис.20. Следы профильной прямой на эпюре.