Как построить прямую, лежащую в плоскости?

Из геометрии знаем, что прямая принадлежит плоскости в том случае, если:

1) она проходит через две точки, принадлежащие данной плоскости;

2) она проходит через одну точку, принадлежащую данной плоскости и параллельна прямой, находящейся в этой плоскости.

Отсюда следует, что в случае задания плоскости следами, прямая принадлежит плоскости, если следы прямой лежат на одноимённых следах плоскости (рис.32 а) и б)). А именно – фронтальный след F прямой m лежит на фронтальном следе плоскости f_{0 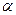,} а горизонтальный след Н прямой m лежит на горизонтальном следе плоскости h_{0 .}

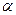Рис.32. Прямая в плоскости, заданной следами:

а) плоскость общего положения; б) плоскость профильно-проецирующая

В случае задания плоскости любым другим способом (см. п.5), необходимо чтобы у прямой с плоскостью было две общие точки. Например, в случае задания плоскости проекциями треугольника АВС (рис. 34), прямая AD имеет с ним две общие точки – это точка А (одна из вершин треугольника) и точка 1, которая лежит на стороне треугольника ВС.

След плоскости – это тоже прямая (по определению) в плоскости.

Поэтому из второго положения о принадлежности прямой плоскости следует, что прямая лежит в плоскости, если она параллельна одному из следов и имеет с другим общую точку (рис.33).

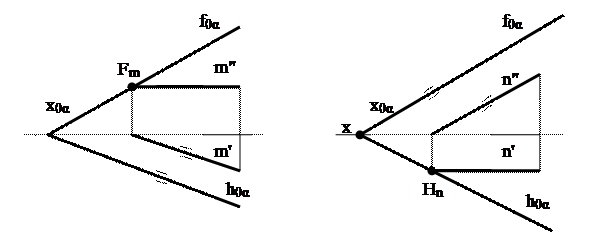
Рис.33. Прямая в плоскости

Чтобы построить точку, принадлежащую плоскости, вначале строят прямую, лежащую в плоскости, а затем на ней берут точку.

Например, задана горизонтальная проекция точки D', надо найти фронтальную проекцию точки D" с условием, что точка D принадлежит плоскости γ, заданной треугольником АВС (рис.34). Строим прямую А'1', проходящую через точку D'. По линиям связи находим фронтальную проекцию прямой А"1", которая определит положение точки D".

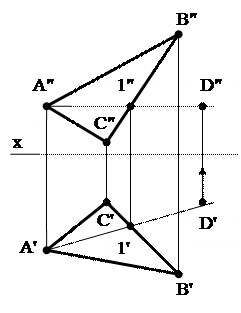
Рис. 34. Прямая и точка в плоскости, заданной треугольником

Если плоскость задана следами, построение выглядит следующим образом (рис.35):

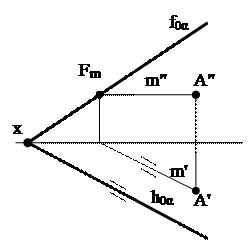
Рис. 35. Точка в плоскости, заданной следами

То есть если задана фронтальная проекция точки A'' и известно, что она лежит в плоскости альфа, то для нахождения горизонтальной проекции точки A' проводим через заданную ее проекцию прямую, принадлежащую плоскости. В данном случае проводим m'' параллельно оси ох, принимаем положение фронтального следа F_m прямой m на фронтальном следе плоскости f_{0 ,} а горизонтальную проекцию прямой m' проводим параллельно горизонтальному следу плоскости h_{0 .} Искомая горизонтальная проекция точки A' будет находится на горизонтальной проекции прямой m' на линии связи.

Линии уровня

К числу прямых, занимающих особое положение в плоскости, относятся горизонтали, фронтали и линии наибольшего наклона к плоскостям проекций, их называют линиями уровня.  Линию наибольшего наклона к плоскости 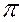₁ называют линией наибольшего ската плоскости  С, её проекции С' и С" (рис. 34).

Горизонтали плоскости h (проекции h' и h") – линии, лежащие в ней и параллельные горизонтальной плоскости проекций 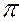₁.

Фронтали плоскости f (проекции f' и f") – линии, лежащие в ней и параллельные фронтальной плоскости проекций 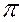₂.

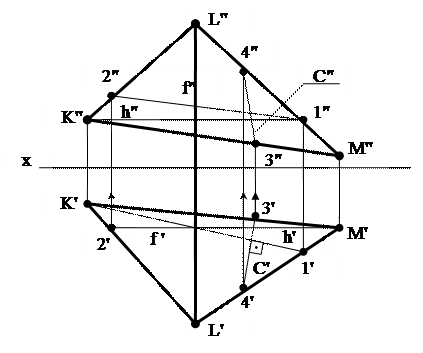
Рис. 34 Линия уровня в плоскости

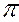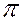Линиями наибольшего наклона плоскости к плоскостям проекций ₁, ₂, 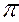₃ называют прямые, лежащие в ней и перпендикулярные к горизонталям, фронталям или профильным прямым плоскости соответственно.

Линия наибольшего ската плоскости – линия, лежащая в плоскости, определяющая угол наибольшего наклона заданной плоскости к горизонтальной плоскости проекций и перпендикулярная к горизонтали. Согласно правилам проецирования прямого угла (теорема о проецировании прямого угла), горизонтальная проекция линии ската перпендикулярна горизонтальной проекции горизонтали.