Начертательная геометрия, как и другие разделы математики, входит в число фундаментальных дисциплин, составляющих основу инженерного образования.

Предметом начертательной геометрии является обоснование методов построения изображений пространственных форм на плоскости и способов решения геометрических задач по заданным изображениям этих форм.

Начертательная геометрия вызывает усиленную работу пространственного воображения, а также передает ряд своих выводов в практику выполнения технических чертежей, обеспечивая их выразительность и точность.

Правила построения изображений в начертательной геометрии основаны на методе проекций.

Рассмотрение метода проекций начинают с построения проекций точки, так как любая пространственная форма рассматривается как ряд точек.

Проекции центральные

При центральном проецировании задаётся плоскость проекций (обозначается строчными буквами греческого алфавита 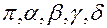 и другими ) и центр проекций – точка (обозначается прописными буквами латинского алфавита – A, B, … S и т.д.), не лежащая в данной плоскости (рис.1.).

Взяв некоторую произвольную точку в пространстве (например (∙) А), проведем через неё и центр проекций S прямую до пересечения с

плоскостью проекций 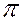₀. Получим А⁰ – проекцию точки А на плоскость 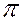₀. Так же  поступим с произвольными точками в пространстве В и С.

В⁰, С⁰  - центральные проекции (∙) В и (∙) С на плоскость 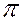₀.

Но в данном случае, имея проекцию точки, нельзя однозначно определить положение самой точки в пространстве, так любая точка, лежащая на проецирующей прямой SA, проецируется в А⁰. Для единственного решения необходимы дополнител 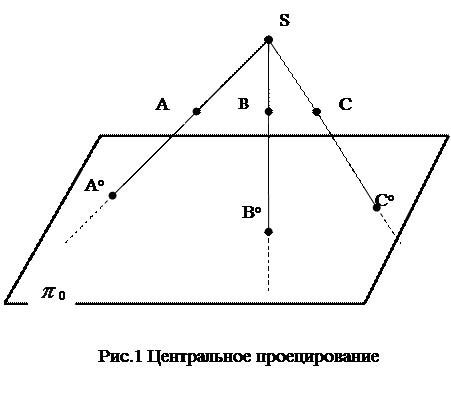ьные условия.

Проекции параллельные

Если принять, что центр проекций бесконечно удалён от плоскости проекций, то проецирующие прямые будут параллельны между собой. Для их проведения должно быть указано некоторое направление (рис.2)

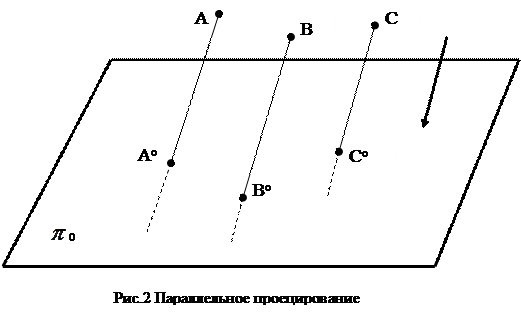Следовательно, параллельной проекцией точки называется точка пересечения проецирующей прямой, проведенной параллельно заданному направлению, с плоскостью проекций.

Существуют правила, распространяющиеся как на центральное проецирование, так и на параллельное:

1. Для прямой линии проецирующей поверхностью в общем случае служит плоскость, потому прямая проецируется в виде прямой;

2. Каждая точка и линия в пространстве имеют единственную свою проекции;

3. Каждая точка на плоскости может быть проекцией множества точек;

4. Каждая линия на плоскости может быть проекцией множества линий;

5. Для построения проекций прямой достаточно спроецировать две её точки;

6. Если прямая параллельна направлению проецирования, то её проекция является точкой;

7. Отрезок прямой, параллельный плоскости проекций, проецируется в натуральную величину.

Метод Монжа

Метод параллельного ортогонального проецирования был развит в трудах французского учёного Монжа.

Гаспар Монж (1746-1818) – крупный геометр и государственный деятель периода правления Наполеона. Его труд по начертательной геометрии долго не публиковался, так как имел большое практическое значение для выполнения чертежей военных объектов, и увидел свет только в конце 18 века. Изложенный Монжем метод параллельного ортогонального (т.е., прямоугольного) проецирования до сих пор остается основным методом составления технических чертежей, обеспечивая выразительность, точность и удобоизмеримость предметов на плоскости.