Будь-яку ST-систему легко можна перетворити в ізоморфну систему з поведінкою. Щоб показати, як це робиться, візьмемо довільну ST-систему

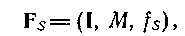 (4.76)

де М, зрозуміло, компактна маска. Припустимо, що будь-який наступний стан відповідає більшому значенню параметра, чим передування.

Розглянемо тепер систему з поведінкою

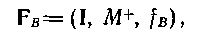 (4.77)

гдеопределяєтся через М таким чином:

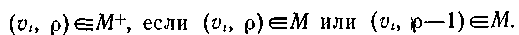 (4.78)

Тоді для будь-якого набору даних із загальної представляючої системи I всі вибірки даних, що дають одну пару станів для маски М, скажемо пару, дають і один і той же стан для маски, скажемо стан с+. Якщо дані повністю вибираються за допомогою обох масок, то частоти і повинні бути однакові. Отже

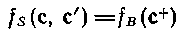(4.79)

де стан складається із з і породжуваної частини, назвемо її. Таким чином, функція поведінки еквівалентна ST-функції при однозначній відповідності

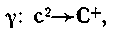 (4.80)

де тоді і тільки тоді, коли .

Маску (4.78) називатимемо розширеною маскою М. Она визначена в припущенні, що стани породжуються у порядку зростання параметра. При зворотному порядку альтернативна розширена маска, скажемо маска, визначається трохи інакше:

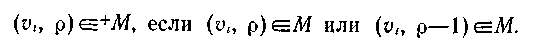 (4.79)

Можна аналогічно тому, як це було показано для М+, показати, що система з поведінкою

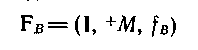
ізоморфна ST-системі, визначеній для тієї ж представляючої системи I і маски М.

Відповідність між масками М, і масками М, показана відповідно на мал. 4.11а і б. На малюнку також показано однозначну відповідність і його аналог для маски і

Для заданої системи з поведінкою

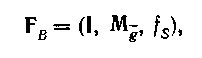 (4.81)

Ізоморфна ST-система при тій же представляючій системі I існує тільки тоді, коли М - компактна маска і для будь-якої підмаски . Якщо ці умови виконані, то зрозуміло, що ST-система 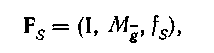(4.82)

де - породжувана частина (згідно певному порядку породження), яка ізоморфна при відповідній однозначній відповідності між безліччю станів З (заснованому на М) і (заснованому ). Дане перетворення з системи з поведінкою в ізоморфну ST-систему для одного з порядків породження показано на мал. 4.11,в.

Для направлених систем змінюючими стан аналогами функцій поведінки будуть відповідно наступні ST-функції:

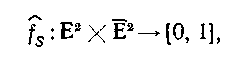 (4.83)

де Е має той же сенс, що і для систем з поведінкою, і - умовна вірогідність, сенс якої однозначно визначається її загальноприйнятим позначенням

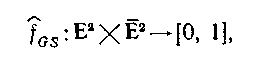 (4.84)

де - що породжують умовну вірогідність;

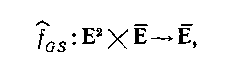 (4.85)

де.

Змінюючими стани аналогами для направлених систем з поведінкою будуть відповідно направлена ST-система

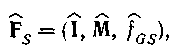 (4.86)

і направлена ST-система, що породжує

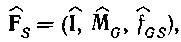 (4.87)

де і визначаються так само, як і для систем з поведінкою.

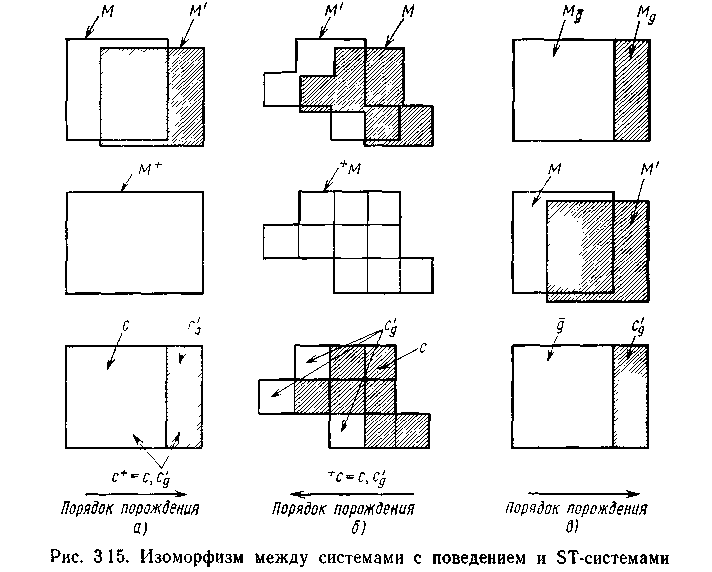
Мал. 4.11. Ізоморфізм між системами з поведінкою і ST-системами

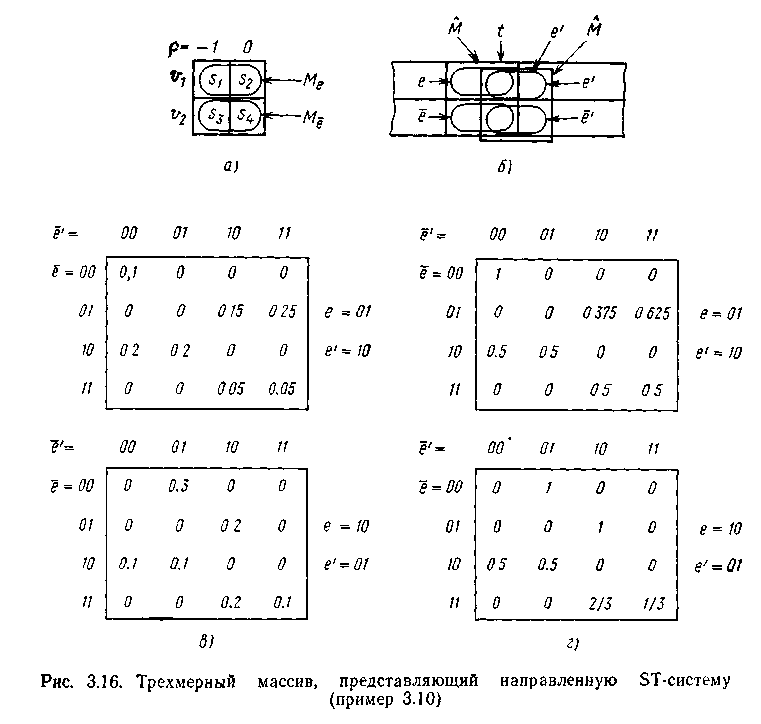
Мал. 4.12. Тривимірний масив, що представляє направлену ST-систему

Функції (4.83) і (4.84) зручно представляти у вигляді масивів квадратних матриць (тривимірних масивів) по одній матриці для кожної умови . Зручні також діаграми, подібні діаграмам для нейтральних ST-систем. Для направлених систем зв'язку на діаграмах позначаються не тільки значеннями відповідної ST-функції, але і умовами . Функції (4.85) можна представляти у вигляді матриць, рядки яких відповідають станам е, стовпці - станам, а елементами є відповідні стани . Ці функції представляються також у вигляді діаграм, таблиць і в деяких випадках за допомогою формул, алгебри. з

Приклад 4.6. На мал. 4.12 приведена проста направлена ST-система (без інтерпретації). Її представляюча система складається з вхідної змінної і вихідної змінної, кожна має два стани 0 і 1. Маска системи М показана на мал. 4.12,а, а на мал. 4.12,б приведені відповідні компоненти станів, породжені двома її послідовними положеннями на матриці даних. На мал. 4.12,в і г показані відповідно функції і у вигляді тривимірних масивів. У даному прикладі масив складається з двох матриць.

К.Р. № 16

Приведіть приклад переходу від деякої ST-системи до ізоморфоной системи з поведінкою.

Лекція 17

Види систем, що породжують

системи з поведінкою

1. базовиє-

а. рівняння (4.12) -нейтральные;

b. рівняння (4.28) -направленные;

2. що породжують:

а. рівняння (4.19) -нейтральные;

b. рівняння (4.32) -направленные;

ST-системи

1. базові:

а. рівняння (4.66) -нейтральные

b. рівняння (3.93) -направленные;

2. що породжують:

а. рівняння (4.86) - нейтральні;

b. рівняння (4.87) -направленные.

Як було показано, будь-яка ST-система може бути перетворена в ізоморфну систему з поведінкою, тоді як зворотне перетворення можливо тільки при певному типі масок. Отже, системи з поведінкою більш загальні, ніж ST-системи.

Два основні недоліки ST-систем очевидні: обмеженість із-за використання тільки компактних масок і власна надмірність, що виникає з накладення поточного і наступного станів.

ST-системи, коли вони застосовні, представляють для дослідників певні переваги. Мабуть, ST-функції зрозуміліше людині, чим аналогічні функції поведінки.

Для систем, що породжують, виділені різні відмінності. Це відмінності, виділені для систем нижчих рівнів, і деякі нові. Серед перших найбільш істотними є:

1. впорядкованість параметричної множини, що дозволяє ввести важливе поняття маски;

2. впорядкованість безлічі станів, що грає істотну роль в спрощенні процедур для систем, що породжують, і при роботі з не повністю певними наборами даних;

3. відмінність чітких і нечітких каналів спостереження, що дають відповідно чіткі або нечіткі дані і вимагаючих застосування різних методів обробки даних;

4. відмінність між нейтральними і направленими системами, з якими слід поводитися по-різному.

Відмінностями, що відносяться до систем, що породжують, але не до систем даних і початкових систем, є:

1. детермінована і недетермінована систем;

2. по використовуваній масці розрізняються системи без пам'яті і системи, що породжують, залежні від минулого.

Зрозуміло, ці методологічні відмінності характеризують і системи вищих рівнів.